基于室内试验的土壤入渗深度动态模拟研究

姚丽，王仰仁，通信作者，战国隆，牛少卿

基于室内试验的土壤入渗深度动态模拟研究

姚丽1,2，王仰仁1,2，通信作者，战国隆3，牛少卿3

（1. 天津农学院 水利工程学院，天津 300384；2. 天津市节水灌溉技术与装备校企协同创新实验室，天津 300384；3. 大禹节水（天津）股份有限公司，天津 301712）

入渗是土壤水分运动的基本特性，是降雨产流、侵蚀、非点源污染等过程研究的重要依据，快速准确地测定和计算土壤入渗速率及其入渗深度具有重要意义。在天津市武清区北靳庄村和天津农学院西校区试验田选取土样，进行室内积水（积水深度为5 cm）入渗试验，依据测得的土壤水入渗数据，利用Philip、Horton和kostiakov-Lewis 3个模型进行累计入渗量的拟合；在此基础上以累计入渗量为自变量进行了入渗深度的动态模拟，并对入渗深度的理论模型和线性经验模型的拟合效果进行了比较。结果表明：不同质地、不同结构的土壤有其相应适用的模型；入渗深度模拟以基于Horton入渗模型的理论公式更适用；与常规风干含水率土壤制备土柱相比，采用含水率高的土壤制备入渗试验土柱，可显著减小土壤的入渗速率。

土壤入渗；入渗深度；霍顿模型；剖面含水率

入渗是土壤水分运动的基本特性，是降雨产流、侵蚀、非点源污染等过程研究的重要依据，快速、准确地测定和计算土壤入渗速率及其入渗深度具有重要意义[1]，国内外学者对此进行了广泛研究。Bodman等研究表明，土壤含水率对入渗过程的影响只存在于初期阶段，表现为入渗速率随含水率的增大而不断减小，并且随着入渗的进行，这种影响越来越小，以至于可以忽略不计[2]。李贵玉以延安燕沟流域为试验基地，阐述了不同土地利用类型之间土壤入渗性能的差异[3]。Schwankl等研究了在沟灌条件下土壤的入渗性能，认为可以采用在较短时间内的入渗过程预测较长时间的土壤入渗信息[4]。徐海芳采用经典统计分析法对禹城综合实验站的土壤参数（稳定入渗率与入渗经验指数）的空间变异程度进行了分析研究[5]。夏江宝等总结了不同林地、草地、地形地貌、土地利用方式等外界条件对土壤入渗性能的影响，得出了不同外界条件下土壤入渗的变化规律[6]。

对于入渗深度的模拟和预测，可以采用更具机理性的垂直一维土壤水分运动动力学模型[7]，但该方法运算耗时、复杂，在生产实际中更多地采用经验型入渗模型。郭忠升等在对人工林地剖面土壤水分的长期定位观测和对长时间序列定位观测资料分析的基础上，提出了自然条件下土壤水分入渗深度和入渗量的简易确定方法[8]；陈海波等以华南地区的3种土壤为试验材料进行了喷灌入渗试验，利用神经网络建立了土壤入渗类别识别模型，将试验数据回归建立了灌溉水在各类土壤中的入渗预测模型，并对模型进行了室内试验验证，得出入渗深度模型的预测深度与测试的入渗深度的误差不超过20%[9]；管宪伟等基于入渗流量平衡，发现入渗深度和渗透系数成正比、与土壤干密度和孔隙率成反比，据此提出了估算降雨条件下边坡入渗深度的计算公式[10]。从以上研究中可以看出，对于入渗量的研究较多，对于入渗深度的研究相对较少。据此，笔者根据实际测得的土壤水入渗数据，进行入渗深度的动态模拟研究。

1 材料与方法

1.1 供试土样

试验于天津市武清区北靳庄试验区（117°1′E，39°22′N，海拔8 m）和天津农学院西校区农田水循环试验基地（116°57′E，39°08′N，海拔5.49 m）进行，试验区均属暖温带半湿润大陆性季风气候。北靳庄试验区：年平均气温为11.6 ℃，1月平均气温为-5.1 ℃，7月平均气温为26.1 ℃，年平均降水量为606 mm，土壤为中壤土，土质疏松肥沃，适宜农业生产，地下水埋深变幅在0.5～4.6 m之间。天津农学院西校区（粉砂壤土）农田水循环试验基地：试验区总面积为1 hm2，地下水埋深变幅在2.06～3.70 m之间。

在两个试验区选取具有代表性的地块，从表层至50 cm深处依次取土，取样方向均为垂直，将土样带回实验室去草、风干、过筛（2 mm），测定风干土壤含水率，试点分层土壤水分特征参数拟合值如表1所示（测试方法为离心机法（R11D2））。

表1 试点分层土壤水分特征参数拟合值表

试点 土层深度土壤水分特征曲线参数优化拟合值 cmcm3∙cm-3cm3∙cm-3 天津市武清区北靳庄试验田0～200.369 70.033 00.020 61.115 8 20～400.364 90.045 20.014 61.155 1 40～600.358 00.031 00.051 01.161 7 60～800.395 30.046 00.011 01.182 9 天津农学院试验田0～300.391 00.023 00.052 41.169 0 30～1000.505 00.074 00.052 01.541 0 100～1300.473 00.079 00.014 91.251 0

1.2 试验装置与测试方案

试验在天津农学院水力学实验室进行，采用扰动土进行室内土柱入渗试验。试验设备主要包括透明有机玻璃筒、基座、导水管，有机玻璃筒内径10 cm，高60 cm，基座高7 cm，利用导水管向外排水，试验装置如图1。

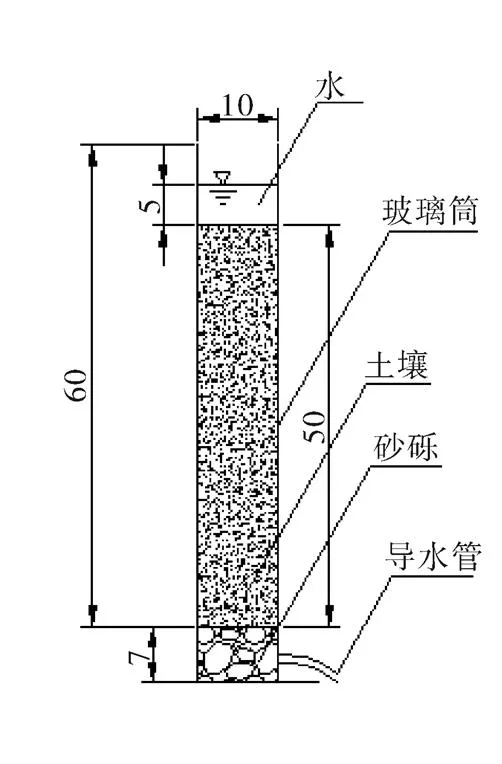
图1 入渗试验装置图（单位：cm）

同步进行4组试验，为确保试验的准确性，每组设置重复试验，首先向基座内加入砂砾，保证土壤的均匀下渗，便于排水，将准备好的3个渗透筒与基座粘合。第一组试验设置3个重复，相应土柱编号为1、2、3，土柱高度50 cm，装填土壤容重为1.3 g/cm3，风干含水率为2.58%，分5层填土，每层10 cm，土重1 046.83 g；第二组、第三组、第四组试验均设2个重复，相应土柱编号为4和5、6和7、8和9，土柱高度均为40 cm，装填土壤容重为1.35 g/cm3。第二组试验土柱含水率上下一致，均为1.52%，分8层填土，每层5 cm，土重538.36 g；第三组试验，土柱的上半部分土壤含水率为1.52%，分4层填土，每层5 cm，土重538.36 g，土柱下半部分的土壤含水率为10%，分4层填土，每层5 cm，土重583.16 g；第四组试验，土柱上半部分土壤含水率为10%，分4层填土，每层5 cm，土重583.16 g，土柱下半部分土壤含水率为10%，分4层填土，每层5 cm，土重538.36 g。土柱基本情况如表2所示。

试验过程中用秒表定时，观测水位的变化，始终保持水层高度在4～5 cm之间，当水层高度下降到4 cm时，及时加水，使水层高度达到5 cm。观测土柱湿润锋变化情况，测量入渗深度时，沿土柱横断面十字方向选取4个测试点，记录深度值，当相邻两次加水时间相等时，入渗试验结束。

表2 试验土柱基本情况

试验组土柱编号土柱高度/cm容重/g∙cm-3含水率/%每层加土重/g加土层数 一1、2、3501.32.581 046.835 二4、5401.351.52538.368 三6、7401.351.52（上20 cm）10.00（下20 cm）538.36583.1644 四8、9401.3510.00（上20 cm）1.52（下20 cm）583.16538.3644

1.3 入渗模型

入渗深度随时间的变化过程主要有两种描述方法，一种是基于Green-Ampt模型累计入渗量的入渗深度理论公式，第二种是基于累计入渗量的经验线性公式，见表3。

表3 入渗量及入渗深度模型

项目模型公式 入渗深度理论公式 经验公式 累计入渗量Philip Horton kostiakov-Lewis

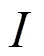
其中累计入渗量可以采用多种公式进行模拟，有理论的或经验的入渗公式。理论公式主要包括Green-Ampt公式[11]、Philip公式、Smith公式和Parlange公式等，经验公式主要包括kostiakov、Horton公式、Holtan公式、kostiakov-Lewis[12]等。本文选取Philip公式和Horton公式和kostiakov- Lewis公式（表3），分析累积渗入量与时间的关系，并在此基础上进行入渗深度的动态模拟。

表3各式中参数采用最小二乘法拟合确定，其目标函数（公式（1））为公式计算值与观测值误差的平方和最小。

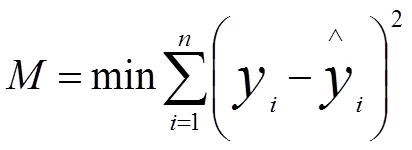
2 结果与分析

2.1 累计入渗量的拟合结果分析

利用Philip、Horton、kostiakov-Lewis 3个模型对实测数据进行拟合，拟合结果见表4。从每组试验中选取有代表性的土柱（第一组选3号土柱，第二组选5号土柱，第三组选6号土柱，第四组选8号土柱），结合实测数据，给出累计入渗量的拟合曲线，见图2。

表4 3种入渗模型参数拟合结果

入渗模型土柱编号 123456789 PhilipS5.3678.3623.5458.98510.1179.85110.4720.6860.829 A0.0620.1090.081-0.098-0.089-0.096-0.1020.0120.013 R 20.999 20.998 20.998 10.983 70.974 10.983 40.974 50.985 10.983 1 R 2平均0.998 50.978 90.979 00.984 1 Horton/cm∙min-10.1640.3140.1290.0190.0260.0290.0310.0180.021 /cm∙min-10.8401.6470.4171.4211.6491.8582.25810.5344.748 β0.009 80.015 90.004 40.009 90.008 80.011 40.013 00.587 90.225 1 R 20.997 40.998 10.997 50.977 80.984 00.971 20.980 30.995 10.991 7 R 2平均0.997 70.980 90.975 80.993 4 kostiakov-LewisK3.9025.4012.55514.44423.48621.74923.79412.77513.535 α0.5850.4980.5780.4020.3390.3450.3990.0490.065 /cm∙min-10.009 40.259 70.054 5-0.053 6-0.026 9-0.031 0-0.031 00.017 00.020 0 R 20.999 50.990 60.99 830.992 50.991 40.997 40.992 80.993 90.990 4 R 2平均0.996 10.992 00.99510.992 2

由表4可以看出，对于第一组试验（1号、2号、3号），3个模型的复相关系数（2）均在0.9以上，其中Philip模型的2最大，Horton模型的2适中，kostiakov-Lewis模型的2最小，可以看出对于北靳庄试点的土壤来说，Philip模型的累计入渗量拟合效果最好；对于西校试验田的土壤，第二、三组Philip模型、kostiakov-Lewis拟合参数稳渗率出现负值，不符合物理意义，3个模型的2均在0.9以上，差异较小，以Horton模型的累计入渗量拟合效果最好。

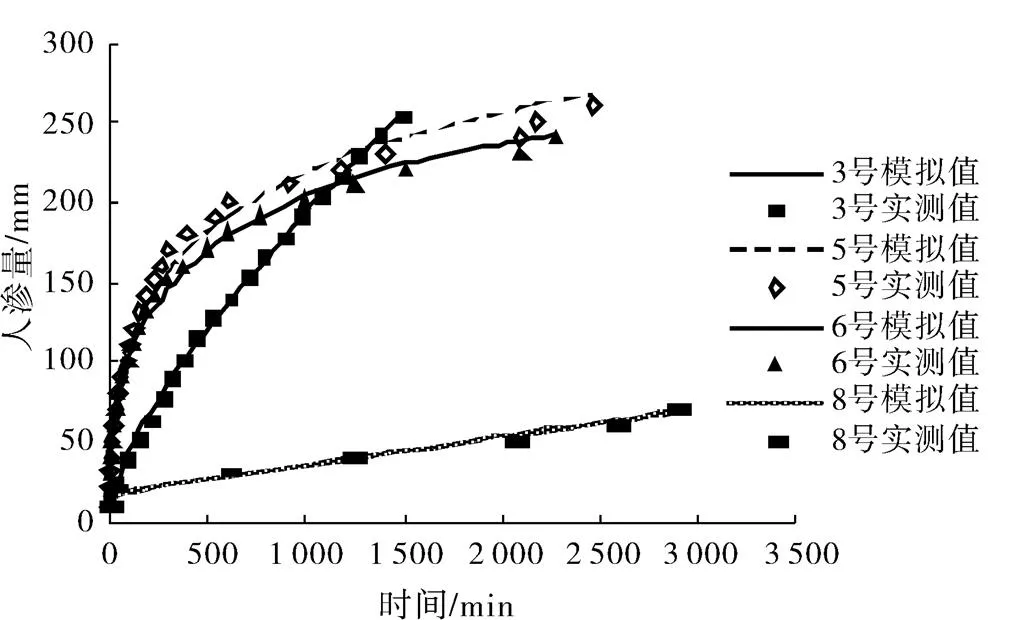
图2 累计入渗量随时间的变化过程（Horton）

从图2可以看出，在相同时间内，第四组试验（8号土柱）的累计入渗量明显小于第一、二、三组试验土柱的入渗量；与第二组（5号土柱）和第三组（6号土柱）曲线比较，第一组试验（3号土柱）更早的达到稳渗，在1 400 min前，累计入渗量小于5号、6号土柱，1 400 min后，累计入渗量明显大于5号、6号土柱；5号、6号土柱的拟合曲线变化趋势较为接近，二者的入渗规律相近。说明第四组试验（上湿下干）土柱的制备，会明显改变土壤的入渗特性；不同质地、不同结构的土壤具有不同的入渗规律。

2.2 入渗深度的模拟分析

在上述入渗模型参数的基础上，建立入渗深度随时间的变化关系，根据入渗深度测试数据，拟合得到入渗深度模型的参数，如表5（理论模型）和表6（经验模型）所示，相应的入渗深度拟合曲线见图3（选取土柱同上）。

表5 入渗深度理论模型参数拟合结果

土柱编号PhilipHortonkostiakov-Lewis 10.390 50.998 00.390 00.996 60.392 20.998 6 20.399 90.994 90.404 10.986 80.371 20.995 1 30.399 60.998 20.402 40.994 70.400 80.998 0 平均值0.396 70.997 00.398 80.992 70.388 10.997 2 Cv0.013 50.001 90.003 00.005 60.053 90.002 1 40.356 30.997 20.393 00.986 00.372 10.999 2 50.360 70.993 70.434 30.979 30.409 90.988 3 平均值0.358 50.995 50.413 70.982 70.391 00.993 8 Cv0.008 70.002 50.070 60.004 80.068 40.007 8 60.384 90.977 00.463 70.939 20.366 30.964 7 70.306 90.986 20.384 50.983 60.417 70.989 8 平均值0.345 90.981 60.424 10.961 40.392 00.977 3 Cv0.159 50.006 60.132 10.032 70.127 60.018 2 80.369 10.963 80.365 90.970 70.366 30.960 7 90.413 90.933 90.408 20.952 40.417 70.955 3 平均值0.391 50.948 90.387 10.961 60.392 00.958 0 Cv0.08090.022 30.077 30.013 50.092 70.004 0

由图3可以看出，图3的拟合曲线变化趋势与图2一致，在同样入渗时间条件下，8号土柱的入渗深度显著小于其他3个土柱的入渗深度，表明试验土柱上半剖面含水率较大，会显著减小土壤入渗速率和入渗数量（包括累计入适量和入渗深度）；第二组试验（3号土柱）与第三组试验（5号土柱）入渗深度接近；第一组试验土柱入渗深度接近500 mm，第二、三、四组试验土柱入渗深度接近400 mm，这与试验玻璃筒的高度有关。

图3 入渗深度随时间的变化过程（Horton）

由表5和表6可以看出，同一土柱入渗深度理论模型和经验模型的复相关系数相等，表明两者的拟合精度相同。另外，从参数的稳定性来看，参数的变化比较稳定，变化范围为1.77～3.73之间，其变异系数变化范围在0.037 6～0.225 6之间；参数的变化幅度较大，其变异系数变化范围为-14.086 0～2.048 5，参数的值甚至出现负值，也就是说当入渗量为0时，入渗深度为负值，这不符合物理意义，因而入渗深度的理论模型明显好于经验模型。

表6 入渗深度经验模型参数拟合结果

土柱编号PhilipHortonkostiakov-Levis ndR 2ndR 2ndR 2 12.5623.850.998 02.5030.610.996 62.5029.990.998 6 22.76-11.860.994 92.64-0.180.986 82.6829.140.995 1 32.5615.310.998 22.4526.820.994 72.5219.000.998 0 平均值2.629.100.997 02.5319.090.992 72.5726.050.997 2 Cv0.043 22.048 50.001 90.038 90.879 70.005 20.03760.234 90.001 9 42.7715.170.997 22.1454.110.986 02.97-15.920.999 2 52.5040.590.993 71.7750.510.979 32.63-10.680.988 3 平均值2.6327.880.995 51.9652.310.982 72.80-13.300.993 8 Cv0.072 20.644 70.002 50.134 00.048 70.004 80.086 5-0.278 60.007 8 62.5910.500.977 01.8446.420.939 22.73-36.970.964 7 73.58-12.840.986 22.3937.260.983 63.74-85.380.989 8 平均值3.08-1.170.981 62.1141.840.961 43.24-61.180.977 3 Cv0.225 6-14.086 00.006 60.182 00.154 70.032 70.219 0-0.559 50.018 2 83.2038.110.963 83.732.530.970 73.703.630.960 7 92.5353.540.933 92.9819.970.952 42.7230.410.955 3 平均值2.8645.830.948 93.3511.250.961 63.2117.020.958 0 Cv0.165 70.238 10.022 30.156 11.095 80.013 50.215 31.112 40.004 0

3 讨论

关于农田土壤入渗动态模拟精度，周鑫洋等通过对天津农学院西校区试验田非扰动土进行入渗试验，得出Horton模型适应性较好[13]；范严伟等对陕西杨凌农田土壤进行试验研究，得出Philip模型的适应性较好[14]；本研究所选土壤最适宜的入渗模型为Horton模型。表明不同的土壤适应的模型不同，主要原因是不同土壤的质地、结构有较大差异。范严伟等认为初始含水率越高，土壤入渗能力越小[14]；聂卫波等采用陕西杨凌地区的土壤进行入渗试验，得出在相同初始条件下累计入渗量随初始含水量的增大而减小的结论[15]，这与本研究结果一致；任长江等对妫水河流域平原区未受干扰的表层以下1 m土层的亲水性土壤和山区表层斥水性土壤进行入渗机理试验，得出初始含水率越高，相同时间内入渗量越大的结论[16]。这与传统的初始含水率越高，基质吸力越小，入渗率越小的观念相矛盾。对该结果的解释，任长江等认为土壤团聚体的快速湿润会产生致使团聚体破碎的崩解力，土壤含水率越低团聚体崩解对透水孔隙结构的堵塞和挤压越强，渗透能力降低幅度越大，由于土壤含水率增大，土壤黏聚力和内摩擦角都随之减小，团聚体破碎程度也越小，团聚体越多、水稳性团聚体平均直径越大，因而水分入渗也越快[16]。

对于土壤入渗深度的动态模拟，主要有两种模型，一种是理论模型，另一种是经验线性模型，二者的拟合精度一致，但线性经验模型参数的稳定性较差，尤其常数项变异较大。范文涛等和刘春成等均采用不同土壤进行了室内扰动土入渗试验，认为累计入渗量和水平湿润锋呈良好的线性关系[17-18]。刘春成等建立的线性表达式中参数的变异系数为0.23，本文中线性公式参数的变异系数的变化范围为0.037 6～0.225 6，二者较为接近，参数也出现负值，拟合精度均较高，与本研究结果一致，应选择理论模型更为合适。

4 结论

（1）不同质地、不同结构的土壤有相适应的模型，对于累计入渗量，北靳庄土壤适宜的模型是Philip，天津农学院西校区土壤适宜的模型是Horton模型。

（2）入渗深度的模拟宜选择理论模型，其中Horton模型的拟合精度最高，稳定性最好。

（3）与常规风干含水率土壤制备的土柱相比，采用含水率高的土壤制备入渗试验土柱，会显著减小土壤入渗速率。

[1] 朱良君，张光辉，任宗萍. 4种土壤入渗测定方法的比较[J]. 水土保持通报，2012，32（6）：163-167.

[2] Bodman G B，Colman E A. Moisture and energy conditions during downward entry of water into soils[J]. Soil Science Society of America Journal，1944，8（8）：116.

[3] 李贵玉. 黄土丘陵区不同土地利用类型下土壤入渗性能对比研究[D]. 杨凌：西北农林科技大学，2007.

[4] Schwankl L J，Raghuwanshi N S，Wallender W W. Time series modeling for predicting spatially variable infi- ltration[J]. Journal of Irrigation and Drainage Engineering，2000，126（5）：283-287 .

[5] 徐海芳. 农田土壤入渗参数的空间统计特征[D]. 西安：长安大学，2005.

[6] 夏江宝，杨吉华，李红云. 不同外界条件下土壤入渗性能的研究[J]. 水土保持研究，2004，11（2）：115-117.

[7] 王仰仁，李炎，金建华，等. 反演法确定田间尺度水分运动参数的研究[J]. 天津农学院学报，2013，20（1）：1-6.

[8] 郭忠升，邵明安. 半干旱区人工林地土壤入渗过程分析[J].土壤学报，2009，46（5）：953-958.

[9] 陈海波，胡月明，胡均万，等. 基于神经网络的灌溉水入渗深度预测模型研究[J]. 华南农业大学学报，2009，30（3）：99-102.

[10] 管宪伟，钱财富. 降雨条件下土质边坡入渗深度的估算[J]. 治淮，2015（7）：18-19.

[11] 雷志栋，杨诗秀，谢森传. 土壤水动力学[M]. 北京：清华大学出版社，1988．

[12] 李元华，罗金耀. 节水灌溉理论与技术[M]. 武汉：武汉大学出版社，2003.

[13] 周鑫洋，王仰仁，刘群昌. 四个入渗公式对农田潮土的适应性研究[J]. 灌溉排水学报，2015，34（8）：96-100.

[14] 范严伟，赵文举，王昱. 初始含水率对垂直一维入渗Philip模型参数的影响[J]. 兰州理工大学学报，2014，40（5）：60-64.

[15] 聂卫波，马孝义，王术礼. 一维土壤入渗特性数值模拟[J]. 灌溉排水学报，2009，28（3）：53-57.

[16] 任长江，赵勇，王建华，等. 斥水性土壤水分入渗试验和模型[J]. 水科学进展，2018，19（6）：839-847.

[17] 范文涛，牛文全，张振华，等. Philip模型与修正的Green-Ampt模型互推参数的特性分析[J]. 灌溉排水学报，2012，31（2）：73-77.

[18] 刘春成，李毅，任鑫，等. 四种入渗模型对斥水土壤入渗规律的适用性[J]. 农业工程学报，2011，27（5）：62-67.

Dynamic simulation of soil infiltration depth in farmland based on laboratory experiments

YAO Li1,2, WANG Yang-ren1,2,Corresponding Author, ZHAN Guo-long3, NIU Shao-qing3

（1. College of Water Conservancy Engineering, Tianjin Agricultural University, Tianjin 300384, China; 2. Tianjin City Water Saving Irrigation Technology and Equipment School and Enterprise Collaborative Innovation Key Laboratory, Tianjin 300384, China; 3. Dayu Water Saving（Tianjin）Co. Ltd., Tianjin 301712, China）

Infiltration is the basic characteristics of soil water movement, and it is an important basis for the study of rainfall runoff, erosion, non-point source pollution, etc. It is of great significance to quickly and accurately determine and calculate soil infiltration rate and its infiltration depth. In this paper, soil samples were taken from the Beijinzhuang experimental field in Wuqing District, Tianjin. The infiltration test was carried out indoors（water depth: 5 cm）. Based on the measured soil water infiltration data, the three models, Philip, Horton and kostiakov-Lewis, were used to fit the cumulative infiltration amount. On this basis, with the cumulative infiltration amount as the independent variable, the infiltration depth was simulated, and the fitting effects of the theoretical model and the linear empirical model were compared. The results showed that different soils have different models; the theoretical formula based on the Horton infiltration model is more suitable for the infiltration depth simulation; compared with the conventional air-dried soil with high moisture content, the infiltration test soil column prepared by using the soil with high moisture content significantly reduces the soil infiltration rate.

soil infiltration; infiltration depth; Horton model; section moisture content

1008-5394（2019）04-0083-06

10.19640/j.cnki.jtau.2019.04.017

S275

A

2019-01-17

天津市重点科技支撑项目（17YFZCSF00930）；天津市节水灌溉技术与装备校企协同创新重点实验室（17PTSYJC00110）；天津市农业科技成果转化与推广项目（201701150）。

姚丽（1994-）女，硕士在读，研究方向为水资源的高效利用。E-mail：lilili320yao@163.com。

王仰仁（1962-），男，教授，博士，现主要从事灌溉排水技术教学与科研等工作。E-mail：Wyrf@163.com。

责任编辑：宗淑萍