一种自制环氧树脂结构胶粘剂的动态黏弹性能研究
胡东岚,李 卉,罗迎社,江大志
(1.中南林业科技大学 a.工程流变学湖南省重点实验室;b.土木工程与力学学院,湖南 长沙 410004;2.国防科技大学 空天科学学院,湖南 长沙 410073)
结构物在其制造过程中就有微裂缝存在,在使用过程中随环境、外力的影响,会产生新的裂缝或使原有裂缝扩展。20世纪50年代初,人们开始使用聚合物修补结构物裂缝[1]。随着新的聚合物的出现,以及在实践中发现了环氧树脂胶粘剂具有许多结构物裂缝修补所需的优良性能,环氧胶粘剂在该领域中的使用急剧增长,不仅为工程修补节省了大量资金,而且加快了修补施工速度,提高了修补质量[2]。环氧树脂-木材分层复合材料与木塑复合材料的出现,更是扩大了环氧树脂胶粘剂的研究前景与工程实践意义。
随着结构胶粘剂的使用,其流变性能日渐受到关注。近年来,国外研究胶粘剂主要往高强度方向发展,对胶粘剂的流变特性研究不够深入,且对于胶粘剂的动态黏弹性力学行为缺少必要的理论指导。流变学是研究物质流动和形变的科学,主要研究各种材料的蠕变和应力松弛的现象、屈服值以及材料的流变模型和本构方程。通过对高聚物流变性的研究,既可以为高聚物加工与应用提供理论依据,又可以从中获得分子结构与分子运动方面的信息,具有广阔的理论与应用前景。流变模型和本构方程可以为胶粘剂的老化机理提供理论依据,近年来出现的分数阶流变模型更是能预测其长期非线性黏弹性行为[3],为预测修补胶寿命奠定有力的理论基础。
1 动态黏弹性能测试
1.1 实验过程
实验采用的试样为自制环氧树脂胶粘剂,每100 g E51树脂加入14 g间苯二甲胺、4 g二乙烯三胺以及6 g活性稀释剂660A。其中,固化剂间苯二甲胺可提高树脂的耐热性能,二乙烯三胺可以有效降低树脂粘度,活性稀释剂可以进一步降低粘度,可增加渗透性,提高修补和加固效果。
试样制备过程:将原料混合,搅拌均匀后放入真空干燥箱(图1)中抽除气泡20 min,随后倒入模具,压制成15 mm×4.5 mm×2.5 mm试样。固化24 h后从模具取出,抛光打磨后放入70 ℃烘箱干燥8 h以消除残余应力,冷却后使用DMA-8000型流变仪(图2)进行DMA测试。测试采用应变控制的单点弯曲模式,应变为0.1%。在6个恒定温度水平下(30、40、50、60、70、80 ℃)各取3根式样测试其动态黏弹性频率谱,并求其平均值为实验数据。实验中荷载频率以指数递增的方式从0.01 Hz上升至100 Hz,以获得不同温度及频率下试样的储能模量E′、耗能模量E″及损耗角δ的变化情况。

图1 真空干燥箱Fig.1 Vacuum drying oven

图2 DMA 8000型流变仪Fig.2 DMA 8000 rheometer
1.2 实验结果
不同温度水平下频率与储能模量的关系由图3所示,储能模量E′表征的是材料的弹性形变。从图3可以看出,随着温度的升高,相同频率下的储能模量有下降的趋势;而随着频率的上升,储能模量增加,这与文献[4]的结论一致。材料的力学松弛行为通常受到频率与温度的共同影响。频率的增加或温度的降低,都会导致高聚物分子链段运动滞后于外力变化的程度增大,在宏观上表现为储能模量E′升高。
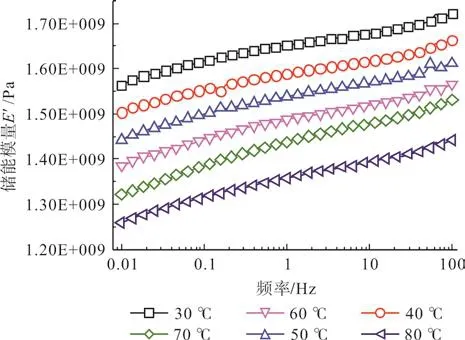
图3 不同温度水平下频率与储能模量曲线Fig.3 Curves of frequency vs storage modulus at different temperature levels
图4所示为不同温度水平下的荷载频率与耗能模量的关系,并使用origin软件对其进行拟合,使其趋势更加明显。耗能模量E″表征的是在形变过程中因黏性变形所损耗的能量。从图4可以看出,尽管在高频和低频时,耗能模量有一定的波动,但其仍然保持随着频率升高耗能模量下降的趋势。且随着温度的升高,材料的分子热振动加剧,内耗增大,在宏观上表现为耗能模量随着温度水平的升高而增大。

图4 不同温度水平下频率与耗能模量曲线Fig.4 Curves of frequency vs loss modulus at different temperature levels
2 数据分析
2.1 储能模量主曲线的构建
同一个实验对象的响应,既可以在低温条件下通过长时间的实验观察到,也可以在高温条件下通过短时间的实验观察到,称之为时间-温度等效理论[5]。通过该理论,可以实现两种实验条件下响应相互之间的量化转换,从而在有限的实验条件下拓展得到的实验数据,有利于对实验对象力学性能的研究。
根据时间-温度等效理论,以50 ℃为参考温度,在参考温度下测得的储能模量试验曲线不发生移动,将30 ℃及40 ℃下的曲线向左水平移动,60、70及80℃下的曲线向右水平移动,使所有曲线与50 ℃下的曲线形成一条曲线,就可以得到在12个数量级(10-6~106Hz)的频率下,储能模量与频率之间的关系,如图5所示。可以看出平移后得到的曲线整体较为光滑平整,说明时间-温度等效原理在小应变条件下可以描述该胶粘剂的动态黏弹性力学行为。
使用同样的方法,我们也可以得到在50 ℃的参考温度下,耗能模量的主曲线,如图6所示。
2.2 分数阶微积分理论
分数阶微积分有多种定义,流变学中通常使用黎曼-刘维尔分数阶导数[6]。设函数f(x),则其在a点处的α阶黎曼-刘维尔分数阶导数定义为:

图5 平移后的储能模量E′主曲线(T=50 ℃)Fig.5 Main curve of storage modulus E′ after translation(T=50 ℃)

图6 平移后的耗能模量E″主曲线(T=50 ℃)Fig.6 Main curve of loss modulus E″ after translation(T=50 ℃)

式(1)中:f(x)为任意函数,a表示函数求导处,α为求导阶数,m为大于α的最小的整数,另定义
2.3 基于分数阶微积分的Zener流变模型
整数阶流变模型由胡克弹簧与牛顿黏壶组成,其中胡克弹簧用来模拟材料的弹性行为,牛顿黏壶模拟材料的黏性行为,两者结合来表达材料的黏弹性性质。如图7所示的整数阶Zener模型,可以通过各元件之间的力学关系推导得知其本构方程为:

式(2)中:E1、E2分别为整数阶Zener模型中两个弹簧的模量,η为黏壶的模量,σ为材料所受的应力,γ为材料的应变。设应力σ=Eγ0sin(ft)并将其带入(2)式,经过傅里叶变换,分割总模量中的实部与虚部推导,可得:

式(3)与式(4)中,τ=η/E2,其具有时间的量纲,称为延迟时间。
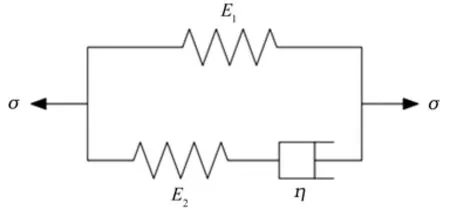
图7 整数阶Zener模型Fig.7 Integer-order Zener model
分数阶流变模型即将传统的牛顿黏壶替换为分数阶阻尼器[7]。其本构方程为:

式(5)中,α为分数阶阻尼器的阶数,且满足0<α<1,t为时间,G为物体的模量,ε为应变。
与传统流变模型中的元件比较,可见当α趋近于0时,元件性质更贴近于胡克弹簧;当α趋近于1时,元件性质更贴近于牛顿粘壶。因此,分数阶阻尼器处于理想胡克弹簧与理想牛顿粘壶之间,更能体现出物体的非线性黏弹性属性。
分数阶Zener流变模型如图8所示,其对应的本构方程的推导过程与整数阶Zener模型一致,可得出其动态黏弹性本构方程为:
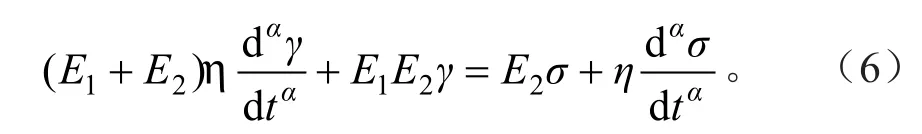
设应力σ=Eγ0sin(ωt)并将其带入(6)式,经过傅里叶变换,分割总模量中的实部与虚部推导,可得:

式(7)与式(8)中,τ=η/E2,其具有时间的量纲,称为延迟时间。
2.4 拟合结果
通过使用不同分数阶数的流变模型对实验所得数据进行拟合,可以得到表1中的拟合参数。可以看出随着分数阶数α值的下降,拟合结果中决定系数R2更趋向于1,因而说明模型的拟合更加精确。

图8 分数阶Zener模型Fig.8 Fractional order Zener model

表1 不同阶数流变模型拟合结果Table1 Fitting results of rheological models with different orders
图9为储能模量拟合结果与实验数据的比较。其中实验数据为通过时间-温度等效原理平移后得到的宽频率下频率-模量主曲线,其他各条曲线为不同阶数的流变模型带入参数后模拟的曲线。可以看出随着分数阶数的下降,拟合曲线不断向实验数据接近。

图9 f与E′的试验曲线与流变模型拟合曲线Fig.9 Experimental curves and rheological model fitting curves of frequency f vs storage modulus E′
图10为耗能模量的拟合结果与实验数据的比较,实验数据为平移后宽频率下的频率-模量主曲线。随着分数阶数的下降,拟合结果也在向实验数据接近。与此同时,对耗能模量的拟合效果没有储能模量好,原因包括测试温度的个数选择不够多,固体储能模量的测量容易出现误差等。

图10 f与E″的试验曲线与流变模型拟合曲线Fig.10 Experimental curves and rheological model fitting curves of frequency f vs storage modulus E″
3 结论与讨论
分数阶流变模型是近年来流变学讨论的热点,其主要改进是使用分数阶阻尼器代替传统的牛顿黏壶。其中分数阶阻尼器的物理意义可以理解为:描述介于胡克弹簧与牛顿流体之间的中间材料的本构关系元件。从理论上说,该种模型应该更贴近非线性黏弹性材料的真实力学特性。
本研究通过对动态黏弹性实验结果进行分析,得到以下结论:
1)通过时间-温度等效原理,将不同温度下的频率-模量曲线进行平移,建立了50 ℃下自制环氧树脂胶粘剂的频率-模量主曲线,使得实验数据从10-2~102Hz数量级拓展为10-6~106Hz,从而可以用较窄频率范围内的实验数据推导得到宽频率下的实验数据;
2)在较宽频率的范围内,分数阶流变模型的拟合效果比传统的整数阶流变模型好。相比于整数阶的决定系数R2为0.818,分数阶的决定系数R2最低也为0.852;且随着分数阶数的降低,拟合效果不断升高,在α=0.2时达到最高的0.984 9。说明分数阶流变模型其对非线性黏弹性行为的拟合有着不可替代的优势。
但由于高分子材料黏弹性能及实际工程应用中的复杂性,加之课题组时间精力有限,有关高分子材料的动态黏弹性力学行为的研究仍有进一步发展和完善的空间。例如,进一步优化与改良分数阶流变模型,并研究不同阶数的分数阶模型对材料模拟结果差异的原因;深入探讨胶粘剂与木材形成的复合材料的流变性能等均将是今后的研究重点和主攻方向。

