基于AIC准则判断锂电池最优模型
李国春,王恩龙,王丽梅,盘朝奉
(1.江苏大学 汽车与交通工程学院,江苏,镇江 212013;2.江苏大学 汽车工程研究院,江苏,镇江 212013)
当前电动汽车相关技术飞速发展,电池管理系统(Battery Management system,BMs)作为新能源汽车技术的重要组成部分,受到国内外科研人员的广泛关注。目前,主要有等效电路模型[1]、电化学模型[2]及神经网络模型[3]用于BMs开发中。这3种模型在模型参数辨识方法、使用范围及模型精度等方面各有优势,但大多数研究只关注电池模型的预测精度,而忽视模型结构复杂度和预测精度之间的平衡问题[4]。对于基于嵌入式系统所开发的BMs而言,电池模型的精度与复杂度将影响电池管理系统的决策和控制,因此,精确建模和模型简约之间的权衡是BMs开发中一个难以避免的关键问题[5-6]。
本文选用不同阶次的等效电路模型对动力电池进行建模研究,基于赤池信息量准则对模型的结构复杂度和预测精度进行系统的评价和分析,得到最适合工程应用的动力电池模型。
1 电池模型建立及数学描述
1.1 电池模型建立
n阶RC等效电路模型的原理图如图1所示。该模型由电压源、欧姆内阻、不同阶次RC网路(i=0,…,n)组成,其中,Uoc为电池开路电压,R0为电池欧姆内阻,Ri为电池极化内阻,Ci为电池极化电容,Ri和Ci并联用于模拟电池动态特征,U为电池端电压。
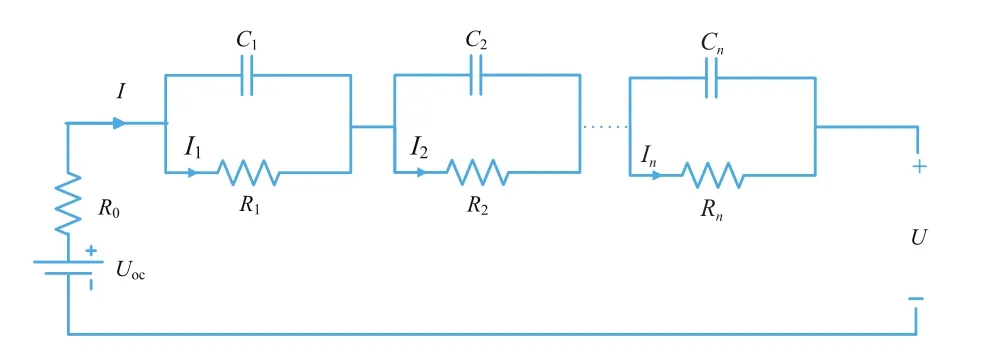
图1 n-RC等效电路模型原理
1.2 模型数学描述
基于基尔霍夫定律,建立上述n-RC等效电路模型电路描述方程,具体表达式为:
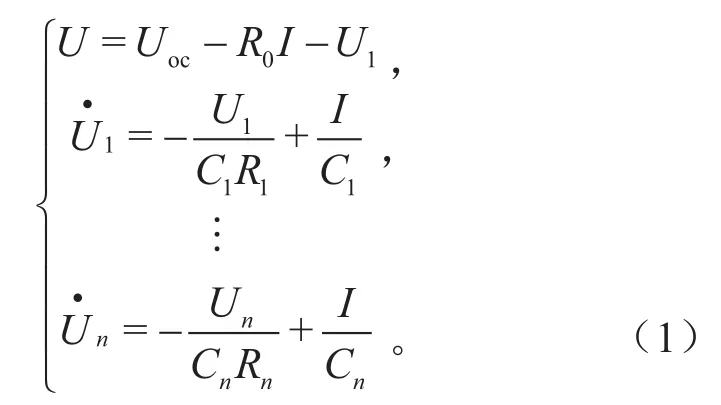
式中:i=0,…,n;Ui为极化电压,V。对Ui进行离散化求解可得:
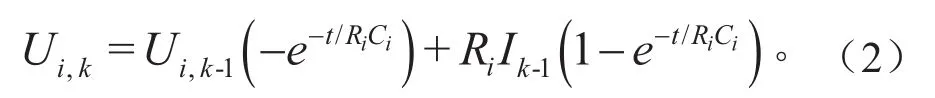
式中:t为系统采样周期;Ik为k时刻的电流;Ui,k为第i个RC网路在k时刻下的极化电压;如果已知模型参数和电流电压值,可得:
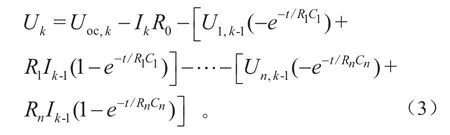
1.2.1i= 0
当i=0时,n-RC等效电路模型可转化为Rint模型,根据式(3),电池输出电压与输入电流关系如下:
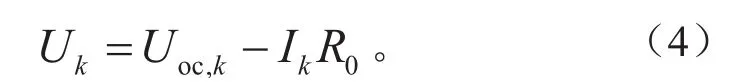
采用Z变换法将模型推导为基于时域的数学表达式,将式(4)转化为输入输出方程yk=θkΦk形式可描述为:
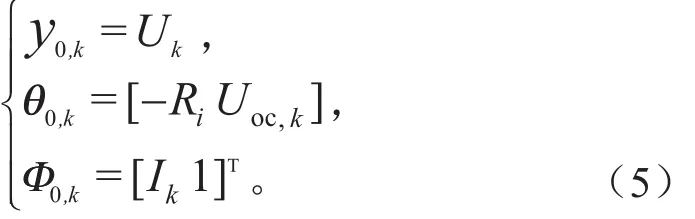
为区分方便,采用下标的方式描述模型阶次n,如y0,k表示模型阶次为0时系统的输出变量,■表示模型阶次为0时系统的系数矩阵,表示模型阶次为0时系统数据矩阵,下角标k表示数据值为tk时刻的值。
1.2.2i= 1
当i=1时,n-RC等效电路模型转化为Thevenin模型,假设:根据式(3),则电池输出电压与输入电流的数学关系如下:
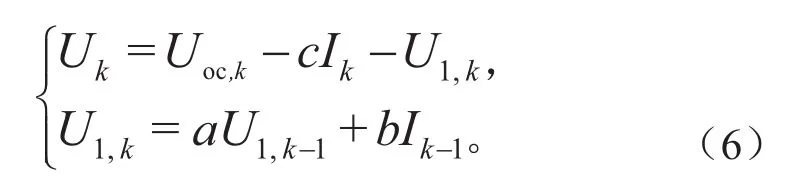
针对极化电压Ui,从离散时间转换到Z域如下:
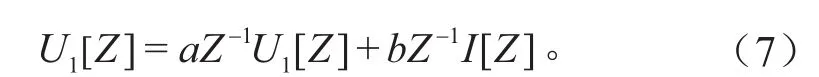
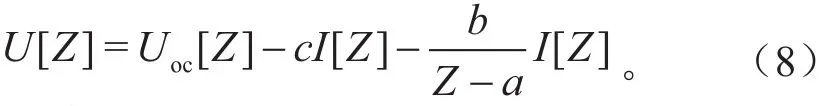
整理可得:
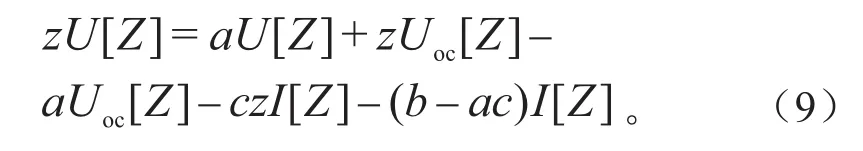
求逆拉普拉斯变换可得:
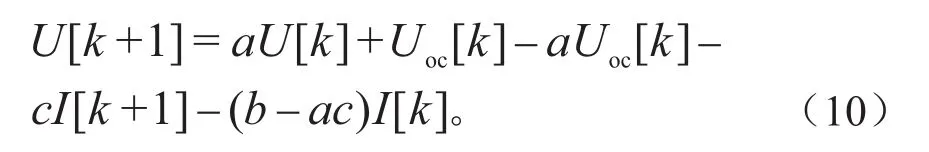
将式(10)转化为输入输出方程yk=θkΦk,得:
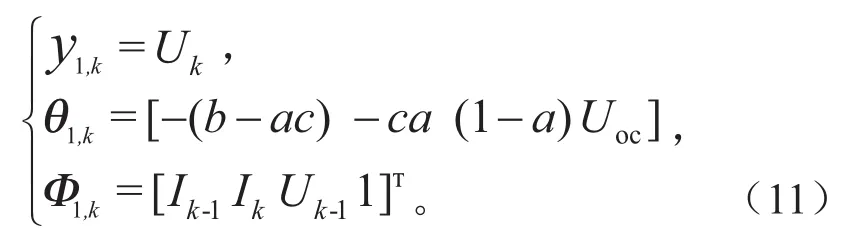
其中,欧姆内阻和开路电压可从式(11)中推导出,表达式如下:
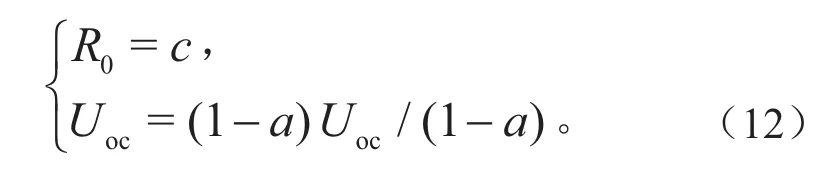
1.2.3i= 2
当i= 2时,n-RC等效电路模型转化为DP模型,假设:根据式(3),则电池输出电压与输入电流的数学关系如下:
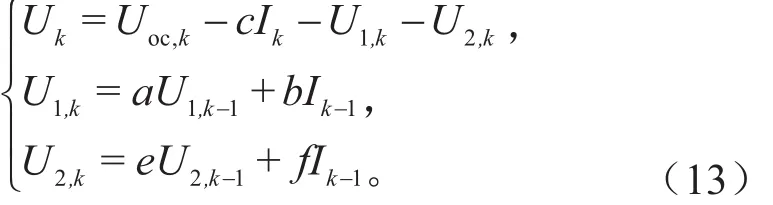
将其代入式(13)中得:
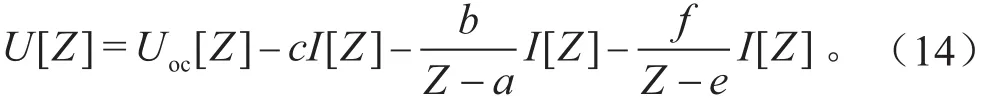
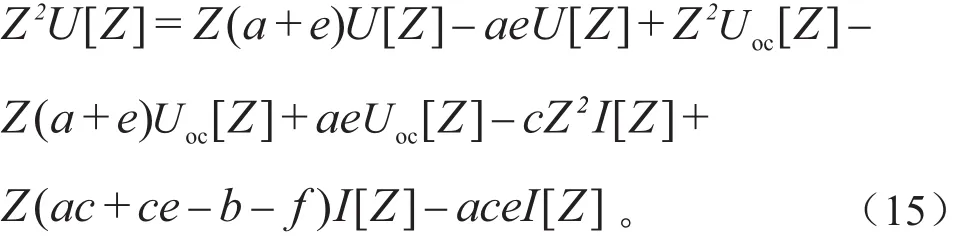
求逆拉普拉斯变换可得:
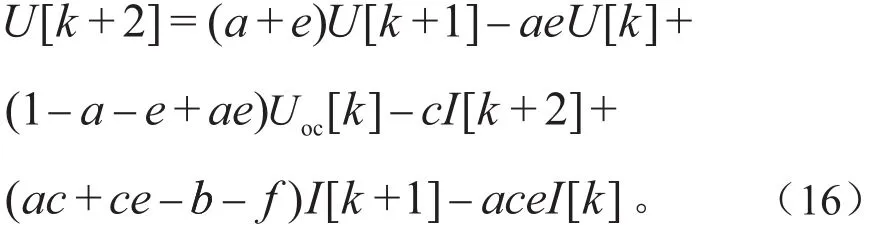
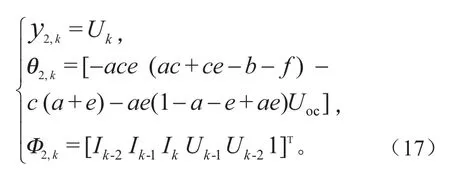
其中,欧姆内阻和开路电压可从式(17)中解析出:
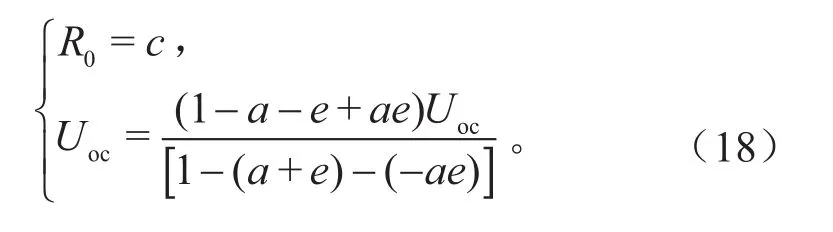
1.2.4i=n
当i=n时,电池输出电压与输入电流的数学关系如式(3)所示,根据Z变换法则,可将式(3)化简为:
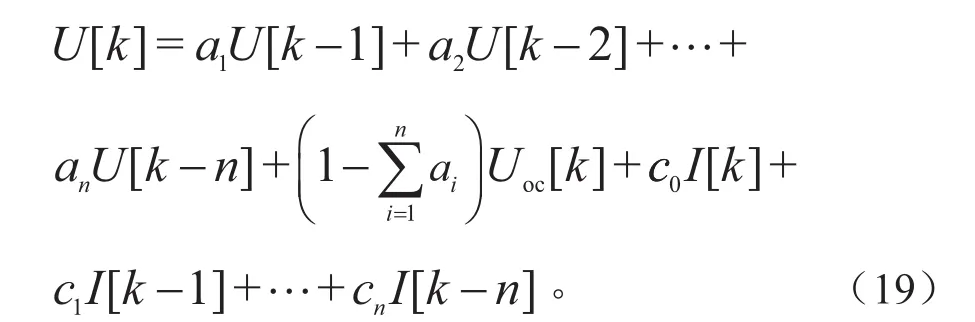
式中:ai(i=1,…,n),ci(i=0,…,n)为模 型 的辨识参数。同理,可将该式转化为输入输出方程yk=θkΦk的形式,如下:
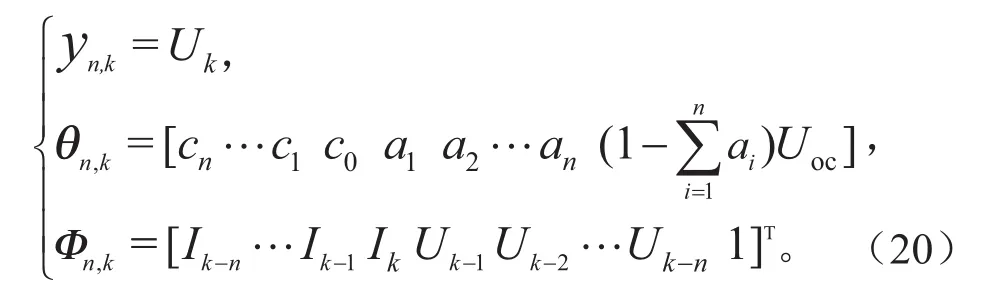
其中,欧姆内阻和开路电压可以基于式(12)和式(18)的规律推导得出:
2005年以来,黄河流域水质总体恶化趋势初步得到遏制。其中,黄河干流水质呈好转趋势,主要支流水质类别虽无较大变化,但主要污染物浓度有所下降,尤其以污染较重的渭河、洛河较为明显。
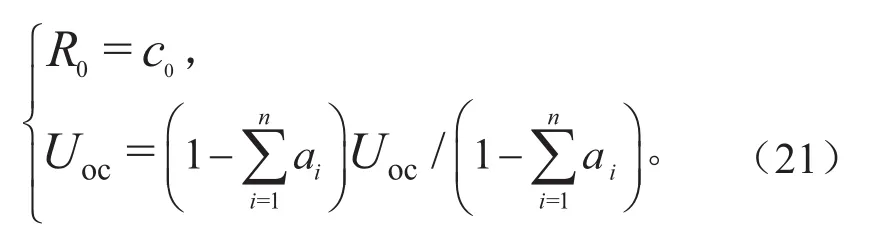
当模型的阶次较高时,系统的系数矩阵难以推导,当n>60后,单位采样时间内电池荷电状态(state of Charge,sOC)对时间的变化率不再近似等于0,而是逐渐接近2%[7]。同时,较高阶数的模型复杂度也会相应增加,不利于动力BMs的运算。因此,本文仅讨论模型阶数在3阶以内的情况。
2 模型参数辨识
2.1 模型参数离线辨识
本研究使用的电池单体为江苏春兰新能源公司生产的40 Ah/3.7 V的方形三元材料锂动力电池,电池外形尺寸为36 mm×130 mm×150 mm。混合脉冲功率特性(Hybrid Pulse Power Characterization,HPPC)、简化联邦城市行驶工况(Dynamic stress Cycle,DsT)试验充放电设备是宁波拜特有限公司提供的动力电池测试系统NBT30V100AC4-T系列。无锡索亚特小型高低温湿热交变试验箱提供相应的环境温度和湿度条件。所有试验在恒温 25 ℃,湿度30%的工况下进行。
等效电路模型中需辨识参数有开路电压Uoc、欧姆内阻R0、极化内阻Ri及电容Ci。建立这些参数与sOC间的函数关系,在实际应用过程中,通过估算得到的sOC即可获取相关模型参数,进而实现电池电压的预测。本文参考《FreedomCAR电池实验手册》里的混合脉冲试验原理,利用HPPC试验数据进行模型参数辨识,辨识原理如图2所示。
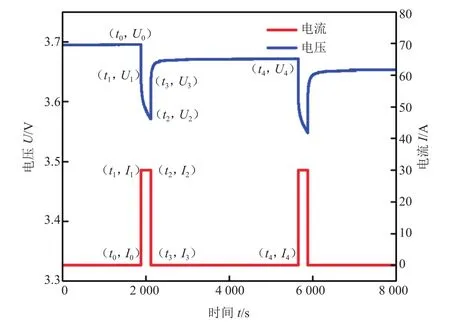
图2 脉冲放电过程中部分端电压和电流相应曲线
图2中,t1至t2时间段电池电压变化过程称为零状态响应,t3至t4时间段电池电压变化过程称为零输入响应。根据零状态响应建立放电阶段方程:
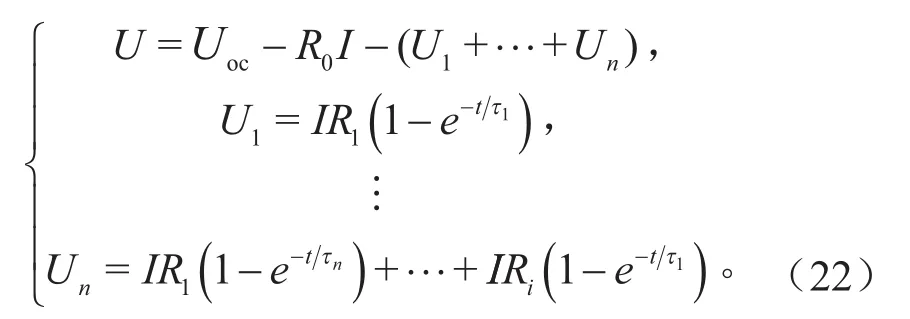
式中:τi为时间常数(τi=RiCi)。本文采用文献[8]中的指数拟合法得到模型中的RC网络的参数,指数拟合函数的表达式为:
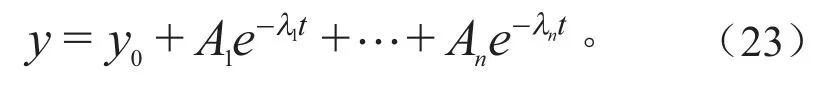
比较式(22)和式(23)可得:
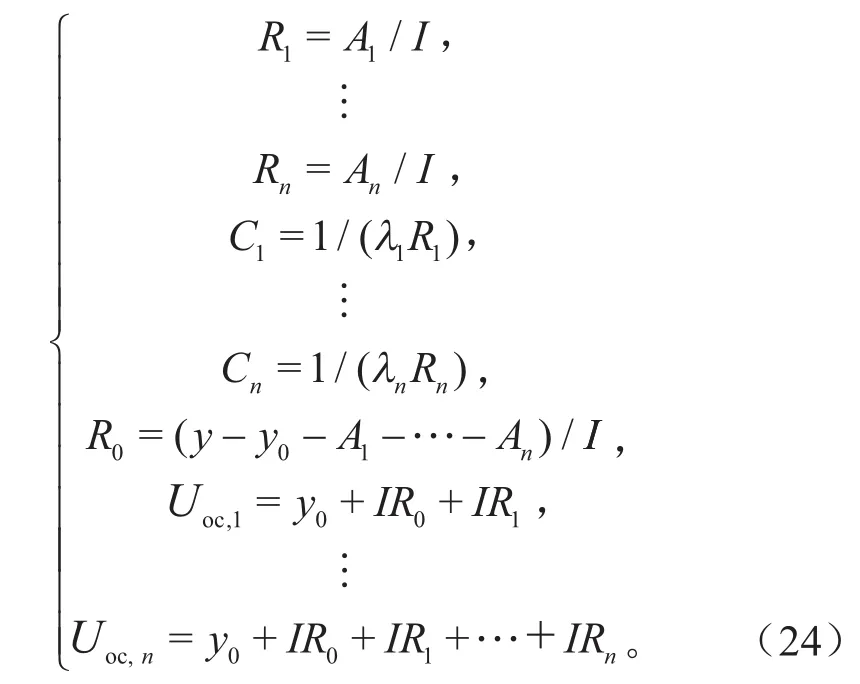
通过式(24)可以计算出模型中的各个参数。但使用该方法求取R0的过程中,因开路电压(Open Circuit Voltage,OCV)与sOC的函数关系耦合影响会给平台电压区带来较大误差,所以将采用下面的方法求解电池欧姆内阻。
由图2可知,在放电开始时刻电池电压出现阶跃式下降。这是电池欧姆内阻造成的,所以可通过式(25)计算电池欧姆内阻:
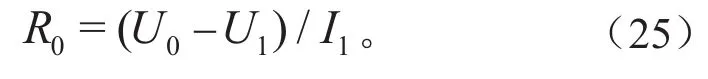
2.2 模型参数在线辨识
由于电池系统的时变性,实际应用中的模型参数会随着循环次数、电池容量、外界温度等因素发生改变,采用初始辨识参数估算出长期使用后的电池特性会产生较大偏差。因此,需实时测量电池电流、电压和温度来对模型参数进行在线辨识,以保证模型精度与适应性。
参数在线辨识的方法主要有遗传算法、最小二乘法、极大似然算法、卡尔曼滤波法和预报误差法等。随着计算步数的无限增加,原始数据的积累会越来越多,致使新输入的数据很难对前面的估计值做出修正,从而影响对其后的参数估计效果,且在实时系统中可能表现得更为明显。为了避免类似情况,提出了含有遗忘因子λ的递推最小二乘法 ——遗忘因子算法 (Forgetting Factor Algorithm,FF),它能够有效克服“数据饱和 ”,防止估计发散[9]。FF的基本计算方程为:

式中:ek为零均值白噪声,符号定义与式(20)一样,含有遗忘因子λ的递推最小二乘法的公式为:
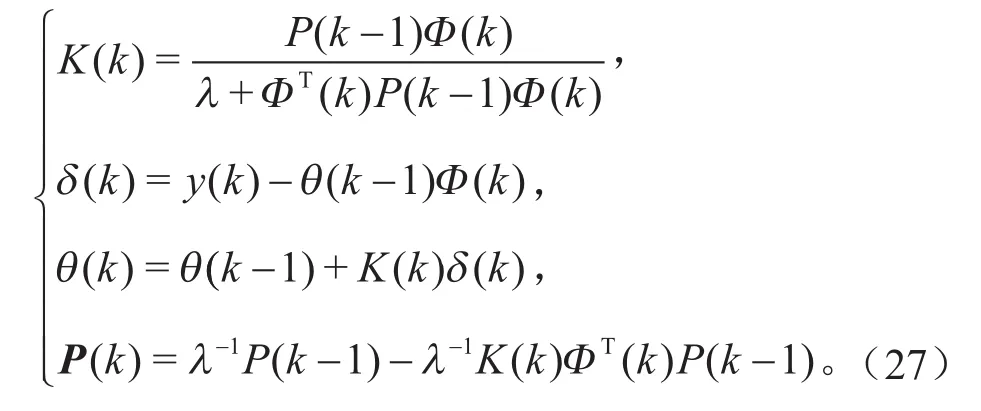
式中:λ为遗忘因子,一般情况下λ=0.95~1,λ越小,算法跟踪能力越强,但也有可能会引起算法的波动,当λ=1时,式(27)即为普通的递推最小二乘法;K为算法增益;P为状态估计值的误差协方差矩阵。
3 模型阶次选择
3.1 基于离线参数的建模方法
根据2.1节采用的动力电池参数离线辨识方法,可得到各个阶次模型的不同sOC下的模型参数。根据这些参数基于simulink平台建立不同RC网络结构的等效电路仿真模型,以Thevenin 模型为例,如图3所示。其中,模型参数采用simulink元件库中的1-D Lookup Table建立Map来映射关系,如图4所示。
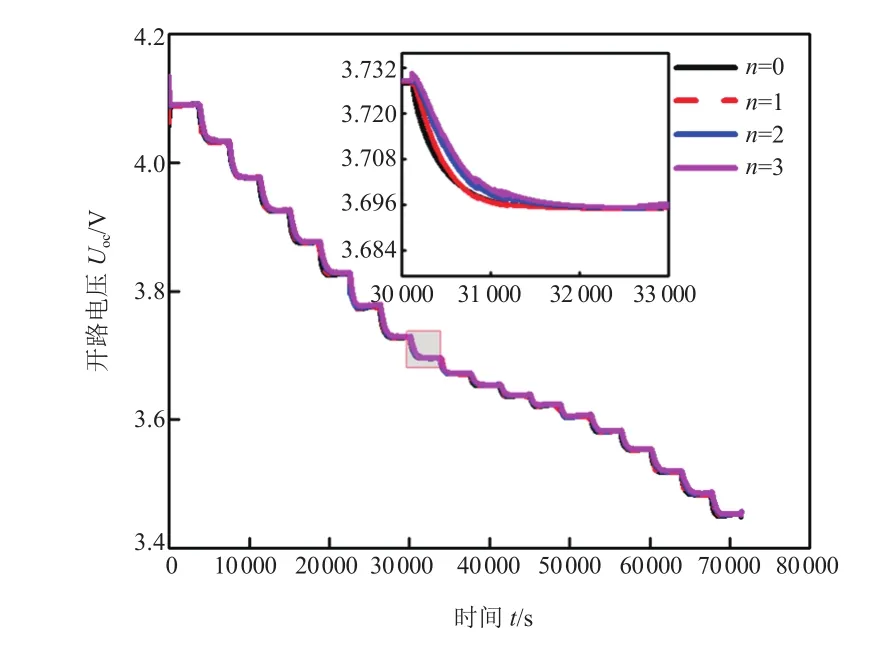
图5为不同阶次电池开路电压的辨识结果,图6为电池不同阶次模型的预测误差对比。由图5可知,带有RC网络结构的等效电路模型开路电压的辨识
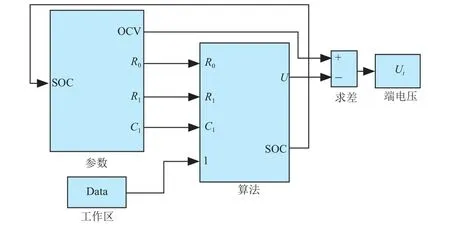
图3 动力电池simulink仿真模型
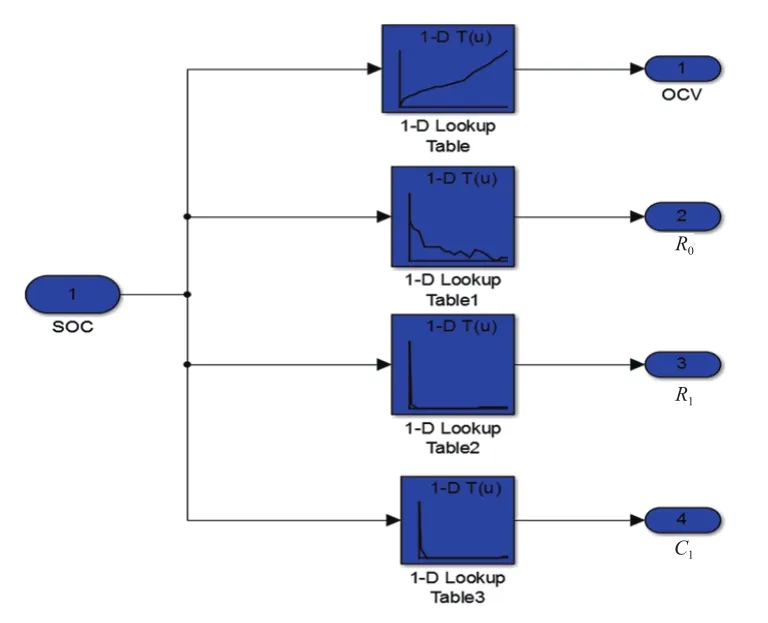
图4 利用1D Lookup Table建立的模型参数Map图
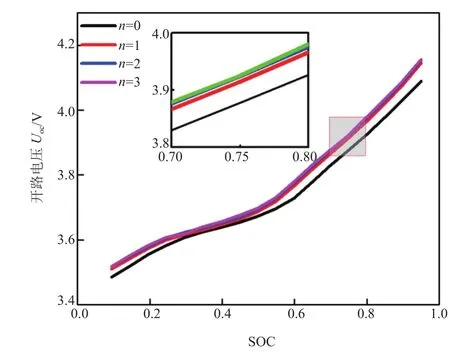
图5 基于HPPC工况的单体开路电压辨识结果(离线)
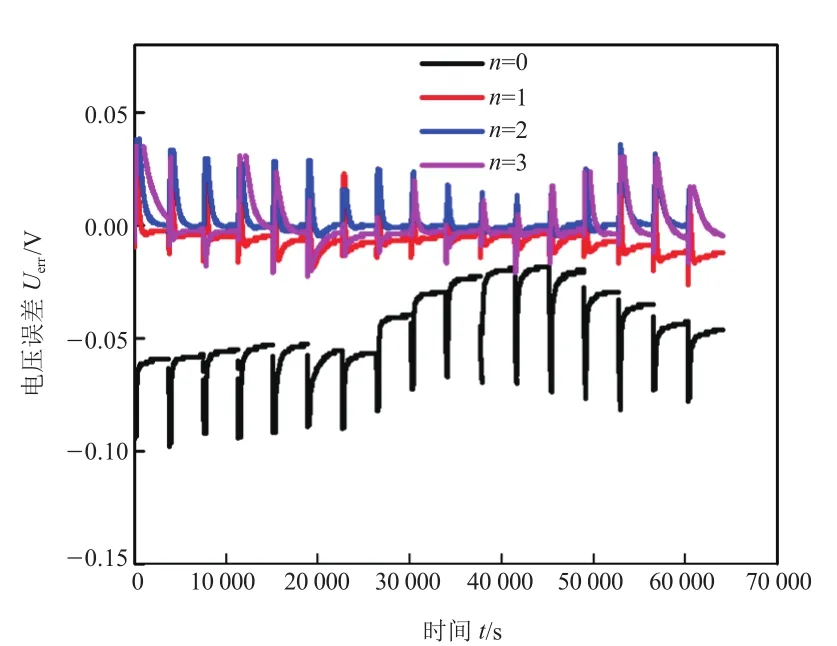
图6 基于HPPC工况的单体电压辨识误差(离线)
结果较为接近,平均偏差只有2.3 mV,而基于Rint模型的开路电压辨识结果与带有RC网络结构的模型偏差较大,最大偏差达53.4 mV,平均偏差也在30.7 mV。为比较各阶数模型的精度与效率,采用相关程度评价系数R-square,以及误差绝对值的最大值、平均值、标准差、仿真计算时间这5个参数来进行不同RC网络等效电路模型精度的分析与评价,见表1。其中,R-square值是由各个模型参数辨识过程中,相同sOC区间的数据拟合得到的,其值可以反映拟合程度的好坏,越接近1,说明拟合结果越好。为了客观评价误差值,所有误差统计结果均使用预测误差的绝对值。例如,表1为使用上述5个参数来进行不同RC网络等效电路模型精度分析与评价的结果。
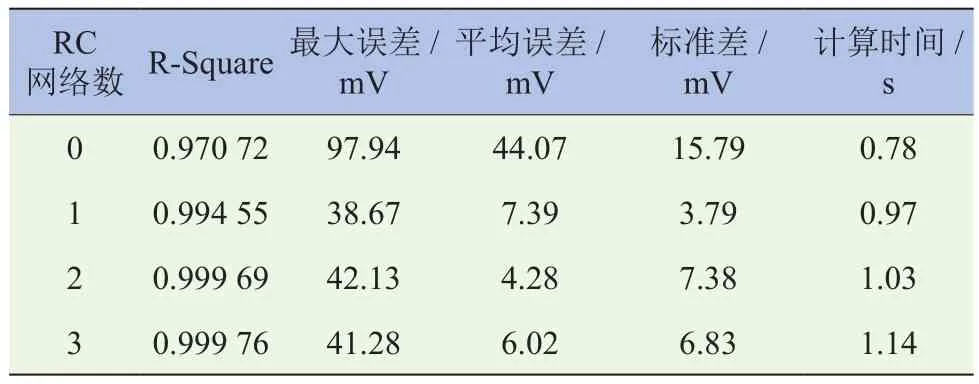
表1 基于离线参数的电压预测误差
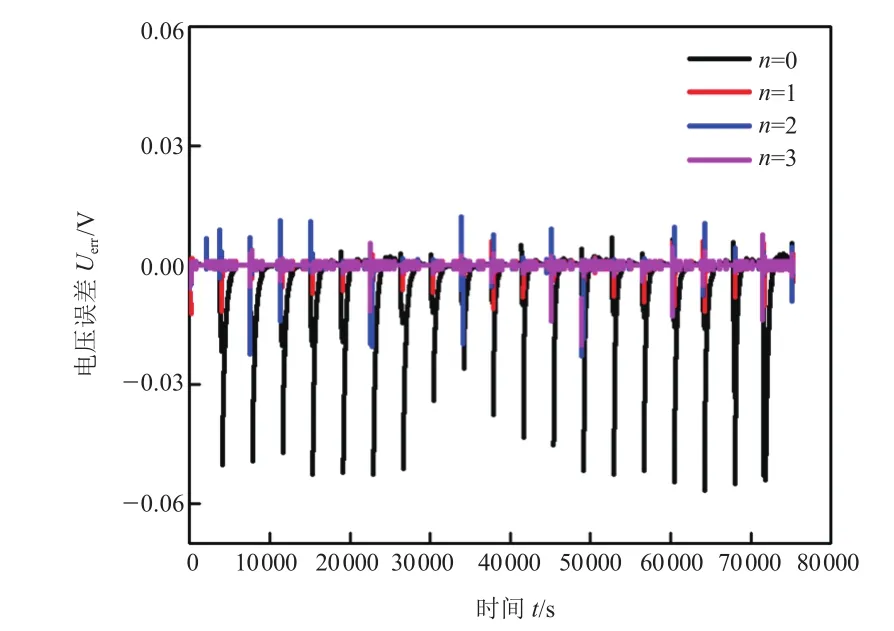
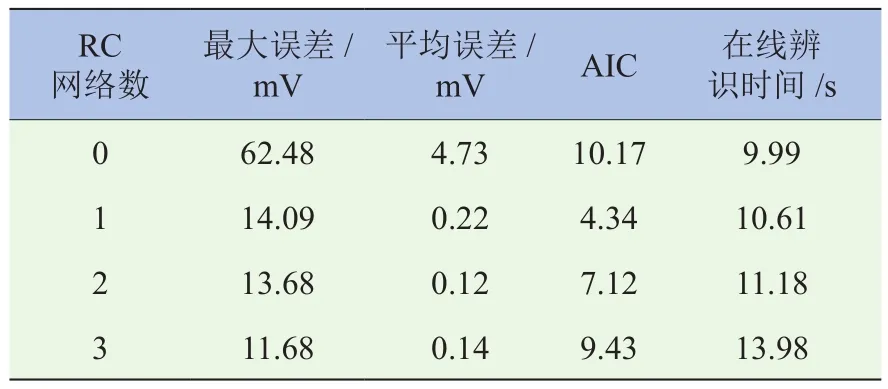
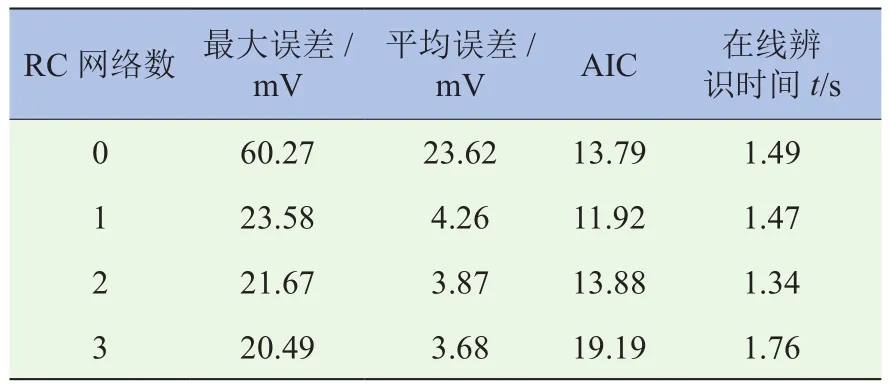
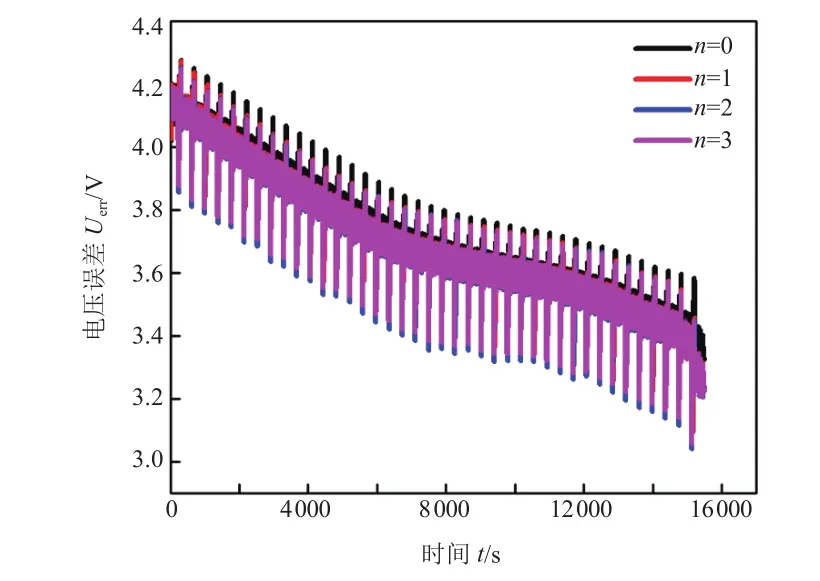
由表1可知,Rint模型的R-square值最小,电压预测误差较大,最大误差为97.94 mV,而带有RC网络结构的模型,其预测电压误差在45 mV以内,可见,若不考虑RC网络结构,电池开路电压辨识结果与模型预测电压误差较大,因此,Rint模型并不适用于电池特性描述。为权衡模型精度与复杂度,根据式(28)和式(29)计算前三阶等效电路模型的赤池信息值[9]。由于n< 式中:L为数据的长度;为最优参数下的平方和,计算公式为: 式中:yk为电池端电压的测量值;为基于模型的端电压仿真值。计算结果见表2。 若以AIC作为判断模型精度和复杂度的指标,AIC越小,模型越优,当n=1时,AIC最小,即Thevenin 模型更适合描述三元锂离子动力电池。由于Rint模型精度低,其AIC的值大于Thevenin模型和DP模型;根据表1结果可知,带有RC网络结构的模型预测精度并不悬殊,结合表2可以看出,模型复杂度是影响AIC值的主要因素,因此,Thevenin模型最优。 表2 基于离线参数的AIC 根据多次辨识经验,选定遗忘因子为 0.999进行在线参数辨识,辨识结果如图7和图8所示。 图7 单体开路电压辨识结果(在线) 图8 单体电压辨识误差(在线) 图7为在线辨识的前三阶RC等效电路模型开路电压,图8为前三阶RC等效电路模型估计电压误差对比。由图7可知,不同RC网络结构电池模型辨识的开路电压值较为接近,四者之间的最大偏差为19.35 mV,平均偏差为2.75 mV,表明使用在线辨识法得到的开路电压随sOC的变化关系较用离线辨识法得到相应关系更为精确。由图8可知,带有RC网络结构的等效电路模型电压预测误差相差不大,都在15 mV以内,而不带RC网络结构的等效电路模型电压预测误差最大达到62.48 mV,同样验证了Rint模型并不适合三元锂离子电池。为详细分析和评价模型的估计精度,使用不同RC网络模型估计误差的绝对值进行统计分析,结果见表3。 表3 基于HPPC工况的电压预测误差 由表3可知,Rint模型不论是平均误差还是最大误差都远高于其它阶次模型,其AIC值最大。通过对不同阶次模型误差的绝对值进行统计分析,尽管n=3时的预测最大误差优于n=2,但RC网络数越多,辨识时间越长,增加了计算时间。通过AIC可得出,n=1时的模型最优。为验证该方法的适应性,同时使用DsT工况进行分析,单体电压辨识结果如图9所示,计算结果见表4。 表4 基于DsT工况的电压预测误差(在线) 由于DsT工况电流变化较为复杂,根据统计数据分析可知,不同阶次等效电路模型的最大误差、平均误差及AIC值与HPPC工况相比较数值增大,但是根据AIC判定,同样可以得到n=1时的模型最优。 综上所述,基于离线和在线参数的建模方法均得到Thevenin 模型最适合三元锂离子动力电池建模。通过比较图6、图8和表2、表3,基于在线数据的参数辨识方法得到的开路电压和端电压比使用离线数据参数辨识方法得到的相应结果更优。 图9 单体电压辨识结果(在线) 本文基于AIC,充分考虑了模型离线和在线参数辨识方法的优缺点,提出了定量评价模型结构复杂度和预测精度综合性能函数,以判断锂离子电池最优模型。通过离线和在线参数的建模方法,对不同RC阶次的等效电路模型进行AIC分析,结果表明,一阶RC等效电路模型最适合锂离子动力电池精确建模。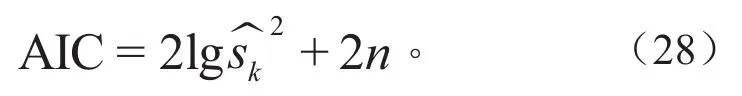
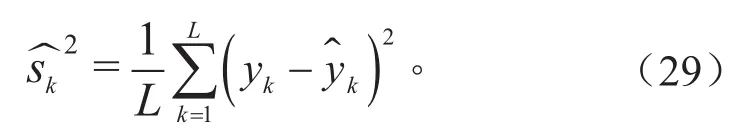

3.2 基于在线辨识参数的建模方法
4 结论

