带有缺失数据的Box-Behnken试验设计

张刘方 丁宇 陈雪平 马强

摘    要：中心组合设计是响应曲面设计的重要内容，需要通过试验、建模、数据分析，从而选择最优设计方法。研究重点介绍了Box-Behnken设计（BBD设计），然后探讨了试验在缺失一个数据后，若干效率准则的变化（包括D-效率，E-效率，A-效率），讨论了各类设计中不同部分缺失一个数据时的效率值变化。结果表明，效率随因子数的变化呈现相同的趋势;最后，给出了使得效率损失最小的设计方案。

关键词：Box-Behnken设计;D-效率;E-效率;A-效率

中图分类号：O224             文献标识码：A              文章编号：2095-7394（2019）06-0082-06

响应曲面设计是试验设计的一种。试验设计是使用频率最高的统计方法之一，最早由英国统计学家费歇尔（R. A. Fisher）在1935年提出，至今已有80多年的历史。在试验设计的发展道路上，大致经历了四个阶段，即传统的方差分析、正交试验设计、信噪比试验设计与产品的三次设计、电脑仿真试验。其基本思想是对试验方案做出合理安排，使试验数据有合适的数学模型，以减少随机误差的影响，从而提高试验结论的精度和可靠度[1]。

Box-Behnken设计由Box和Behnken在1960年提出，是由因子设计与不完全集区设计结合而成的适应响应曲面设计的三水平设计。Box-Behnken设计非常重要的特性是以较少的试验次数，去估计一阶、二阶与交互作用项[2]，并且在因素数相同的情况下，Box-Behnken设计的试验次数要比中心组合设计的次数少，所以更经济，可称为具有更高效率的响应曲面设计法。 它是一种符合旋转性或几乎可旋转性的球面设计[3]。

1    效率值计算

1.1  D-效率

试验设计评定效率准则中最常用的是D-效率[4]，它是用矩阵的形式来判定试验设计是否最优的一种准则，用到的矩阵是[XTX]。但是，在带有一个缺失数据时，采用的矩阵是[XTrXr]。同[XTX]一样，[XTrXr]也包含方差和协方差，控制设计方案的主要方法就是控制这个矩阵的方差和协方差。 讨论矩阵的一个重要标准是行列式，把矩阵[（XTrXr）-1]的特征值[λ1，λ2…，λp]的最大特征值、算术平均特征值和几何平均特征值用[λmax]、[λ]和[λ]来表示，则[D0=XTrXr=i=1pλ-1i=λ-p]。为了消除试验次数和因子个数带来的影响，可以定义[D=（n-1）-1XTrXr1/p]，其中[p=（k+1）（k+2）/2]。[p]是在具體模型中的参数个数，[n]是总的试验次数。 D-效率设计就是求[XTrXr]的最大化，也就是说求[MaxζXTrXr（ζ）]，其中[ζ]表示不同的设计序号[5]。

1.2  A-效率

1.3  E-效率

2    Box-Behnken设计

2.1  对BBD设计进行方案设计

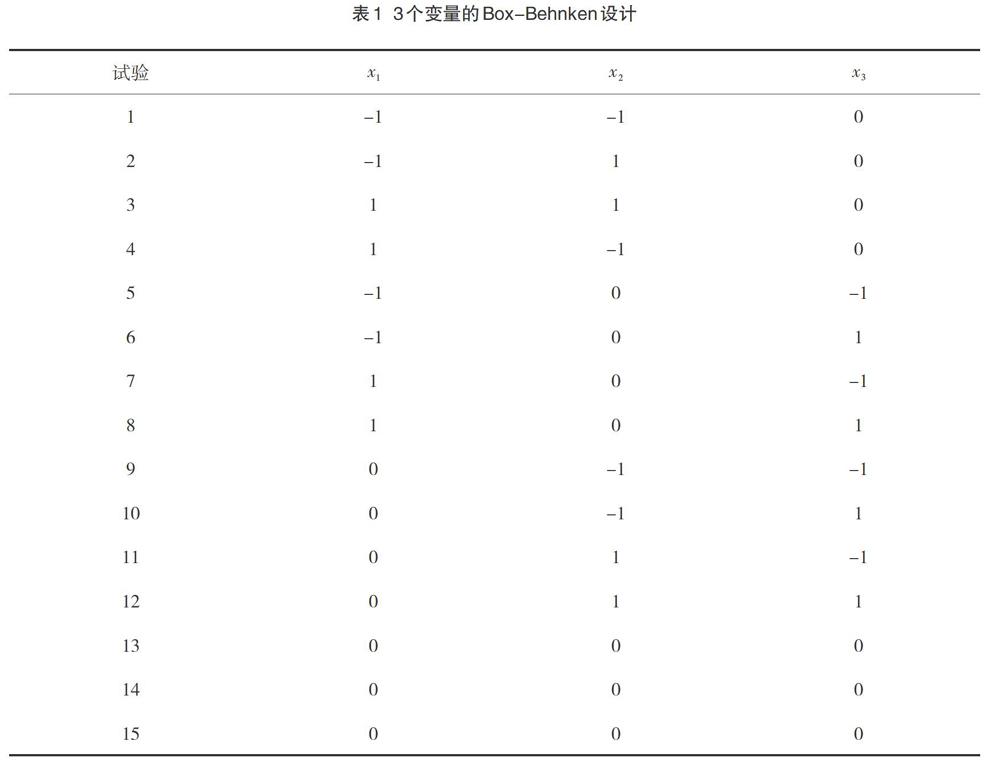
在因子为3时，设计方案（K=4、5、6时的设计方案与K=3时相似，所以表1只列了K=3时的设计方案）见表1。

2.2  将设计的方案进行试验，得到数据并进行BBD设计的效率值分析

从表2中可以直观看出，各效率值的变化与没有缺失数据的效率值基本保持一致。即随着因子数的增加，各效率值在不断降低。其中D-效率降低幅度值较大，A-效率和E-效率降低幅度值较小。

由表3可以明显地看出，效率值变化趋势和表2情况一致。综合可以得出以下结论：不管这一缺失数据发生在Box-Behnken设计的哪一行，在强度相近或相同的情况下，随着因子数的增加，D-效率、A-效率、E-效率都呈递减趋势。

3    APM设计、CCD设计、BBD设计的比较

由于Augmented Pairs Minimax Design（APM设计）、Central Composite Design（CCP设计）、Box-Behnken Design（BBD设计）的每种设计各部分缺失一个数据的效率值发生趋势是基本相同的，所以仅用第一部分带有一个缺失数据的APM设计的效率图与原点处带有一个缺失数据的Box-Behnken设计的效率图进行对比。如图1，不难发现APM设计和BBD设计的A-效率、E-效率，均随着因子数的增加而减少，而APM设计的A-效率、E-效率趋向于零，D-效率与上两种设计有很大的差异。

比较图2、图3可以看出：CCD设计的A-效率、E-效率与BBD设计基本一致，都呈递减趋势，只是BBD设计的A-效率值、E-效率值在K=3时略大于CCD的A-效率值、E-效率值;而两种设计的D效率值相差较大，BBD设计的D-效率值随着因子数的增加不断降低，而CCD的D-效率大体上递减，但在因子数为5、试验次数为30（对应横坐标第一个5）时D-效率较低，在因子数为5、试验次数为46（对应横坐标第一个5）时D-效率又升高至0.55，在因子数为7时D-效率值下降到0。

综上所述，不同的设计在缺失一个数据的情况下三种效率值有一定的相似之处。即：A-效率值和E-效率值都较小且呈递减趋势;D-效率值较大但几乎没有规律可循。在缺失一个数据的情况下，这一现象也是符合实际要求的，即A-效率值、E-效率值越小越好，D-效率值越大越好。

4    因子数一定时的最优设计

4.1  K=3时，三种设计的各效率值比较

K=3时，由表4可以看出，APM设计的D-效率值最高，A-效率值、E-效率值最低。此时，在缺失一个数据时APM设计最优。

4.2  K=4时，三种设计的各效率值比较

K=4时，由表5可见，CCD设计的D-效率值最高，其A-效率值略低于其它两种设计，而三种设计的E-效率值几乎相等。所以，此时CCD设计较优。

4.3  K=5时，三种设计的各效率值比较

K=5时，从表6中可以看出，CCD设计的D-效率最高。同时，其A-效率、E-效率最小。此时，CCD 设计最优。

4.4  K=6时，三种设计的各效率值比较

K=6时，从表7可见，D-效率最高的依旧是CCD设计，BBD设计的A-效率、E-效率最低。所以，若以D-效率为判别准则，则选用CCD设计;若以A-效率、E-效率为判别准则，则选用BBD设计。

5    结语

通过上文讨论可以发现：不同的设计其效率损失也不同;因子数不同时，所表现出的效率损失也不尽相同。我们可以根据因子数的不同，选择不同的设计，使得效率损失最小。通过对每种设计都采用三种效率准则计算，发现在不同效率准则下，最优设计也存在差异。同时，还可以发现对于每种设计，不管是哪一部分带有缺失数据，效率随因子数的变化呈现相同的趋势。最后，在因子数相同的条件下，将不同设计在不同效率准则下的效率值进行归类。结果表明：在因子数较小时，CCD设计优于BBD设計和APM设计。

参考文献：

[1] 赵选民.试验设计方法[M]. 北京：科学出版社，2006.

[2] 陈立周. 稳健设计[M]. 北京：机械工业出版社，2000.

[3] WHITTINGHILL D C. A note on the robustness of Box-Behnken designs to the unavailability of data[J]. Metrika， 1998， 48（1）：49-52.

[4] DRAPER N R. Small Composite Designs[J]. Technometrics，1985，27（2）： 173-180.

[5] LEE C P . D-Optimal Designs for Second-Order Response Surface Models on a Spherical Design Region with Qualitative Factors[D].Gaoxiong： NSYSU，2011.

[6] 方开泰，刘民千，周永道. 试验设计与建模[M]. 北京：高等教育出版社，2011.

[7] XU Hong-quan， JAYNES Jessica，DING Xian-tiang. Combining Two-Level and Three-Level Orthogonal Arrays for Factor Screening and Response Surface Exploration[J].Statistica Sinica，2014，24（1）： 269-289.