基于绿灯时间的交通子区划分

谢一明

(无锡安邦电气股份有限公司,江苏 无锡 214112)

随着现代城市发展，交通拥堵现象日趋严重。为缓解日益拥堵的交通，研究人员从系统角度出发，将众多交叉口进行干线协调控制，同时将众多交叉口的干线协调系统划分成若干控制子区，以取得较好的干线协调、区域协调的控制效果。

杨洁等[1]从路网结构、信号控制方案及交通流离散性对交通子区划分影响的角度，构造路径关联指标，实现交通子区划分；卢凯等[2]基于周期与流量变化关系构造自己的一套计算相邻信号交叉口间关联程度的公式，利用降维处理和遗传算法进行寻优处理，达到快速划分交通路网的目的；梁杰[3]在前人研究车队离散模型的基础上，通过修正离散系数、选取合适的指标对象，将车队离散程度量化，用于中国混合交通子区划分研究；别一鸣等[4]通过梳理前人关于交通子区划分问题的文献，多角度挖掘影响交通子区划分问题的因素，分别从策略层、理论层、算法层考虑交通子区划分问题，形成自己的一套较为系统的交通子区划分策略；别一鸣等[5]专门探究相邻交叉口周期差异对信号交叉口间关联程度的影响，通过提高关联程度计算精度，为交通子区划分提供理论依据；赵伟明等[6]借助synchro软件中的协调因子进行交通子区划分，探究交通子区划分对协调控制的影响。以上研究成果多集中于交叉口间关联程度关系的探讨上，对进入干线协调系统车流量的影响因素把握不准，划分出的交通子区协调控制参数未进行优化标定，且交通控制子区间相位差调整处于盲区，导致预期协调效果与实际协调效果相差较大，协调效果单位周期内不稳定，协调效果不佳。

针对上述研究成果的不足，本文依据系统公共周期调整协调系统内交叉口流量，对整体协调道路网首先依据车流在路段上的散布密度进行初划分；通过分析协调相位绿灯时间内通过车流量的构成及影响因素，利用端点交叉口协调相位绿灯时间对协调道路网进一步划分得到交通子区；对每个交通子区系统周期进行优化，同时对其相位差进行调整；借助双向交通流量关系及绿波带宽关系对交通子区间相位差调整这一难题进行进一步优化，使得双向绿波带宽和最大。

1 交通子区划分

1.1 基于车流散布密度的子区初划分

交通子区划分时需要对各个信号交叉口流量、各相位的绿灯时间、车道宽度、车道数量、停车线间距离等信息进行调查，并依据所调查的流量和车道的饱和流量，借助经典webster法计算各信号交叉口最佳周期时长及各相位绿灯时长。如果所需要协调的道路网全部在同一个交通子区时，可利用下面的公式(3)、(4)求得系统公共周期及各相位的绿灯时长。在周期、协调相位绿灯时长发生变化时需要更新现有周期下调查的流量Qi,i+1，在理想状况下，设定在有效绿灯时间内通过交叉口的流量与有效绿灯时长成正比关系。在更换周期后，协调相位流量变换如下：

(1)

(2)

(3)

(4)

(5)

(6)

在流量发生变化后，整体道路网在同一个交通子区内协调时流量在路段上的散布密度计算公式如下：

(7)

相邻信号交叉口由上行路段与下行路段的双向路段连接，其散布密度计算公式如下：

(8)

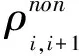
1.2 基于端点交叉口绿灯时间的细划分

协调系统车流运行情形如图1所示。对于协调系统而言，只要速度、相位差、周期三者匹配好，车流在驶经协调系统内交叉口时就不会产生大量的停车排队。协调系统内交叉口协调方向在绿灯时间内依次通过的车流量主要包括4个部分：上个周期绿灯时间内未通过的部分稳定直行流及部分左右转汇入的不稳定流(在本周期变为稳定流)，本周期内由上一个交叉口流下来的稳定直行流部分及本周期内左右转汇入的不稳定流。计算公式如下：

(9)

图1 协调系统车流运行示意图Fig.1 Schematic diagram of vehicle flow operation in coordination system

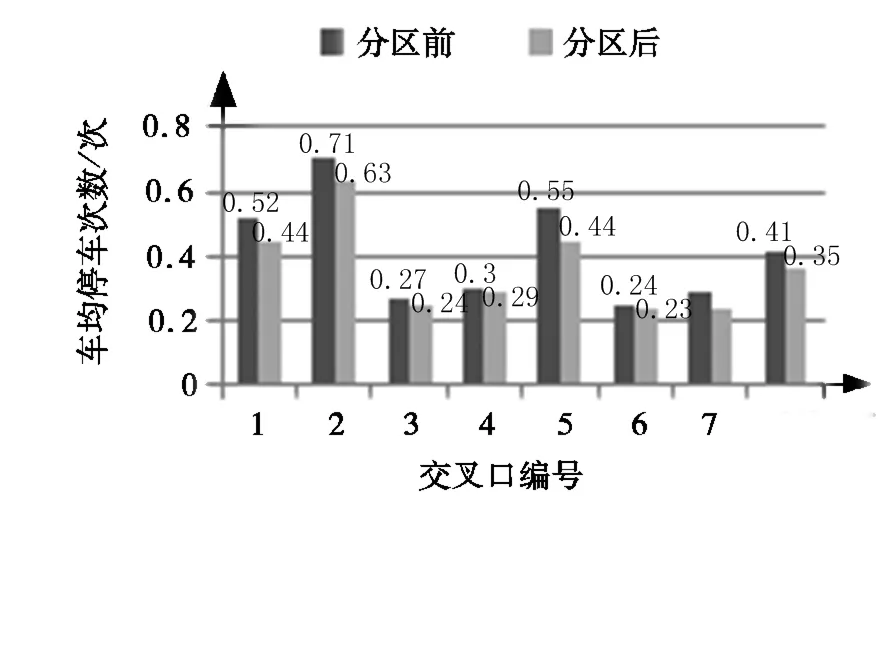
则a2=1；若a1=0，则0a21；若0

(按车流方向依次由小向大标号)

(10)

式中:Sij为协调方向绿灯时长的相似性；gj1、gi1分别是端点交叉口j、i协调方向的绿灯时长，s。由min{Sij}对应的i,j可以将i-j+1个交叉口合并在同一个交通子区。

在某一个交叉口的协调进口道车流来源有稳定直行流与左右转汇入的车流，干线协调主要是以最小成本来满足稳定直行流的交通需求。端点稳定直行流不断降低，左右转汇入的车流随机性加入，必然对稳定直行流的运行状态造成干扰。沿车流方向各个交叉口直行车流由端点交叉口驶入的稳定直行流是逐渐递减的，即沿车流方向各个交叉口的稳定直行流与端点交叉口稳定直行流的关联性逐渐降低，两者比值逐渐减小。

≥η1

(11)

(12)

式中：Qic是交叉口i的超稳定直行流(来源于端点交叉口j的稳定直行流)，pcu/s;Qjc是端点交叉口j的超稳定直行流，pcu/s;η1,η2作为判断阈值根据实际交叉口的交通运行情况给定。

由上可以得出交通子区划分合并的步骤：

Step1：用Webster法求出各个交叉口的最佳周期时长及其各相位的绿灯时间。

Step2：利用式(10)进行寻优搜索，得到合并的交叉口数量及编号。

Step3： 将上述得到的交叉口依次用式(11)、式(12)进行双向检验，不符合约束条件的划分到其它子区。

Step4：合并完成一个子区后，剩下的交叉口以端点交叉口重复Step2、Step3合并交通子区，直到合并完所有交叉口为止。

2 交通子区内系统调整

2.1 系统内求得最优周期

借鉴文献[7]的观点设定每个交叉口的周期时长变化范围是[Ci,o,Ci,o+Li]。

系统公共周期范围选取如下：

Cf=max{[Ci,o,Ci,o+Li]∩

[Ci+1,o,Ci+1,o+Li+1]∩…[Cn,o,Cn,o+Ln]}=

[Cmin,Cmax]

(13)

若Cf不存在时，设定

Cf′=[Cmin,Cmax]=[Cmin,n,Cmax,n]

(14)

公共周期选定：

(15)

其中，Cf是系统公共周期变化范围，s。

2.2 系统内相位差调整

(16)

设li,i+1是交叉口i到i+1方向同侧停车线间的距离(与li+1,i有区别)，m，则上游交叉口的单向相对相位差oi,i+1为：

(17)

为达到双向绿波效果均衡，一般利用公式(18)进行相位差反复调整。

oi,i+1+oi+1,i=nC

(18)

2.3 子区间相位差的调整

因交通流在驶出交通子区时车流离散率很大，且呈车队形式的交通流量减少，直行交通流比重降低，在保证不破坏每个交通子区运行状态的情况下，让头车在进入下一个交通子区前遇到红灯，等待后续车流，在车流重新自行组织后，仍以规律的车队形式驶入下一个交通子区是非常有必要的。因交通子区间的相位差控制与同一个交通子区内交叉口间的控制不同，其相位差调整不能应用公式(18)进行调整优化。本文以双向绿波带宽和最大作为目标，用双向交通流量关系调整交通子区间的相位差，得到最佳控制效果。

maxB=Bs+Bx

(19)

(20)

(21)

(22)

式中：B是双向绿波带宽和，s；Bs是上行绿波带宽时长，s；Bx是下行绿波带宽时长，s；qs是各交叉口上行直行交通量和，pcu/·s；qx是各交叉口上下行直行交通量和，pcu/·s。

3 算例分析

以某干线协调系统为例，各信号交叉口间的位置及距离分布如图2，各交叉口现有周期调查的交通流量及周期见表1。

图2 干线路网示意图(单位：m)Fig.2 Schematic diagram of the main road network

表1 干线系统各交叉口流量及周期Table 1 Flow and cycle of intersections in trunk system

依据上述提出的绿灯时间划分方法进行交通子区划分，具体划分过程及结果如图3。

依据划分出的交通子区，根据本文的相位差优化方法，运用Vissim软件分别仿真分区前后干线协调控制。分区前后各交叉口控制参数对比情况如表2。

采用两相位控制(协调控制相位是东西方向直行车流)，对整个协调路网依据调查情况进行合并，设置合理的饱和流量和信号控制参数及车流速度，仿真3 600 s。提取3 000～3 600 s内车流协调运行结果，选取车均延误时间、车均停车次数作为评价指标进行对比，如图4、图5所示。由图4、图5可知：子区协调控制效果与分区前干线协调控制效果相比，交叉口车均延误降低14.6%，交叉口车均总停车次数减少11.1%，整体协调路网运行效果有所提升；3个端点基准交叉口(2、3、6)控制效果有所改善，车均延误分别下降14.5%、13.9%、12.1%，车均停车次数分别减少10.8%、9.9%、11.8%；7个交叉口中，交叉口1车均延误下降幅度最大(30.8%)，交叉口5车均停车次数下降幅度最大(36.4%)。

图3 交通子区划分流程及结果Fig.3 Flow and result of traffic sub-area division

表2 分区前后各控制参数对比Table 2 Comparison of control parameters before and after the partition s

图4 车均延误Fig.4 average delay

图5 车均停车次数Fig.5 average number of car stops

4 结论

针对传统交通子区划分方法对协调系统中车流运行状态分析不够透彻导致车流量与协调系统公共周期不匹配的缺陷，本文首先将交叉口现有周期内调查的交通流量变为系统周期时进行合理调整，采用车流在协调系统中散布密度进行协调道路网的初级划分；分析协调系统中端点交叉口绿灯时长对协调系统车流量的影响以及相邻交叉口间绿灯时长关系，提出基于端点交叉口绿灯时长的交通子区划分方法；对划分出的交通子区协调提出可行的参数优化方法，并对子区间协调时相位差调整提出合理计算方法；最后选取实例利用Vissim软件对本文方法进行仿真验证。仿真结果表明，本文提出的方法能够进一步提高干线交叉口车辆的通行效率，有力地证明了该理论的正确性。