大规模MIMO-NOMA下行系统可达吞吐量研究

朱翠涛，鲁经纬

(中南民族大学 电子信息工程学院,武汉 430074)

非正交多址接入(NOMA)技术相比于传统的正交多址接入(OMA)技术，能够显著提高系统的频谱效率，是第5代移动通信(5G)关键技术之一.然而，由于NOMA系统中多个用户可共享同一资源块，会产生更多的干扰因素而导致NOMA系统性能下降.为了提高NOMA系统的性能，人们做了大量研究工作.文献[1]证明了在用户随机分布的5G系统中，针对不同用户选取合适传输速率和功率分配因子，NOMA可以获得比传统正交多址更大的系统容量；文献[2]提出了一种基于相关性的用户聚簇算法，分析了迫零预编码和随机预编码在NOMA中的性能，并结合簇内功率分配算法提高了系统和速率；文献[3]和[4]分析并比较了NOMA系统中固定功率分配算法和分数阶发射功率分配算法性能：固定功率分配算法按照固定的比例来分配功率，计算复杂度较低，分数阶发射功率分配考虑了用户信道条件及用户的公平性具有较好的系统性能；文献[5]通过求解NOMA系统总吞吐量最大化问题，分别得出上行和下行的低复杂度用户分簇方案和簇内用户最优功率的闭式解，证明合理的用户分簇和功率分配方法能够提高系统吞吐量；文献[6]基于FDD的大规模MIMO-NOMA系统，先利用统计信道信息对用户分簇，再进行选择构成NOMA用户组，有效降低了簇间和簇内干扰；文献[7]提出一种新型的MIMO-NOMA系统模型，即簇间使用OMA方式，簇内采用NOMA方式，提出一种低复杂度用户分簇算法，然后利用每簇的等效信道增益提出一种新的迫零预编码以消除簇间干扰，并分两步进行功率分配；簇内各用户功率采用文献[5]下行最优功率的闭式解求得，提高了系统的频谱效率.

大规模MIMO与NOMA相结合能进一步提高系统的容量，但随着基站发射天线数的增加，会加剧簇间干扰，从而影响系统的性能.为此，本文针对大规模MIMO -NOMA下行系统的可达吞吐量开展相应研究工作.首先，利用空间相关性提出一种改进的k-means用户分簇算法，将空间相关性较大的用户分为一簇，降低簇间干扰.然后，采用块对角化预编码使各簇之间信道近似正交，进一步消除簇间干扰，并形成了功率约束下的系统可达吞吐量的优化问题模型，通过求解得到最优的用户功率分配系数，提高接收端连续干扰消除(SIC)的可靠性，达到降低簇内用户间干扰的目的.

1 系统与信号模型

单基站多用户FDD下行系统中，设基站配置由N根天线组成的均匀线性阵列，服务K个单天线用户，N>K，将所有用户分为G簇，每簇中有L个用户分布在同一个单散射环内，且同簇用户的信道增益有较大差异，小区内采用基于功率域的非正交多址方式，系统模型如图1所示.

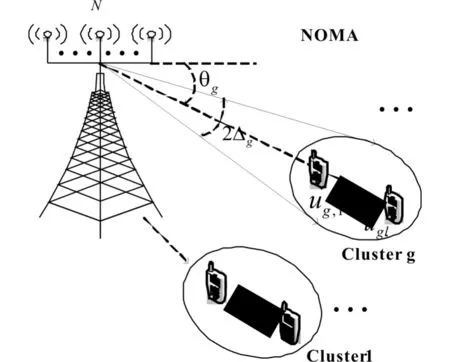
图1 系统模型Fig.1 System model

第g(g∈{1,…，G})簇中用户l(l∈{1,2,…，L})表示为ug,l，其信道向量Hg,l∈1×N可分解为：

(1)

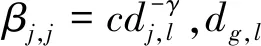
(2)

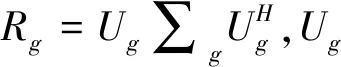
yg,l=Hg,lχ+zg,l=

(3)

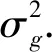
SINRg,l=

(4)

用Wg,l表示归一化的信道增益，且：

(5)

式(5)中，B表示每个发送波束的带宽，则(4)式可简化为：

(6)

用户ug,l可达吞吐量为：

(7)

则系统可达吞吐量表示为：

(8)

由(8)式可知，系统可达吞吐量主要与最优用户分簇方法、预编码以及功率分配方法有关，本文将分别从这三个方面进行研究.

2 联合空间相关性的用户分簇

根据(6)-(8)式可知在一定范围内系统的吞吐量随SINR的增大而增大，合理的用户分簇方法能有效降低簇间干扰，提高用户的SINR.本文提出了一种改进的k-means分簇算法，利用空间相关性对用户分簇.算法的改进包括初始簇中心的选取和迭代分簇两个部分.基本思想为：先采用最大距离法从K个用户中找出G个用户作为初始中心点，然后再采用加权似然准则进行迭代分簇，直到算法达到终止条件.根据用户的空间相关性来划分用户 ，度量用户之间信道特性相似程度的准则如下：

准则1 欧氏距离，欧氏距离函数表达式如下[8]：

(9)

式(9)中，Ug,l是用户ug,l的特征矩阵，Vg为第g个用户簇中心点对应的特征矩阵，D(Ug,l,Vg)≥0，仅当Ug,l=Vg时D(Ug,l,Vg)=0，此时，用户ug,l为第g簇的中心点，‖·‖F表示Frobemius范数.簇用户的中心特征子空间为：

(10)

式(10)中，eig{·}表示求解矩阵的主要特征矢量的运算，每簇传输的数据流数目为Kg.

准则2 加权似然函数[9]

加权似然函数利用各用户的特征向量在各簇中心点的特征向量空间中的投影，将用户划分到不同簇，加权似然值表示为：

(11)

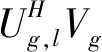
(12)

总的似然值计算式为：

改进的k-means算法具体步骤如下：

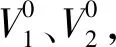
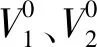
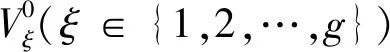
第四步：判断当前簇的个数g+1是否大于等于G，满足则执行第五步，否则重复执行第三步；

第八步：得到分簇结果.

3 簇间预编码

为了进一步消除簇间干扰本文采用块对角化预编码，通过SVD分解，获得每簇相对于其它簇干扰为零的正交基.第g簇总的信道矩阵为Hg=[Hg,1,Hg,2,…,Hg,L]，预编码向量vg需要满足：

Hμvg=0,μ∈{1,2,…,G}且μ≠g,

(13)

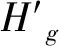
(14)

(15)

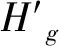
(16)

(17)

即

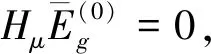
(18)

(19)

4 最优簇内功率分配

本系统模型涉及簇间和簇内两层功率分配.由于各簇用户数目相等，为方便计算，簇间采用等功率分配，若基站发射总功率为Pt，则每簇的总功率为Pt/G.为了保证SIC的性能，降低簇内用户间干扰，最优的簇内功率分配是必要的.

第g簇总功率Pg=Pt/G，簇内各用户离基站的距离满足dg,1Wg,2>…>Wg,L，根据NOMA功率分配原则，信道条件好的用户应分配较低的功率，信道条件差的分配较高的功率，因此簇内各用户的功率分配系数需要满足αg,1<αg,2<…<αg,L.此外，各用户功率之间还需满足保证接收端SIC性能的约束条件[5]：

(20)

(21)

式(21)中，第一个约束条件是指簇内功率分配系数之和不大于1，第二个约束条件表示每个用户的传输速率必须大于最低速率r0，此外，簇内各用户功率之间要存在一定的差值，即要满足第三个约束条件.分析上述优化问题可知，该优化问题为非凸问题，本文利用KKT条件进行求解.由拉格朗日函数可得：

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

根据(27)-(28)式解得当每簇用户数目分别为2,3,4时簇内用户的功率分配系数，如表1所示，得到的功率分配系数需要满足式(29)-(30).

表1 每簇用户数为2,3,4时对应的最优功率分配系数

Tab.1 Optimal transmission power allocation coefficient for 2-,3-,and 4-users in each cluster

每簇用户数目最优功率分配系数L=2αg,1=12-τ2Wg,lαg,2=12+τ2Wg,lL=3αg,1=14-τ2Wg,1+τ4Wg,2()αg,2=14+τ2Wg,1-τ4Wg,2αg,3=12+τ2Wg,1L=4αg,1=18-τ2Wg,1-τ4Wg,2-τ8Wg,3αg,2=18+τ2Wg,1-τ4Wg,2-τ8Wg,3αg,3=14+τ2Wg,2-τ4Wg,3αg,4=12+τ2Wg,3

当簇内有L个用户时，由数学归纳法得到各用户的功率分配系数为：

(31)

由等式(31)两边同类项系数对应相等可得：

ζl-1Wg,l-2,l=3,4,

分析优化问题的约束方程及求解过程可知，每簇有L个用户时，求解时有2L个拉格朗日乘子，满足KKT条件的组合方式有22L种，但是本文的优化变量为用户的功率分配系数满足αg,l∈[0,1]，l∈{1,2,…，L}，当有L个优化变量时，只需L个方程来求解，所以22L种组合方式不必全部验证，通过对每簇2,3,4个用户的情况求解可知，KKT条件个数依次为2,4,8个，由数学归纳法可得簇内L个用户的组合方式为2L-1种.

5 实验与分析

本系统模型中基站配置均匀线性天线阵列，天线间距为，用户天线数为1，用户均匀分布在的扇区内，单环散射模型的角度扩展为，其它参数设置如下表2：

表2 仿真参数配置Tab.2 Simulation parameters

比较改进k-means算法与传统k-means的收敛性能，阈值ε=0.01，K=15,G=3，中心角依次为θ1=-45°，θ2=0° ，θ3=45°，角度扩展Δ=10°，假设簇与簇之间不重叠，当前后两次迭代总的似然值之差DΓtot小于阈值时，算法收敛.两种分簇算法的收敛性能如图2所示，横坐标为迭代次数，纵坐标为DΓtot的值，两种算法都能快速达到收敛，但改进k-means算法收敛更快，只需6次迭代就达到收敛，传统k-means需要16次才能收敛.另外，改进的k-means算法选取的各簇中心点之间距离较远，使得用户簇之间相关性更弱，更有利于降低簇间干扰.

图2 收敛性能比较Fig.2 Comparison of convergence performance

对本文分簇算法与随机分簇、按用户信道状态排序分簇算法[5]进行性能仿真和比较.当总用户数为15，使用不同算法将用户分为3个簇，簇间使用块对角化预编码，接收端采用SIC接收信号.

系统可达吞吐量随信噪比变化规律如图3所示.所提算法减弱了簇间的相关性，降低了簇间干扰，从图3中可以看出，系统可达吞吐量性能最优，而且低信噪比时吞吐量性能较好，其次是按用户信道状态排序分簇算法，分簇时利用了用户间信道条件的差异，但未充分考虑簇间的相关性，随机分簇系统性能最差，主要原因是随机分簇没有考虑用户自身的信道条件，具有随机性，系统的吞吐量得不到保证.

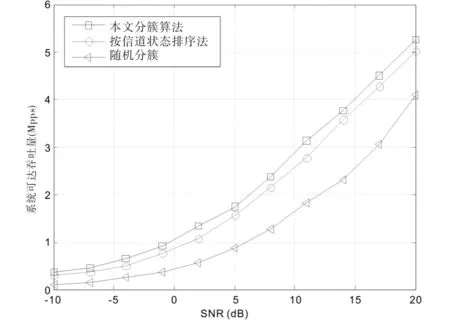
图3 不同分簇算法下系统可达吞吐量比较Fig.3 Comparison of achievable throughput by different clustering algorithm versus SNR

为研究簇内功率分配对系统可达吞吐量的影响，将本文最优功率分配算法与固定功率分配、分数阶发射功率分配进行仿真和比较.先用改进k-means算法分簇，并用块对角化对发送信息做预处理，接收端采用SIC.

设固定功率分配因子为0.1，分数阶发射功率分配因子为0.7，仿真结果如图4所示.

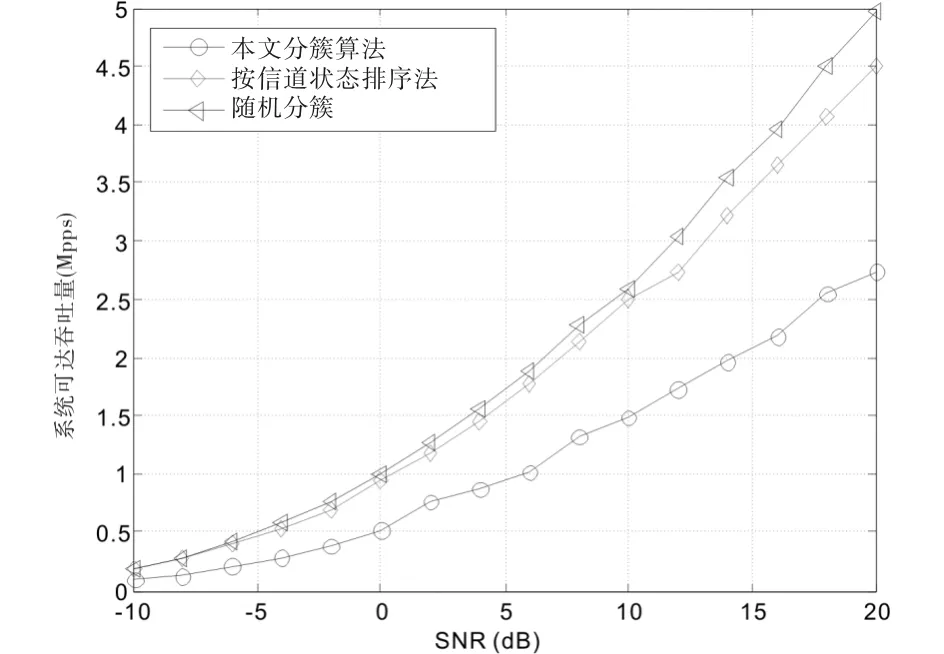
图4 不同功率分配方法对系统可达吞吐量的性能比较Fig.4 Comparison of achievable throughput by different power allocation algorithm versus SNR

低信噪比时本文算法吞吐量性能与分数发射阶功率分配很接近，前者略高，随着信噪比的增大，本文算法优于分数阶发射功率分配算法，而固定功率分配系统可达吞吐量较低.由此看出，固定功率分配算法虽实现复杂度低，但系统吞吐量性能较差，分数阶发射功率分配相比于固定功率分配吞吐量性能更好，本文的功率分配算法满足最小传输速率和SIC性能约束条件，能有效保证每个用户的服务质量，并且降低用户间干扰，提高低信干噪比用户的信号质量，从而提高系统的吞吐量，在三种方法中性能最优.

6 结语

为了提高大规模MIMO-NOMA下行系统的可达吞吐量，本文依据空间相关性提出改进的k-means算法对用户分簇以降低簇间干扰，然后采用块对角化预编码对各簇信息进行预处理，进而消除簇间干扰，并利用KKT条件求解簇内最优功率分配问题，得到簇内各用户最优功率分配系数，提高了接收端SIC性能，降低簇内用户间干扰，仿真结果表明本文的方法提高了系统的可达吞吐量.但是，随着用户数的增加，k-means分簇算法的复杂度也会随之增大，下一步研究将对分簇算法进一步优化.