具有载荷扰动抑制的卫星姿态控制方法及验证

李明群，雷拥军，* ，牟小刚

1.北京控制工程研究所，北京 100190

2.空间智能控制技术重点实验室，北京 100190

随着空间任务需求的不断增长，卫星将要承载的有效载荷种类越来越多，其中有很大一部分载荷在正常工作时需要保持旋转，如海洋水色仪、扫描微波辐射计、微波散射计、微波成像仪、扫描镜等。旋转的载荷将会给卫星姿态带来干扰［1-10］，若不进行干扰补偿，则卫星姿态稳定度和指向精度都会下降，影响卫星的任务，这种干扰严重时甚至会激发挠性附件(如太阳翼)的振动，导致卫星的姿态震荡。为此需要研究具有针对旋转载荷的扰动抑制的卫星姿态控制方法。

刘蕊等［1］分析了载荷扫描镜运动与翼板步进运动对卫星姿态的影响。王新民等［2］分析了载荷干扰力矩的特性及对卫星姿态的影响，说明了周期波动的干扰力矩必将导致姿态的周期波动。张庆君等［5］主要从微振动方面进行研究，从微振动的传递路径设计、振动源抑制、降低载荷敏感性等方面介绍了微振动抑制方法。于哲峰等［6］针对扫镜运动对卫星姿态的影响作了分析和仿真;雷静等［7-8］采用特征系统实现算法对扫描运动的干扰进行估计。王雪冰等［9-10］设计了基于干扰观测器对卫星干扰力矩进行估计，并加以前馈补偿。Liu［11］将周期干扰基波的幅值参数作为状态量，设计了状态观测器对干扰力矩进行估计，并做前馈补偿。

本文利用李亚普诺夫方法，在反馈通道设计了基于参数辨识的自适应控制算法，该算法可确保干扰力矩的参数未知情况下闭环系统稳定，并实现干扰力矩的估计和补偿。本文最后利用真实卫星的控制部件展开了物理试验验证。

1 星体动力学及载荷扰动描述

对于一类带有绕星体固定轴周期转动大型载荷航天器，由于动、静不平衡特性的存在，载荷转动时会对星体产生相应的扰动力矩。将卫星中心体视为刚体，考虑载荷运动扰动的卫星动力学方程可表示为:

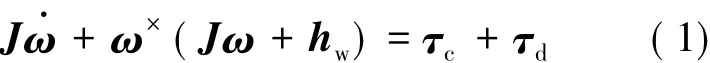
式中:ω为卫星角速度;J为星体转动惯量，为正定对称阵;hw为角动量交换装置的合成角动量;τc为姿态控制力矩;τd为载荷运动时对星体产生的干扰力矩;(·)×表示对应向量形成的反对称矩阵。

由载荷运动的周期性，其产生的扰动力矩可表示为:

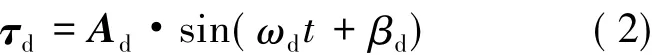
式中:Ad为扰动力矩幅值;ωd为载荷运动角频率;βd为扰动力矩的相位。

式(2)所示扰动力矩可进一步表示为:

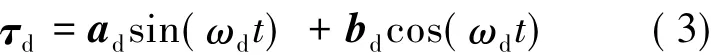
式中:ad、bd为常系数。

2 具有扰动抑制的姿态控制

2．1 载荷周期干扰的影响分析

在对地稳定运行时，星体相对轨道坐标系的姿态可采用欧拉角参数描述，记星体三轴欧拉姿态角分别为φ、θ与ψ，通常称之为滚动角、俯仰角和偏航角，对应的星体角速度ω可表示为:

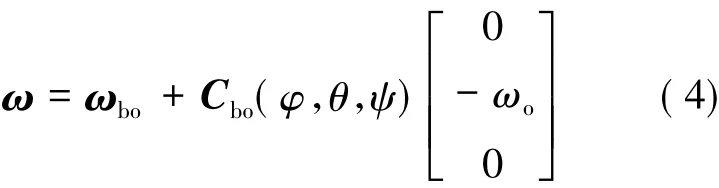
式中:ωbo为星体相对轨道系的角速度;Cbo为星体系相对轨道系的方向余弦阵;ωo为轨道角速率，对于近圆轨道可近似看作为常数。

当三轴姿态φ，θ，ψ为小量时，ωbo可近似表示为且有

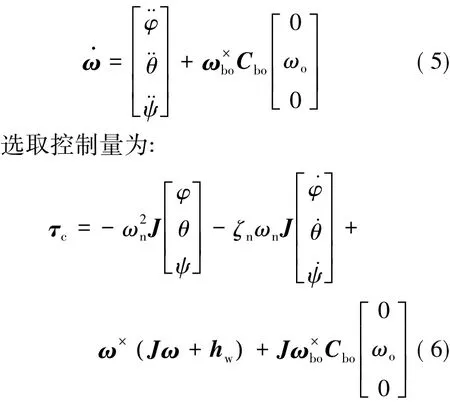
式中:ωn、ζn＞0为选取的控制参数，其决定闭环系统动态特性，可按各通道控制性能要求进行设计。为了描述简洁，本文中给出3通道对应变量参数均为相同。

在式(6)所示控制下，由式(3)与式(1)可得闭环系统的动力学方程为:

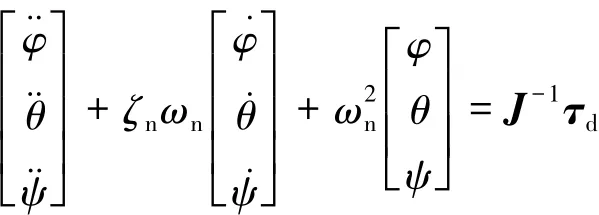
由上可知，在载荷有界扰动下系统姿态将存在偏差。

2．2 具有扰动估计的自适应控制律设计

在式(3)所示扰动力矩基础上考虑系统常值扰动cd，式(3)改写为:

于是式(1)表示为:

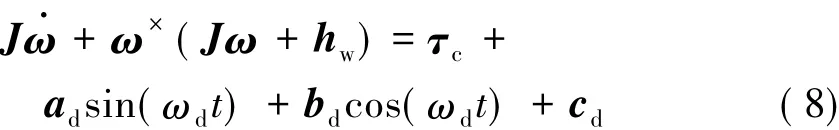
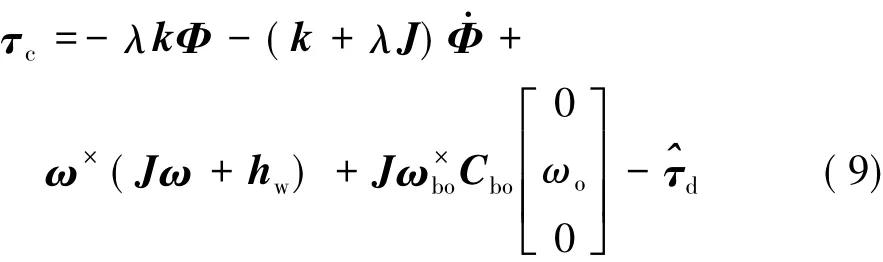
式中:^ad、^bd与 ^cd分别为ad、bd与cd对应的估计值，相应的参数自适应律为:

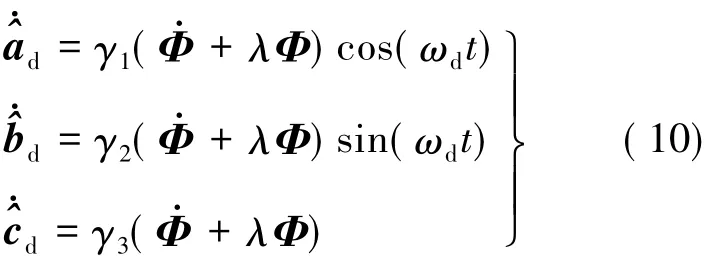
式中:参数更新增益 γ1、γ2、γ3为大于零的常数。

2．3 系统的稳定性分析

将式(9)代入式(8)，有

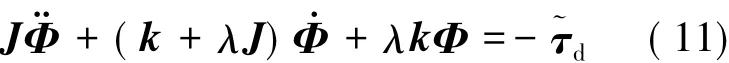
针对式(8)与参数自适应律式(10)组成的闭环系统，以下采用李亚谱诺夫稳定性直接分析方法对系统稳定性进行分析［12］。

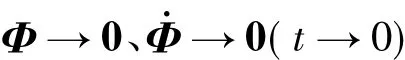
综上可得闭环系统稳定，其中姿态角及姿态速度角误差趋于零，且估计扰动力矩参数^ad、^bd与^cd均有界。

3 物理试验

本文所述的干扰力矩补偿方法在气浮台进行了试验验证，鉴于负载质量和惯量较大，非水平姿态条件下会对驱动机构产生较大的影响，因此本文试验采用单轴气浮台试验，则本文算法的公式中可不考虑轨道角速度ωo。

3．1 单轴气浮台试验系统

试验系统如图1所示，由单轴气浮台、台上仿真控制系统、地面控制台等组成。其中台上仿真控制系统的控制部件、计算机、载荷均为星上真实设备。

高精度单轴气浮台主要由气浮轴承、仪表平台和测角装置组成。仪表平台台面直径为2．2m，转动惯量 450 kg·m2，台体扰动力矩小于0．002N·m，台体测角装置绝对位置精度优于1″，测角分辨率优于 0．2″，角速度精度可优于0．0001(°)/s。

图1 单轴气浮台试验系统Fig.1 Single axis air-bearing table

载荷转动惯量 140 kg·m2，标称转速为45(°)/s，平台配置一个动量轮作为执行机构。星上软件驱用动量轮产生与载荷角动量大小相等、方向相反的角动量，对载荷角动量进行抵消，保持整个气浮台的零动量，同时以台体的姿态角和角速度作为反馈量，采用PD控制方法对卫星平台进行姿态控制，控制周期为0．25s。

3．2 试验结果

(1)无干扰力矩补偿

当载荷稳定在标称转速旋转时，由于动不平衡、静不平衡、以及转速不稳定的影响，会对平台产生干扰，图2为载荷的实际转速。

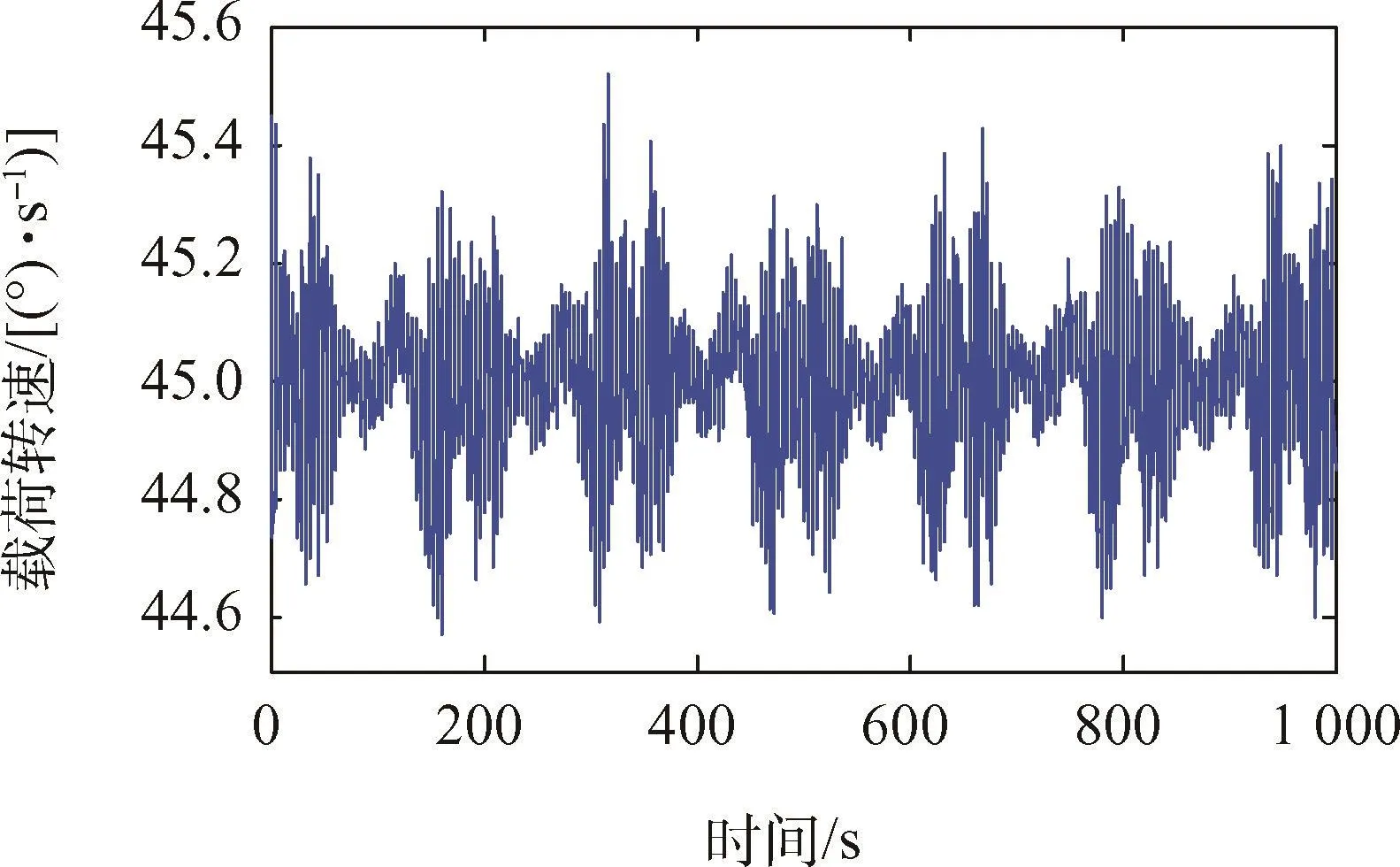
图2 载荷的转速Fig.2 Speed rotor of load

在不进行干扰力矩补偿的情况下，PD控制器的控制参数选择为 kp=10．24、kd=122．93，得到平台的角度及角速度曲线如图3、图4所示。

对角速度的频谱分析如图5所示。

可以看出，在不做干扰力矩补偿时，转台角速度主要集中在0．125Hz频率上，说明在这个频率上存在较大的干扰力矩，这恰好与载荷旋转的频率相同，其他几个次要的频率分量都是载荷转速的0．5倍频、2倍频、3倍频，这就说明转台所受的干扰力矩主要与载荷旋转相关。

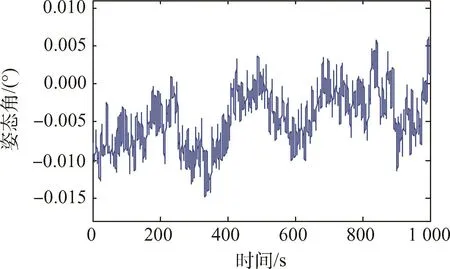
图3 无干扰力矩补偿的姿态角Fig.3 Attitude angular without interference suppression

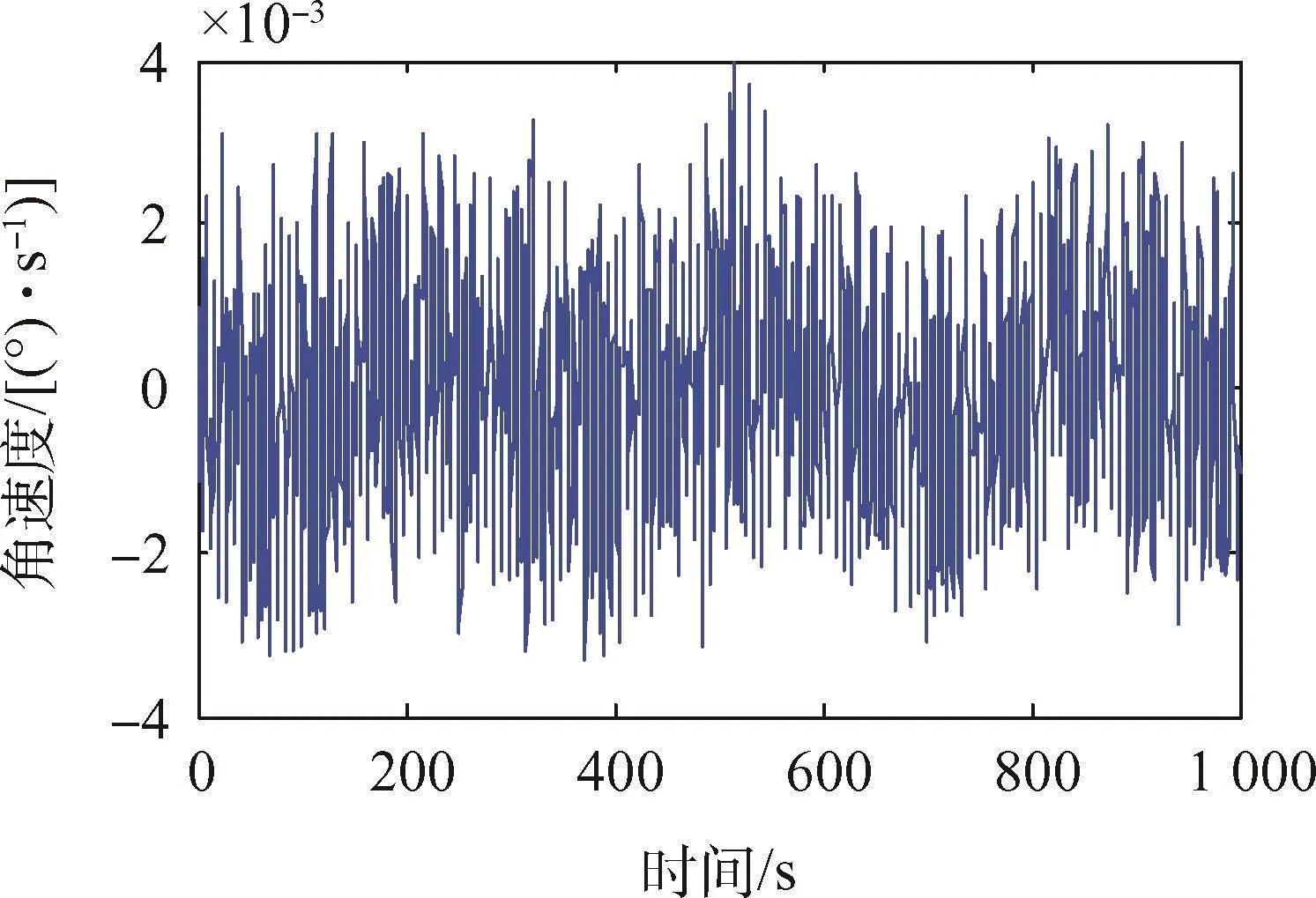
图4 无干扰力矩补偿的角速度Fig.4 Attitude angular rate without interference suppression

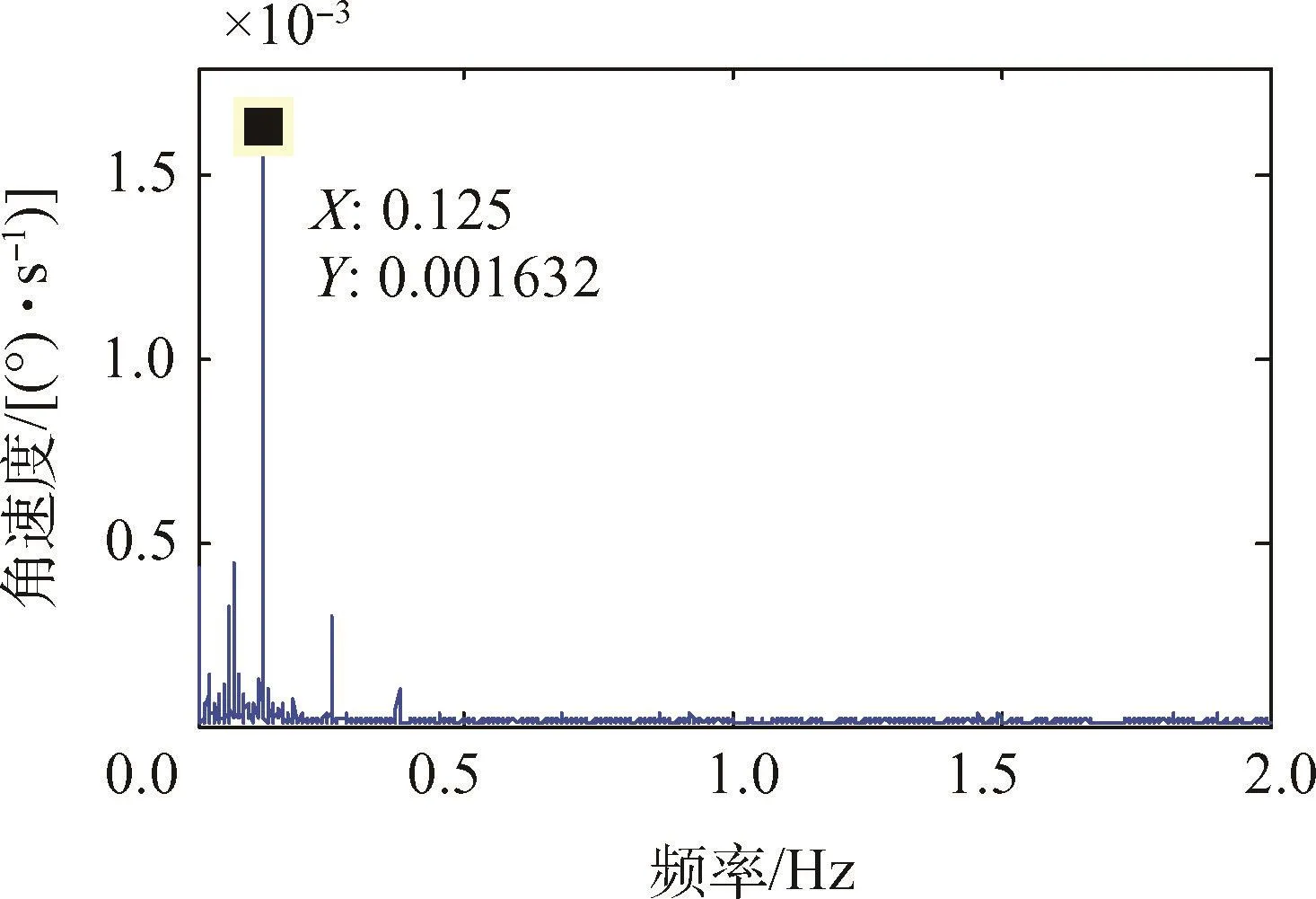
图5 无干扰力矩补偿的角速度频谱Fig.5 Frequency spectrum of attitude angular rate without interference suppressio

(2)基于参数辨识的自适应控制

根据频谱分析，选择载荷旋转的频率，即选择0．125Hz为干扰力矩估值的频率，利用第2．2节式(9)(10)描述的自适应控制率，设置参数kp=10．24、kd=122．93、λ =0．05、γ1=100、γ2=100、γ3=100，控制效果如图 6、图 7 所示。

对比图2、图3和图6、图7，可以看出自适应控制提高了姿态角控制精度、减小了角速度。对转台角速度作频谱分析如图8所示。

对比图5和图8，可以看出经过自适应控制算法得干扰力矩补偿，角速度在0．125Hz的分量被有效的抑制，说明该算法对干扰力矩辨识准确，补偿有效。

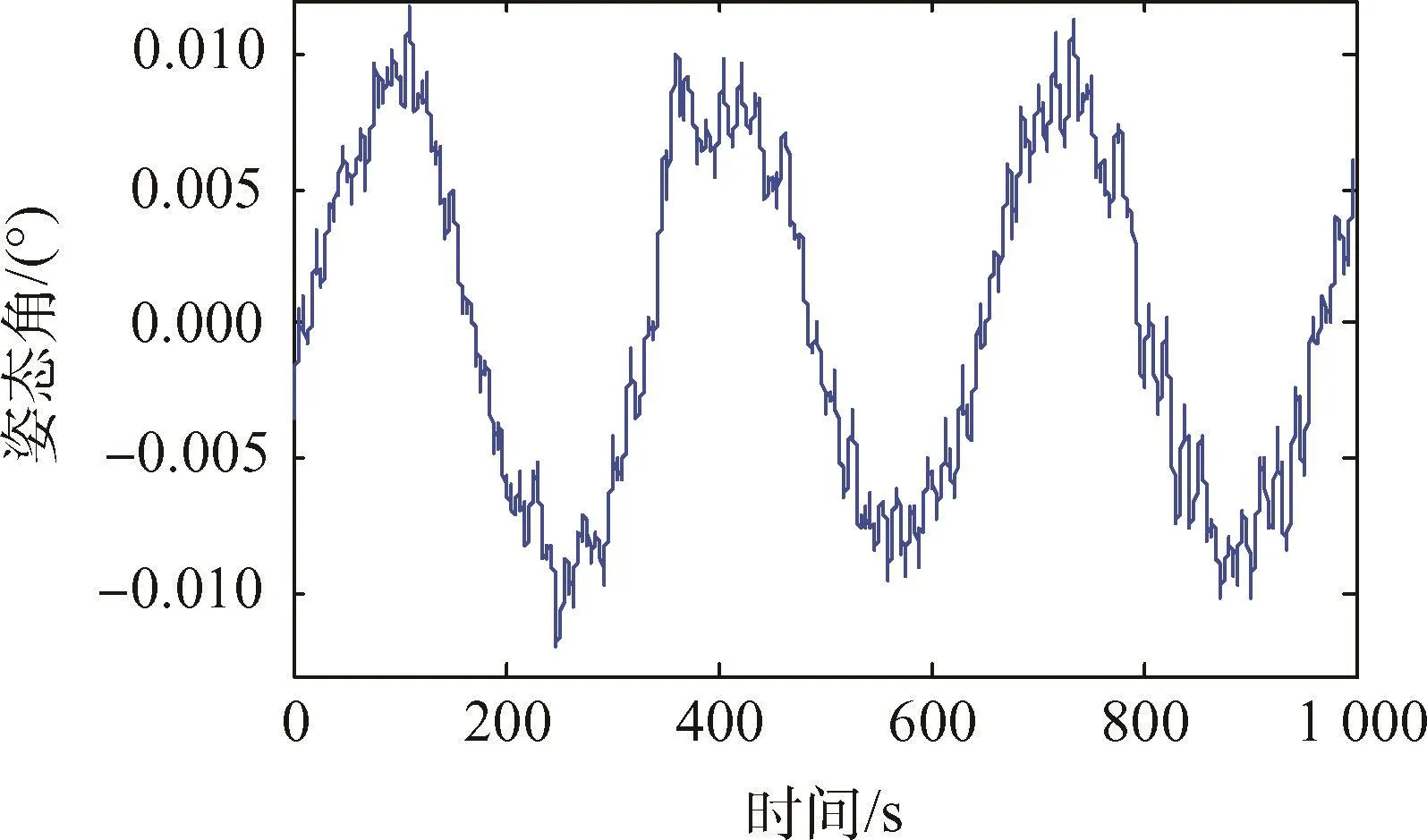
图6 自适应控制的姿态角Fig.6 Attitude angular with adaptive control

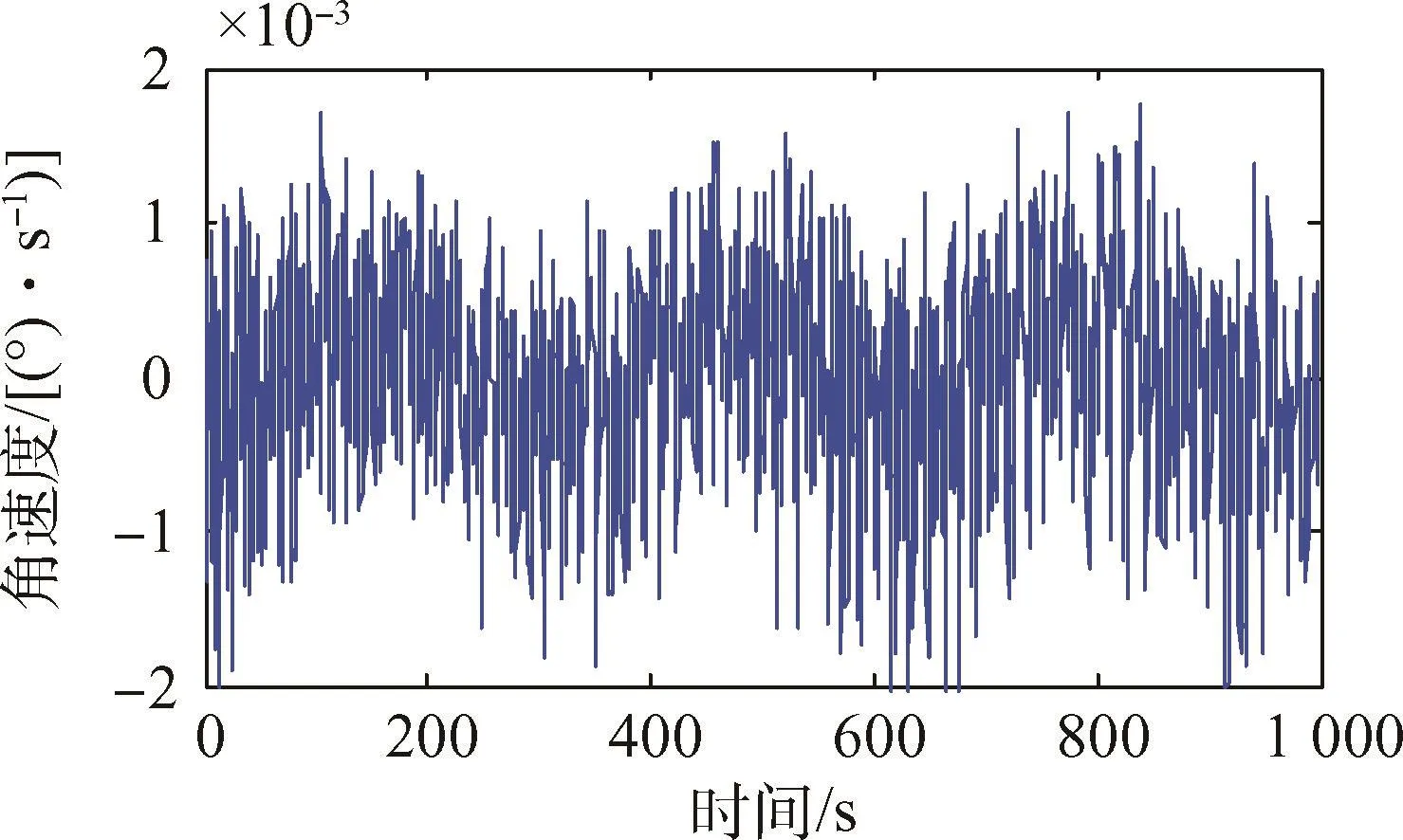
图7 自适应控制的角速度Fig.7 Attitude angular rate with adaptive control

图8 自适应控制的角速度频谱Fig.8 Frequency spectrum of attitude angular rate with adaptive control

4 结束语

本文研究了卫星姿态控制中对旋转载荷产生的干扰的抑制问题，针对干扰的周期特性，设计了对干扰进行参数辨识的自适应控制方法。本文最后利用真实的卫星控制部件，基于单轴气浮台作了物理试验验证，通过控制效果的比较及频谱分析，表明本文的方法对干扰进行了正确的估计和补偿，具有明显的干扰抑制作用，且本文算法的形式简单，易于星上软件实现，有较好的应用前景。