视深度和视侧移问题的再探讨
夏思寒
(中国科学技术大学物理学院,安徽 合肥 230022)
笔者拜读二文[1,2],原文作者对关于从空气中观察水中的物体时的视深度和视侧移问题通过尺规规范作图进行了探讨,笔者读后颇受启发,但感觉原文笔力未尽,故对原问题作进一步的探讨如下.
为了使问题的探讨更全面,下文分两种情形,一种为从空气(光疏介质)中观察水(光密介质)中的物体情形,即“鸟看鱼”情形;另一种为从水(光密介质)中观察空气(光疏介质)中的物体情形,即“鱼看鸟”情形.
1 “鸟看鱼”情形
1.1 “鸟看鱼”的视深度
假设鱼儿位于水面下h深处,鸟在水面上方观察,若视线与水面法线的角度为θ,如图1所示.令水的折射率为n,取空气的折射率为1.为了讨论的方便,将鱼视为点,图1中用点S表示鱼,用点S′表示鸟看到的“鱼”,即鱼的像.在鸟的视线方向取一微小张角为dθ,根据折射定律有

图1
nsinr=sinθ,
所以ncosrdr=cosθdθ,

从图中可以看出P、Q间的距离可表示为
PQ=h[tan(r+dr)-tanr]=
h′[tan(θ+dθ)-tanθ].
由上式可得视深h′为


代入、化简并整理得
(1)
此式即为鸟看鱼的视深度的表达式,式中θ∈[0,90°].

1.2 “鸟看鱼”的视侧移
另外,由图1可知像向观察者所在一侧偏移,设像的侧移为ΔL,则


(2)
此式即为鸟看鱼的视侧移的表达式,式中θ∈[0,90°].

结论:鸟从水面上方观察水中鱼,看到的“鱼”(像)的位置在鱼(物)的上方且偏向观察者,上移和侧移的大小与观察者观察的视线方向有关,视线与水面法线的夹角越大,上移和侧移越大;视线与水面法线的夹角越小,上移和侧移越小.
2 “鱼看鸟”情形
2.1 “鱼看鸟”的视深度
假设鸟儿位于水面上方h深处,鱼在水面下观察,若视线与水面法线的角度为α,如图2所示.仍令水的折射率为n,取空气的折射率为1.为了讨论的方便,将鸟视为点,图2中用点S表示鸟,用点S′表示鱼看到的“鸟”,即鸟的像.在鱼的视线方向取一微小张角为dα,根据折射定律有
sinβ=nsinα.
所以cosβdβ=ncosαdα.


图2
从图中可以看出M、N间的距离可表示为
MN=h[tan(β+dβ)-tanβ]=
h′[tan(α+dα)-tanα].
由上式可得视深h′为


(3)


2.2 “鱼看鸟”的视侧移
另外,由图2可知,像向远离观察者的一侧偏移,设像的侧移为ΔL,则
ΔL=h′tanα-htanβ=

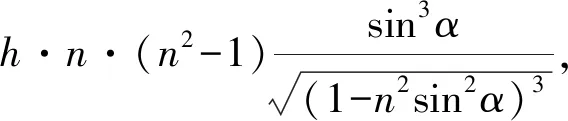
(4)

结论:人从水面上方观察水中鱼,看到的“鱼”(即像)的位置在鱼(即物)的上方且偏向观察者,上移和侧移的大小与观察者观察的视线方向有关,视线与水面法线的夹角越大,上移和侧移越大;视线与水面法线的夹角越小,上移和侧移越小.
综上所述可知,由于光的折射,观察者从光疏介质中观察光密介质中的物体时,会感觉物体的位置比实际位置浅些、近些.而从光密介质中观察光疏介质中的物体时,会感觉物体的位置比实际位置高些、远些.

