基于Matlab电磁聚焦的动力学仿真
程 琳,翟立朋
(1.西安工程大学 理学院,陕西 西安 710048;2.西安交通大学 理学院,陕西 西安 710049)
在大学物理实验中磁聚焦法常常被用来测量电子的比荷[1]. 电子的比荷是电子最基本的属性,也是重要的物理学常量,其测量在近代物理学的发展历史中具有重大意义,电子的比荷非常小,到目前为止还没有直接测量的方法,所以常常需要借助电子在电磁场中的运动来进行测量,如磁聚焦法、汤姆逊法、滤速器法和磁控法等. 同时,磁聚焦方法除了被用于测量电子的比荷,也可以用来测量地球磁场[2],在工程上也有广泛的应用. 电子束的磁聚焦,一般是将阴极发射的热电子,先经过加速电场后再经过磁场和交变电场偏转,最后达到聚焦的目的. 单个电子的运动非常容易理解,但是一系列电子的行为往往不太容易理解聚焦具体是如何形成的[3],并且大部分文献中关于磁聚焦原理的阐述都关注于电子在磁场中的运动[4-6],虽然给出过可视化的磁聚焦模型[7],但对电子在偏转电场中的运动阐述较少. 本文通过数值方法,基于电子在电磁场中的动力学模型,最终计算出电子位置随时间的变化关系,直观地仿真出电子在电磁场中的运动,构建带电粒子在电场和磁场中的可视化的运动模型,有助于理解带电粒子在复杂电磁场中的运动.
1 电磁聚焦的基本原理
以电子显像管为例说明磁聚焦原理,如图1所示,电子显像管有直流加速、交流偏转和直流励磁3个重要的区域. 图1中的轨迹描述的是单个电子在显像管中的运动轨迹.
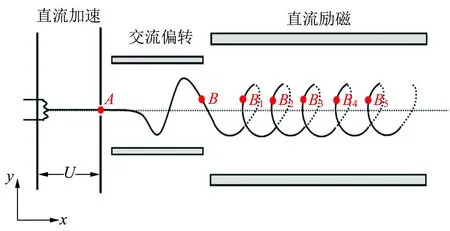
图1 显像管的构造
热激发产生的电子初速度一般都比较小,在经过直流加速区后,会获得如图1所示x轴方向上的速度. 假设加速电压为U,则经过直流加速区后电子的速度vx满足
(1)
则电子在达到如图1所示的A点时,在x轴方向
上产生的速度可以表示为
(2)
电子以vx的速度经过A点后,进入交流偏转电场,由于上下2个极板之间的正负属性一直在不间断地发生变化,所以在y轴方向上电子将会做相间的分段加速、减速运动,从而电子在y轴方向上会产生振荡,而x轴方向由于没有力的作用,将会一直做匀速直线运动. 由于电子束中不同的电子进入交流偏转电场的时刻不同,所以在y轴方向上的偏转方向和角度就会产生差别,此时电子束会被发散,使得不同的电子在y轴方向上产生的分速度vy也不同,但是由于水平方向上所有电子的运动是一致的,都是匀速直线运动,所以最终会在1个周期之后,聚焦到点B处. 所以电场也有电子聚焦的功能和效应,偏转电场的目标就是把电子聚焦到B处,使B处具有不同方向不同角度射出的电子.
如果将电子在B点的速度分解为水平方向上的vx和竖直方向上的vy,则电子在通过A点后,vx一直保持不变,而vy则随着交变电场的变化而一直不间断在做周期性变化,直到B点,vy大小取决于偏转电压的大小和周期,但是对后续磁聚焦并没有定量影响,所以不做定量讨论. 电子在经过B点之后,由于具有x轴方向的磁感应强度B和y轴方向上的速度,所以在垂直与x轴的yz平面上电子将做匀速率圆周运动,在x轴上依然以vx的速度做匀速直线运动,这样电子在磁场中就可以做如图1所示的直流励磁部分的螺旋运动.
在磁场中洛伦兹力提供电子运动的向心力,所以有
(3)
由(3)式可得到电子做圆周运动的半径和周期为
(4)
(5)
电子通过B点后经过1个周期T到达B1点,此时和B点相比因为圆周运动经过了1个周期回到原处,而水平方向沿x轴平移h距离,即
(6)
将(2)式代入(6)式,可以得到
(7)
由(7)式可以看出,电子每经过1个周期就会沿着x轴平移h,距离h为螺旋运动的螺距. 通过(7)式可以看出电子的螺距与电子的质量m、电荷e、加速电场U、磁感应强度B有关,所以在实际实验测试中,只要测试设备的参量给定,螺距就是常量,同时在yz平面内电子的圆周运动半径R只与vy有关. 所以对于1束电子束而言,所有电子的h相同但R不同,所以电子束在经过B时会由于R不同而发散开,到B1点时又由于h相同而聚焦,这样就形成了磁聚焦的效果. 在实验中如果能测得螺距h,则可以根据(7)式计算电子的比荷,即
(8)
其中B为载流长直螺线管产生的磁感应强度,螺线管中轴线上产生的磁感应强度可表示为
(9)
其中Is为螺线管中的励磁电流,N为螺线管的线圈匝数,L为螺线管的长度,P为螺线管的直径. 将(9)式代入(8)式可以得到电子的比荷为
(10)
这样即可得到电子的比荷.
2 电磁聚焦的动力学仿真模型
为了更清楚地描绘电子在电磁场聚焦中的具体运动情况,本文基于Matlab将电子运动的动力学方程在时间维度离散迭代,将电子运动的轨迹可视化,这样更有利于理解磁聚焦的模型.
从t=0时刻开始,在时间维度以间隔Δt对时间进行等分,如果时间间隔Δt足够小,则任意时刻都可以表示为
t=NΔt.
(11)
其中N为任意1个整数,所以,只要能表示出任何时刻电子所受的作用力F(t),由牛顿运动定律就可以表示出电子运动的加速度,即
(12)
因为前面假设了时间间隔Δt足够小,所以电子在t到t+Δt之间的运动看作是匀变速直线运动,加速度a(t)可以从(12)式得到,如果已知t时刻电子的运动速度为v(t),则t+Δt时刻电子的速度就可以表示为
v(t+Δt)=v(t)+a(t)Δt.
(13)
同理,如果已知t时刻电子所处的位置为r(t),那么在t+Δt时刻电子的位置就可以表示为
(14)
从t到t+Δt时间也可以用匀速直线运动公式计算,只要是时间间隔Δt足够小,结果就可以保证足够精确. 同时,如果期望描述电子在三维空间的运动,直接将(13)式和(14)式分别写成x,y,z方向上的速度和位移即可. 所以,只要知道某一时刻电子所处的初始速度和初始位移,时间以Δt为间隔进行迭代,就可以求得后续任意时刻电子运动的速度和位移. 原则上,只要Δt足够小,迭代结果也将足够精确.
根据以上离散的动力学模型,在Matlab中按照如图2所示的具体流程进行仿真计算.

图2 动力学仿真模型
先从变量初始化开始,动力学计算过程中,需要的变量有作用力F、加速度a、速度v和位移r,变量设好以后,给定电子运动的初始条件为
r(0)=0,
v(0)=0,
进入循环之后因为偏转电压随时间改变,导致加速度a、速度v和位移r都会随着时间的迭代而产生改变. 这样,随着时间的迭代,就可以描述出电子运动的位移和速度等物理量.
从图2的迭代模型可以看出,该动力学模型本质上不局限于电磁聚焦问题,而是可以拓展. 只要能够表示出物体所受的力F,并且该物体的运动符合牛顿运动定律,就可以对物体运动进行动力学仿真,所以这种离散的动力学仿真方法可以被广泛应用到物体运动中.
3 电磁聚焦的结果与讨论
根据上述离散的动力学模型,先计算带电粒子在偏转电场中的情况. 在此假设交变电场以U=U0cos (2πft)的形式变化,图3所示为8个电子在交变偏转电场中的运动轨迹,不同颜色的轨迹代表不同的电子. 从图3中可以看出:1)每个粒子的运动轨迹都是正弦(或余弦)轨迹,但由于每个电子进入交变电场中的时间都不一致,有的电子刚入电场就开始向上偏转,而有的电子刚入电场则向下偏转,所以导致电子轨迹在刚进入电场的A点开始发散,反映到轨迹的函数表达式上,这体现在轨迹函数表达式的初相位不同;2)不管电子如何发散,运动轨迹每过1个周期都会聚焦1次,如图3所示,电子运动的轨迹分别聚焦在B,C,D,E点处;3)聚焦点的连线与x轴有一定的夹角,这是因为电子进入交变电场中的时间并不是恰好在交变电场相位为零时进入电场. 所以,只需要在电子经过任意一聚焦点之后进入磁场即可确保进入磁场的电子是从同一位置发出的,并且在y轴方向具有不同的入射速度vy,从而满足磁聚焦需要的条件. 所以,通过仿真可以清楚地看到,原本经过加速电场后的电子只具有x轴方向的初速度,而交变电场的目标就是为了使电子在进入磁场之前具有y轴方向的速度.

图3 电子在电场中的聚焦
电子在通过图1所示的B点后,就进入方向沿着x轴的匀强磁场(本文没有考虑螺线管轴线上的磁场变化). 之后电子因为受洛伦兹力的作用在yz平面做圆周运动,因为经过电场偏转以后,不同粒子在y方向的速度vy不同导致圆周运动的半径不同,但所有的螺旋运动都会聚焦到点B1,B2,B3,B4. 图4所示为8个电子在磁场中的运动轨迹,清晰地描述了电子在磁场中的聚焦. 与电场聚焦不同的是,磁场中聚焦的连线是平行于x轴分布.

图4 电子在磁场中的聚焦
实际电磁聚焦过程中,热电子是可以连续不间断地进入磁场,所以电子的运动轨迹远远大于图4所模拟的8条. 如果增加电子个数,就会形成如图5所示的一系列电子连续不断进入磁场中进行聚焦的行为轨迹,即一系列半径不同的螺旋轨迹. 如果逆着x轴方向观察,在聚焦点的位置,荧光屏上观察到的是1个点,这就是大学物理实验中观察到的最直观的磁聚焦现象.

图5 电子束在磁场中的聚焦
如果荧光屏位于除聚焦点之外的其他位置上,相当于电子束没有聚焦,这时如果逆着x轴方向观察,则会看到1条线段,荧光屏所处位置不同,线段的长度和方向也不相同. 图6所示为荧光屏位置x处于0~h之间的不同位置处,所观察到的电子束的情况. 位置从0增大到螺距h的过程中,电子束在荧光屏上逐渐从1个点扩展为线段,并且线段的长度先增大后减小,线段的方位角也一直不停地变化,方位角是顺时针变化还是逆时针变化取决于螺线管中磁感应强度的方向,当x=h时线段缩短为1个点, 与x=0的状态重合,即经过了1个周期. 有关线段长短的定量分析在文献[8]中有详细的论述. 图6所示的现象也是在磁聚焦法测电子比荷实验中调节聚焦点时直观观察到的现象.

图6 位于x轴方向不同位置处观察到yz平面内电子束
4 结束语
电磁聚焦是常用的测量电子比荷的方法,本文基于Matlab对电子在电磁场中的聚焦行为进行动力学仿真分析,形象直观地阐述了电磁聚焦的行为过程. 可视化的仿真分析,可以让学生更好地理解电磁聚焦的过程,并且将动力学仿真的方法拓展到所有符合牛顿运动定律的运动研究.

