由多边形小孔的远场衍射解释灯光的星芒
陈耿剑,周新宇,何春清,王晓峰
(武汉大学 a.物理科学与技术学院; b.物理国家级实验教学示范中心,湖北 武汉 430072)
在晚上看远处的路灯时,能看到许多星芒从灯芯射出. 当倾斜观察时,星芒在视界中的位置不变,这说明星芒的产生源于眼睛,或者说星芒的出现与眼睛的结构有关. 当光圈较小时用相机拍摄亦有类似现象. 图1给出了人眼与相机镜头的光学结构,各部分一一对应:角膜—物镜,瞳孔—光圈,晶状体—目镜,视网膜—感光元件(图1中未标出). 可以看出,人眼具有与相机相似的光学结构,为了解释与人眼有关的光学现象,不妨先以相机为例进行研究. 图2为Cannon相机(镜头参量:EF-S 18-55mm 1:3.5-5.6 IS STM,φ58 mm,光圈7叶)所拍摄的约40 m外的路灯的星芒. 其他参量不变的情况下调整光圈值由F6.5到F16,星芒由“光刺”变为“光柱”,人眼观察到的情形为二者混合.

图1 人眼与相机镜头

(a) F6.5光圈下的 (b) F16光圈下的 “光刺”状星芒 “光柱”状星芒图2 40 m外路灯的星芒(相机拍摄)
图3为镜头光圈与人眼瞳孔的对比[1],两者近似为正多边形的小孔,推测星芒现象可能源于光在多边形小孔的边缘发生了衍射. 接下来从光的衍射理论出发,结合数值模拟与实验给出星芒数量规律,并尝试精确计算星芒的位置和亮度.

图3 镜头光圈与人眼瞳孔
1 理论分析
设物距为d1,物光波U(x0,y0),物透镜组焦距为f,物光波经过多边形衍射孔(光圈或瞳孔)后变为U1(x0,y0)[2],则
(1)
其中,λ为光波波长,k是波数.
球面波在光圈处发生衍射,为了计算在d2处接收屏上的波前U(x,y),将U1代入菲涅耳衍射公式[3],
U(x,y)=C∬t(x0,y0)U(x0,y0)·
(2)
其中C为复数,|C|为常量. 特别是当
亦即满足几何成像关系时,(2)式化为
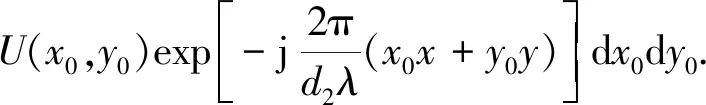
(3)
即在像平面的波前U(x,y)为U(x0,y0)的傅里叶变换. 在目镜透镜组的作用下,在像平面处得到夫琅禾费衍射图样最终成像在相机的感光元件或视网膜上.
2 数值模拟
单缝的远场衍射可得到解析解,对于形状复杂的小孔难于得到解析解,但利用快速傅里叶变换,可方便地计算出任意形状小孔的衍射图样. 将d2记为d,令
x=pΔx,y=qΔy,x0=mΔx0,y0=nΔy0,
并取
为傅里叶变换的频率变量,将U0(mΔx0,nΔy0)简记为二维数组U0(m,n),得
U(p,q)=DFT (U0(m,n)),
(4)
式中,U0(m,n)表示衍射前的波前,U(p,q)表示衍射后的波前. 还可推出当衍射屏的取样宽度为L0且取样数为N时,接收屏的宽度为[4]
(5)
普通光源为复色光,是多个非相干单色光的叠加. 考虑单色光,计算距离为d=8 870 mm的衍射图样,利用(5)式,可得在衍射屏宽度为L0=12.28 mm,N=512,λ=632.8 nm时,衍射图样宽度L=233.87 mm. 图4为正四至正八边形孔的衍射图样. 计算结果表明:如果正多边形小孔边数n为偶数,衍射产生的光刺有n条;如果n为奇数,则光刺为2n条.
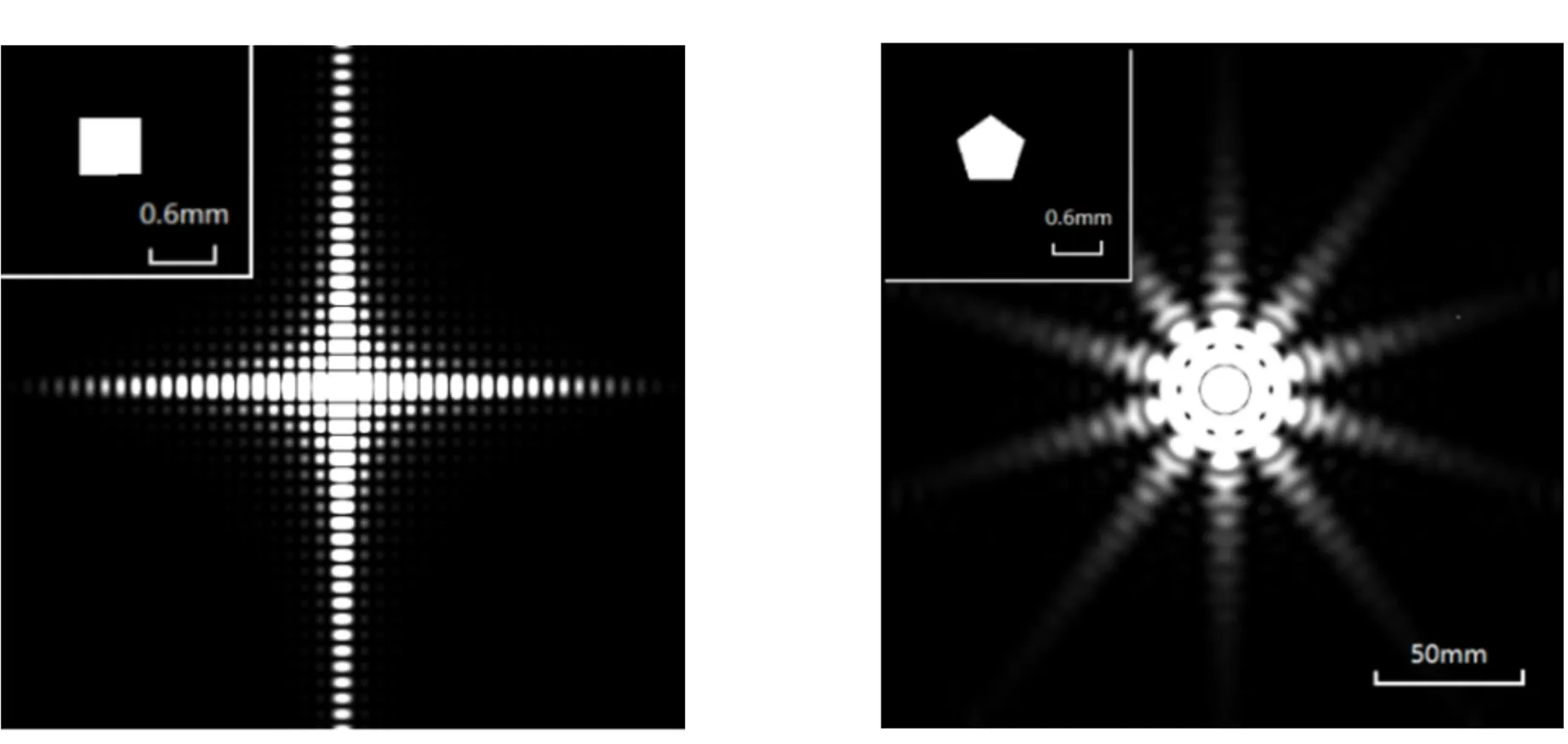
(a)正方形孔 (b)正五边形孔
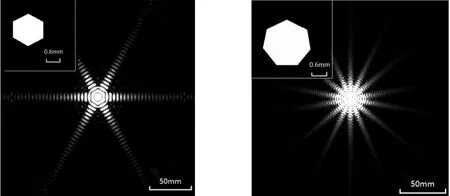
(c)正六边形孔 (d)正七边形孔

(e)正八边形孔图4 正多边形孔的模拟衍射图样
图5为正三角形孔和曲边三角形孔的衍射图样. 从图5中可以看出,如果多边形的边有一定曲率,衍射后的“光刺”会钝化为“光柱”,这解释了图2中相机用不同大小光圈拍摄远处路灯所产生的现象.

(a)正三角形孔 (b)曲边三角形孔图5 正三角形孔及曲边三角形孔的衍射图样
数值计算中可以进一步综合考虑光源的多色、非点光源等性质. 不同波长光之间不相干,它们在感光元件或视网膜上的衍射图样会简单叠加. 根据(5)式,其他参量相同但光波长不同,衍射图样的大小不同. 扩展光源上不同点发出的光线也不满足空间相干条件,在感光元件或视网膜上的衍射图样只相差平移变换. 据此可以以扩展光源每个几何像点为中心,按照光源色谱权重分别生成多个衍射图样后,在RGB编码方案中计算各个衍射图样叠加. 最终的计算结果与图2中现象类似. 计算机模拟正七边形孔的衍射图样如图6所示.

图6 计算机模拟正七边形孔的衍射图样
3 实验验证
用实验室常用的衍射屏进行了初步实验. 如图7所示,衍射屏中正三角形孔和正方形孔的边长均为0.2 mm,这远小于手机后置摄像头的通光孔径(手机摄像头不存在可调大小的物理光圈),因此用手机紧贴衍射屏拍摄数米远处的LED闪光灯可得到与(3)式对应的衍射图样. 拍摄得到的衍射图样与数值计算的图4和图5中对应正多边形孔的衍射图样相符. 对于更多边形的孔只能采用手工制备或购买特定叶数光阑的方式,因为加工精度的原因多边形孔的尺寸与手机摄像头通光孔径相当,不适合用上述方式进行实验. 同时用复色光不便于进行理论与实验对比,因此采用了激光(单色性好、强度高)入射且远场接收的方式进行实验,以便于得到定量数据与理论进行对比.

(a)正三角形孔 (b)正方形孔 图7 白光的正三角形孔与正方形孔衍射图样 (附图中微尺总长度为1 mm)
如图8所示,用氦氖激光器(波长632.8 nm)作为光源,将激光照射在带有多边形小孔的衍射屏上,在8.87 m远的接收屏处观察衍射图样. 受限制于实验室没有长焦距的透镜和实验室空间等诸多条件,无法直接测得无穷远处的夫琅禾费衍射图样,但是远场处的衍射图样可以近似描绘出无穷远处的夫琅禾费衍射图样的特点. 实验中使激光器水平放置,调整衍射屏的高度使激光束恰好覆盖小孔,同时调整接收屏的位置以便观察. 用单反相机拍摄干涉条纹图样,用笔在接收屏上描出0级斑的中心和各级明亮条纹的中心. 用刻度尺测量亮条纹中心到0级衍射斑中心的距离,并将拍得衍射图样导入Matlab计算条纹亮度.

图8 实验光路图
实验中采用的衍射屏为:正三角形孔、正方形孔、在纸上剪裁出正五边形孔、在纸上剪裁并且结合刀片截出的正六边形以及正八边形光阑. 此处未加入正七边形孔的实验结果是因为正七边形孔不易于裁剪. 图9为实验中所用的多边形小孔及其衍射图样. 从实验结果可以看出:当多边形孔的边数n为奇数时,星芒有2n条;n为偶数时,星芒有n条. 这验证了理论部分关于星芒数和孔边数的结论. 图9中正五边形小孔衍射图样与图4中理论计算结果有差别,这是因为手工裁剪的五边形并非严格的正五边形,并且孔较大,不严格满足远场条件[5].
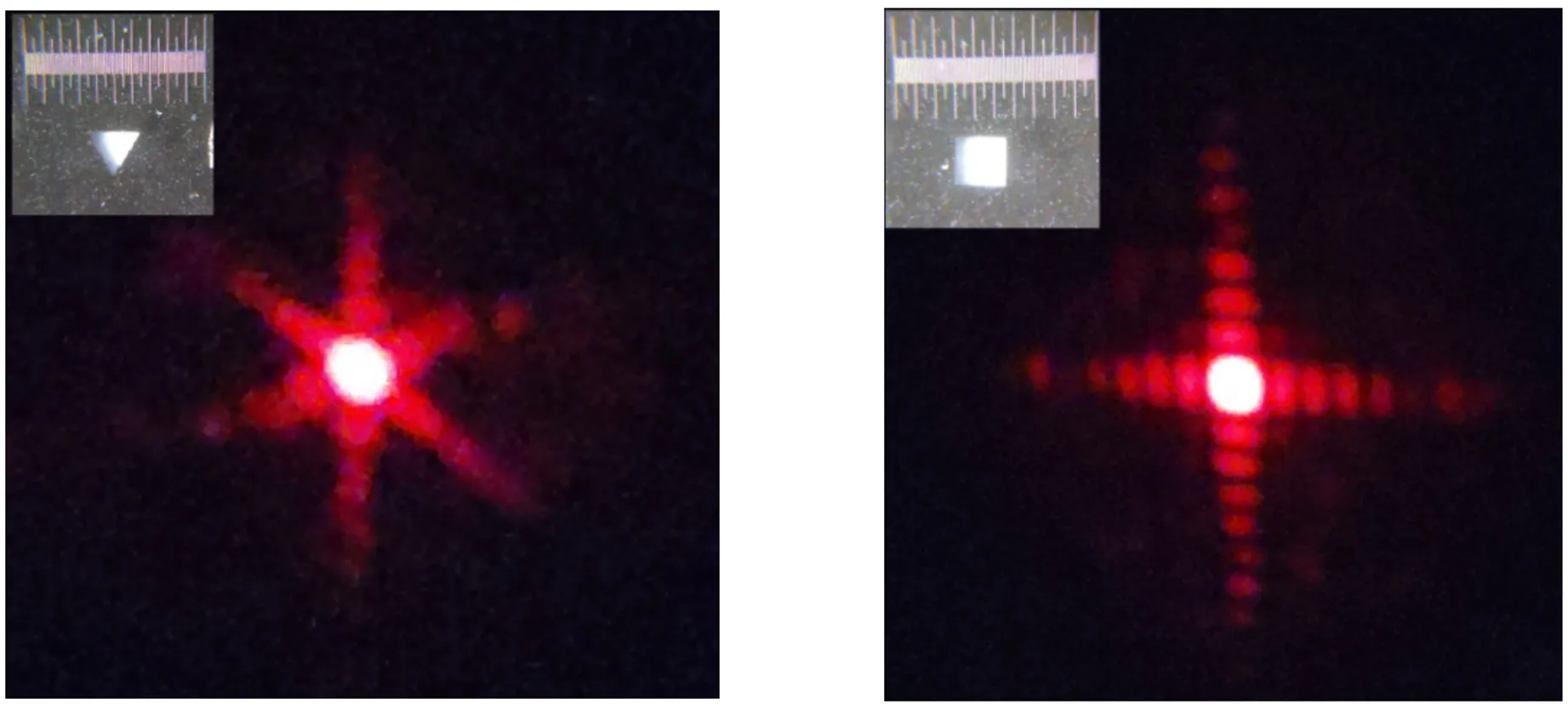
(a)三角形 (b)矩形

(c)五边形 (d)六边形

(e)八边形图9 多边形小孔及其衍射条纹(附图中钢尺最 小刻度为1 mm)
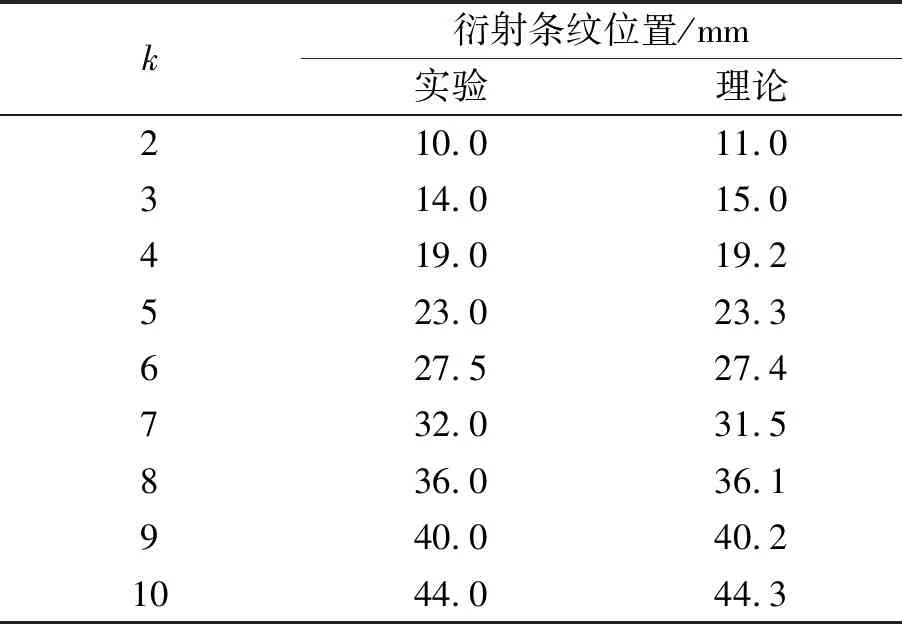
表1 六边形孔不同级次衍射条纹到中心距离的实验与理论对比
利用Matlab自带函数rgb2gray,将实验拍摄的彩色图片转换成灰度图与理论计算进行对比,如图10所示,可以看出实际相对亮度和理论相对亮度在观察屏所在的平面上具有相似的分布.

(a)实际相对亮度 (b)理论相对亮度图10 六边形小孔衍射图样的亮度
图11为六边形孔衍射图样沿1对星芒方向实验测量和理论计算的亮度对比,在感光元件的线性感光区间,理论计算和实验测量符合得较好. 当光强过强时,相机的感光单元会产生大量外溢的电子,因此1级条纹与0级斑不太容易分辨. 当光强太弱时,相机的感光效果与实际亮度是非线性变化的,因此弱光区的实验测量结果和理论预测的结果相比略微偏大.
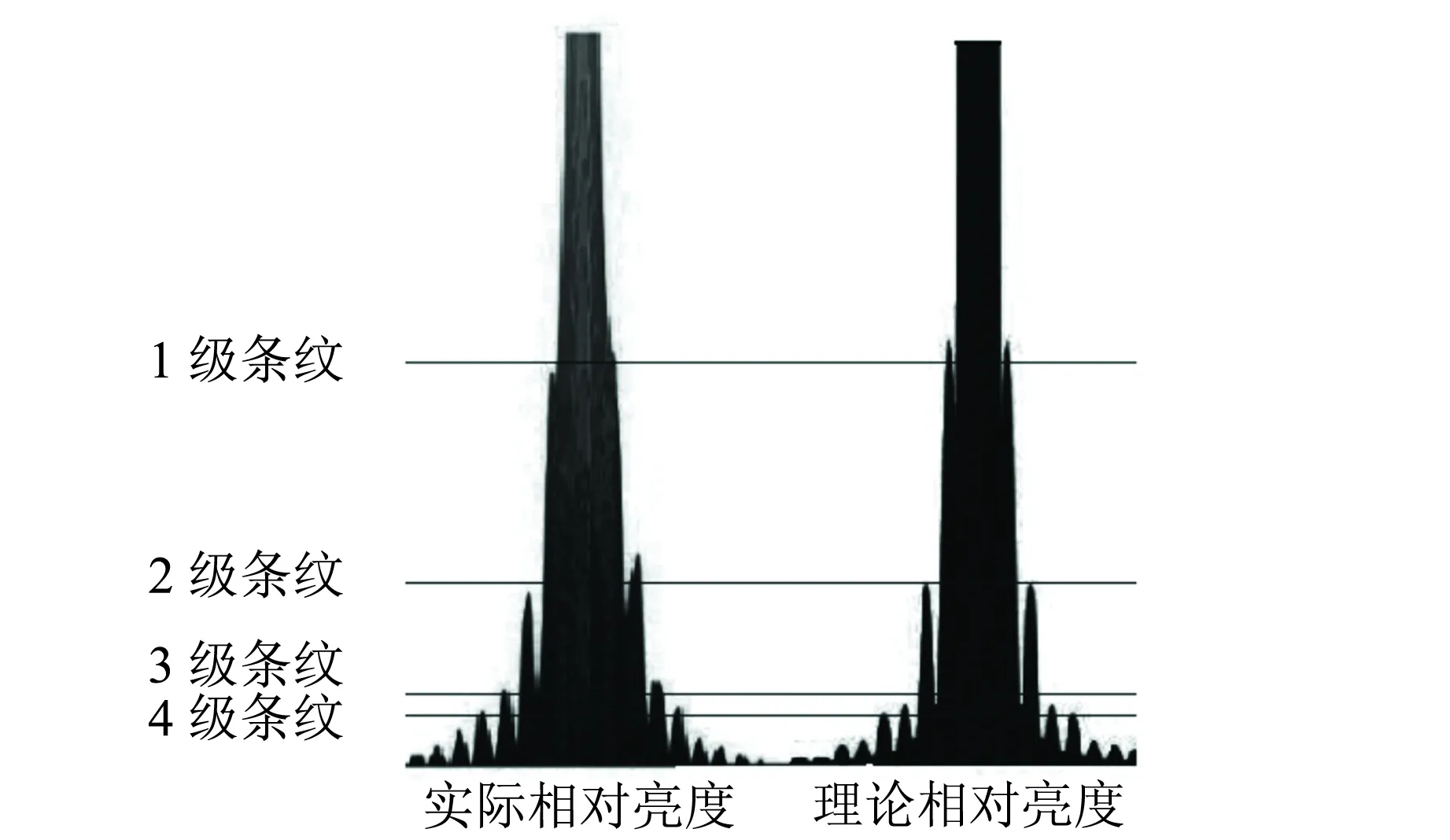
图11 六边形孔衍射图样中1对星芒 方向的实验和理论亮度对比
4 应 用
瞳孔并不是规则的圆形或正多边形,它的边缘有许多“坑坑洼洼”,因此用肉眼观察远处的灯光时,会看到许多光刺和光柱从灯芯射出. 这些缺陷一般情况是均匀分布的,然而部分人的瞳孔有巨大的先天性缺陷,他们能看到某一方向的衍射光芒非常强烈. 利用此特性,可以检查瞳孔是否有先天性缺陷.
5 结 论
用光的衍射理论证实了相机感光元件记录的图样为光圈的远场衍射图样, 揭示了星芒的成因.由数值计算可得:当多边形衍射孔的边数n为
奇数时,星芒有2n条;n为偶数时,星芒有n条. 若光圈的边为直线,则衍射图样为“光刺”;若光圈的边为带有一定曲率的圆弧,则衍射图样为“光柱”. 综合考虑光源的多色、非点光源等性质模拟了实际生活中观察到的现象. 设计实验观察了正三、四、五、六、八边形孔的远场衍射图样. 对于正六边形孔,衍射条纹到中心的距离、各级衍射条纹的相对亮度的实验结果与理论结果符合,说明了理论分析的正确性和数值算法的有效性.

