压电式快速反射镜系统建模与传递函数辨识
陆金磊,姜晓明,王 军
(1.南京理工大学 先进发射协同创新中心,江苏 南京 210094; 2.上海机电工程研究所,上海 201109)
0 引言
压电式快速反射镜(PFSM)采用压电叠堆作为驱动器[1],具有体积小、响应快、精度高、动态性能好等优点,在自适应光学[2]、图像稳定系统[3-4]、目标跟踪系统[5-6]、生物医学系统[7]等领域具有广泛的应用前景。本文将PFSM应用在光电精密跟踪系统中,将其作为复合轴子系统的执行机构,主要用于校正机架主系统的随机误差。为稳定跟踪目标,光电跟瞄系统的精度需要达到微弧度级,这对PFSM的控制精度提出了很高要求。对于控制设计者来说,如何获得被控对象的精准数学模型极为关键。
目前,常用的传递函数参数辨识方法主要包括时域阶跃响应法和频域频率响应法。蔡骞等[8]采用阶跃响应法对摆式倾斜仪传递函数进行了辨识,该方法测试方便,但只能将系统近似为低阶系统,精度较差。在频率响应辨识法中,常用的有曲线直接辨识和函数拟合辨识。刘金星等[9]结合测量得到的伺服系统开环Bode图和自动控制原理,通过理论计算直接得出PFSM系统的传递函数,该方法较为简单直观,但误差较大。黄海波等[10]采用最小二乘法辨识出复合轴精跟踪系统的传递函数,该方法操作方便,辨识精度较高。
本文根据压电叠堆材料的特性和反射镜的运动机理,构建了PFSM系统传递函数模型,并结合实测的PFSM系统幅频和相频响应特性,使用非线性最小二乘曲线拟合法,选定合适的迭代初值,针对不同频率特性进行分段拟合,得到了精确的PFSM系统传递函数,为控制器设计奠定了基础。
1 PFSM系统建模
PFSM系统主要由控制器、模数和数模(AD&DA)转换模块、功率驱动模块、PFSM和电阻应变片传感器构成,如图1所示。图中:电阻应变片传感器检测到压电叠堆的位移量电压信号,依次经过滤波器、传感器放大模块和AD转换模块输入到控制器。电阻应变片传感器模块的传递函数可用一个比例环节描述;功率驱动模块采用线性功率运放直接驱动,具有很好的线性特性,其传递函数也可用一个比例环节描述;在忽略频率混叠效应后,AD转换的传递函数为1/T,T为采样周期;DA转换可被看作一个零阶保持器,其传递函数为(1-e-Ts)/s。在后续的辨识过程中,可人为去除AD&DA过程对结果的影响。因此,在分析中,可不考虑AD&DA环节。

图1 PFSM系统控制框图Fig.1 Block diagram of PFSM system control
以下根据PFSM的运行机理,构建其传递函数模型。文中的PFSM采用Physik Instrumente公司的S340偏转头,该偏转头由四压电叠堆驱动。当电压施加在压电叠堆上时,压电叠堆产生逆压电效应,每对压电叠堆形成推拉运动,驱动镜面转动。图2为四压电叠堆的反射镜俯视图。图中:A,B,C,D分别为4个压电叠堆,沿圆周呈90°垂直分布;镜面中心与致动器和反射镜接触点的距离为r;BD轴为俯仰轴;AC轴为方位轴;θa为方位角;θp为俯仰角。设压电叠堆的传递函数为G1(s),PFSM机械运动的传递函数为G2(s),则PFSM的传递函数可表示为
G(s)=G1(s)G2(s)
(1)

图2 四压电叠堆的反射镜Fig.2 Fast steering mirror driven by four piezoelectric stacks
压电叠堆是将单个晶片做得很薄,然后将数百片叠加起来,从而实现机械上的串联和电路中的并联。可以将压电叠堆等效成一个电容来进行分析,如图3所示。
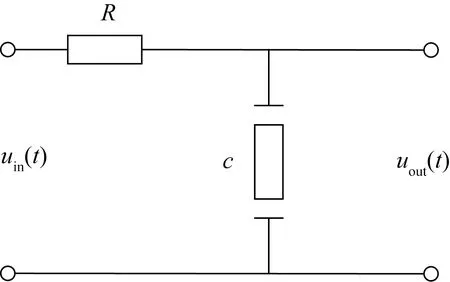
图3 压电叠堆等效模型Fig.3 Equivalent model of piezoelectric stack
图中:t为时间;uin(t)为电源电压;uout(t)为施加在压电叠堆上的电压;R为电源的输出电阻;c为压电叠堆的等效电容。根据基尔霍夫电压定律可得
(2)
对式(2)进行拉普拉斯变化,设初始条件为0,可得
Uin(s)=RcsUout(s)+Uout(s)
(3)
令τ=Rc为时间常数,则压电叠堆的传递函数为
(4)
根据压电叠堆运动特性,建立机构简化模型,如图4所示。

图4 机构简化模型Fig.4 Simplified model of mechanism
图中:F为压电叠堆输出驱动力;Kf为阻尼系数;Kg为连接刚度;x为压电叠堆变形量。设反射镜质量为m,则压电叠堆机械运动的数学模型可用微分方程描述为
(5)
根据压电叠堆的变形特性,压电叠堆输出驱动力F与压电叠堆变形量x之间的关系为
F=Kp(auo(t)-x)
(6)
式中:Kp为压电叠堆等效刚度系数;a为待定系数。
将式(6)代入式(5),整理得
(7)
对式(7)进行拉普拉斯变换,设初始条件为0,则可得到PFSM机械运动传递函数为
(8)
结合式(4),(8),可得PFSM传递函数为
GPFSM(s)=G1(s)G2(s)=
(9)
由式(9)可见,PFSM的传递函数为一个惯性环节和一个二阶振荡环节(也可能是过阻尼的)的串联,可表示为
(10)
式中:a0,bi(i=0,1,2)即为要辨识的参数。因功率放大环节和电阻应变片传感器的传递函数都可被看作比例环节,故这2个比例环节的系数也可包含在参数a0,bi中。事实上,由于PFSM的机械刚度有限,因此系统的开环特性往往在高频段附加一个或多个如式(11)所示的双二阶的机械谐振环节[11],
(11)
式中:bi(i=3,4,5,6)即为要辨识的参数。根据以上分析,PFSM系统的开环传递函数可被看作式(10)和一个或多个式(11)的串联。
2 PFSM系统数学模型辨识
使用动态信号分析仪,产生的线性扫频信号为
(12)
式中:A为振幅;f0为初始频率;k为频率随时间增加的斜率。用此信号,可以获得PFSM系统的频率特性,如图5所示。
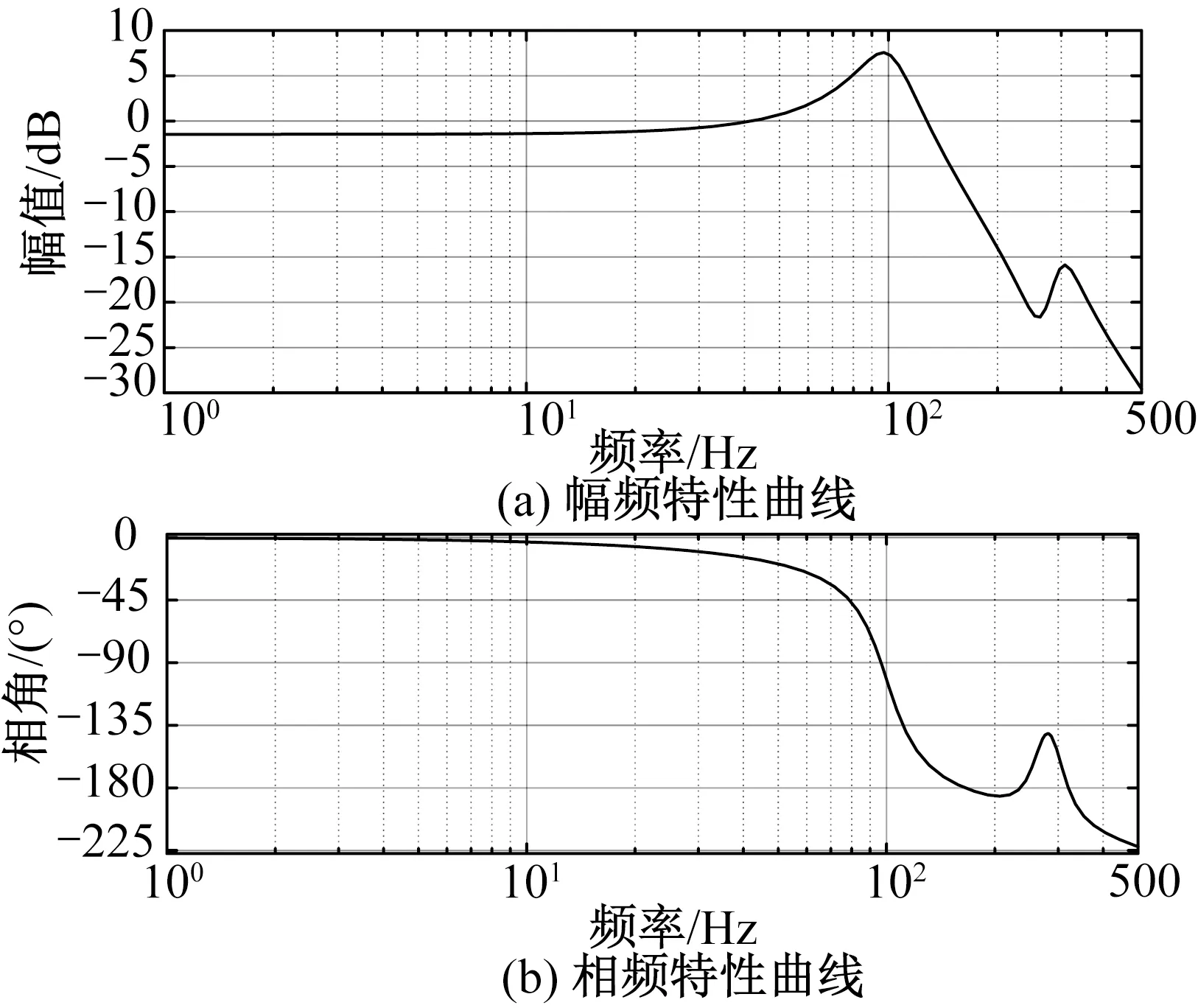
图5 PFSM系统开环传递函数的频率特性Fig.5 Frequency characteristics of open loop transfer function of PFSM system
由幅频特性曲线可知,PFSM系统的传递函数可能为一个惯性环节、一个二阶振荡环节和一个双二阶环节的串联,这也符合之前的模型分析。因系统传递函数包含的参数较多,故在多维空间进行参数搜索很困难。机械谐振往往出现在高频段,由于主函数的衰减作用,因此PFSM系统的幅频特性已在-30 dB水平,转换为绝对值,约为10-2的量级。若将传递函数模型以绝对值表示,则式(11)对幅频特性曲线的影响极小。因此,在辨识过程中,将PFSM系统的传递函数分为式(10)和式(11)两部分,先以式(10)拟合,得到拟合结果后,从测量得到的频率特性中提出式(10),再以式(11)拟合。
由于实测的PFSM系统开环传递函数的频率特性是非线性的,因而使用非线性最小二乘法辨识参数,用幅频模型进行拟合,以相频特性辅助进行结果检验。Matlab的Curve Fit工具箱提供了丰富的曲线拟合功能。将幅频特性以绝对值表示,导入工具箱,同时提供函数模型为式(9)的幅频模型,即
(13)
在Curve Fit里使用非线性最小二乘法进行曲线拟合,同时选择鲁棒性为最小残差法,置信区间为使系数限制有效。非线性最小二乘法需要提供参数初始值,若初始值选择不当,则容易使误差函数陷入局部极小值,不能给出期望的拟合效果。使用Matlab的单输入单输出(SISO)工具,根据传递函数模型选择零极点,构造出一个频率特性与实测的PFSM系统频率特性相接近的传递函数,然后将选择的零极点作为拟合的初始值,从而有效避开局部极小值的影响。式(13)中,将a0,b0,b1,b2的初始值分别设定为1,1×10-7,1×10-3,1×10-4,并限定各参数最小值为0。拟合出的4个参数的值分别为0.856,2.539×10-6,5.388×10-4,3.788×10-4。
拟合出的主传递函数与实测传递函数的频率特性的对比结果如图6所示。根据上述分析,从图6中剔除主传递函数的频率特性,以相同方法拟合机械谐振环节的传递函数。式(11)中,将b3,b4,b5,b6的初始值分别设定为2×10-7,1×10-7,2×10-7,1×10-4,并限定各参数最小值为0,拟合出的4个参数的值分别为3.610×10-7,1.221×10-4,2.825×10-7,1.081×10-4。机械谐振环节幅频特性的拟合情况如图7所示。

图6 主传递函数与实测传递函数的频率特性对比Fig.6 Comparison of frequency characteristics between main transfer function and measured transfer function

图7 机械谐振环节幅频特性拟合情况Fig.7 Fitting of amplitude frequency characteristics of mechanical resonance
综合上述拟合参数,可得出PFSM系统实测频率特性与拟合得到的传递函数频率特性的对比结果,如图8所示。由图可见:经过参数辨识的PFSM系统传递函数幅频和相频特性曲线与实测曲线吻合度很高。实测频率特性与辨识频率特性之间的误差如图9所示。由图可见:在低频段(小于150 Hz),幅频误差小于0.1 dB,相频误差小于1°;在高频段,幅频误差约为0.3 dB,相频误差最大为3°。这一方面是由于系统在高频段对一些小噪声比较敏感,另一方面是由于在辨识中忽略了高频段存在的一些小的机械谐振。不过,拟合误差都在可接受范围内。
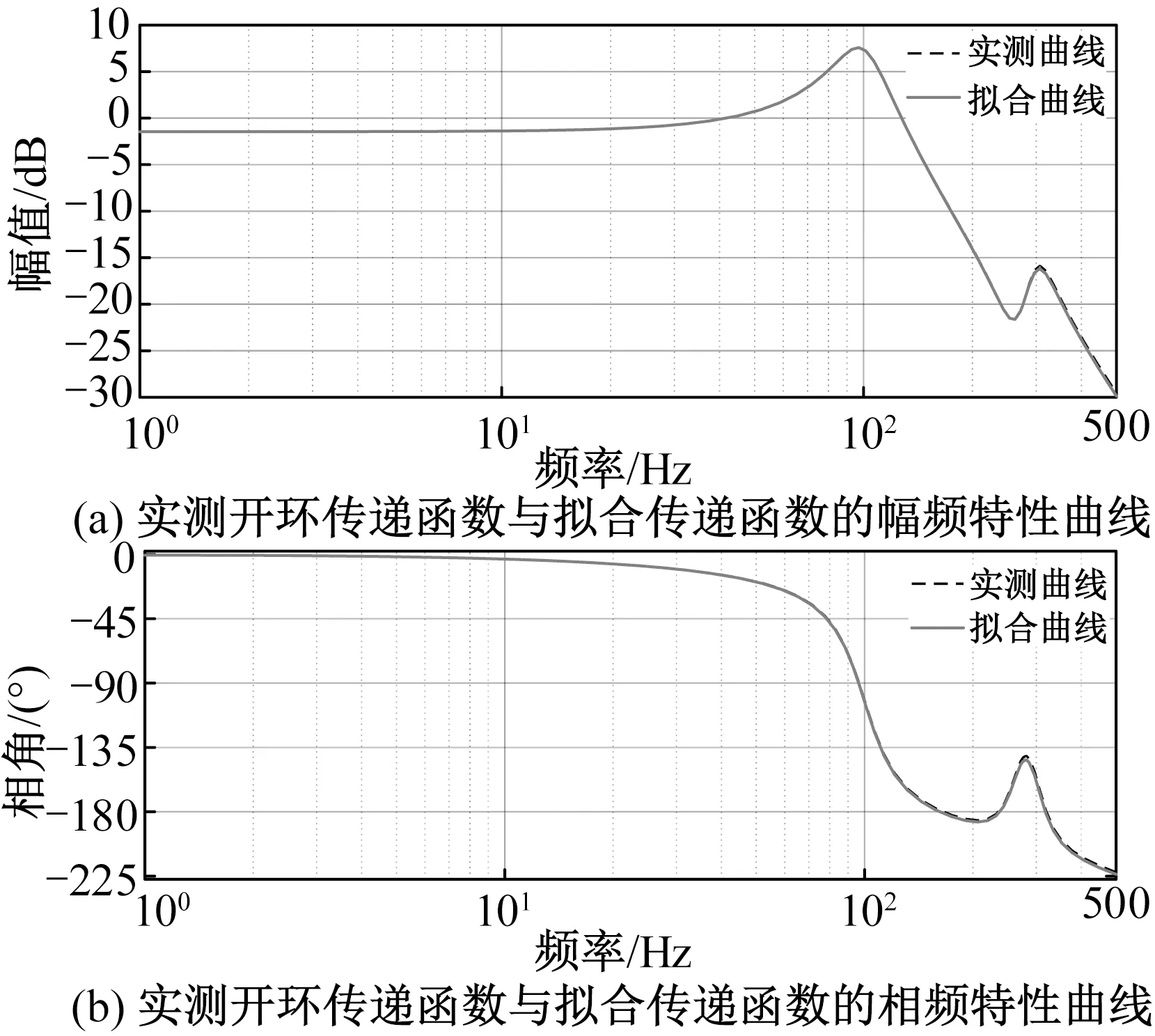
图8 PFSM系统开环传递函数与拟合频率特性Fig.8 PFSM system’s frequency characteristics of open loop transfer function and fitting transfer function

图9 PFSM系统开环传递函数与拟合频率特性之间的误差Fig.9 PFSM system’s frequency characteristic errors between open loop transfer function and fitting transfer function
3 PFSM系统传递函数辨识在实际控制系统中的应用
针对以上分析,为检验辨识效果,设计补偿器为
(14)
则系统开环传递函数变为
(15)
式中:GAD(s)=(1-e-Ts)/(Ts),T为采样时间;KP,TI分别为需要调节的PI控制器参数。采样时间T为0.000 2 s,在仿真时将GAD(s)进行Pade线性化。用式(15)补偿一个惯性环节,其目的是保证补偿器C(s)的分母阶数不小于分子阶数,使之符合因果性。当系统跟踪如下正弦信号时,即
x(t)=12.5sin(10πt)
(16)
调节PI参数,令KP=1.411,TI=1/2 073,此时PFSM系统输出曲线如图10所示,其误差曲线如图11所示。由图可见:对于振幅为12.5 mrad,频率为5 Hz的正弦目标,其跟踪误差最终稳定在0.25 mrad以内。
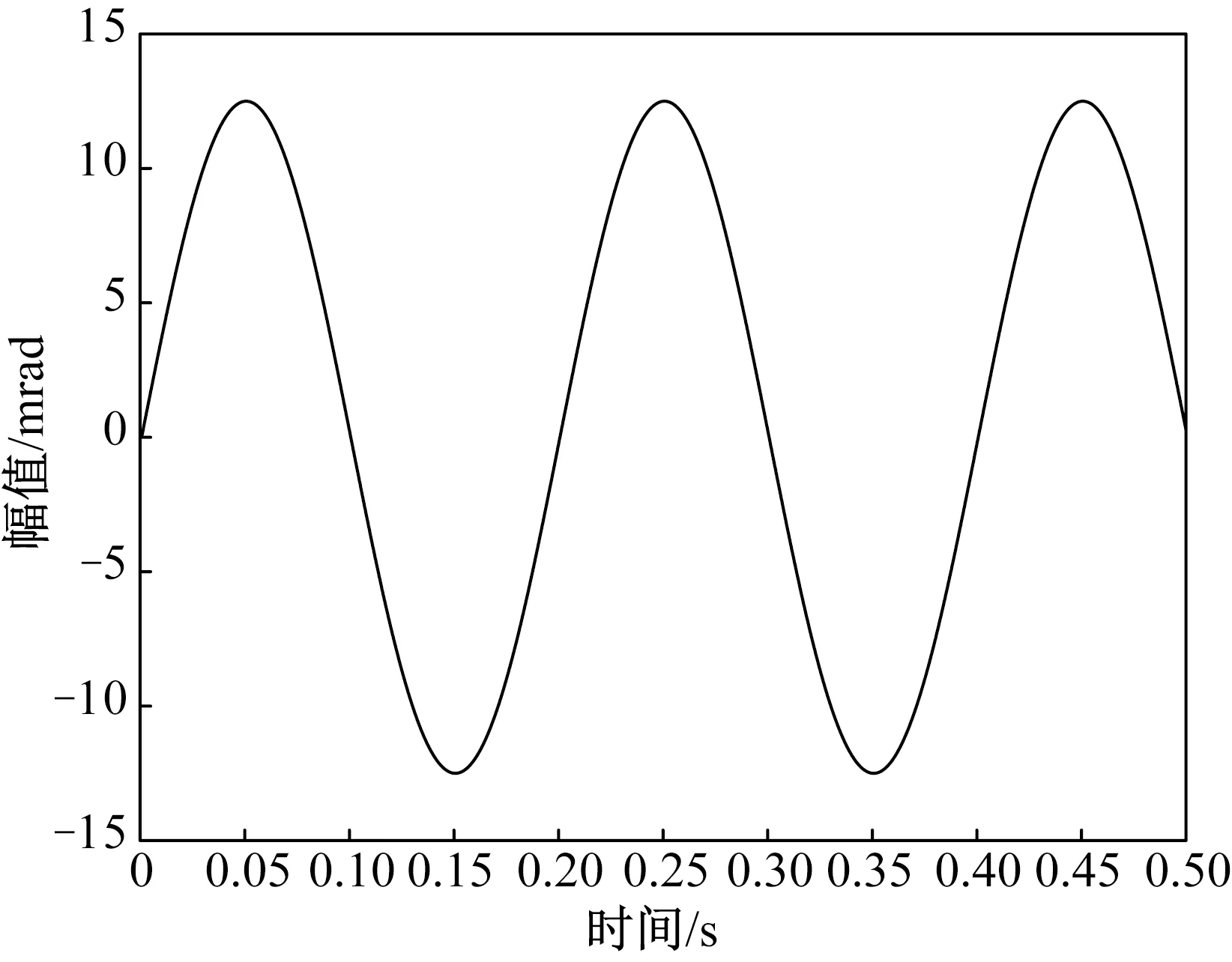
图10 校正后的PFSM系统输出曲线Fig.10 Output curve of corrected PFSM system

图11 校正后的PFSM系统输出误差曲线Fig.11 Output error curve of corrected PFSM system
对于校正后的PFSM系统,其开环频率特性如图12所示。此时,系统的幅值裕度为15.9 dB,相位裕度为61.6°,开环截止频率为308 Hz。如果未对PFSM系统进行校正,则其开环频率特性如图13所示。此时,系统的幅值裕度为4.96 dB,相位裕度为14.4°,开环截止频率为127 Hz,300 Hz处的机械谐振环节会导致该频率附近的误差和噪声放大,降低系统性能。通过双二阶滤波器和经典PI算法,系统的幅值裕度提高了10.94 dB,相位裕度提高了47.2°,开环截止频率提高了181 Hz。
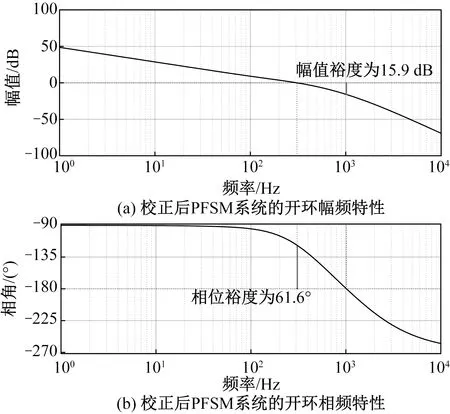
图12 校正后PFSM系统的开环特性Fig.12 Open loop characteristics of corrected PFSM system
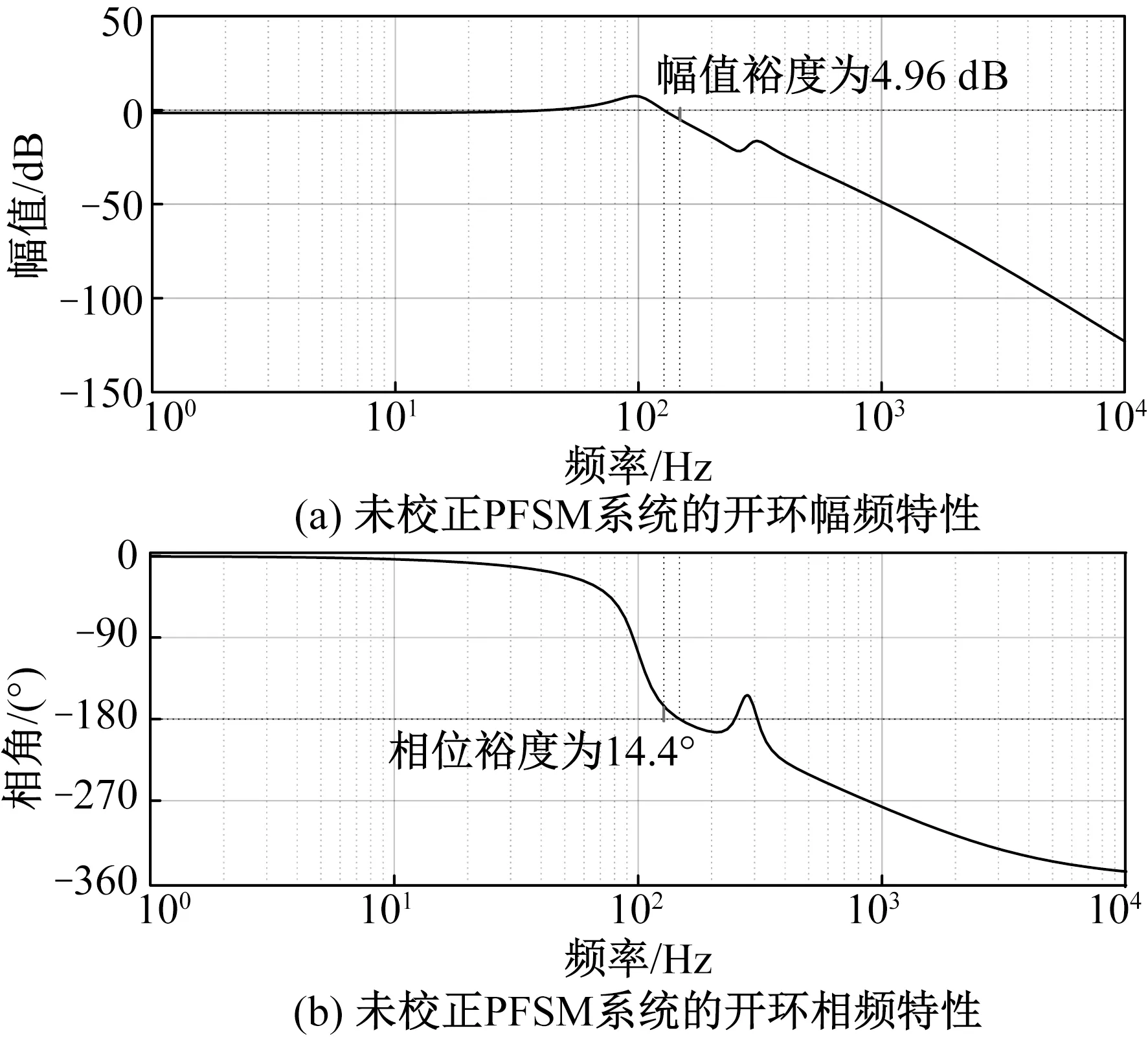
图13 未校正PFSM系统的开环特性Fig.13 Open loop characteristics of uncorrected PFSM system
4 结束语
本文根据压电叠堆材料的特性和反射镜的运动机理,构建了PFSM系统传递函数模型,并结合实测的PFSM系统幅频和相频响应特性,应用非线性最小二乘曲线拟合法,通过Matlab SISO工具箱放置开环零极点,从而选定合适的迭代初值,针对不同频率特性进行分段拟合,得到了精确的PFSM系统传递函数。通过实测传递函数与拟合传递函数的对比,验证了PFSM系统传递函数模型的合理性。由此设计的双二阶滤波器和经典PI相结合的控制算法有效降低了机械谐振的影响,扩宽了控制系统的闭环带宽。通过辨识建立的精确的PFSM系统传递函数,为高性能的光电跟踪系统提供了控制器设计依据。

