QM-40SA机床上下料机器人结构仿真与试验

霍洪鹏， 解福祥， 姜军生， 宋 健

(1. 山东科技大学 机电学院， 山东 青岛 266590; 2. 潍坊学院 机电与车辆工程学院， 山东 潍坊 261061)

0 引 言

目前常用的机床有组合机床、数控机床和加工中心等，根据文献和企业调研，现有的机床大多数是手工上下料，能够实现自动上下料的机床还没有普及[1～3]。手工上下料需要耗费大量的人力、物力和财力。为了解决以上问题，本文针对QM-40SA机床，利用三维建模软件Solidworks以及运动学和动力学仿真软件(Automatic Dynamic Analysis of Mechanical Systems, ADAMS)与ANSYS，设计了一种上下料机器人，针对机器人的零部件进行结构设计和仿真[4-5]。

1 结构分析与设计

结构简化

利用Solidworks根据机器人基本组成：支架、腰座、大臂、小臂、末端及组成平行四边形的拉杆，结合所要求的尺寸和旋转自由度等，初步建立机器人的三维模型。

为了分析机器人各组成构件之间的运动关系，图1(a)为机器人的简化机构。图1(b)中1表示转轴1，其他表示各杆件，设定杆件13与杆件2为连接轴2；杆件3与杆件2为连接轴3，两连接轴安装在同一转座上，其对末端执行器位置为并行驱动，转座又由轴1驱动，整个机构类似于一个串联混合机构。

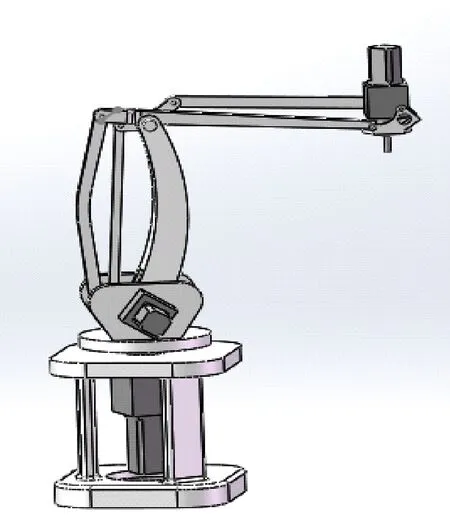
(a) (b)

1-轴; 2～13-杆件

图1 加工中心上下料机器人结构图

由于此结构为两组平行四边形组成，其中主平行四边形确定末端点位置，辅助平行四边形使末端执行器与水平面保持一个固定的姿态。

关节1即为机座转动关节，实现了360°的扭转；杆件2、3、4、5共同组成了平行四边形，且由于杆件3固定在机座上，故其在各关节转动时会一直保持着水平的状态，由于平行四边形结构的特征使得杆件6也一直保持着水平的姿态；杆件6和8为同一构件上，所以杆件6与8之间的夹角不变，杆件8与水平面的夹角也不会改变；同样的杆件11与水平面的夹角不会改变，杆件11与12同属在同一构件，所以末端点12所在面就不会改变，一直保持着水平状态。对于腰部结构如图2所示。

图2中1为大臂，2为连接杆件3(见图1)和杆件2的关节连接轴，3为小臂的连接轴。电动机通过连接减速器再连接在关节轴的两边，左边大臂与轴键连使左边电动机可以带动大臂转动，右边小臂的连接与轴键连，从而右边的电动机可以通过带动小臂连接转动来带动小臂实现俯仰动作。

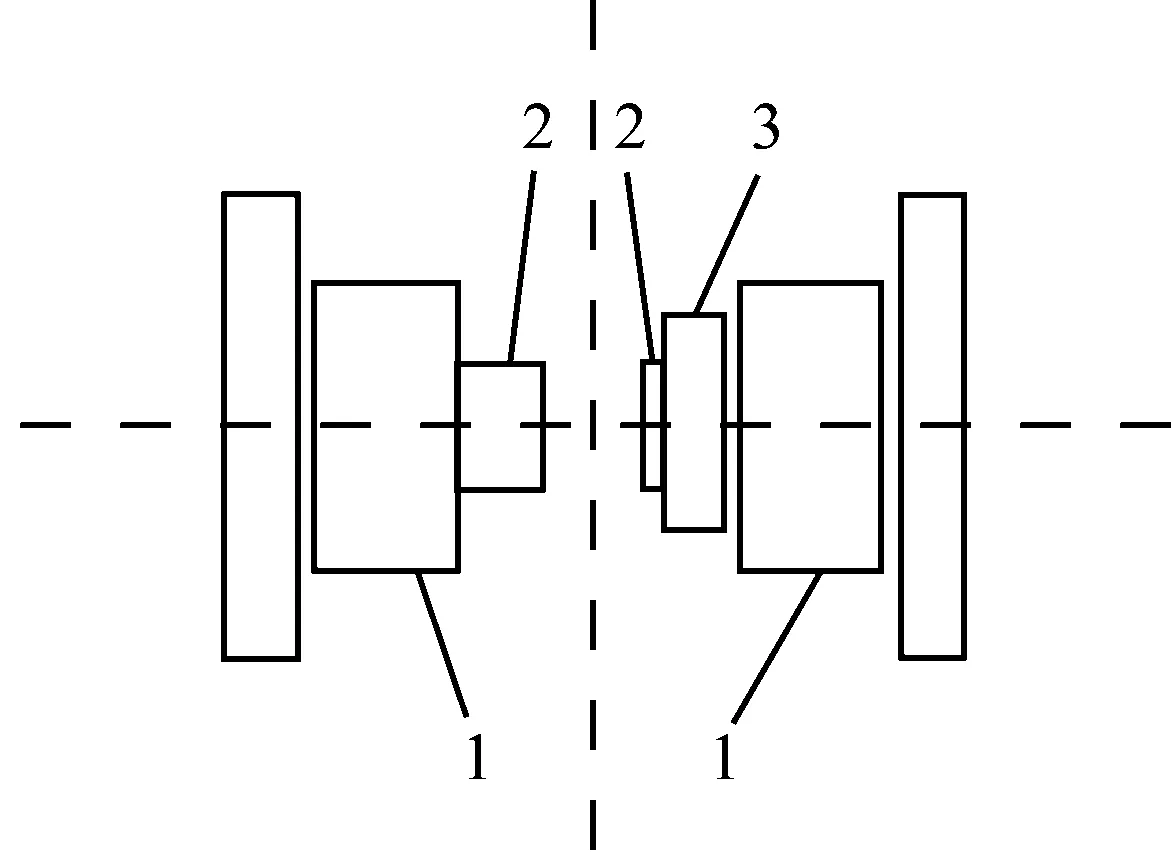
1-大臂; 2-连接轴; 3-小臂连接轴

图2 腰座与大、小臂连接结构

由于结构的特殊性，故影响机器人末端点位置的因素由杆件2的转动，即为小臂的俯仰角度。也是由此两个因素来实现工作空间内的动作。简化结构如图3所示。

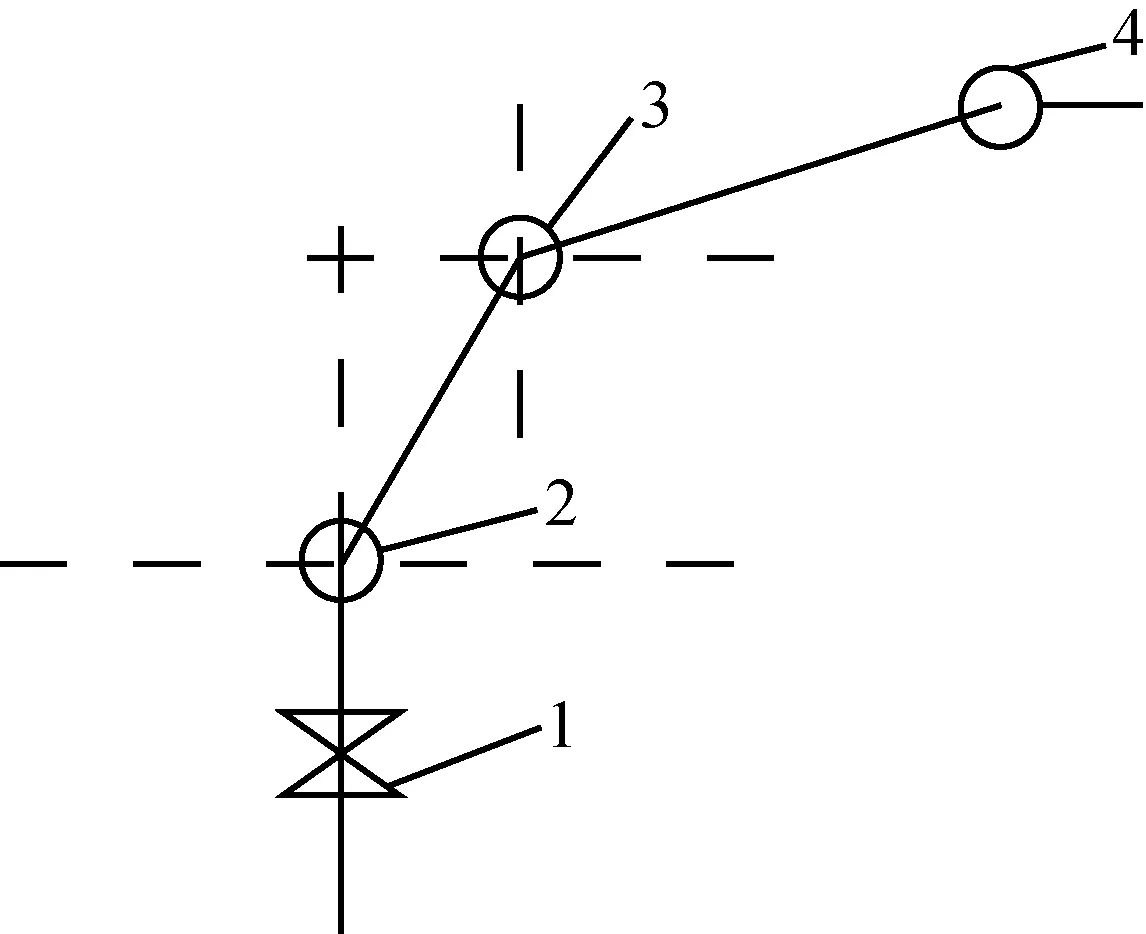
1-腰部; 2-大臂; 3-小臂; 4-末端执行器

图3 机器人结构简化图

2 数据计算

2.1 根据D-H法建立坐标系

为了表示机器人末端执行器的位姿，通常在机器人的末端建立一个相对坐标系。因为空间中的一个点在不同坐标系中位置表示是不同的，所以需要利用不同坐标系之间相互转换关系。定义杆件2与水平面的夹角为β1，以及杆件9与水平面之间的夹角为β2，连杆参数与关节变量见表1。坐标系如图4所示。

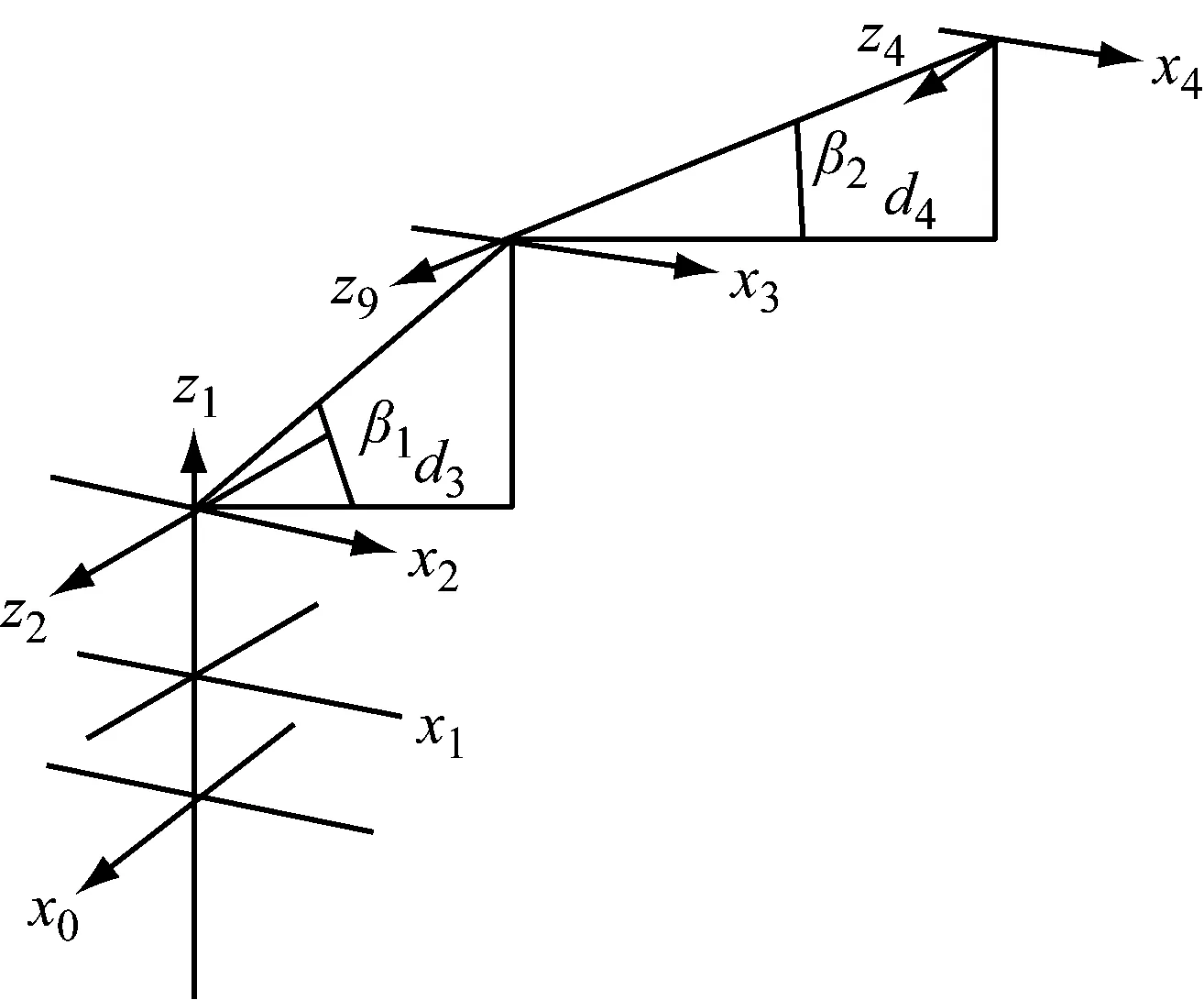
图4 坐标系简化图

图中，在每一个关节处建立坐标系，zi轴在xi-1至xi方向的平移距离di，xi在zi-1至zi方向的平移距离为ai，zi旋转θi角度使得xi-1旋转至与xi平行，xi旋转αi角度使得zi-1旋转至与zi平行。

表1 连杆参数与关节变量

2.2 运动学正解

如果已知关节变量，求解上下料机器人末端执行器相对于参考坐标系位姿的过程为运动学的正解。通过对机构的运动学正解[6-8]分析，可以得出机器人末端的位置，从而知道机器人的工作空间。各个关节的D-H坐标系建立后，通过齐次坐标变换矩阵，求出杆件i-1到i杆的转换。

根据4×4的齐次变换矩阵公式：

Ti=rot(xi,αi-1)trans(xi,a1)trans(zi,di)rot(zi,θi)

依次得杆1转换到参考坐标系转换矩阵：

0T=trans(0,0,a1)rot(z,θ1)=

杆件2转换到杆件1坐标系转换矩阵：

1T=trans(0,0,a2)rot(x,θ2)=

杆件3转换到杆件2坐标系转换矩阵：

杆件4转换到杆件3坐标系变换矩阵：

已知齐次变换矩阵的表达式为：

0T=0T1T2T3T=

由此可知，当杆件2与杆件3一定，安装时βi一定，然后转动后改变的Δβ一定时，那么末端的坐标是一定的。而其中的Δβ大小与电动机转角有关系。

3 仿真分析

3.1 前处理

现利用运动仿真软件ADAMS对机器人进行运动轨迹仿真[9-12]，进一步确定其工作空间与轨迹。将模型Solidworks中另存为x-t格式，以便其在ADAMS中打开。

根据机器人工作时的动作特点和工作对象，在多种驱动方式中选择电动机做驱动方式。电动机驱动效率高、运动速度快、位姿精确度高。现对底座、腰座、大臂、小臂，以及各个拉杆和关节进行运动副的设定，然后在安装电动机的地方设定驱动旋转力。

为了使得仿真成功，需要在仿真前进行各个运动副的检测，在ADAMS/view中的tools工具中选择model verify 选项得到其中model verified successfully表明模型定义成功，现在进行仿真的下一步。

现仅对左右电动机施加转矩，使得假定电动机的旋转带动拉杆驱动大小臂运动，从而完成机器人的工作，由仿真的末端点的轨迹线可以看出,由左右电动机旋转的配合，末端可以完成上下一定角度的弧线运动。其中仿真时对ADAMS中Revolute joint添加motion时，step设置默认值为30.0d*time,此时type选displacement，则参数的实际意义为角速度为30°/s；这样就可以通过电动机与减速器的搭配来适应其工作时速度等[13-15]。

3.2 路径规划

首先，已知机器人的自由度，其主要运动可分为腰座的旋转，大、小的俯仰。分别用电动机控制，为实现对于放置在不同地方的物料，进行位置的准确抓取、放置，对各个部位的轨迹配合记性设计。各个部位的运动顺序的不同可以实现轨迹的不同，如图5所示。

图5 仿真轨迹图

其中在末端抓取物料，经过沿弧线轨迹提升(小臂上仰)，下面如若工作需要可以沿蓝色轨迹将物料放在机器的正前方(大臂的下俯)；倘若需要沿着棕色轨迹放着物料，则为腰座和大臂的下俯共同作用实现。由此可知，电动机的先后运作和合作可以改变末端轨迹路线。通过控制不同电动机的旋转配合，转动速度、方向等因素，可以形成在某一区域的上下料工作动作轨迹。

3.3 速度分析

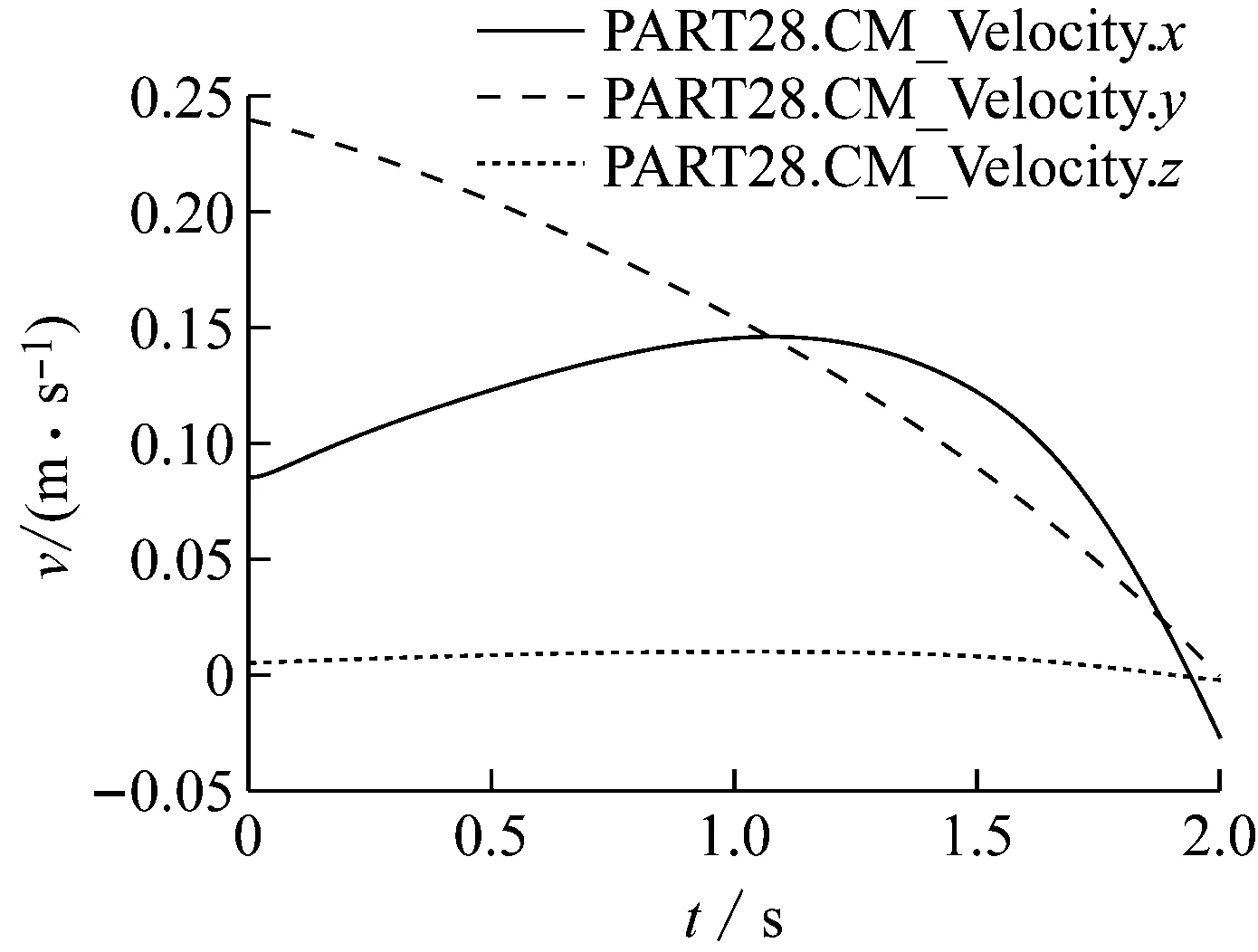
如图6所示，末端执行器连接点从小臂上仰阶段(白色轨迹)，图6(a)可以看出蓝色线y轴速度趋于0，得出机器人在做上仰这一动作到位时的速度恰好为零停止。此时末端所抓取的物料速度也为零，避免了物料上下大幅度的颤动，也避免了对位姿准确精度等关键问题的出现。

(a)

(b)

图6 末端3轴速度和位移曲线

且在图6(b)中可以看出，上仰高度值近0.3 m，z轴坐标线接近水平状态，数值几乎未发生改变，说明末端在做此动作时末端执行器基本保持在x-y面内移动。在z轴上未发生大幅度的偏移，同样保证了末端位置的准确性。

图7为末端旋转与前伸时的位移，可以得出在z轴方向可以旋转或前伸放置1 m外的物料，且y轴位移未变，表明在z-x面内旋转或前伸。y轴并未发生较大数值的偏移，满足平稳的前伸放置物料要求。

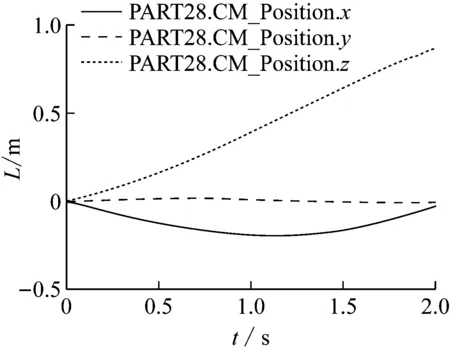
图7 末端3轴位移曲线(前伸或旋转)

通过以上对仿真结果的分析，仿真结果与计算结果相符合，由此也充分可以确定计算运动的动力学方程是正确的。可以进行下一步的承载验证。

3.4 关键部件动力学分析

根据对平常上下料的质量分析，针对数控铣床、磨床等加工物料一般质量在1～10 kg，针对这个质量区间分别进行分析。鉴于机器人总体的结构分析，上下料机器人所有零部件中，小臂处受力面积小，受力大，工作时最易发生形变损坏，因此对小臂进行动力学仿真成为机器人是否能完成工作及设计可行性的依据。

将小臂的三维立体图另存为x-t格式文件，启动ANSYS WORKBENCH后创建static structural 分析，将小臂的x-t文件导入，而后划分网格、施加约束和力并求解[16-17]。首先，设定物料5、10 kg，不同质量的物料总体变形和应力云图如图8所示。

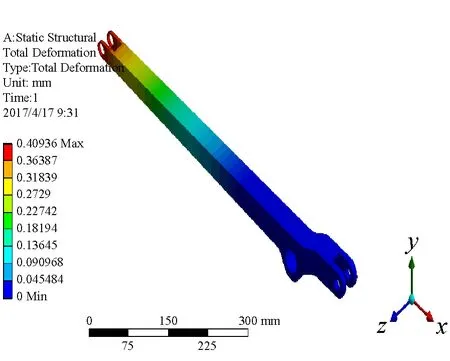
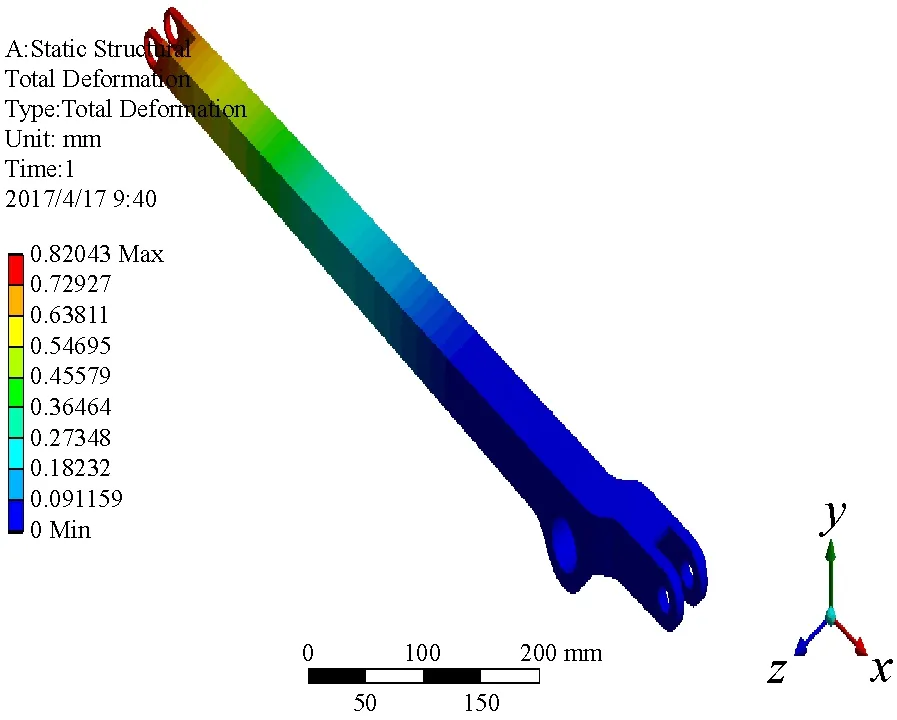
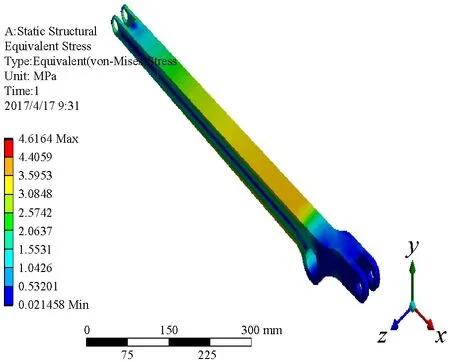
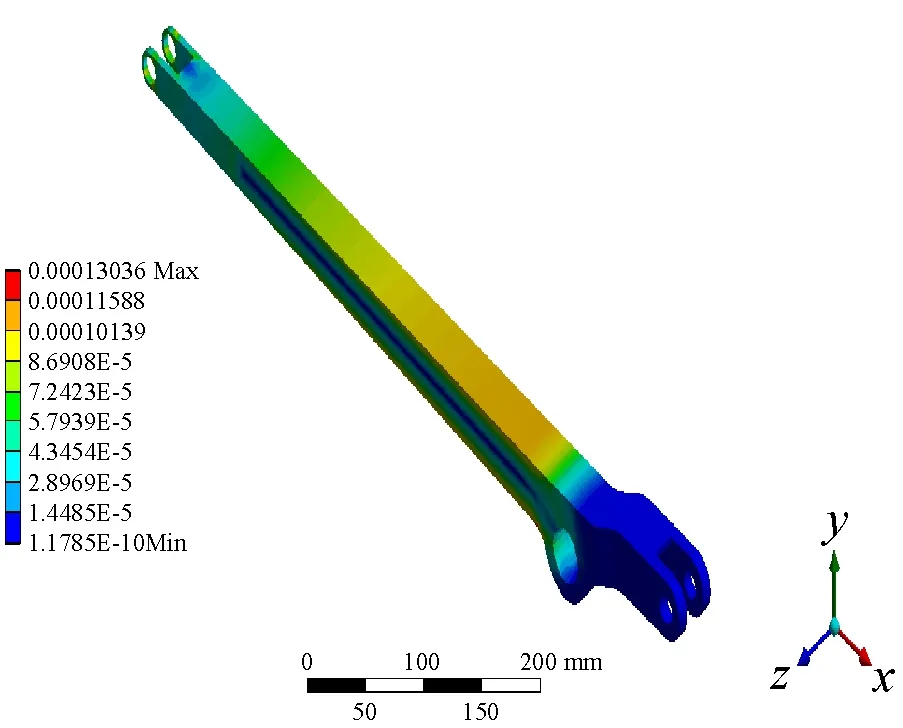
图8 总体变形和应力云图(5 kg、10 kg)

由彩色云图显示的小臂受力时应力应变分布情况，可以形象清楚的看出，小臂在工作时承受的最大应力在与大臂连接和末端连接之间部分，所以在这个区域容易发生疲劳失效，这与实际相符合，而且也能从中得出小臂的受力不影响工作的完成，表明设计的可行性。

3.5 试验验证

机床上下料机器人样机如图9所示。根据末端执行器仿真轨迹线中均匀地选取4个点，现通过试验来验证4个点的实际坐标值，来验证工作的可行性。以起始点作为坐标原点，依次选取坐标点，分别进行5次测量，见表2。

图9 机床上下料机器人样机

根据表2，可以看出试验中末端执行器选定的4个点上x、y、z3坐标偏差都在2 mm内，说明机器可以完成。

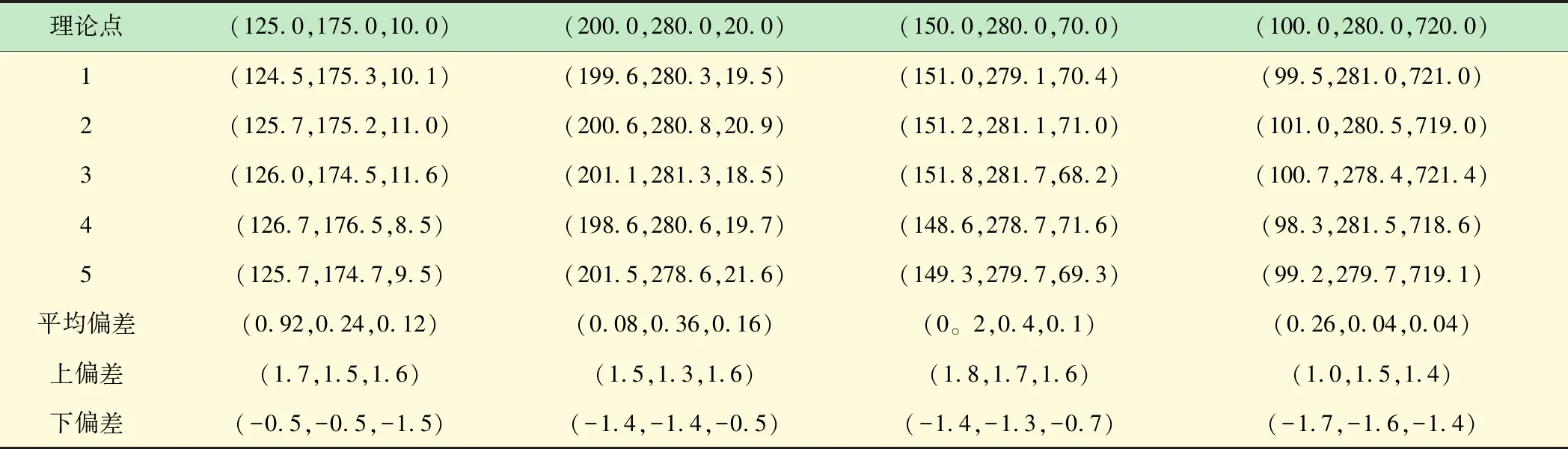
表2 重复定位 mm

4 结 语

(1) 本文对上下料机器人依次做了结构分析，对简化的结构各个关节建立D-H坐标系，然后对机器人末端进行运动学正解，通过Solidworks对其进行三维建模，并进行了样机试制。

(2) 运用运动学仿真软件ADAMS对各个关节添加运动副进行运动仿真，分析其运动轨迹，得到末端的运动速度曲线，作为选择电动机及减速器的依据。

(3) 运用ANSYS仿真软件对上下料机器人的小臂进行动力仿真分析，通过小臂工作时受力最大时的应力云图和总体变形可形象看出，对于1～10 kg的物料，机器人的小臂能够顺利实现上下料。试验结果表明，末端执行器在x、y、z3坐标偏差都在2 mm内。