多参数正则化的动态光散射测量数据反演
申 晋, 修文正, 尹丽菊, 邢雪宁, 刘 伟
(山东理工大学 电气与电子工程学院, 山东 淄博 255049)
0 引 言
动态光散射技术是测量亚微米及纳米颗粒粒度及其分布的有效方法[1-3],该技术是通过测量布朗运动颗粒随时间起伏的散射光强信号来获得动态光散射数据,再对动态光散射数据进行反演得到颗粒的粒度分布[4-6]。动态光散射技术具有非接触、不干扰被测体系原有状态等优点,已经成为亚微米及纳米颗粒测量的一种常用方法。在动态光散射测量时,测量数据反演需要求解的第一类Fredholm积分方程是一个病态方程,即方程解的存在性、唯一性和稳定性均不能得到保证。已经提出的多种动态光散射数据反演方法,包括累积法[7]、NNLS法[8]、CONTIN[9-10]法、指数采样法[11]、奇异值分解法[12]、贝叶斯法[13]以及Tikhonov正则化方法[14]等,这些方法各具特点,但均存在局限,多分散颗粒体系的测量数据反演是动态光散射测量技术在实际应用一直未能得到很好解决的难题。在各种反演方法中,Tikhonov正则化方法以其不受粒度分布形式限制和宽适应性在动态光散射技术得到广泛应用。随着动态光散射技术应用领域的不断拓宽,其在多分散颗粒体系测量应用中存在的不足愈加明显:正则参数取值过大会导致有用信息丢失,无法分辨较近的峰值;而过小则会引起解的振荡。为得到稳定的反演结果,通常会选择牺牲部分有用信息,这导致了多峰分布颗粒的求解困难。在进行微米级颗粒测量的前向激光散射技术中,林承军等[15]通过构建一个由多个参数控制的带通滤波函数,在对正则解进行非负约束的条件下,分别控制正则解的振荡程度和解的高度,降低了正则解的振荡和负值并能较好地识别多峰。
本文在动态光散射测量中,采用多参数正则化方法,通过调节因子构造多个不同正则参数共同作用于正则矩阵,利用抑制小奇异值对反演结果的影响,提高反演方法的抗噪性能和多峰识别能力,有效地消除了反演的颗粒粒度分布中的虚假峰,得到了准确的多分散的亚微米颗粒体系的反演结果。
1 动态光散射与多参数正则化
在动态光散射测量技术中,光强自相关函数:
(1)
式中:B为测量基线;β为相干因子;g(1)(τ)为归一化电场自相关函数。
对于单分散颗粒体系:
g(1)(τ)=exp(-Γτ)
(2)
多分散体系:
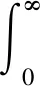
(3)
其离散化形式为:
(4)
i=1,2,…,N;j=1,2,…,M
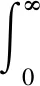
q为散射失量;m是溶液的折射率;λ0为激光的波长;θ是散射角;DT为颗粒的平移扩散系数,
(7)
kB、T、η和D分别是Boltzman常数、绝对温度、分散介质的黏性系数和颗粒的流体动力学直径。通过求解式(1)~(7),可得到待测颗粒的粒度分布。
对于多角度动态光散射测量,归一化的电场自相关函数的离散形式的表达式为:
式中:散射角θr=θ1,θ2,…,θR,kθr是对应散射角θr的自相关函数的权重系数;CIθr,Di为Mie散射系数,即粒度为Di的颗粒在散射角度θr处的散射光强分数,可通过Mie理论计算获得;fDi为所求的颗粒粒度分布。将式(9)代入式(8)得:
(11)
其向量形式为:
(12)

式(4)可写成算子方程形式:
Ax=b
(13)
矩阵A∈RM×N(M≥N)为Hilbert空间X到B的有界线性算子,x∈X,b∈B,其元素为exp(-Γiτj),x的元素为G(Γi),b的元素为g(1)(τj)。Tikhonov正则化方法通过优化目标函数
(14)
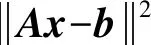
(15)
s>0,b≥1,x∈X
在Tikhonov正则化方法中,所有奇异值对应相同的正则参数,正则参数受噪声影响往往会导致所求的解出现欠正则化,使反演的颗粒粒度分布中出现虚假峰、毛刺、峰值分瓣等情况,导致双峰及多峰的分辨率显著降低。反演过程中,任何极微小的计算误差与实验误差都会被小奇异值放大,引起反演结果的剧烈变化。
为了解决上述问题,可通过调节因子构造正则参数函数,使多个不同的正则参数共同作用在正则矩阵(微分算子模型)上。多参数正则化的目标函数为:
(16)
其矩阵形式为:
(ATA+α2L)x=ATb
(17)
α=[α1,α2,…,αj](j=1,2,…,M)。对式(13)中的矩阵A进行奇异值分解:
(18)
得到解:
(19)
式中:U∈Rm×m与V∈Rm×m为酉矩阵;S∈Rm×m为对角矩阵;σj为奇异值,由于小的奇异值会对误差进行放大,因此,需对其进行截断;μj与vj分别为正交矩阵U和S的列元素,通过调节因子η调节正则参数:
αj+1=(η×αj)1/r
(20)
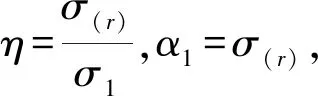
2 粒度反演的数值模拟
反演的双峰(466/915 nm、316/470 nm)和三峰(324/601/871 nm)颗粒粒度分布均采用Johnson’s SB分布函数[19]:
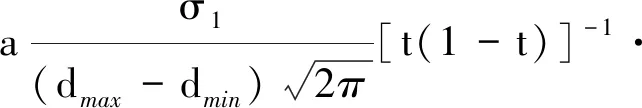
(21)
式中:dmin和dmax分别为最小和最大颗粒粒径;参数t是归一化颗粒粒径,t=(d-dmin)/(dmax-dmin),μ1,σ1,μ2,σ2,μ3,σ3,a,b,c为颗粒粒度分布的参数。为更接近实际测量情况,对模拟的光强自相关函数数据依次加入噪声水平δ为10-4和10-2的随机噪声。含噪的光强自相关函数
(22)
式中:ε为随机噪声。为检验反演性能,引入反演性能指标:

表1 粒度分布模拟参数
(a) 噪声水平为0
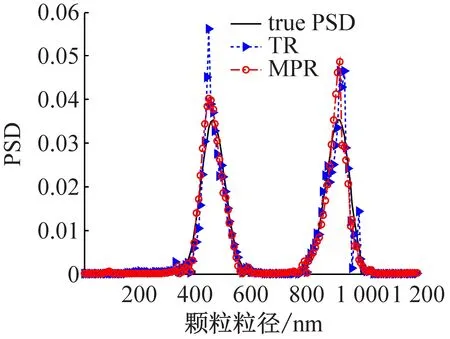
图1 466/915nm双峰颗粒体系MDLS数据在不同噪声水平下不同方法的反演结果
(a) 噪声水平为0
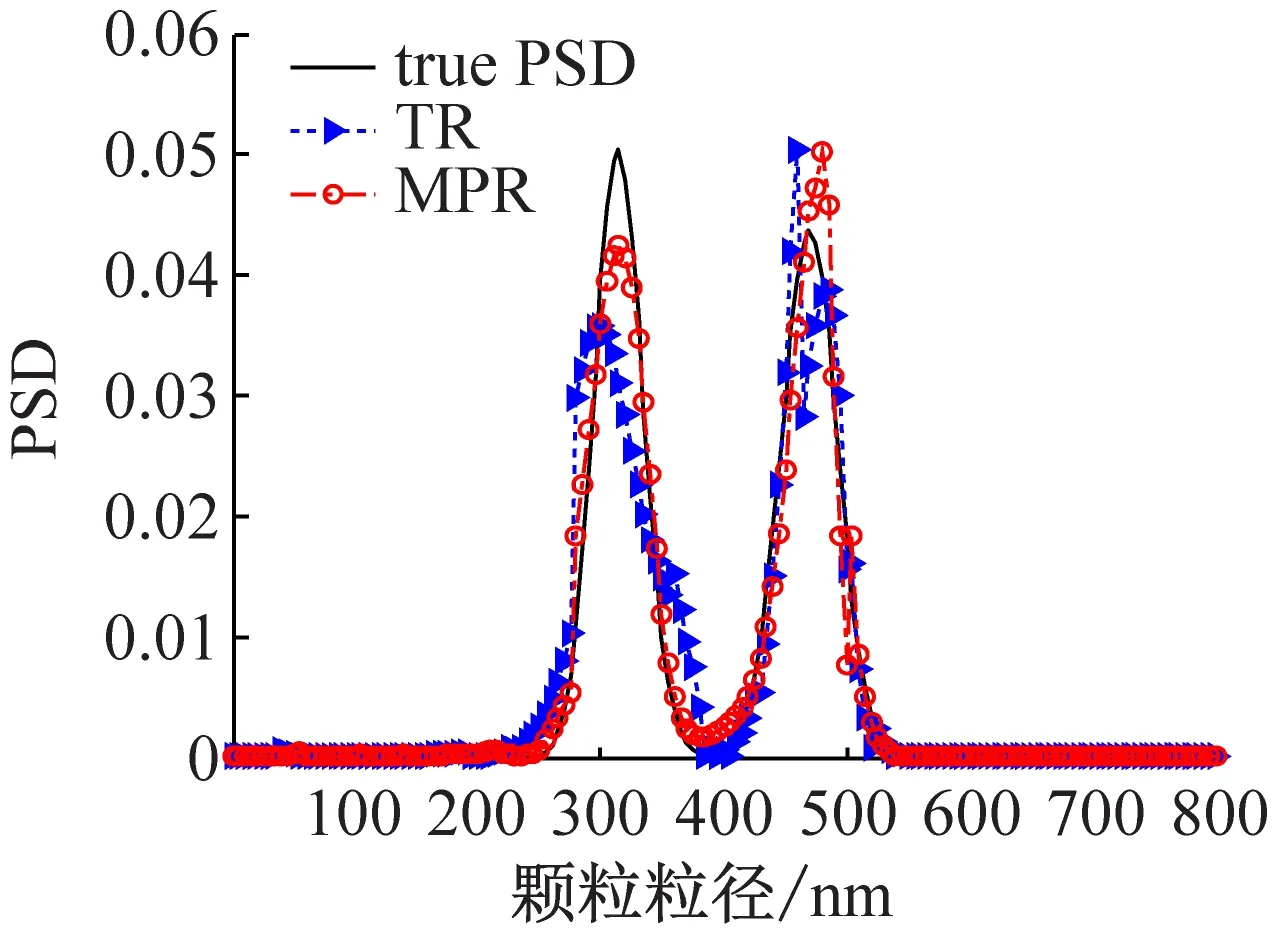
图2 316/470 nm双峰颗粒体系MDLS数据在不同噪声水平下不同方法的反演结果
(a) 噪声水平为0

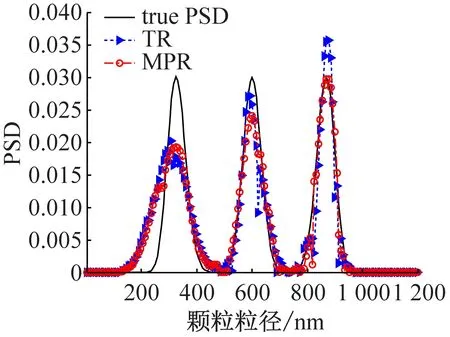
图3 324/601/871 nm三峰颗粒体系MDLS数据在不同噪声水平下不同方法的反演结果

表3 316/470 nm双峰颗粒体系MDLS数据在不同噪声水平下的反演性能指标

表4 324/601/871 nm三峰颗粒体系MDLS数据在不同噪声水平下的反演性能指标
从图1与表2可以看出,对于466/915 nm的双峰颗粒体系,多参数正则化方法获得的颗粒峰值误差与分布误差均小于Tikhonov正则化方法的误差,在噪声水平为0时,Tikhonov正则化方法反演的双峰颗粒粒度分布相对误差为0.044 6,峰值误差为0.032 2/0.008 7/0.025 1,而通过多参数正则化方法可使相对误差降为0.030 7,峰值误差为0.032 2/0.008 7;当噪声水平为10-2时,Tikhonov正则化方法反演的双峰颗粒粒度分布相对误差为0.080 2,峰值误差为0.032 2/0.008 7,而通过多参数正则化方法可使相对误差降为0.047 4。由于受噪声影响,通过Tikhonov正则化方法反演的颗粒粒度分布中常有毛刺出现,当毛刺出现在峰值附近时,会出现峰值分瓣现象,导致对测量结果的误判。不难看出,多参数正则化方法反演明显改善了上述情况,反演结果更逼近真实颗粒粒度分布。
从图2与表3可以看出,与真实颗粒粒度分布相比,Tikhonov正则化方法反演所得的颗粒粒度分布除产生毛刺外,316 nm明显展宽。在噪声水平为0时,Tikhonov正则化方法的分布误差为0.060 8,多参数正则化方法的分布误差为0.030 9;当噪声水平增加到10-2时,前者的分布误差为0.078,后者为0.052。随着噪声水平的增加,Tikhonov正则化反演的第一个峰的毛刺增多,而多参数正则化明显改善了这一情况。
从图3和表4可以看出,对于324/601/871 nm三峰颗粒体系,采用Tikhonov正则化方法反演得到的324 nm处峰值附近出现明显毛刺,毛刺数量随噪声水平越大而越多。在噪声水平达10-2时,多参数正则化方法仍能得到稳定的三峰粒度分布结果。
3 实验结果与讨论
实验所用数据为(306±8)nm和(974±10)nm标准聚苯乙烯乳胶颗粒的动态光散射实测数据,来自本课题组合作方——阿根廷Institute of Technological Development for the Chemical Industry 的Jorge R. Vega教授课题组。相关的实验参数为:激光波长632.8 nm,分散介质折射率nm=1.33,测量温度T=298.15 K。散射测量角θ=30°,50°,70°,90°,110°,130°。从图4和表5可以看出,Tikhonov正则化方法反演的颗粒粒度分布在974 nm峰处出现两个虚假峰,多参数正则化方法反演结果中则没有这种现象,且在306 nm处的峰值误差远小于Tikhonov正则化方法(超过1个数量级)。
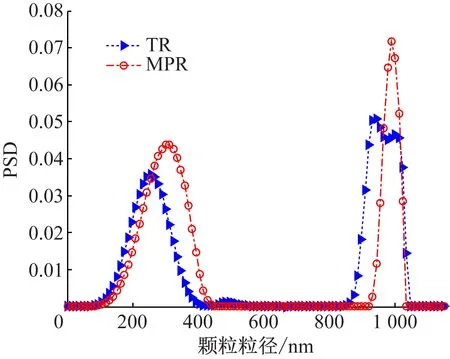
图4 306/974 nm双峰颗粒体系的反演结果

Size/nmTRMPR峰值/nmV2峰值/nmV2306/974255/943/1 0010.166 7/0.031 8/0.027 7300/9890.019 6/0.015 4
无论是数值模拟还是实际测量,采用多参数正则化方法可得到比Tikhonov正则化方法更为准确的反演结果。在Tikhonov正则化方法中,所有奇异值均采用同一个正则参数处理,正则参数过大或过小会导致反演的颗粒粒度分布过于平滑或产生毛刺与虚假峰,在多参数正则化方法中,通过采用不同量值的正则参数分别处理不同的奇异值,避免了因正则参数过大或过小引起过正则化或欠正则化现象。由于任何微小的实验误差或计算误差都会被小的奇异值放大,通过截断奇异值分解将小奇异值截断,有效地抑制了小奇异值的放大作用,进而提高了反演方法的多峰的识别能力与抗噪能力。从反演机理上可以看出,与Tikhonov正则化方法相比,多参数正则化方法在多峰颗粒体系测量中具有明显优势。
4 结 语
为了提高动态光散射技术在测量双峰及多峰颗粒体系的准确性,在正则化反演中,通过截断奇异值分解截去小的奇异值,再通过调节因子构造正则参数函数,实现了多参数正则化的动态光散射测量数据的反演。对小奇异值的截断处理以及通过多个参数共同调节正则参数,既抑制小奇异值对反演结果的影响,又避免了正参数选取不当导致的过正则化或欠正则化,显著提高了反演方法的抗噪能力与多峰识别能力,在测量时有效地消除了颗粒粒度分布反演中的虚假峰与毛刺的同时,保留更多的颗粒粒度信息,从而增强了多峰分布的识别能力,实现了多峰颗粒体系的准确测量。

