三自由度柔索并联搬运机器人的运动学和工作空间分析

张 龙, 王世伟, 牛 奔, 戴振振

(淮南师范学院 机械与电气工程学院， 安徽 淮南 232038)

0 引 言

搬运机器人目前广泛应用于加工生产线、包装码垛等行业，用以实现自动化搬运作业。传统的搬运机器人大多采用串联机械臂[1]，存在承载能力低、定位精度差等问题，难以适用于重载、高定位精度的场合。

柔索并联机构作为一种采用柔性绳索代替刚性连杆作为驱动元件的并联机构，具有负载能力强、运动速度快、可重构等优点[2]。近年来，随着科学技术的不断发展，各国研究人员利用柔索并联机构的结构特点，将其广泛用于天文观测、建筑施工、救援、医疗康复服务等方面[3-5]。

文中基于柔索并联机构设计了一种三自由度搬运机器人，首先对其结构进行了描述，接着建立了机器人的运动学模型，给出了运动学正逆解。在此基础上，依据静力学方程和矢量封闭原理，分析了该机器人的可控工作空间。最后在给定结构参数下，运用Matlab软件对其运动学和可控工作空间进行了仿真实验。

1 系统描述

三自由度柔索并联搬运机器人结构如图1所示。

1.滚筒; 2.直流伺服电机; 3.张紧滑轮; 4.柔索; 5.导向滑轮; 6.支撑横梁; 7.搬运重物; 8.支撑架; 9.底盘; 10.联轴器。

直流伺服电机共有4个，其中3个均匀布置在正三角形底盘顶端，1个布置在底盘中心的正下方；支撑架安装在底盘顶点，其下部设置有张紧滑轮，顶端设置有导向滑轮；直流伺服电机与卷筒连接，卷筒上绕有柔索；前3条柔索经张紧滑轮、导向滑轮分别与重物连接；第4条柔索穿过底盘上开设的导向孔后与重物连接。

直流伺服电机通过牵引4根柔索完成重物的空间三维平动。

2 运动学分析

2.1 坐标系建立

由于文中研究的柔索搬运机器人中的柔索长度较短，可以忽略柔索的自重、变形和垂度，因此用直线代替柔索。另外,在对机构进行受力分析时，忽略杆件变形和各连接处的摩擦。基于以上分析，得到三自由度柔索并联搬运机器人的机构简图如图2所示。

图2 三自由度柔索并联搬运机器人机构简图

由图2可以看出，Ai表示底盘顶点，Bi表示支撑架顶点，Ci表示正三角形重物顶点。定义坐标系{O}为全局坐标系，原点位于底盘的重心上，x、y轴固定在Ai所在底盘平面上，z轴垂直于Ai所在底盘平面，方向向上；定义坐标系{O′}为局部坐标系，原点位于搬运重物的重心上，x′、y′轴固定在Ci所在平面上，z′轴垂直于Ci所在平面，方向向上。底盘的边长为a，重物的边长为c，支撑架的高度为h。

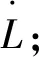
2.2 运动学逆解分析

因为重物在空间中做三维平动，所以其姿态变换矩阵[6]为

由图2得前3条柔索长度矢量

(1)

式中:Bi----坐标系{O}原点到支撑架顶点的矢量,i=1，2，3;

r----坐标系{O}原点到坐标系{O′}原点的平移矢量;

Ci----坐标系{O′}原点到柔索与重物铰接点的矢量。

第4条柔索长度矢量

L4=OO′=r(2)

各条柔索的单位方向矢量为：

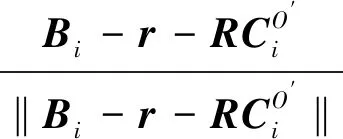
各条柔索的长度为:

Li=‖Li‖ (4)

i= 1，2，3，4

2.3 运动学正解分析

已知4根柔索的长度Li，求解重物重心的位置(xO′,yO′,zO′)，即为该机器人的运动学正解。

根据2.1所述的已知条件得：

r=[xO′,yO′,zO′]T

将上述矢量代入式(1)～式(4)得各条柔索长度对应的方程为：

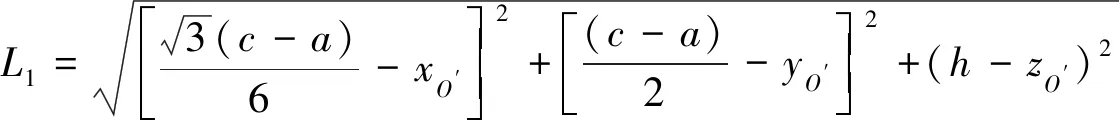
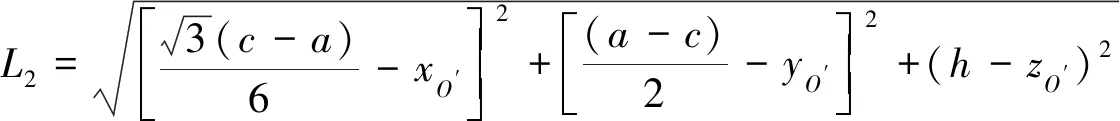
L3=3(c-a)3-xO′éëêêùûúú2+y2O′+(h-zO′)2(7)L4=x2O′+y2O′+z2O′(8) 联立方程组(5)～(8),即可求得重物重心的位置(xO′,yO′,zO′)。3 可控工作空间分析 重物在运动过程中如果满足受力平衡和力矩平衡,且每条柔索拉力均大于零的所有位姿的集合定义为其可控工作空间[7-8]。对该搬运机器人进行受力分析,根据重物的受力平衡关系得静力学方程∑4i=1Fi+FP=0∑4i=1ki×Fi+MP=0ìîíïïïï(9)式中:Fi柔索拉力,Fi=fiui,N;FP重物所受的外部作用力,N;ki柔索拉力作用于重物的力臂O′Ci,m;MP重物所受的外部作用力矩,N·m。将式(7)写出矩阵形式有:JT×F=W(10)式中:JT柔索并联搬运机器人的Jacobi-an矩阵的转置矩阵,且JT满足:JT=u1u2u3u4k1×u1k2×u2k3×u3k4×u4éëêêùûúúF=f1f2f3f4[]TW=-FPMP[]T求解式(8),可以得到柔索拉力为F=(JT)+W+[I-(JT)+JT]λ(11)式中:(JT)+矩阵H的Moore-Penrose广义逆矩阵;λ任意一个列向量。根据矢量封闭原理[7],如果由重物位姿计算出的I-(JT)+JT中的每个元素均大于零,则牵引重物的柔索拉力大于零,也即该位姿落在可控工作空间内。4 仿真实验4.1 可控工作空间仿真实验给定柔索并联搬运机器人的结构参数见表1。表1 结构参数参数数值底盘边长a/m2.0重物边长c/m0.2支撑架高度h/m1.5 采用Monte-Carlo方法,在MATLAB中编程仿真[9],求出该机器人的可控工作空间如图3～图6所示。