采用自适应死区补偿耦合自适应级联控制的液压执行机构优化

王 华,杨可可,刘析辉

(1.新乡职业技术学院 数控技术系,河南 新乡 453000; 2.吉林大学 机械科学与工程学院,长春 130025)

众所周知,现代工业的自动化越来越普及,自动化工程中机械定位系统的精确性至关重要.电动、液压以及气动等方式是通过执行机构驱动的定位系统,而液压执行机构在实际应用中广受欢迎[1].但是,液压执行机构具有非线性、参数不确定性和轻微的动态衰减等缺陷,从而降低了它的精度,限制了它在闭环控制器中的应用[2].因此,研究液压执行机构高精度的控制方法,对于促进液压技术的发展具有重要意义.

为了提高液压执行机构在实际应用中的控制精度,许多学者对液压执行机构的控制方法进行了研究.例如:文献[3-4]研究了液压执行机构的开关电磁阀控制,建立定位系统的控制模型,通过仿真验证控制系统的定位误差,从而改善了液压执行机构的定位冲击;文献[5-6]研究了自动变速器液压执行机构控制方法,建立变速器液压执行机构的动力学模型,设计离合器回油管路液压执行机构,通过仿真验证滑阀位移曲线,提高了执行机构的定位精度;文献[7-8]研究了水下液压执行机构控制方法,设计了液压执行机构控制流程,对液压执行机构主要参数进行求解,通过仿真检验液压执行机构定位误差,提高了液压执行机构运动轨迹精度.但是,以往研究液压执行机构,控制策略没有考虑死区现象,导致实际追踪误差较大.对此,本文创建液压执行机构平面简图,采用自适应死区补偿耦合自适应级联控制方法,针对执行机构运动轨迹误差最小化问题,采用差分进化算法优化控制器参数.通过Matlab软件对执行机构运动轨迹误差进行仿真验证,为深入研究液压执行机构的控制方法提供理论依据.

1 液压执行机构数学模型

本文所考虑的液压执行机构如图1所示.

图1 液压执行机构Fig.1 Hydraulic actuator

图1中,M为系统总质量,B为黏性摩擦系数,ps为供给压力,p0为返回压力,p1和p2分别为气缸1和2的压力,v1和v2是气缸1和2中的体积,A为气缸活塞的横截面积,Q1为阀门到腔室1的流量,Q2为腔室2到阀门的流量,u为施加在电磁阀上的电压.

重叠比例阀的阀芯凸台大于阀体的环形部分,导致在阀芯位移和流量之间的关系中出现死区.带有死区的阀门在制造过程中所需要的精度低,而且更廉价.

液压执行机构的数学模型[9]为

(5)

式中:f=βv[(0.5v)2-(Ay)2];xv为阀芯位置;p为气缸室压力差;β为体积模量;v=v1+v2;Kh为液压常数;g=(ps-sgn(xv)p)1/2;Kem为阀常数;ωv为阀门带宽;xvb为死区之前的阀芯位置;br为右断点;bl为左断点.

图2以一个框图的形式展现了输入电压u与阀芯位置xv的关系.xvb是由阀门一个内部传感器所测得,并能在电磁阀上获得的信号.

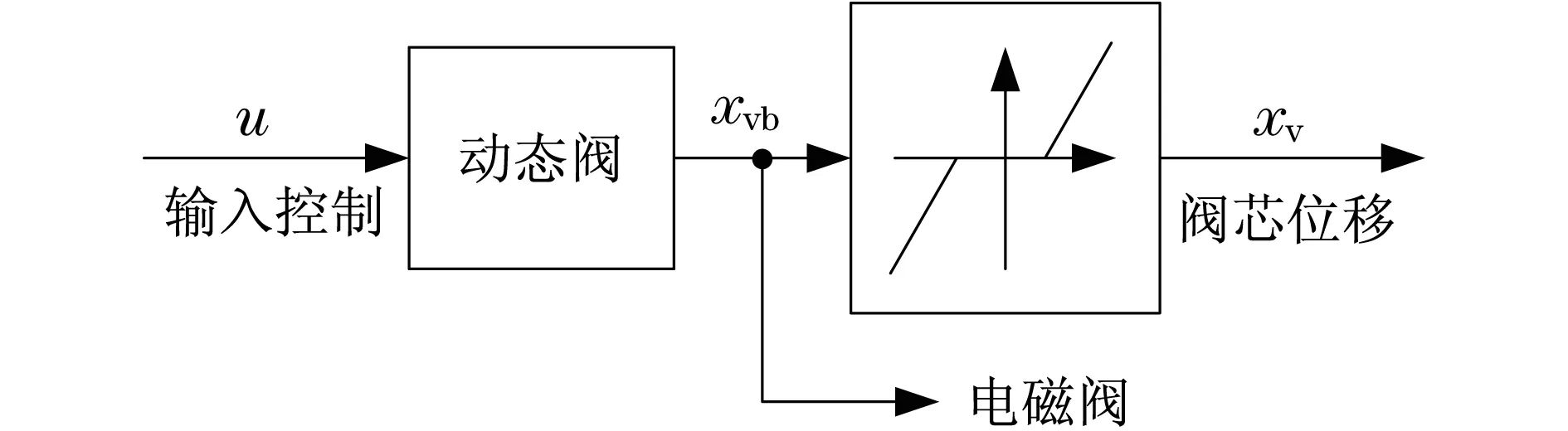
图2 带有死区阀门的框图Fig.2 Block diagram with dead-zone valve

2 控制器设计

适用于液压执行机构的级联控制将液压执行机构数学模型分为两个互联的子系统,一个液压子系统和一个机械子系统,如图3所示.它可以概括为:① 为机械子系统计算一个控制律pd(所需的压力差),以便输出y能够尽可能地追踪轨迹yd;② 为液压子系统计算一个控制率u,以便p能够尽可能追踪轨迹pd.

机械子系统自适应控制法则[10]为

(6)

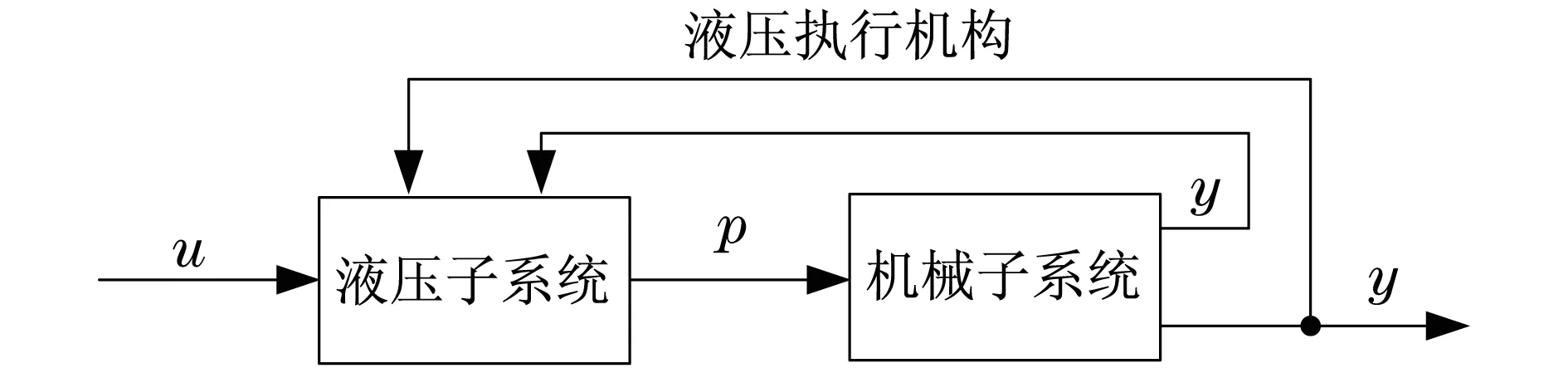
图3 互联的子系统Fig.3 Interconnected subsystems

机械子系统适应法则[10]为

(7)

式中:Γ为正对称矩阵.

液压子系统控制法则为

(8)

(9)

式中:xvd为阀芯位置运动轨迹;xv1为阀芯运动轨迹追踪偏差;p1为压力差;α为液压常数的倒数;τv为阀门时间常数;α1和τv1为估计参数;φ1和φ2为正常数;Kp为负常数.

液压子系统适应法则[10]为

式中:φ3和φ4为正常数.

在自适应死区补偿发展中,假设xv和xvd存在xvb=Kemu这样的关系,得

xv=DZ1(Kemu)=DZ2(u)

(12)

(13)

式中:pr=br/Kem;pl=bl/Kem.

带有自适应死区补偿的自适应级联控制器算法[10]如下所示:

式中:η1,η2和prmax为正常数;plmin为负常数.

预估的左(右)阀门死区断点参数必须总是负(正)的,因此,对式(15)和(16)修改为

(17)

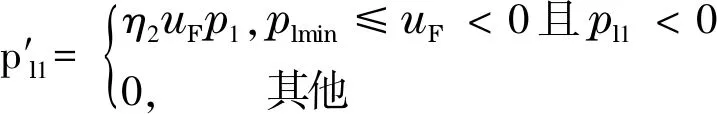
(18)

3 控制器优化设计

差分进化(Differential Evolution,DE)算法从一个随机初始化种群开始,经过变异、交叉和选择操作产生下一种群,该过程经过多次迭代,直到满足条件为止[11].优化的具体步骤如下:

步骤1初始化参数设置.用户必须选择控制DE算法的关键参数,即种群大小(N)、优化变量的边界约束、突变因子(fm)、交叉率(rc)和停止标准(tmax).

步骤2初始化个体.初始化计数器t=0,同时根据n维问题空间中的均匀概率分布生成的随机值,初始化每个决策变量的上限和下限的个体种群(解向量)x(t).在本文中,解向量由Kp,Kd,Kv的潜在解决方案给出.

步骤3评估目标函数值.对于每个个体,评估其目标函数值,采用的最小化目标函数是积分时间平方误差(Integral Time Square Error,ITSE).

步骤4突变操作(或差分操作).根据下面的等式[12]变化个体,即

zi(t+1)=xi1(t)+fm[xi2(t)-xi3(t)]

(19)

式中:xi(t)为第i个种群位置;zi(t)为突变向量的第i个个体位置;fm为突变因子.

步骤5交叉操作.对于每个突变向量,采用均匀分布随机选择一个指数和一个试验向量,通过下式[12]生成,即

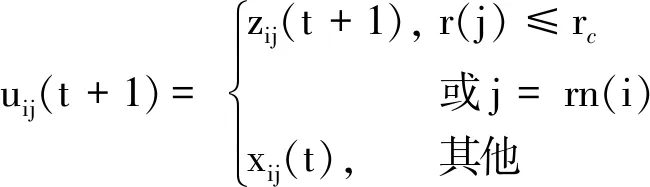
(20)

式中:xij(t)为第j个实值向量的第i个个体;zij(t)为突变向量的第j个实值向量的的第i个个体;uij(t)为交叉操作后的第j个实值向量的第i个个体;rn(j)为[0,1]中随机生成的第j个评估;rc为[0,1]内的交叉率.

为了确定向量ui(t+1)是否构成下一轮总体的个体,将其与相应的向量xi(t)进行比较.因此,如果f为最小化下的目标函数,则

(21)

步骤6更新计数器,t=t+1.

步骤7验证停止标准.若满足,则输出,否则循环到步骤3.

4 仿真结果与分析

为了验证液压执行器运动轨迹的跟踪误差,采用Matlab软件对DE算法优化的控制器进行仿真验证.仿真参数如下:种群大小为30,停止标准为100次,rc=0.8,fm=0.5,φ1=6.5× 10-18,φ2=1.5×106,φ3=1×10-10,φ4=5×106,η1=1.5×10-5,η2=1.5×10-5,Kp=5.1×109,Kd=1.9× 104,Kv=2.3×10-2.假设系统的运动轨迹方程式为

(22)

优化前的仿真结果如图4所示,优化后的仿真结果如图5所示.

图4 优化前追踪误差Fig.4 Pre-optimization tracking error

图5 优化后追踪误差Fig.5 Optimized tracking error

由图4可知,优化前液压执行器运动轨迹追踪产生的误差最大值为6.6×10-3m,误差跳动幅度较大.由图5可知:优化后液压执行器运动轨迹追踪产生的误差最大值为1.5×10-3m,误差跳动幅度较小.因此,采用差分进化算法优化液压执行器控制器,能够提高液压执行器运动轨迹追踪精度.

5 结论

针对液压执行器运动轨迹控制问题,采用了DE算法优化控制器参数,并对优化前后追踪效果进行比较,主要结论如下:

(1) 液压执行器在驱动过程中,需要液压系统和机械系统的密切配合,容易产生死区现象.

(2) 采用差分进化算法优化液压执行器控制器,能够搜索到控制器最优调整参数,从而降低运动轨迹追踪误差.

(3) 采用Matlab软件对液压执行器优化前、后的追踪误差进行仿真,能够模拟实际产生效果,避免设计不合理.