半参数空间ZISF的估计、分类与蒙特卡罗模拟
蒋青嬗,黄 灿,李毅君
(1. 广东外语外贸大学数学与统计学院,广东 广州 510006; 2. 广东工业大学管理学院,广东 广州 510520;3. 中山大学岭南学院,广东 广州 510275)
1 引言
效率衡量现有水平下生产单元获得最大产出的能力。随机前沿模型是效率测算的常用方法,得到较多理论和实证研究[1-3]。经典的随机前沿模型假定技术无效率项的分布是连续的,从而所有生产单元的技术无效率项均大于零,生产单元技术无效(技术无效率项大于零对应技术效率小于1,此时生产单元技术无效。技术无效率项等于零对应技术效率等于1,此时生产单元技术有效)。经典的随机前沿模型以及后续的拓展隐含着生产单元技术无效的前提。
Kumbhakar等[4]首次构建了零无效率随机前沿模型(Zero inefficiency stochastic frontier model,简称ZISF)。该模型属于潜在类别模型(Latent class model),包含回归模型和随机前沿模型两个分类,两类模型各有一定的发生概率且概率之和为1。其中回归模型可刻画技术有效生产单元,随机前沿模型可刻画技术无效生产单元,因此ZISF能够适用于技术有效和技术无效生产单元同时存在的情形。Kumbhakar等[4]和Abdulai和Abdulai[5]的实证分析表明,在技术无效和技术有效生产单元同时存在的情形,使用经典的随机前沿模型导致技术效率的测算不准确,ZISF有存在必要性。
目前关于ZISF的理论拓展相对较少,主要集中在模型构建和估计方面。具体可归纳为:①非参数或半参数拓展。经典的ZISF假设自变量与因变量参数线性并假设回归模型的发生概率与相应解释变量参数线性,但上述两组变量在许多情况下呈现非非线性关系。同时,经典的ZISF需事先设定生产函数(即前沿面)的形式,当函数关系不明确时容易出现函数形式误设进而影响估计结果。Yao Feng等[6]在生产函数中引入非参函数,Tran和Tsionas[7]假设回归模型的发生概率为非参函数,分别研究了目标模型的估计。②空间模型拓展。由于位置相邻、模仿、溢出和测量误差等原因,相邻生产单元极可能存在空间相关性。忽略空间效应将导致估计量有偏且不一致,技术效率的估计也将不可靠。蒋青嬗和韩兆洲[8-9]首次在ZISF中引入空间效应并研究模型估计。随机前沿模型也有相应空间拓展可以借鉴,如Kutlu[10]和Glass等[11]。③内生性拓展。经典的ZISF假设自变量与误差项不相关,该假定相对严苛。违反该假定将引发内生性,相应估计量将有偏且不一致。Tran和Tsionas[12]首次研究了ZISF的内生性,使用有限信息极大似然方法得到无偏一致估计量。④其他拓展。如Rho和Schmidt[13]完善了ZISF的检验以及估计量的渐进性质。Orea和Jamasb[14]将ZISF中的随机前沿模型的技术无效率项的分布放松为有限混合分布。目前暂无发现其他ZISF相关研究。
鉴于ZISF的理论研究相对不足且已有ZISF适用性相对较低,本文拓展ZISF模型。在ZISF中引入空间效应和非参数效应,构建了半参数空间ZISF。特别地,本文首次在生产函数和回归模型的发生概率中同时引入非参数效应,适用性更广且着重考察了不同引入方式对效率测算的影响。使用极大似然方法和JLMS法分别估计参数和技术效率,进行蒙特卡罗模拟考察方法的精度和模型的存在必要性。本文的创新之处在于:①本文模型同时引入空间效应和非参数效应。相比于经典的ZISF,本文模型能有效避免模型误设(源于引入非参数效应)和忽略空间效应导致的有偏且不一致估计量(源于引入空间效应),因此适用性更佳。②更具体地研究了非参数效应的不同引入方式对效率测算的影响。归纳现有的非参数和半参数ZISF的文献可知,已有研究分别在生产函数和回归模型的发生概率中引入非参数效应,仅简单研究了上述两类非参数效应对估计精度的影响,得出忽略非参数效应导致精度降低的结论。暂无文献研究了两种不同引入方式对精度(估计精度和分类精度)的影响程度。本文模型在生产函数和发生概率同时引入非参数效应(即引入了两类非参数效应),通过蒙特卡罗模拟考察两类效应对效率测算的影响。蒙特卡罗结果表明,忽略生产函数的非参数效应仅稍微降低参数和技术无效率项的估计精度,但忽略发生概率的非参数效应会严重降低估计精度。因此发生概率的非参数效应更不容忽视。③本文研究了目标模型的估计,为实证研究提供了严谨的分析工具。④本文模型基于面板数据且引入随时间变化的技术效率,相比于经典的ZISF适用性更佳。
2 研究设计
2.1 模型引入
Kumbhakar等[4]构建的ZISF包含两个模型:经典的回归模型和经典的随机前沿模型。回归模型发生时,技术无效率项等于零,此时生产单元技术有效。随机前沿模型发生时,技术无效率项大于零,此时生产单元技术无效。两类模型各有一定的发生概率,因此ZISF能同时度量技术有效和技术无效生产单元。在ZISF的基础上,本文构建如下半参数空间ZISF:
(1)
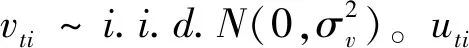
上述模型等价于:
(2)
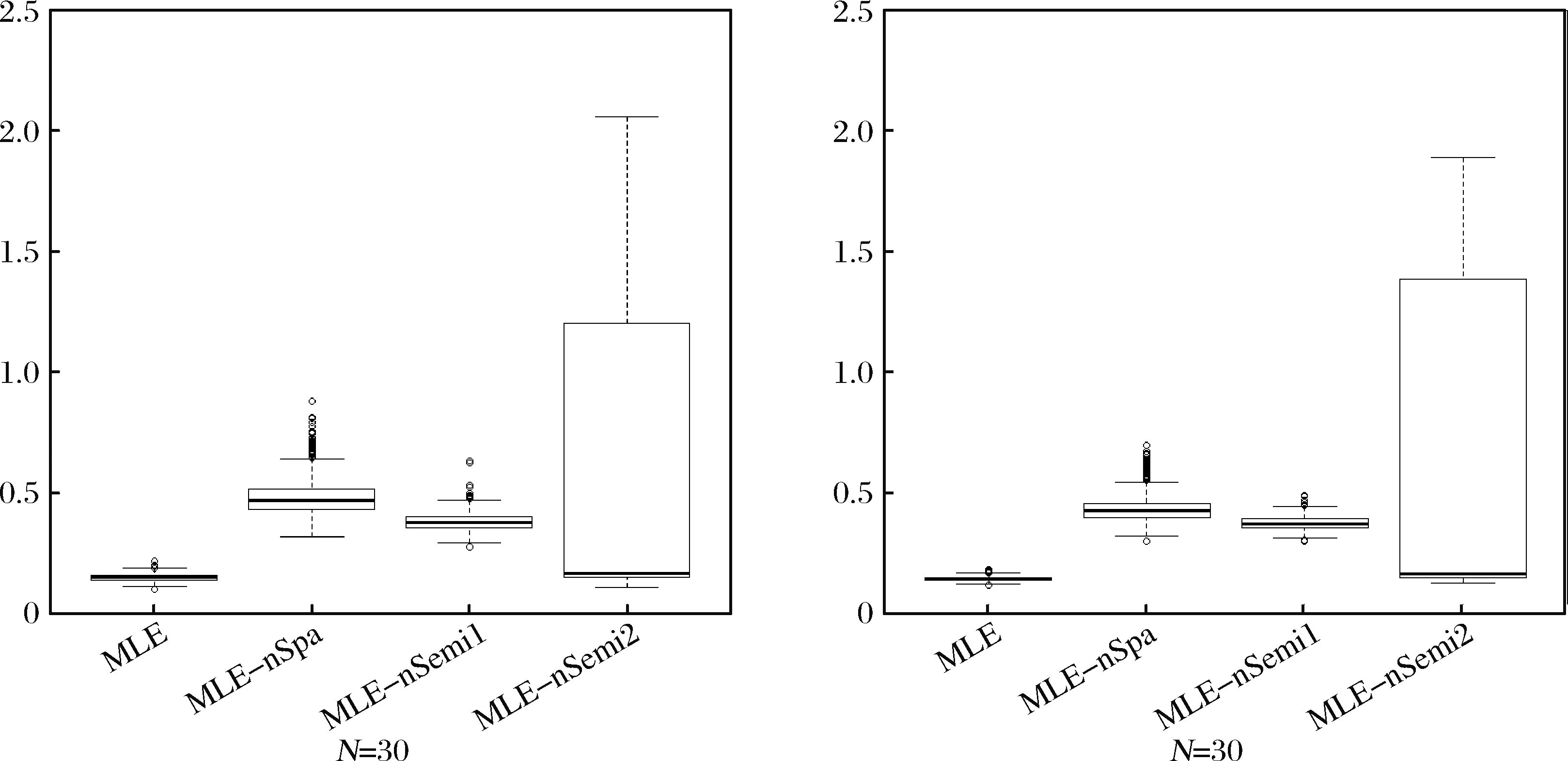
其中1{·}为示性函数,满足括号内条件即为1,否则为0。uti=0的发生概率(即回归模型的发生概率)为p(1{uti=0}=1)=f2(z2ti)。当f2(z2ti)≡0时,模型退化为经典的随机前沿模型。当f2(z2ti)≡1时,模型退化为经典的回归模型。当0 式(1)的生产函数同时包含线性关系和非线性关系,因此属于半参数模型。相比于已有的ZISF拓展模型,本文构建的模型适用性更广,具体体现在:①本文模型引入了空间效应,更符合实际情况且可有效避免忽略空间相关性导致的有偏且不一致估计量。目前ZISF的空间拓展非常少,仅蒋青嬗和韩兆洲[8-9]。②本文模型在生产函数和回归模型的发生概率中同时引入了非参数函数,共计引入两类非参数效应,适用性更佳。同类研究如Yao Feng等[6]、蒋青嬗和韩兆洲[9]仅在生产函数中引入非参数效应,Tran和Tsionas[7]仅在发生概率中引入非参数效应。而且蒋青嬗和韩兆洲[9]假设回归模型的发生概率为固定常数,极大限制了模型的适用性。本文同时研究了两类非参数效应,并在后续的蒙特卡罗模拟中研究两种引入方式对效率测算的影响。③本文模型基于面板数据,具有面板数据的优势。同类研究如Kumbhakar等[4]、Tran和Tsionas[7]均基于截面数据。 式(1)含非参数效应,此处首先进行模型转化。由于B样条在估计过程中充分利用了样本的信息,估计的精度较高,此处使用B样条估计非参函数。对于函数f1(·),参考Huang等[15]和蒋青嬗和韩兆洲[16]的设定,令z1ti有界,t=1,…,T,i=1,…,N。不失一般性,设zti∈[a,b],其中a (3) 令O1ti=(φ11(z1ti),…,φ1mn(z1ti)),τ1=(τ11,…,τ1mn)′。从而式(2)可转化为式(4),此时式(4)的生产函数已不包含非参数效应。即: (4) (5) 令εti=vti+uti(1-1{uti=0})为复合误差项。易知当uti=0时,有1{uti=0}=1且εti=vti。当uti≠0时,有1{uti=0}=0且εti=vti-uti。 当uti≠0时,推导可得此条件下εti的密度函数为: (6) 当uti=0时,推导可得此条件下εti的密度函数为: (7) 综合uti≠0和uti=0的发生概率,可得εti的密度函数为: fε(εti)=p(uti≠0)fε(εti|uti≠0)+p(uti=0)fε(εti|uti=0)=(1-f2(z2ti)) (8) 去除常数项后,模型的对数似然函数可表示为: (9) 因此式(9)可继续转化为 (10) (11) 参考Kumbhakar等[4],使用JLMS法(Jondrow等[18],取自四位作者的首字母)测算技术效率。推导可得技术无效率项基于复合误差项的条件期望为: E(uti|εti)=Euti=0|εtiE(uti|εti,uti=0)=p(uti=0|εti)E(uti|εti,uti=0)+p(uti≠0|εti)E(uti|εti,uti≠0)=p(uti≠0|εti)E(uti|εti,uti≠0) (12) 式(12)中,第三个等式的右边的第一项p(uti≠0|εti)表示已知复合误差项的情况下技术无效率项不等于零的概率,第二项E(uti|εti,uti≠0)表示已知技术无效率项不等于零的情况下复合误差项基于技术无效率项的条件期望,即为技术无效率项不等于零时技术无效率项的点估计,该点估计与JLMS点估计[18]一致。 推导可得: (13) 从而技术无效率项基于复合误差项的条件期望可表示为: E(uti|εti)= (14) 在原模型中,技术无效率项等于零的发生概率(即回归模型的发生概率)为f2(z2ti)。在得到参数的估计量后,通过贝叶斯后验概率,利用后验信息可把技术无效率项等于零的发生概率更新为p(uti=0|εti)。与式(12)的推导一致,推导可得 p(uti=0|εti)= (15) 本文假设技术无效率项相互独立,其发生概率不为固定常数且受相关外生变量影响。对于技术无效率项uti,其要么等于零要么不等于零,只有两种可能。其中等于零的发生概率为p(uti=0|εti),不等于零的发生概率为1-p(uti=0|εti)。若p(uti=0|εti)≥1-p(uti=0|εti),即p(uti=0|εti)≥0.5,有理由认为uti以更大的概率等于零,从而可把uti判定为零。否则可认为uti不等于零并把uti判定为非零。因此基于该法则可确定反向确定技术无效率项的类别(即零或非零)。 为考察方法的有效性和模型的必要性,此处进行蒙特卡罗模拟。具体数据生成过程如下: (16) (17) (18) 此处将本文方法简称为MLE,采用三种情况进行对比分析:忽略空间效应的极大似然估计(简称为MLE-nSpa),忽略非参数效应f1(·)的极大似然估计(简称为MLE-nSemi1)和忽略非参数效应f2(·)的极大似然估计(简称为MLE-nSemi2)。上述三种方法有且仅忽略一种效应。MLE-nSp忽略了空间效应,对应模型为半参数ZISF。其对数似然函数为式(10)中去除雅克比项。MLE-nSemi1忽略了非参数效应f1(·),即对非参变量z1ti不采用B样条展开。由于直接将z1ti以线性方式引入到模型会导致拟合不足,此处对z1ti采用三阶多项式样条展开。即用三阶多项式函数c1z+c2z2+c3z3逼近f1(z),其中z为非参变量的任意取值,c0,c1和c2为回归系数。该类处理在实证分析中较为常见。MLE-nSemi2忽略了非参数效应f2(·),对非参变量z2ti不采用B样条展开而直接采用三阶多项式展开,具体操作与MLE-nSemi1类似。值得强调的是,模型中含两类非参数效应,MLE-nSemi1忽略了非参数效应f1(·),但并没有忽略f2(·),对于变量z2ti仍然采用B样条展开。同理,MLE-nSemi2忽略了非参数效应f2(·),但并没有忽略f1(·),对于变量z1ti仍然采用B样条展开。本文没有研究同时忽略两类非参数效应的情形,原因在于,模拟预期MLE-nSemi1和MLE-nSemi2的估计精度较低。若模拟结果验证了该预期,忽略两类非参数效应的情形估计精度只会更差。将上述三种方法与MLE进行对比,如果估计效果远不及MLE,则文中文中模型和方法有存在必要性。为保证模拟的可靠性,模拟重复1000次。 表1 参数估计的精度 注:结果展示时将偏差、标准差和均方误差三个指标上下排列。 图1和图2分别展示了f1(·)和f2(·)的拟合曲线和真实曲线。图1中,True线呈中间高两头低的形态,左右两端各含一个波谷。MLE,MLE-nSpa和MLE-nSemi2三线与True线非常贴合,而MLE-nSemi1与True线相差甚远。图2中,True线呈中间高两头低的形态,左右两端各含一个波谷。MLE和MLE-nSemi1两线与True线非常贴合,MLE-nSpa的形态与True线相似,但在波峰和波谷附近与True线有一定差距。MLE-nSemi2与True线相差甚远。图1和图2表明,现有情况下三阶多项式样条函数无法拟合真实曲线。对于图1,N=60时MLE与True线更贴合,特别是在波峰附近。对于图2,N=60时MLE与True线更贴合,特别是在左右两个波谷附近。从而增加样本容量有助于提高MLE在非参函数的估计精度。 图1 函数f1的拟合曲线注:True线为函数f1(·)的真实曲线。 图2 函数f2的偏离程度注:True线为函数f2(·)的真实曲线。 图3展示了技术无效率项估计量与真值的偏离程度。由图3可知,MLE的箱线图位置最低且箱宽最窄,说明MLE的技术无效率项的估计精度较高。MLE-nSemi1和MLE-nSpa的箱线图位置偏高且箱宽偏宽,说明MLE-nSemi1和MLE-nSpa的技术无效率项的估计精度偏低。MLE-nSemi2的箱线图比较特殊,其1/4和1/2分位数较低,接近MLE的1/4和1/2分位数且低于MLE-nSemi1和MLE-nSpa的1/4和1/2分位数。但MLE-nSemi2的3/4和4/4分位数明显偏大(N=30时3/4和4/4分位数分别为1.2041和2.0592,N=60时3/4和4/4分位数分别为1.3872和1.8915),最终MLE-nSemi2的1/2分位数和3/4分位数之间的箱宽以及3/4分位数和4/4分位数之间的距离非常宽(N=30时MLE-nSemi2的两宽度分别为1.0388和0.8551,N=60时MLE-nSemi2的两宽度分别为1.2228和0.5043。而N=30时MLE-nSemi1的两宽度仅为0.0257和0.2295,N=60时MLE-nSemi1的两宽度仅为0.0174和0.0975)。上述分析表明MLE-nSemi2的估计精度较低,稳定性较差。对比MLE在N=30和N=60的表现可知,N=60时的箱线图位置更低且箱宽更窄,说明增加样本容量有助于提高MLE的技术无效率项的估计精度。 图3 技术无效率项的偏离程度 图4展示了技术无效率项估计量的核密度曲线,由图可知MLE-nSemi1和MLE-nSpa的核密度曲线比较接近,两者与MLE的核密度曲线形态相似但有一定的差距。MLE-nSemi2的核密度曲线与MLE差距更大,其在零附近更高耸,即在零附近取更大的概率。当样本容量增加时(N=60时),MLE,MLE-nSemi1和MLE-nSpa的核密度曲线变化不大,但MLE-nSemi2的核密度曲线在零附近的概率增加且更加偏离MLE的核密度曲线。上述结果表明,MLE-nSemi1,MLE-nSpa和MLE-nSemi2的技术无效率项的估计精度偏低,其中MLE-nSemi2的估计精度最低且稳定性最差。 表2 技术无效率项的分类准确度 表2展示了技术无效率项的分类准确度。由表2可知,当N=30和N=60时,MLE的m_all,m0和F远高于MLE-nSpa,MLE的m1略低于MLE-nSpa。MLE-nSpa的m1高于MLE的原因在于,MLE-nSpa以较大的概率把技术无效率项判定为零(图3表明,MLE-nSpa在零附近的概率高于MLE),自然而然召回率偏高。综合来说,MLE的分类精度高于MLE-nSpa。又由于当N=30和N=60时,MLE的m_all,m0,m1和F均高于MLE-nSemi1和MLE-nSemi2,从而MLE的分类准确度高于三种对比方法。对比MLE-nSemi1和MLE-nSemi2的分类精度,当N=30和N=60时,MLE-nSemi1的m_all,m1和F高于MLE-nSemi2,MLE-nSemi1的m0略低于MLE-nSemi2。综合来说,MLE-nSemi1的分类精度高于MLE-nSpa。 本文在ZISF中引入空间效应和非参数效应,构建了半参数空间ZISF,使用极大似然方法估计模型并使用蒙特卡罗模拟考察参数和非参函数的估计精度以及技术无效率项的估计精度和分类精度。蒙特卡罗模拟的结果表明: ①MLE在参数和非参函数的估计精度以及技术无效率项的估计精度和分类精度均较高。增加样本容量有助于提高MLE的估计精度。 ②对比方法(MLE-nSpa,MLE-nSemi1和MLE-nSemi2)的估计精度和分类精度均偏低,说明忽略空间效应或者非参数效应会降低估计精度和分类精度,文中模型有存在必要性。 ③MLE-nSemi1和MLE-nSemi2有且仅忽略一种非参数效应,但两种方法的估计和分类精度存在差异性。相对来说,MLE-nSemi1的估计精度和分类精度高于MLE-nSemi2,MLE-nSemi1对应估计量的稳定性也优于MLE-nSemi2。忽略生产函数的非参数效应(对应MLE-nSemi1)仅稍微降低估计和分类精度,但忽略发生概率的非参数效应(对应MLE-nSemi2)会严重降低估计和分类精度。因此发生概率的非参数效应更不容忽视。2.2 模型转化


2.3 参数估计


2.4 简化最优化步骤




2.5 技术效率的估计
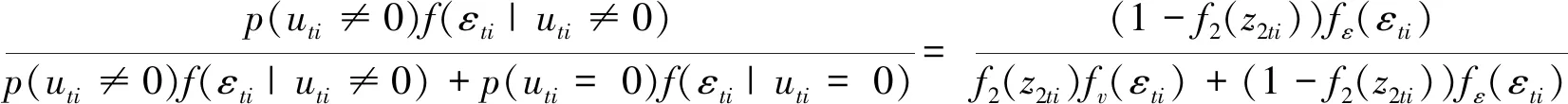
2.6 技术效率项的分类
3 蒙特卡罗模拟


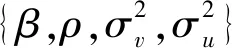






4 结语

