保证保险和产出不确定下订单农业供应链融资中的政府补贴机制
黄建辉,林 强
(1.广东农工商职业技术学院管理学院,广东 广州 510507;2.广东工业大学管理学院, 广东 广州 510520)
1 引言
订单农业是近年来出现的一种新型的先进农业生产经营模式,它不仅是中国农业产业化进程中农户与公司合作的主要形式,还是推动农业现代化的重要帮手。然而,由于农业生产的生产周期跨度较长且前期生产资料投入很多,使得订单农业合作中的农户面临巨大的生产资金压力。特别是随着订单农业在中国的深入发展,供应链中的生产资金融资难问题日益严重。如,广东湛江农垦湖光农场一位职工在冬天种植辣椒60亩而需建造御寒大棚。可是经过初步预算,大棚建造成本高达7000元/亩,即使动用多年的积蓄,仍有十几万的差额。这对于一个普通农户家庭,几乎是一笔不可负担的支出。可见,破解订单农业供应链中的融资难题,是中国订单农业生产中面临的一个现实问题。
目前,越来越多学者开始研究产出不确定下的农产品供应链。在国外,Allen和Schuster[1]采用产能优化方法来管理及缓解产出的不确定性。He Yuanjie和Zhang Jiang[2]研究随机产出下风险共担机制并得出产出随机性可提升供应链绩效。Huh等[3]讨论了产出随机性及农户违约决策。Nong Guoping等[4]及Inderfurth等[5]研究了产出不确定下的供应链协调问题。在国内,林强等[6]、叶飞等[7]都研究了农产品产出不确定下的供应链最优决策问题。凌六一等[8]分析了产出不确定下的风险共担合同对订单农业供应链各方利润的影响。可见,上述对于产出不确定性的研究,主要集中在供应链运营方面,且没有考虑资金约束问题。
随着现代农业的快速发展,也有部分学者开始研究农业供应链金融,但假设供应链不受资金约束。如叶飞等[9]提出了一种“B-S期权定价+生产协作+保证金”的合同机制来协调订单农业供应链。Zant[10]与Hosseini-Yekani等[11]为有效规避合同违约风险而提出在期货市场进行套期保值。雄峰等[12]分析不同组织模式下冷链设施补贴模式对农业供应链关系契约稳定性的影响。近年来,少部分学者研究了资金约束下订单农业供应链运营及融资决策。如,Wang Tingrui等[13]指出,订单农业供应链可以与合作伙伴进行各种形式的供应链融资,融资形式可以是订单融资或应收账款融资、存货质押融资及仓单融资。叶飞等[14]研究了由受资金约束的风险规避的农户和风险中性的公司组成的订单农业供应链的定价问题。黄建辉等[15]探讨了银行信用下受资金约束的农业企业、资金充裕的零售商及政府三者之间的供应链融资决策问题。然而,上述研究都没有考虑使用保证保险来化解订单农业供应链中的融资风险。
农业供应链中的融资难题,其实质就是银行有资金但担心放贷后的资金无法收回,即农业贷款的风险很高。核心企业担保可降低银行贷款风险[16]。近几年,学者们开始关注保证保险在规避银行贷款风险方面所起的作用。保证保险实际上是保险人起着保证人的作用,即应债权人的要求,债务人就自身的信用风险向保险公司投保。如果还贷到期后,债务人仍不能偿还债务,那么由保险公司向债权人赔偿相应的损失[17]。Williamson[18]认为,为防止机会主义而导致信用出现问题,必须预先采取各种防范措施以确保交易各方建立一个良好的信用关系。Feng Qingshui等[19]指出了作为稳定剂及助推器的农业保险的重要性。Mahul[20]、Ranganathan等[21]研究了通过购买保险的方式来对冲农产品的价格波动风险。杨霞和李毅[22]认为,作为一种融资型风险转移方式的农业保险,可提升我国农业自然灾害风险管理能力。另外,中国政府也重视保证保险在农业中的应用,如2017年中央一号文件提出,要扩大银行与保险公司合作,发展保证保险贷款产品。山东寿光市金融办正在探索如何向订单农业企业和农户提供贷款保证保险服务的问题[23]。
本文是在上述文献研究的基础上,根据农业生产特性及现实情况,进一步假设农户会受资金约束及农产品产出的不确定性,分析了受资金约束的订单农业供应链融资中的政府补贴机制设计问题。同时,为了减轻农户的贷款压力及降低银行的贷款损失风险,本文还引入了政府补贴下的贷款保证保险,构建了政府、银行、公司、农户的四阶段Stackelberg动态博弈模型,并分析了政府补贴对供应链各合作伙伴最优决策的影响。最后,得到了社会福利最大化下的政府补贴机制。此外,本文还将理论研究与实践应用相结合,对目前政府正推广的“政银保”合作贷款新模式进行了案例分析,并提出了改进建议。以上研究,不仅可完善和丰富供应链融资理论,还可为政府制定相关补贴机制和改进“政银保”提供一定的理论参考和实践指导。
2 基本模型构建
2.1问题描述
在由受资金约束的单一农户与资金充裕的单一公司组成的订单农业供应链(如图1)中,农户生产单一农产品并全部被公司收购,同时公司对所收购的农产品进行简单加工后再销售消费者。

图1 订单农业供应链结构模型
类似于Jing Bing和Seidmann[24]的研究,设农户的初始资金为零。因此,为满足生产资金需求,农户必须向银行借款。另外,政府一方面为了提高银行向无资产抵押的农户放贷的积极性,帮农户购买了贷款保证保险(当农户不能偿还贷款时,由保险公司承担偿还责任,以降低银行信贷风险);另一方面还补贴农业贷款利息,以此来减少农户还贷压力。
供应链融资系统主要由农户、公司、银行、政府、保险公司和消费者构成,具体如图2所示。
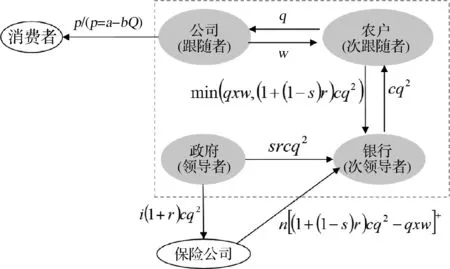
图2 基于政府补贴的订单农业供应链决策系统
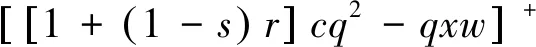
本文以保证保险支持下政府补贴贷款利息为背景,构建了订单农业供应链融资中的四阶段动态博弈模型:(1)政府、银行、公司、农户四方进行两主两从的Stackelberg博弈。政府与银行分别是领导者(Leader)与次领导者(Sub-leader),而公司与农户分别是跟随者(Follower)与次跟随者(Sub-follower)。(2)Stackelberg博弈共分四个阶段:第一阶段为政府确定贷款利息的最优补贴率s*;第二阶段为银行确定最优贷款利率r*;第三阶段为公司确定最优收购价w*;第四阶段为农户确定最优生产投入量q*。
2.2 基本假设及参数设置
在构建模型之前,对参数设置进行说明,并进一步提出以下假设。
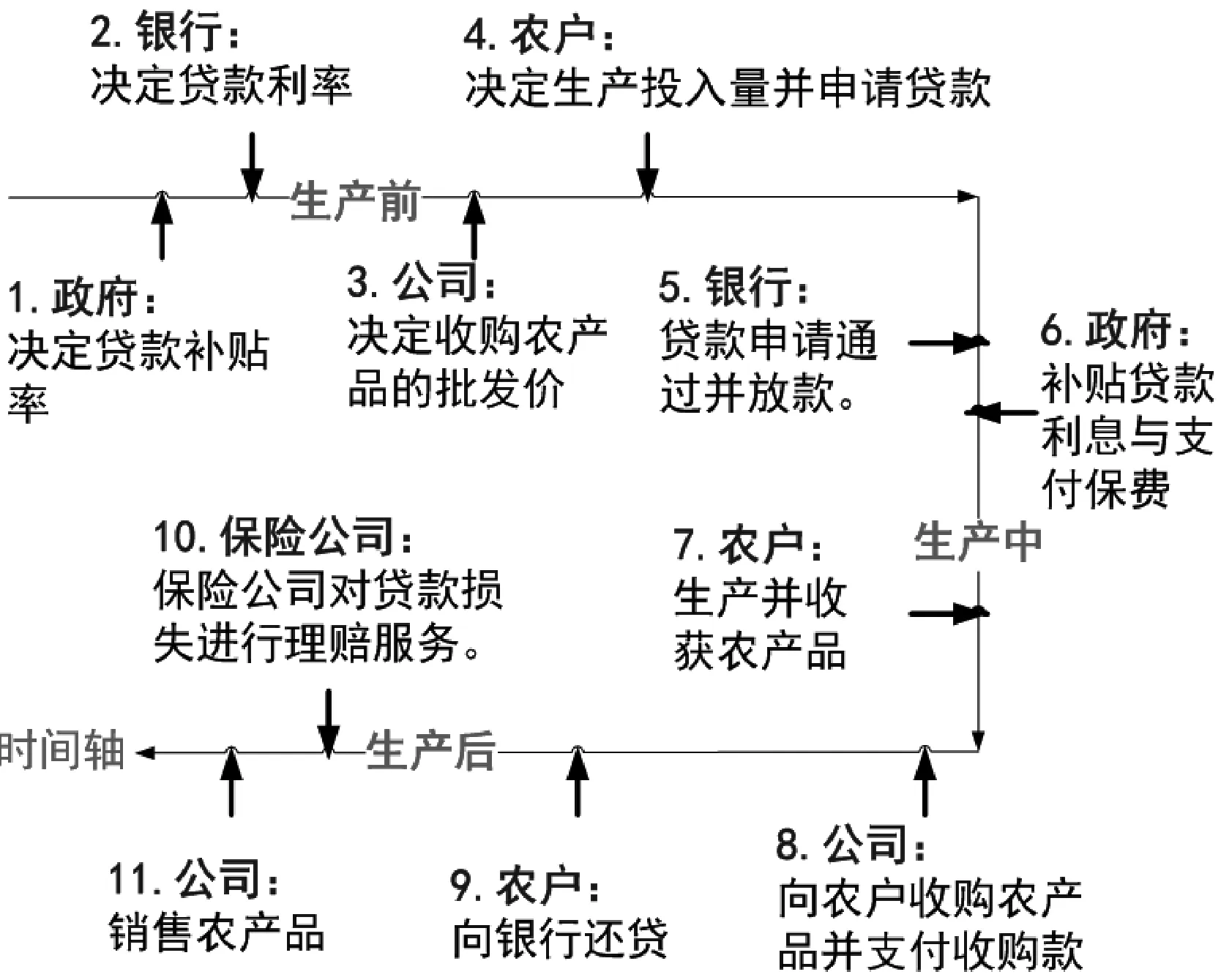
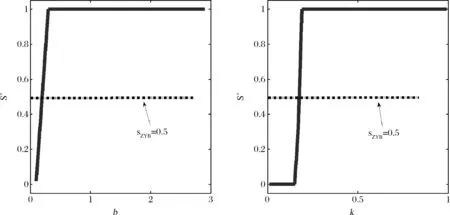
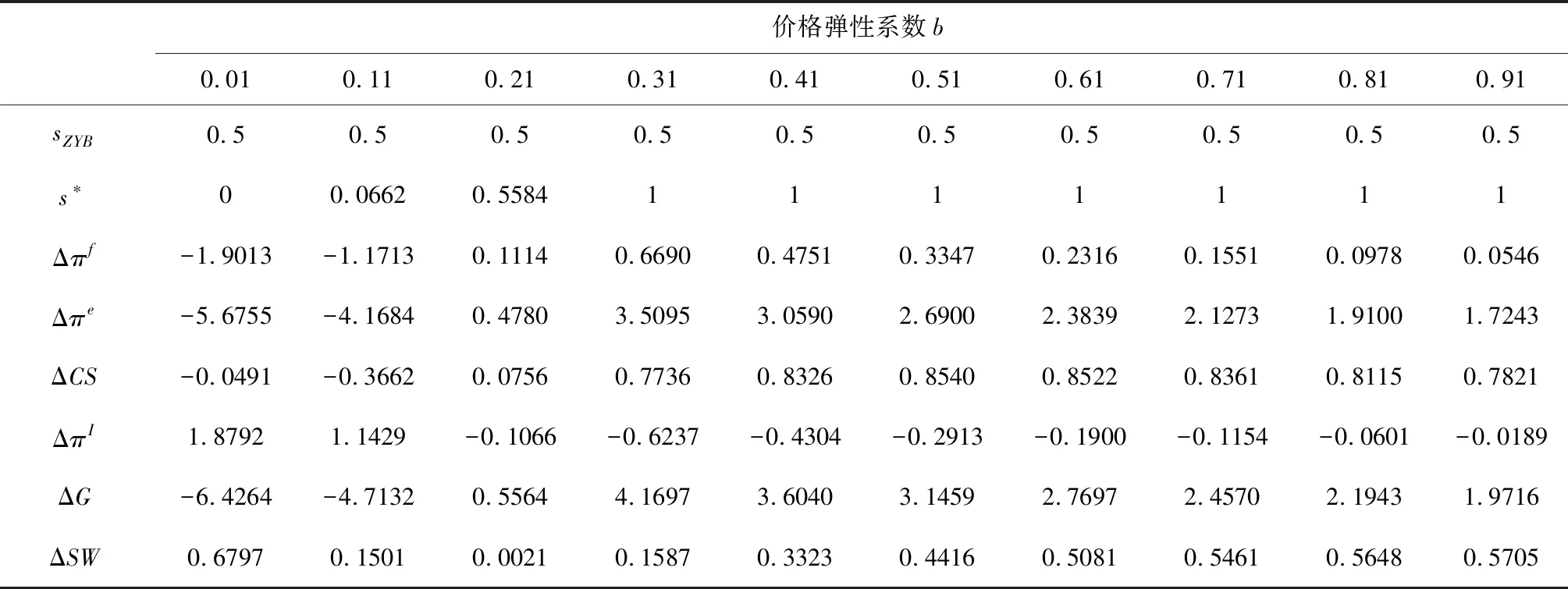
(1) 由于农产品生产易受各种异常天气以及病害虫等自然灾害等影响,故农产品的生产年份可分为两种年份,即“丰收年”和“灾害年”。在丰收年,农户可获得生产的丰收;而在灾害年,生产产量低下。不失一般性,设丰收年发生的概率为k(0 (2)设产出不确定性下的农产品投入产出率x为离散随机变量,其离散点为xH与xL(xL (3)农业生产存在着规模的不经济[25]。一个对农业生产规模不经济性的合理解释是,生产方的产能有限,当生产量增加到一定程度时,其边际成本必增加[26]。因此,二次型函数C(q)=c1q+cq2是众多学者设置农业生产成本的普遍做法[7,27],其中c1表示生产单位农产品所需投入的生产成本,如购买种子、化肥、农药等农业生产资料,c为农户在农产品生产过程中的努力成本系数。据此,本文也假设农业生产成本函数为C(q)=c1q+cq2。同时,为简化计算且不影响一般性,设c1=0。 (4)借鉴Jing Bing和Seidmann[24]、Kouvelis[28]和Zhao Wenhui[29]、Jing Bing等[30]、Yan Nina等[31]的做法,假设银行进行着完全市场竞争(Perfectly competitive market)下的伯特兰德(Bertrand)价格博弈。 (5)假设不考虑农户与公司双方的道德风险,即双方都不会违约。 (6)上标f、e、b、i分别代表农户、公司、银行和保险公司,“*”表示最优解。 订单农业供应链完成一个生产与销售周期的博弈顺序与详细过程为: ①政府首先决定贷款利息补贴率s,并承若为农户购买贷款保证保险。②银行根据政府公布的s,决定贷款利率r。③公司根据给定的s及r,决定农产品的收购价w。④农户再根据政府、银行、公司的决策,确定农产品的生产投入量q。另外,农户还需根据q来预估可能发生的生产成本cq2,并向银行申请贷款。⑤银行审核贷款申请后,以贷款利率r向农户放款。⑥政府履行承若,支付贷款利息补贴srcq2给银行,以及支付保险费i(1+r)cq2给保险公司。⑦农户在收到贷款资金后,开始生产,并最终收获数量为qx的农产品。⑧公司收购农产品,并向农户支付收购款qxw。⑨农户收到收购款后,优先还贷。如能还清贷款,则结余为农户所得利润;否则农户破产。可知,农户能还贷的金额为min(qxw,(1+(1-s)r)cq2)。⑩保险公司对于银行贷款损失进行理赔,理赔额为n[(1+(1-s)r)cq2-qxw]+。最后,公司对农产品进行简单加工(如清洗)后,进行销售并获得货款pqx。 具体时间序列博弈过程如图3所示。 本文中的农户破产, 是指农户承担有限责任[26]。在订单农业中,农户往往是能进行规模化种植的新型农业经营主体,比如家庭农场等,因此具有法人资格并可承担有限责任。如,湖北黄冈市一位农民在工商局拿了“家庭农庄”的营业执照,从自然人转变为经工商登记的法人。借鉴Jing Bing等[30], Chen Xiangfeng等[32]对破产处理的做法,当 图3 供应链融资的时间序列决策过程 农户的农产品收购款不足以偿还贷款本金及利息时,农户会破产;破产后的贷款余额不用再偿还,由此造成的贷款损失由保险公司和银行共同承担。 据以上分析,可分别得到农户、公司、银行的期望利润函数(与政府相关的决策放在“3.5政府的最优补贴率决策”节中集中讨论,故其决策函数在本节中未论述)。 农户的期望利润函数为: (1) 式(1)中,y+=max(0,y)。qxw为农户所得的农产品收购款。cq2为贷款本金,(1-s)rcq2为需支付给银行的贷款利息。 公司的期望利润函数为: s.t.w≤p (2) 式(2)中,pqx为公司销售农产品所得的销售款,其中p=a-bqx。不失一般性,令w≤p。 银行的期望利润函数为: s)r)cq2)+n((1+(1-s)r)cq2-qxw)++srcq2-cq2] (3) 另外,由于灾害年和丰收年的农产品投入产出率不同,对于同样的生产投入,会获得高、低不同的两种农产品产出,其中低的产出可能致使农户无力偿还银行债务而破产。因此,根据农户贷款后是否存在破产风险,可分三种情形:情形①为农户不存在破产风险(即使是遇到灾害年,农户也不会破产);情形②为农户存在破产风险(若遇到丰收年则不会破产,若遇到灾害年则会破产);情形③为农户肯定破产(即使遇到丰收年,农户也会破产)。考虑简化运算及现实背景,本文假设农户是在情形②下从事农业生产活动。 图3中博弈顺序中的1、2、3、4步骤,即对应为Stackelberg博弈的第一、第二、第三及第四阶段,其也是博弈四方(政府、银行、公司、农户)决策的先后顺序。因此,接下来将采用逆向归纳法分别求解各自的最优解,即先求解博弈第四阶段的农户最优生产投入量q*,接着求解博弈第三阶段的公司最优收购价w*,然后求解博弈第二阶段的银行最优贷款利率r*,最后求解博弈第一阶段的政府最优补贴率s*。 再由式(1),可将农户期望利润函数简化为: (4) 易知πf(q)为q的严格凹函数,故可得定理1。 定理1在保证保险和产出不确定下的订单农业供应链融资中,如果给定贷款利息补贴率s,银行贷款利息r,以及公司收购价w,那么农户的最优生产投入量为: q*=ηw (5) 将p=a-bqx代入式(2)中,化简可得公司的期望利润函数为: πe(w)=q(aμ-μw)-bq2φ s.t.w≤a-bqμ (6) 定理2在保证保险和产出不确定下的订单农业供应链融资中,如果给定贷款利息补贴率s与贷款利息r,那么公司的最优收购价为: (7) 根据3.1中的约束条件(1)与约束条件(2),对式(3)进行化简,可得银行的期望利润为: πb(r)=krcq2+(1-k)[qxLw+srcq2-cq2+n((1+(1-s)r)cq2-qxLw)] (8) 由于银行是处于完全市场竞争下的Bertrand价格博弈,故可知式(8)πb(r)=0,再联合式(5)、式(7),对式(8)进行处理,可得: 定理3在保证保险和产出不确定下的订单农业供应链融资中,如果给定贷款利息补贴率s,那么银行最优贷款利息为: 在定理3中,为何最优贷款利率可能等于零。其原因是,当xH/2≤xL时,无论是遇到丰收年还是灾害年,农户都有能力还清贷款。此时银行不存在贷款损失风险,而处于完全市场竞争下Bertrand价格博弈的银行,在不考虑无风险利率(Risk-free interest rate)的情况下,其边际成本为零[31],故银行会设置贷款利率为零。 另外,从定理3易知,当xH≤2xL时,r*=0,而当xH>2xL时,r*>0,故农户需要政府补贴贷款利息。因此,可得推论1。 推论1 当xH≤2xL时,政府无须提供补贴机制;否则,政府应提供补贴机制。 推论1说明,当丰收年投入产出率不超过灾害年投入产出率2倍时,政府无须提供针对贷款利息的补贴机制;否则,政府应提供补贴机制。 据此,如无特殊说明,以下都是讨论xH>2xL条件下的政府补贴对供应链各方最优决策的影响,以及政府补贴机制的设计问题。 由定理1、定理2、定理3,可得如下定理。 定理4在保证保险和产出不确定下的订单农业供应链融资中,当xH>2xL时,如果给定政府补贴率s,那么农户最优生产投入量q*、公司最优收购价w*,银行最优贷款利率r*分别为: (9) (10) (11) 推论2 农户最优生产投入量是政府补贴率的增函数,而公司最优收购价与银行最优贷款利率都是政府补贴率的减函数。 在推论2中,直觉会认为政府增加补贴,银行应该提高贷款利率,以占用更多政府资源。但推论2却给出了相反结论。这是因为,政府补贴可降低银行信贷风险,即相当于减少了信贷成本,从而降低了边际成本,故在伯特兰德(Bertrand)价格竞争中,银行贷款利率也会跟着下调。 将式(9)、式(10)和式(11)分别代入到式(4)与式(6)中,可得农户与公司的最优期望利润依次为: (12) (13) (14) 推论3πf*是关于s的严格凹函数,且s′是πf*的极大值点,其中s′是由式(14)确定。 从推论3可知,政府对农业贷款的补贴越多,对农户不一定更有利。 推论4πe*是s的严格递增函数。 推论4说明公司一直会受益于政府的补贴。 众所周知,政府财政资金是属于社会公共资源。因此,政府要从社会整体利益出发,通过补贴农业贷款利息,以激励各合作伙伴为社会创造更多价值,并实现社会福利的最大化,即政府应从社会福利最大化角度来设置最优补贴率。而社会福利是由生产者剩余和消费者剩余构成,即由订单农业供应链各方(农户+公司+银行+保险公司+消费者)利益所组成。农户、公司、银行及保险公司属于经营实体,故上述四者以期望利润代表各自利益。消费者以消费者剩余来衡量其利益。另外,社会福利还需扣除政府支付的保险费及贷款利息补贴。据以上分析,可得社会福利函数为: (15) 式(15)中,πf(q)、πe(w)、πb(r)分别代表农户、公司、银行的期望利润,且分别由式(4)、式(6)与式(8)决定;πI代表保险公司的期望利润,CS代表消费者剩余,i(1+r)cq2与srcq2分别代表政府支出的保险费与贷款利息补贴额。 πI= (16) 同样,由于农户只有在灾害年才会破产,即保险公司只有在灾害年才会发生贷款保证保险赔偿款的理赔,故式(16)经整理后为: πI=i(1+r)cq2 -(1-k)n((1+(1-s)r)cq2-qxLw) (17) (18) 将式(4)、式(6)、式(8)、式(17)、与式(18)代入到式(15)中,可得: (19) 再根据式(19),不难得出∂2SW/∂q2<0,故可得引理1。 引理1 社会福利SW是q的严格凹函数。 (20) 由式(20),可得定理5。 1.当b≥2c/φ时 由引理2,再结合由推论2中的∂q*/∂s>0,可得定理6。 定理6当b≥2c/φ时,如果政府从社会福利最大化角度出发,那么政府应对贷款利息进行全额补贴,即政府的最优补贴率s*=1。 结合引理2与定理6,可知,在一定条件下,政府即使通过补贴机制,也不可达到社会福利最大化的标杆水平。但政府可通过设置补贴率来提升生产投入量,以尽可能地增加社会福利。 2.当b<2c/φ时 (21) 由于最优补贴率s″还需满足约束条件0≤s″≤1,即SW*的极大值点s″并非一定是最优补贴率的可行解。 因此,根据s″≥0与式(21),可得引理3。 再根据约束条件s″≤1与式(21),可得引理4。 定理7在保证保险和产出不确定下的订单农业供应链融资中,如果政府从社会福利最大化的角度出发,那么政府的农业贷款补贴机制应满足: 从定理7不难得出,政府对农业贷款利息补贴力度的变化趋势是,随着价格敏感系数b的增大,政府补贴也会随之增加。具体表现为,当b小于一定值时,政府不应提供补贴,即s*=0;当b适中时,政府应提供补贴,即s*>0;当b大于一定值时,政府应提供全额补贴,即最s*=1。 推论5 在保证保险和产出不确定下的订单农业供应链融资中,如果政府从社会福利最大化的角度出发,那么有: 以下将结合上述的理论研究成果,通过数值分析得出“政银保”合作贷款新模式(以下简称“政银保”)对供应链各方的影响,以及探讨该模式未来的改进建议。 4.1.1 “政银保”合作贷款新模式简介 “政银保”是国内首例经过保监会审批了的合作农业贷款模式。它是一种建立以政府农业产业政策为导向、以银行贷款为基础、以保证保险为保障、以政府基金作担保的分散风险和有效控制的新型融资产品。该模式开创政府引导,保险、银行共同参与的融资新模式,实现了政府、银行、企业和保险公司多方共赢。“政银保”缓解农户融资难、融资贵难题,提高了银行放贷的积极性。因此,“政银保”是农村金融综合改革创新的一项重要举措,更是普惠农村与农民的民生工程。 “政银保”最初在2009年由广东省佛山市三水区开始试点。随后该农业融资模式在广东省及全国得到了较大的推广和应用。2014年,广东省政府将“政银保”列入农村普惠金融“八项行动”之一。从2014年开始,以4年为一个周期,广东省财政每年安排5000万元贷款扶持资金,实施 “政银保”项目,为农业贷款对象全额补贴保费(保费费率一般为2%)、补贴50%的贷款利息。 “政银保”执行的是由政府、银行、保险三方分层共担风险的模式。风险共分为三层:当贷款本金发生损失,(1)第一层:如果在规定150%保险赔付之内,由银行和保险公司共同承保贷款损失责任,其中保险公司承担80%贷款损失,而银行承担20%。(2)第二层:如果超过150%的保险赔付封顶线,但在政府兜底基金之内的贷款损失,保险公司首先支付150%的赔偿金,然后由银行和政府再共同承担剩余超赔部分的责任,其中政府扶持基金负责80%,而银行负责20%。(3)第三层:如果达到保险赔付封顶线及用完政府的超赔基金后,由银行单独承担其后的贷款损失风险。 另外,来自人保财险广东分公司五年经营数据,可知,至今未发生过需要动用政府兜底基金的情形,即第二层与第三层风险从未有发生过[33]。因此,实际中,“政银保”贷款损失风险由保险公司与银行共同承担,此情况与本文假设一致。 4.1.2 “政银保”合作贷款新模式的补贴率分析 从4.1.1节中,可知“政银保”固定的贷款利息补贴率sZYB=0.5,保险费率i=0.02,n=0.8为保险公司承担损失的百分比。其他参数取值如下:销售市场规模a=1000,价格弹性系数b=1.1,丰收年发生概率k=0.3,丰收年与灾害年的投入产出率为xH=15、xL=3,努力成本系数c=90。 首先进行“政银保”补贴率sZYB与政府最优补贴率s*的对比分析,如图4所示。从图中不难发现,s*会受价格弹性系数b或丰收年发生概率k的影响。而“政银保”设置固定的补贴率不一定是最好,如当b较小时,政府补贴不但不能给社会福利带来好处,甚至还可能不利于社会福利。 4.1.3 “政银保”对供应链合作伙伴的影响分析 表1对比分析了“政银保”下补贴率(sZYB=0.5)与政府补贴机制下的最优补贴率s*对订单农业供应链各合作伙伴的利益影响。 根据表1,易发现,相对于政府补贴机制,(1)当b很低时,虽然“政银保”可带给农户、公司及消费者更多利益,但他们的获益是通过巨大政府补贴而得到的。如当b=0.01与b=0.11时,政府补贴差值分别为ΔG=-6.4264、ΔG=-4.7132,同时 ΔSW=0.6797、ΔSW=0.1501。可见,“政银保”下的农户、公司及消费者获利是以社会福利的损失为代价。(2)当b不是很低时,“政银保”除了有利于保险公司外,对包括社会福利、农户、公司、消费者在内的供应链各方都不利。(3)另外,随着b递增,由于公司可控制收购价,使得公司是政府补贴机制下的最大受益者,而农户虽然从中受益但获益较小,保险公司甚至亏损。 图4 最优补贴率s*与“政银保”补贴率sZYB对比分析 表1 “政银保”下固定补贴率与政府补贴机制下最优补贴率对各方影响分析 价格弹性系数b0.010.110.210.310.410.510.610.710.810.91sZYB0.50.50.50.50.50.50.50.50.50.5s∗00.06620.55841111111Δπf-1.9013-1.17130.11140.66900.47510.33470.23160.15510.09780.0546Δπe-5.6755-4.16840.47803.50953.05902.69002.38392.12731.91001.7243ΔCS-0.0491-0.36620.07560.77360.83260.85400.85220.83610.81150.7821ΔπI1.87921.1429-0.1066-0.6237-0.4304-0.2913-0.1900-0.1154-0.0601-0.0189ΔG-6.4264-4.71320.55644.16973.60403.14592.76972.45702.19431.9716ΔSW0.67970.15010.00210.15870.33230.44160.50810.54610.56480.5705 4.1.4 “政银保”合作贷款新模式的改进建议 政府是通过国家财政来激励各方多为社会做贡献,并带来更多社会福利。因此,对“政银保”的改进建议是:(1)政府应该根据实际情况采取不同的最优补贴率,而不应使用固定不变的补贴率以确保社会福利的最大化。(2)当b较小时,政府应提供少量补贴甚至是不应提供补贴。(3)当b较大时,由于政府补贴机制一直对公司非常利,农户却获益不大,且不利于保险公司。此外,“政银保”中的保险公司利润与风险不匹配。如保险公司按贷款金额2%左右收取保费,但却需承担80%的损失,使得保险公司保证保险业务处于盈亏平衡状态,甚至是亏损。 因此,“政银保”实施中还应增加保护弱势群体的条款:①要求提高收购价或收益二次分配等方式来保护农户利益;②贷款保证保险更多地投向中低收入人群、个体户及小微企业,如针对具有稳定工作和还款能力的中低收入农户,且月收入3000元以上,承保金额可为2~15 万元人民币;③推动建立风险补偿机制,通过适当提升补偿比例,降低银行及保险公司承担的风险;④推动优化保险公司与银行损失分担比例,如银行与保险公司承担贷款损失风险比例优化为3∶7,以提高保险公司参与的积极性。 本节中,相关参数取值与4.1一致。 农户及公司的最优期望利润与政府补贴率s之间的变化趋势如图5所示。从图5 可得出,农户的最优期望利润是关于补贴率的凹函数,而公司的最优期望利润是随着补贴率的递增而递增。上述现象说明,政府对农业贷款的补贴越多,对农户不一定更有利,但政府补贴一直有利于公司。上述现象验证了推论3与推论4的结论。 图5 补贴率对农户及公司的最优期望利润影响 本节中,相关参数取值与4.1一致。 图6 价格弹性系数变动对最优补贴率的影响分析 本文研究了由单一农户与单一公司组成的订单农业供应链,其中农户受资金约束。考虑农产品产出的不确定性及贷款保证保险,构建了政府、银行、公司与农户的四阶段Stackelberg动态博弈模型,同时分析了政府补贴对供应链各方最优决策的影响,并得到了社会福利最大化下的政府补贴机制。最后,将理论研究与实践应用相结合,对“政银保”合作贷款新模式进行案例分析,并进一步提出了改进建议。 研究发现,(1)农户的最优生产投入量是政府补贴率的增函数,而公司最优收购价与银行最优贷款利率却都是政府补贴率的减函数。(2)农户最优期望利润是关于政府补贴率的严格凹函数,而公司的最优期望利润是政府补贴率的严格递增函数。(3)当丰收年的投入产出率不超过灾害年的投入产出率2倍时,政府无须提供补贴机制;否则,政府应提供补贴机制。(4)社会福利最大化下的政府补贴机制应为:①当价格敏感系数小于一定值时,政府不应提供补贴;②当价格敏感系数适中时,政府应提供补贴;③当价格敏感系数大于一定值时,政府应提供全额补贴。④特别地,当灾害年与丰收年的投入产出率比值提升到一定值时,最优补贴率不受价格敏感系数的影响,政府应提供部分补贴。甚至当投入产出率比值提升到更大值时,政府应提供全额补贴。⑤对“政银保”的改进建议:政府应该根据实际情况采取不同补贴率,而不应使用固定补贴率。当价格敏感系数较大时,应设置保护农户的最低收购价等配套策略。 政府有时在设计补贴机制时,还受财政资金约束的限制,或者是希望以最小的成本获取最大的价值,这是下一步的研究方向。2.3 基本模型
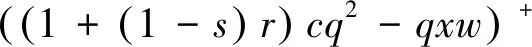
3 保证保险下的供应链最优决策
3.1 农户的最优生产投入量决策(博弈第四阶段)
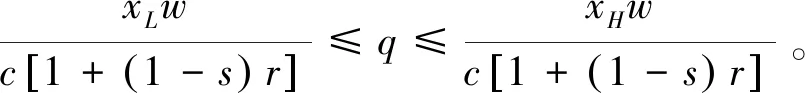
3.2 公司的最优收购价决策(博弈第三阶段)
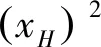

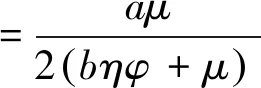

3.3 银行的最优贷款利率决策(博弈第二阶段)
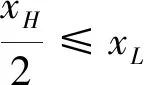

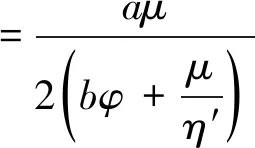
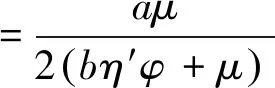

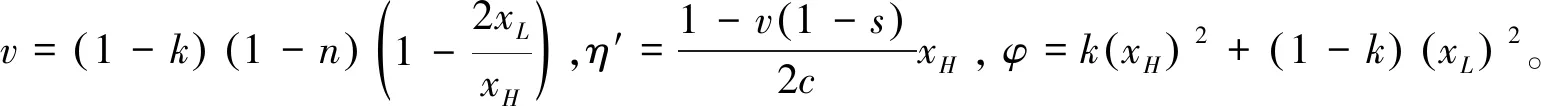
3.4 政府补贴对供应链合作伙伴决策影响分析
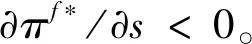
3.5 政府的最优补贴率决策(博弈第一阶段)
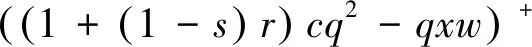
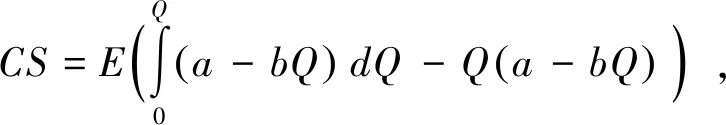
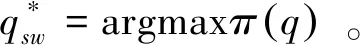
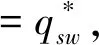
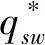

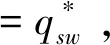

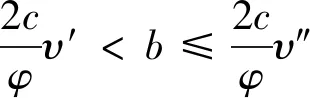
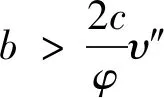

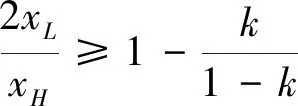
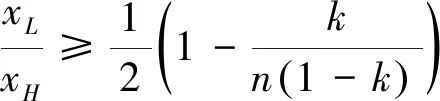

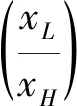
4 数值分析
4.1 “政银保”合作贷款新模式的案例分析
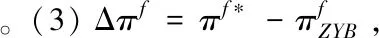
4.2 政府补贴率对农户与公司期望利润影响分析
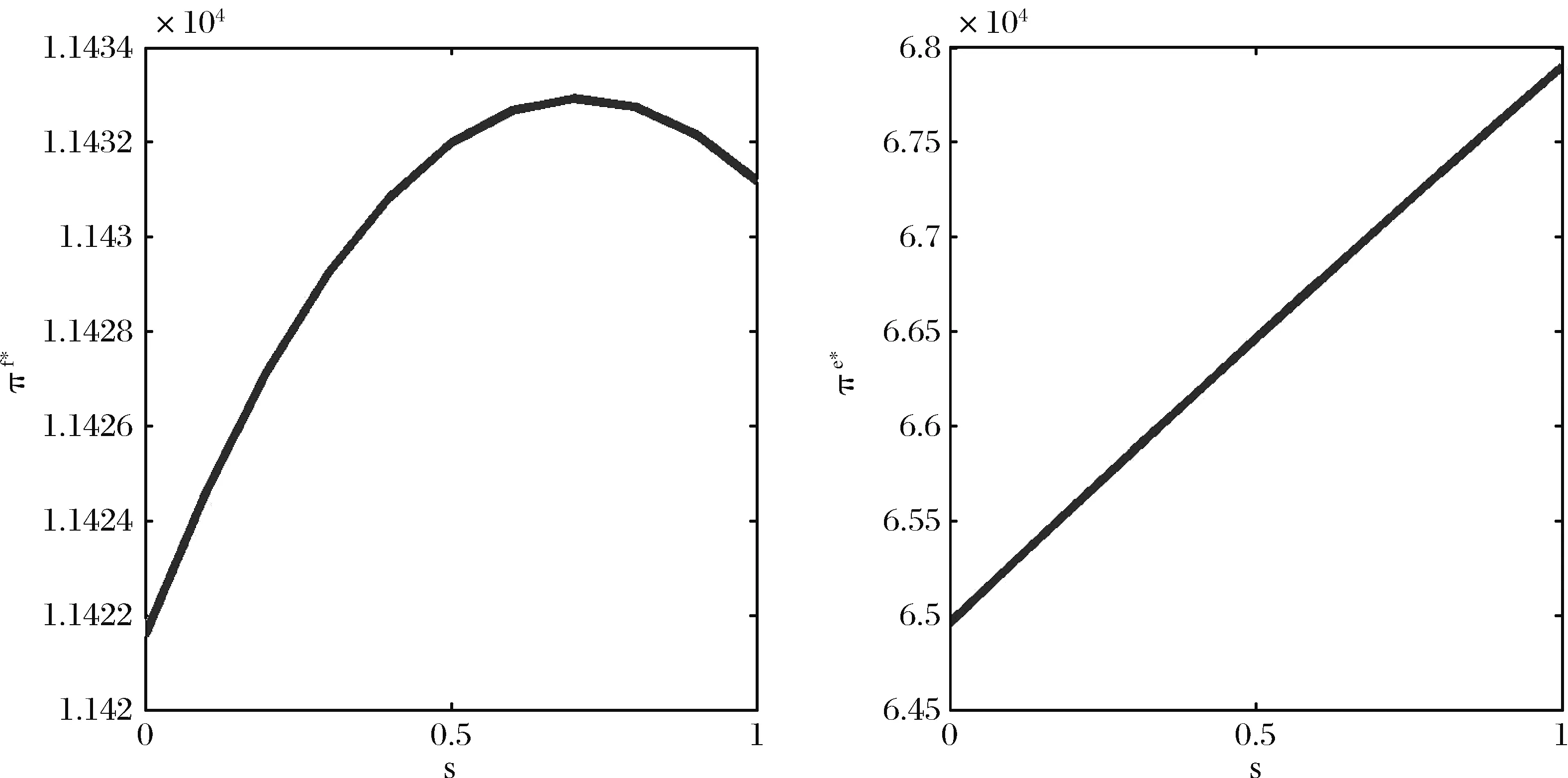
4.3 价格弹性系数对最优补贴率的影响分析

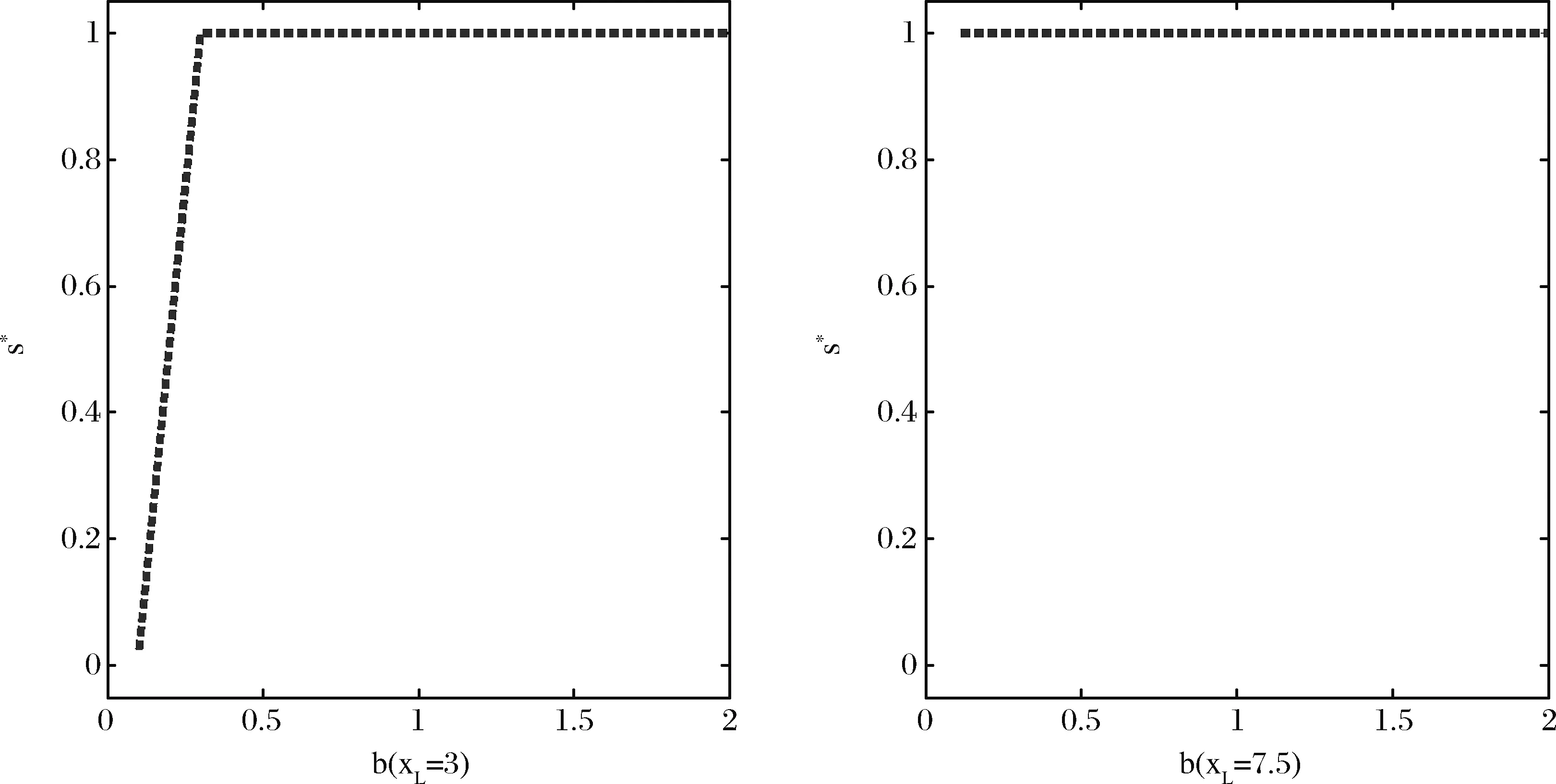
7 结语

