基于LED光谱匹配方法的任意光谱拟合研究*

张从征，许毅钦，古志良，郭 亮

1.华南师范大学信息光电子科技学院，广东 广州 510631；2. 广东省半导体产业技术研究院，广东 广州 510650

发光二极管(LED)作为新一代固态照明光源，以其光效高、体积小、寿命长、节能环保、控制灵活等优点逐渐应用到照明、背光等领域，被誉为最具应用前景的照明光源之一[1-2].LED光谱作为其光度色度特性研究的基础，近年来得到了国内外学者越来越多的关注与探究.虽然普通白光LED的应用非常广泛，但在一些特殊照明领域，如健康照明、植物照明，太阳光模拟器[3]等，单一LED的光谱并不能满足生产要求，此时便需要通过多种单色LED进行混光来合成所需的目标光谱.美国国家标准与技术局(NIST)最先于2006年研制了一款光谱可调的积分球光源[4].该积分球光源内部安装有多个不同波段的LED光源，通过单独控制每个LED的电流大小，得到不同的光谱分布，进而实现与目标光谱的匹配.

LED光谱匹配算法主要基于光谱叠加原理，多个LED混光后的光谱曲线为每个LED光谱曲线线性相加之和.因此，可以通过调节LED光源的种类、数量、驱动电流来改变最终合成的光谱，完成对光谱的匹配.国内外已有许多关于光谱数学模型及光谱匹配方面的研究.2010年，朱继任等[5]采用非对称的高斯分布函数拟合单个LED光谱分布，并以该数学模型为基础，使用多个不同峰值波长的单色LED实现了对任意光谱的合成，得到了较理想的拟合结果.后来，甘汝婷等人[6]对匹配算法进行了改进，他们以简单遗传算法作为光谱匹配算法，通过求解超定方程组的非负最小二乘解，实现了多个单色LED对CIE-D65标准光源、AM1.5标准太阳光目标光谱的再现.2017年，徐广强等人[7]提出用光子在二维空间内联合态密度函数作为单色LED的光谱辐射模型，建立LED光谱拟合数据库，通过优化不同峰值波长、半高宽的单色与白光LED组合，实现对目标光谱的匹配.从以上研究我们可以看出，目前拟合采用的光谱是由数学模型建立的，算法比较复杂，虽然模型在不断改进，但与实际的光谱曲线仍存在误差，并且对荧光粉模型拟合的精度欠佳.

本文提出一种基于实测光谱信息的LED光谱匹配方法，首先对LED光源进行测试并建立LED光谱数据库，根据匹配选用的LED个数，使用Matlab编程软件列出数据库中所有的光谱组合，通过拟合计算实现对目标光谱的匹配.相比于以往研究中构造的数学模型，该方法通过对光谱实测建立数据库，算法简单，拟合结果可直接应用，更加切合实际，对健康照明、植物照明等特殊照明领域的光谱匹配有一定的实践指导意义.

1 光谱匹配技术

1.1 光谱叠加原理

在科学实验和工程应用中，曲线拟合是对目标做出预测或结论的重要手段，最小二乘法作为曲线拟合中最常用的一种回归算法，因其简单方便、运算效率高，广泛应用于众多学科的数据分析.考虑到本文的实际情况，选用最小二乘法进行拟合运算.

实际应用中的LED光源光谱往往是非常丰富的，如一些高精度的太阳光模拟器包含近百种的LED.因此，单个LED光谱不足以对目标光谱进行匹配，运用光谱匹配算法可以很好地解决这个问题.利用迭代法计算出多个LED线性叠加后的光谱与目标光谱的最小差异，得到当前使用的LED种类及对应的比例，且驱动电流与光谱相对能量近似为正比的关系，利用计算结果便可通过调节电流实现光谱匹配[8].由光谱叠加原理可得LED光谱合成的数学模型为:

(1)

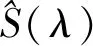
虽然实际的光谱是连续的，但由光谱仪实测的光谱为一系列与波长对应的离散点数据，在可见光范围内等间隔选取401个离散点表示一个光谱数据，假设目标光谱的数据为：

L(λ)=[y380,y381,y382,y383,…,y780]T.

(2)

数据库中LED数据表示为：

S(i)=[S1(λ),S2(λ),S3(λ),S4(λ),…,Si(λ)].

(3)

式(3)中Si(λ)为光谱数据库中第i种LED的光谱数据，假定系数矩阵k=[k1,k2,k3,k4,…ki]T，可得拟合计算公式：

S(i)×k=L(λ).

(4)

由于匹配选用的LED个数i<401，故此方程组为超定方程组.在古典意义下此方程组是无解的，但可以求其广义解.在实践应用中LED个数只能取非负值，即非负最小二乘解k.

‖L(λ)-S(i)k*‖2=min‖L(λ)-S(i)k‖2(k∈Rt).

(5)

在仿真试验中，为了比较拟合光谱与目标光谱的匹配程度,引入相关指数R2作为评价参数[9],计算如(6)式：

(6)

式(6)中yi表示目标光谱数据.对于光谱匹配而言，R2越接近于1,拟合光谱与目标光谱的相似程度越高，匹配的结果越好.

1.2 光谱数据库

为了满足实际应用的需求，通过对市场中LED光源进行调研，最终选用15种常用LED光源即2种白光LED和13种单色LED进行光谱测试，并将光谱信息汇总导入到程序中，建立LED光谱数据库,其光谱能量分布如图1所示.对于单色LED，其光谱数学模型可以用改进后的高斯分布函数表示，仅用多个单色LED混光后合成的白光显色性较差，应用范围受到了一定的限制；光谱曲线在波峰位置处较为尖锐，很难实现与平滑光谱曲线的匹配.本次研究中选用两种白光LED作为芯片库光谱数据，在很大程度上丰富了光谱数据库，提高了对平滑光谱曲线匹配时的相似程度.

2 仿真试验

发光二极管作为一种冷光源,光电转换效率只有50%左右，其余能量则会以发热的形式损耗，因此散热一直是LED产业面临的重大难题之一[10].而解决该问题最简单有效的方法之一，便是减少光源封装使用的LED个数.

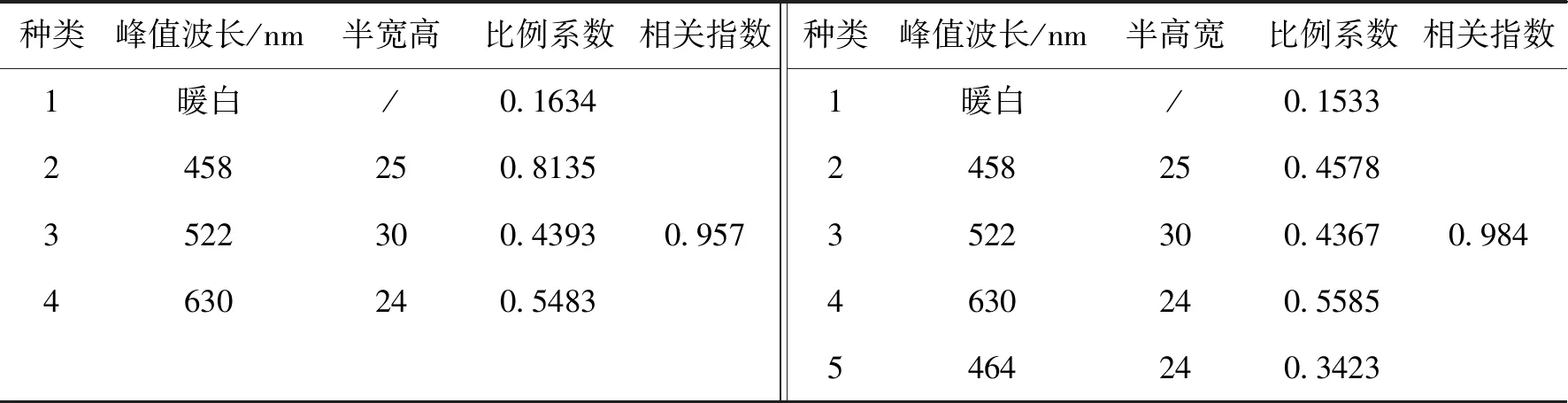
基于上述光谱匹配的原理，选用实验室中用于健康照明的其中一个光谱作为目标光谱.为了求出拟合光谱与目标光谱相似程度最高时对应的LED个数，根据光谱匹配选用的LED个数，使用Matlab编程软件实现对库中光谱数据的列举，通过匹配计算找出最佳的LED组合.图2为从数据库中分别选用4种、5种、6种和7种LED进行匹配的最佳结果，表1和表2分别列出了所选用LED种类及比例系数.

图1 数据库中LED光源的光谱辐射强度分布Fig.1 The spectral radiation intensity distribution of LED light source

种类峰值波长/nm半宽高比例系数相关指数种类峰值波长/nm半高宽比例系数相关指数1暖白/0.16342458250.81353522300.43934630240.54830.9571暖白/0.15332458250.45783522300.43674630240.55855464240.34230.984

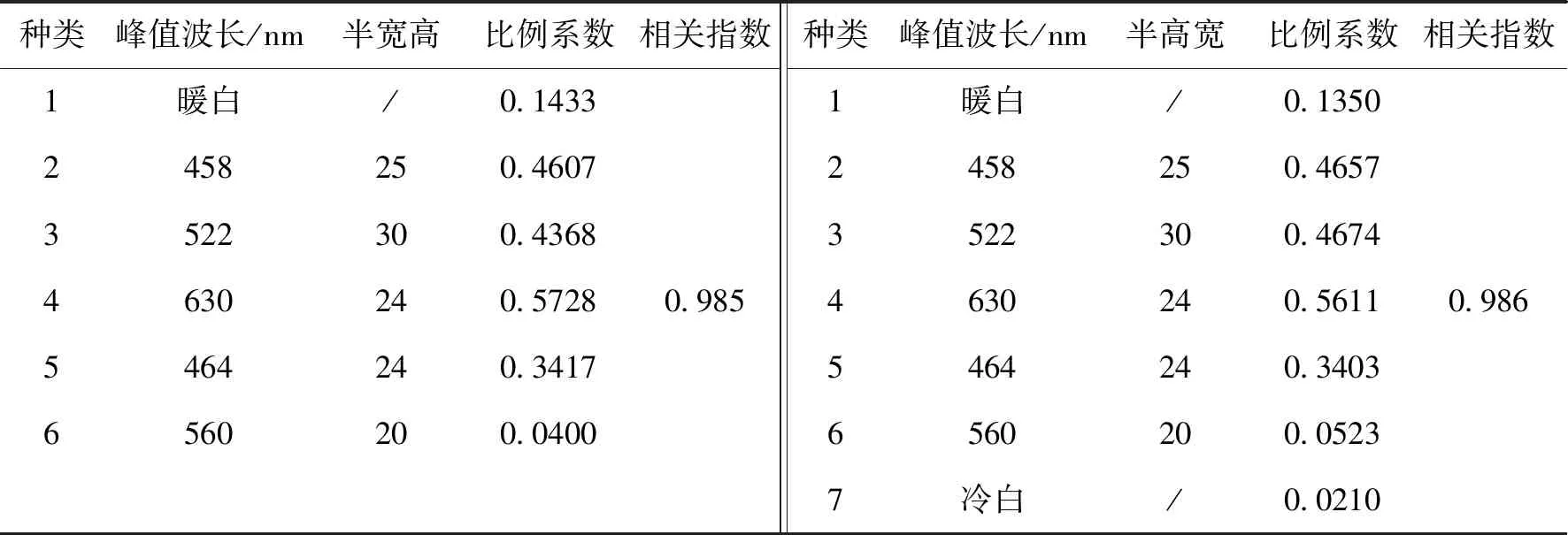
表2 选用6种、7种LED进行匹配的最佳组合及参数

图2(a)是从数据库中随机选4种LED进行匹配的最佳结果，由于匹配选用的LED种类较少，拟合后的光谱缺少峰值波长为460 nm的单色LED，相关指数为0.957(表1)，拟合光谱与目标光谱的相似程度较差；图2(b)为选用峰值波长458,464,522,630 nm单色与暖白5种LED对目标光谱进行匹配，相比于图2(a)的4种LED，光谱更加丰富，能够实现对蓝光的补光，提高了与目标光谱的相似程度，相关指数可以达到0.984(表1).

由表2可知，继续增加匹配选用的LED个数时，相关指数变化很小，增加的单色LED比例系数仅为0.0400,0.0210.这也就表明，新增的两种光源对目标光谱的匹配作用很小，只是补充了很小一部分的光谱曲线.虽然新增的LED光源可以稍微提高匹配的精度，但是考虑到封装及散热等问题，数量较多的LED光源对封装结构有很高的要求，出光品质也会受到一定的影响.综合以上分析，精度略微提高不能弥补LED光源增加对实际应用带来的影响，因此，最少选用5种LED光源可以实现对目标光谱的匹配.

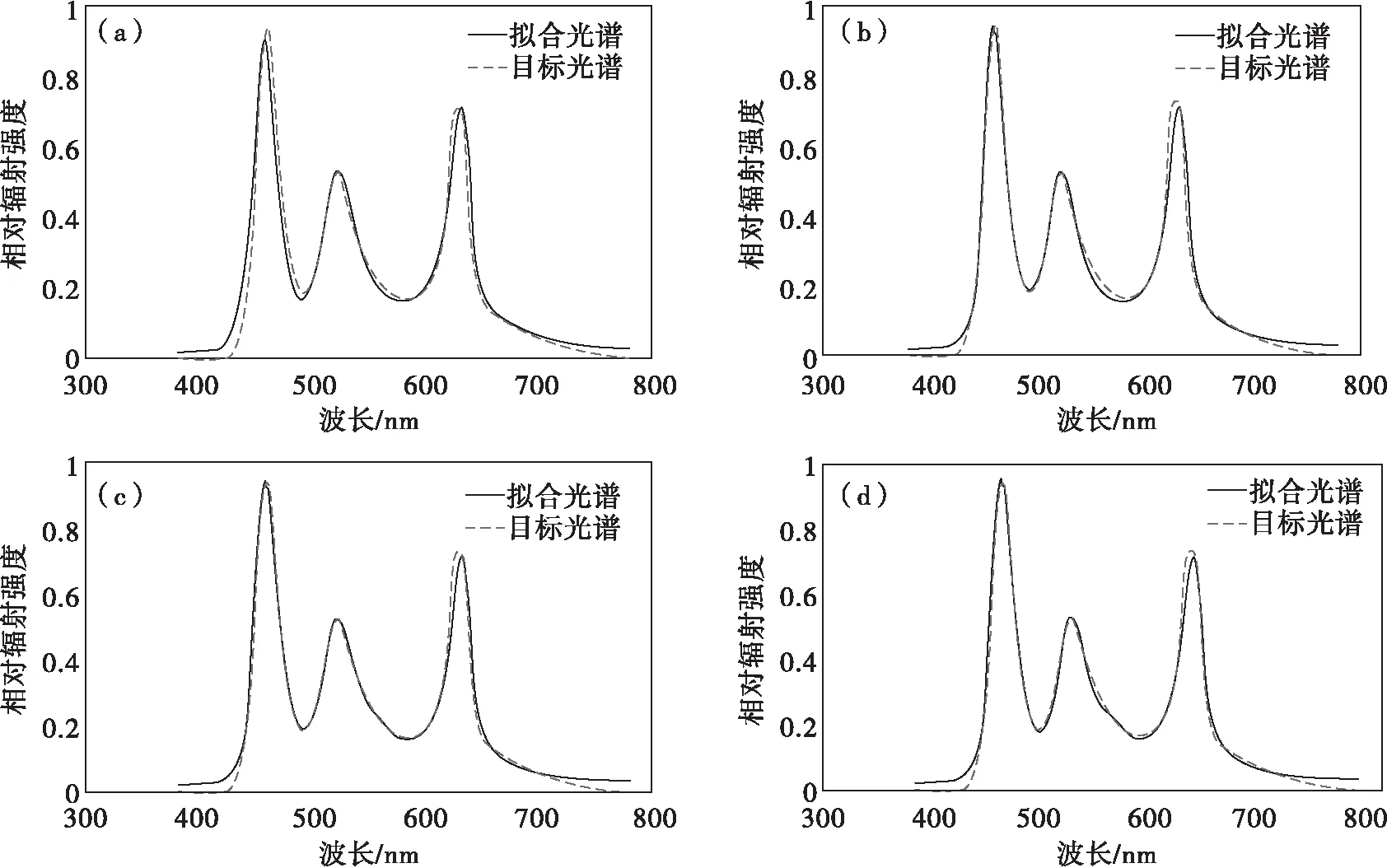
图2 不同种类LED进行匹配的最佳结果(a) 4种；(b) 5种；(c)6种；(d) 7种Fig.2 Different kinds of LED to match the best results(a) four;(b)five;(c)six;(d)seven

3 结 论

从工程实际应用角度出发,选用15种LED进行光谱测试并建立光谱数据库.利用光谱叠加原理，使用数据库对健康照明实验室中其中一个光谱进行匹配，在分别选用4～7种LED光源时，其对应的相关指数均达到0.95以上，能较好实现与目标光谱的匹配，并且选用的LED种类越多，相关指数越大，匹配越精确.当增加的LED个数超过5种时，每增加一种LED光源，相关指数仅增加0.001.基于散热问题的考虑，可以使用5种LED光源实现对目标光谱的匹配.