周期为2q理想几乎四进制序列构造研究
彭秀平,冀惠璞,郑德亮,牛晓霞
(1.燕山大学信息科学与工程学院,河北 秦皇岛 066004;2.河北省信息传输与信号处理重点实验室,河北 秦皇岛 066004)
1 引言
四进制序列由于具有恒定的包络特性和系统易于实现等特性,被广泛应用于雷达、声纳、导航、码分多址(CDMA,code division multiple access)等实际通信系统中。在实际应用中,为了实现同步、抗多径干扰和防止载波泄露等需求,通常要求所采用的序列具有尽可能低的自相关函数旁瓣值和好的平衡性。自相关函数旁瓣值全为0的序列称为最佳序列,而最佳二进制序列仅存在长度为4的(1,1,1,−1)情况,最佳四进制序列仅存在长度为2、4、8和16的情况,且平衡的最佳四进制序列根本不存在[1]。为此,对理想四进制序列和理想几乎四进制序列的研究受到了国内外学者的广泛关注,对于奇数长的理想四进制序列,Schotten等[2-3]构造了周期为(其中p为奇素数,a为正整数)的一类旁瓣值全为1的理想四进制序列。随后,Lüke等[4]利用改进的Legendre序列构造了理想奇周期四进制序列。对于偶数长的理想四进制序列,Tang等[5]证明了周期为偶数长的平衡四进制序列的自相关函数旁瓣值最大模值至少为2的特性,并明确了此周期长平衡四进制序列的理想情况为自相关函数旁瓣模值为小于等于2的情况。逆Gray映射将二进制序列同四进制序列建立了联系,随后这种方法被广泛应用于构造具有理想自相关特性的平衡或几乎平衡的四进制序列,主要包括采用Sidelnikov[6]序列、理想自相关二进制序列[7]、Legendre序列[8]等。此外,分圆类方法也被广泛用于四进制序列的构造中,Edemskiy等[9]运用四阶分圆与中国剩余定理结合的方法分别得到了2种旁瓣值为{-4,2,-2,0}和{-2±2i,±2i,-2}且周期为N=2q(q为奇素数)的平衡四进制序列,但是其旁瓣值的最大模值分别为4和8,不符合平衡理想四进制序列的标准,在此基础上,Shen等[10]基于广义分圆类思想,提出了2种新的可以得到周期为N=2q(q为奇素数),旁瓣值为{2,-2}的理想四进制序列的构造方法,但是此方法将四进制序列0位置和q位置的元素值固定为1和–1,属于四进制序列元素的特殊情况。
为了进一步扩大理想四进制序列的存在范围,近些年,通过在序列中引入适当个0元素的方式,有关理想几乎四进制序列的构造方法被相继提出。代表性成果有Tang等[11]通过引入一个0元素的方式,基于四阶分圆的方法构造得到一种周期为素数且N≡1(mod4),旁瓣值为-1的理想几乎四进制序列。彭秀平等[12]中通过引入4个0元素基于交织法对周期为N≡0(mod4)且旁瓣值为{0,-4}的几乎四进制序列的构造方法进行了研究。本文通过在四进制序列中引入一个或2个0元素的方式,基于中国剩余定理和四阶分圆类对周期为N=2q(q为奇素数)的理想几乎四进制序列的构造方法进行研究,根据几乎四进制序列y的y(0)和y(q)这2个位置中含0个数不同提出相应构造方法,当(y(0),y(q))=(0,0)时,得到2种旁瓣值为{0,-2}和{0,2,-2}的平衡理想几乎四进制序列,当y(0)和y(q)中有一个位置为0时,得到2种旁瓣值为{0,2,-2}和{0,-2,-2i,2i} 的平衡理想几乎四进制序列。
2 基本概念
定义1[13]设周期为N的序列y=(y(0),y(1),⋅⋅⋅,y(N-1)),其中y(t)∈{1,-1,i,-i},i=-1,则称序列y为四进制序列,其自相关函数定义如式(1)所示。
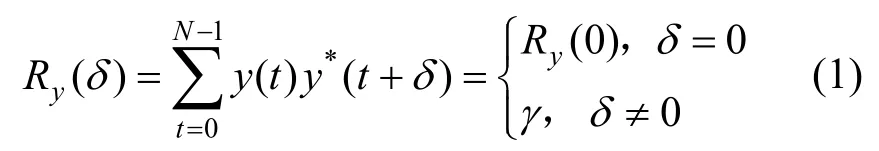
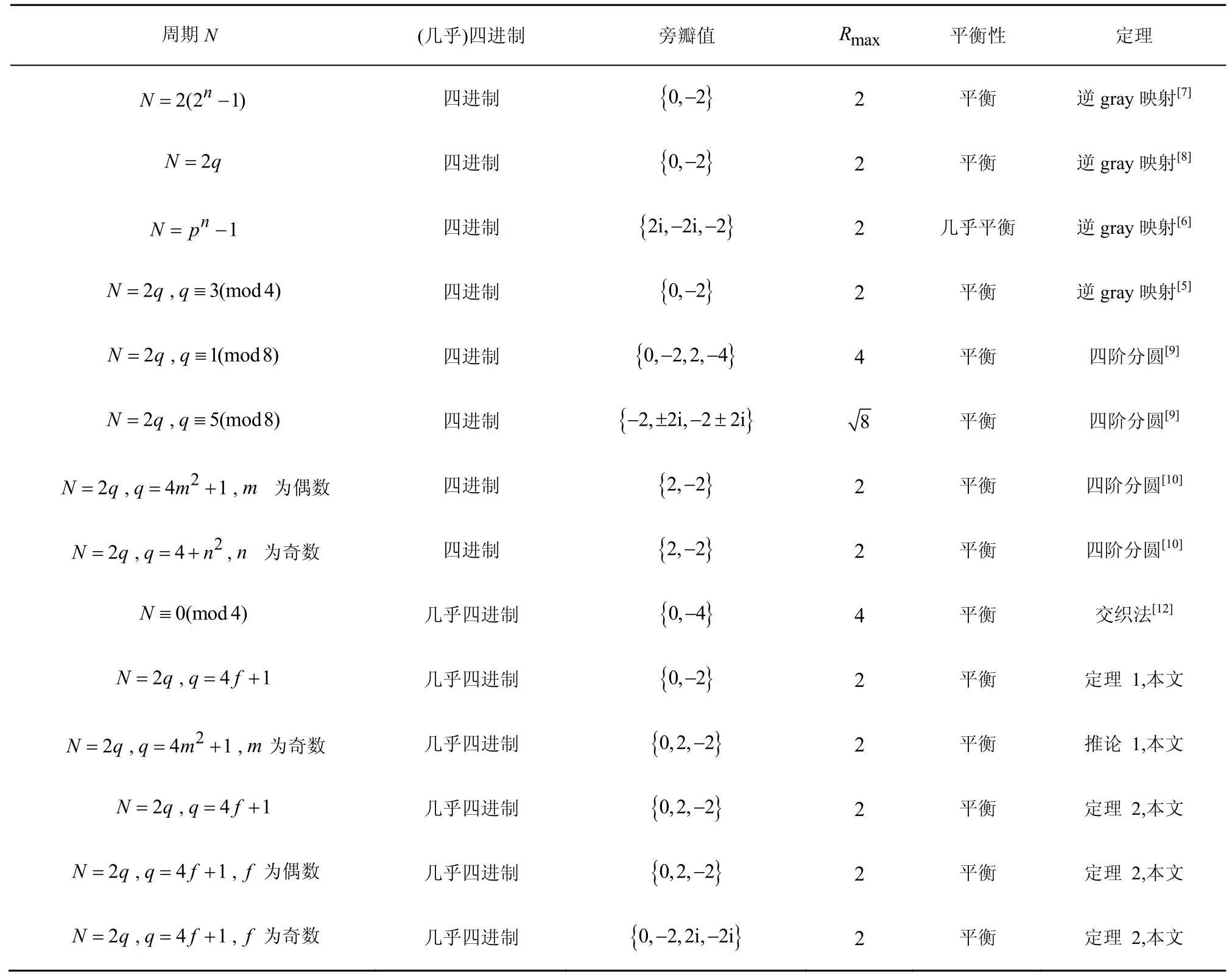
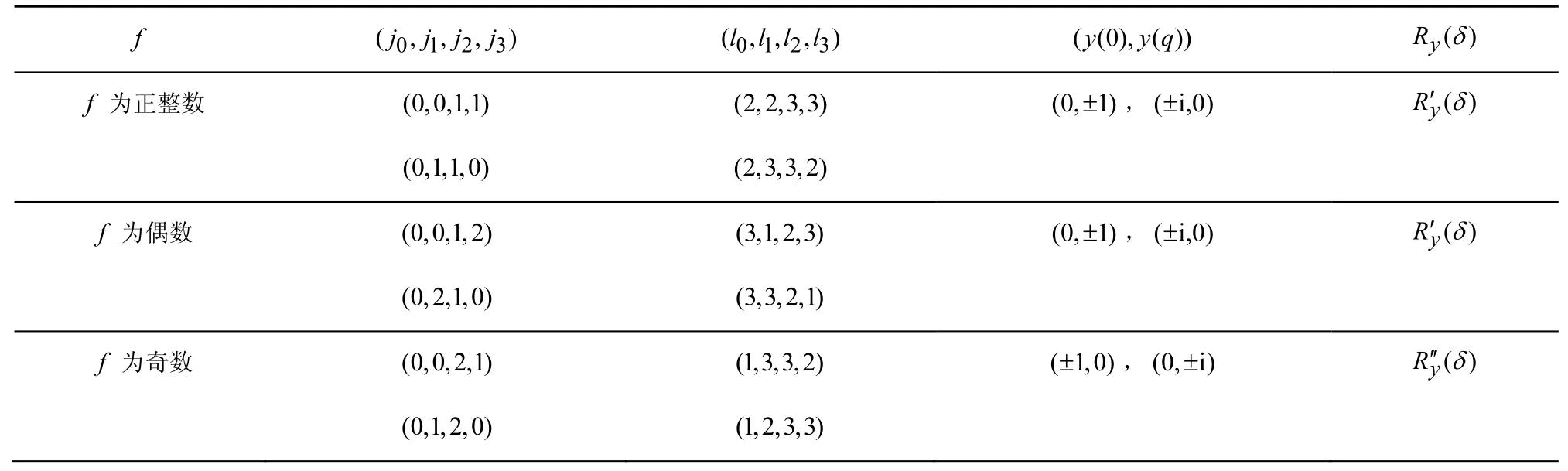
其中,0≤δ 引理1[5]设表示序列y的自相关函数的最大旁瓣模值,那么对于周期为N≡0(mod2)>2的平衡四进制序列,一定满足Rmax≥2。因此,若周期为N≡0(mod2)>2的平衡四进制序列y的自相关函数满足Rmax=2,则称序列y为平衡理想四进制序列。 本文基于此理论界,通过在四进制序列的基础上引入一个或2个0元素的方式,提出了几种满足此理论界,周期为N=2q的平衡理想几乎四进制序列的构造方法。 定义2[13]设q=4f+1为奇素数,θ是有限域GF(q)上的本原元,令 则称Hi为GF(q)上的四阶分圆类。令 其中,Hi+1代表集合{hi+1,hi∈Hi},“+”代表和模q,则(i,j)称作基于GF(q)的四阶分圆数。 引理2[13]设q=4f+1为奇素数,其中f为正整数。q又可表示为q=4m2+n2,其中m、n均为正整数。根据f的奇偶性和n≡1(mod4)或n≡3(mod4)不同取值将四阶分圆数进行如下分类。 当f为奇数时,Zq上的四阶分圆数的关系如式(4)所示,Zq上的四阶分圆类的5个基本分圆数如表1所示。 表1 当f为奇数时,Zq的四阶分圆数的5个基本分圆数 当f为偶数时,Zq上的四阶分圆数的关系如式(5)所示,Zq上的四阶分圆类的5个基本分圆数如表2所示。 表2 当f为偶数时,Zq上的四阶分圆数的5个基本分圆数 引理3[14]根据中国剩余定理,Z2q≅Z2×Zq存在如式(6)所示映射关系。 定义3周期为2q的几乎四进制序列y(t)定义如式(7)所示。 其中,y(0),y(q)∈{0,1,-1,i,-i},并且y(0),y(q)中至少有一个为0。 定义4设周期为N的几乎四进制序列y的元素集为Y={0,1,-1,i,-i},Y*=Y/{0},令当满足式(8)所示条件时,几乎四进制序列y称为平衡序列。 定义5[10]设A和B是整数环Z2q上的2个子集,差函数dδ(A,B)定义为 其中,B+δ代表集合{b+δ:b∈B},“+”代表和模2q。 定理1设q=4f+1=4m2+n2为一奇素数,其中f为正整数,令(y(0),y(q))=(0,0),由式(7)定义的序列y(t)中各参数满足表3所示集合时,构造得到的几乎四进制序列均是理想平衡几乎四进制序列,且其相关函数值如式(11)所示。 表3 满足定理1的序列y(t)的参数集合 证明以(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,1,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(2,2,3,3)为例进行证明,根据定义3可以得到 因为(y(0),y(q))=(0,0),所以由定义4可知,该构造方法所得的几乎四进制序列y是平衡的。 令序列y的自相关函数Ry(δ)=Re(Ry(δ))+iIm(Ry(δ)),其中Re(Ry(δ))表示Ry(δ)的实部,Im(Ry(δ))表示Ry(δ)的虚部。由定义5、引理4和引理5可以计算得到式(13)和式(14)。 1)当δ0=0,δ1=0时,显然,Ry(0)=2q-2。 2)当δ0=0,δ1≠0时,令δ1∈Hh,h∈{0,1,2,3},由引理2和引理6可知, a)若f为奇数,则Ry(δ)=2[3(0,0)+(0,2)-(0,1)-(0,3)-2(1,0)](16) 当n≡1(mod4)时,Ry(δ)=-2。 当n≡3(mod4)时,Ry(δ)=-2。 b)若f为偶数,则 Ry(δ)=2[3(0,2)+(0,0)-(0,1)-(0,3)-2(1,2)](17) 退役复学高职生有的在陆军服役,有的在海军服役,有的在空军、武警等部队服役;有的虽然属于同一兵种,但服役岗位不同;有的是普通战士,有的是特种兵。兵种和身份的不同,决定了他们在部队的生活经历有很大差异。从调研结果看,特种兵比其他兵种更具有责任心和积极进取的精神,更乐于无私奉献;在部队担任过领导职务或立过军功的战士,大多数都是党员,复学后更容易成为班级的骨干或核心人物。 当n≡1(mod4)时,Ry(δ)=-2。 当n≡3(mod4)时,Ry(δ)=-2。 所以,Ry(δ)=-2。 3)当δ0=1时,由于{0}∩{1}=0,因此 Ry(δ)=Re(Ry(δ))=0。 综上所述,其相关函数值如式(11)所示,由此可知得到的几乎四进制序列为理想平衡几乎四进制序列。其他组合情况证明过程与上述证明过程类似,不再赘述。证毕。 例1设q=17=4×4+1=4×22+1,取θ=2,可以得到 根据定理1可以得到 且其相关函数值为 推论1当q=4f+1=4m2+n2为一奇素数,m为奇数,n=1,且(y(0),y(q))=(0,0)时,由式(7)定义的序列y(t)满足表4所示集合时,构造得到的几乎四进制序列是理想平衡几乎四进制序列,且其相关函数值如式(18)所示。 表4 满足推论1的序列y(t)的参数集合 证明推论1的证明与定理1的证明类似,在此省略。 例2设q=5=4×1+1=4×12+1,取θ=2,可以得到 当(a0,a1,a2,a3,)=(0,0,0,0),(j0,j1,j2,j3,)=(0,1,2,3),(b0,b1,b2,b3,)=(1,1,1,1),(l0,l1,l2,l3,)=(0,3,2,1)时,根据推论1,可以得到 且其相关函数值为 因此,序列y是平衡的理想几乎四进制序列。 推论1是对定理1方法的补充,即当q=4f+1=4m2+n2,其中m为奇数,n=1的情况,这些特殊长度除了满足定理1的构造方法外,还满足推论1的构造方法。 定理1与推论1是在四进制序列中引入了2个0元素,即(y(0),y(q))=(0,0),接下来的定理2中通过引入一个0元素,即y(0)和y(q)其中有一个为0,同样,可以得到自相关函数旁瓣值的最大模值为2的平衡理想几乎四进制序列。 定理2设q=4f+1=4m2+n2为一奇素数,其中,f、m、n都是正整数,当(y(0),y(q))的取值只有一个为0时,由式(7)定义的序列y(t)满足(a0,a1,a2,a3)=(0,1,0,1),(b0,b1,b2,b3)=(0,1,0,1)和表5所示集合时,构造得到的几乎四进制序列是平衡理想几乎四进制序列,且其相关函数值如表5所示。和分别为 证明定理2的证明与定理1的证明类似,取(y(0),y(q))=(0,1),(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,1,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(2,2,3,3),根据定义3可得 由引理4和引理5可得 表5 满足定理2的序列y(t)的参数集合 例3q=17=4×4+1=4×22+1,取θ=2,其分圆类和分圆数与例1相同,此时,若(y(0),y(q))=(0,1),(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,1,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(2,2,3,3),根据定理2可以得到 且其自相关函数值为 例4设q=5=4×1+1=4×12+12,取θ=2,其分圆类和分圆数与例2相同,此时,若(y(0),y(q))=(0,i),(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,2,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(1,3,3,2),根据定理2可以得到 且其自相关函数值为 通过在四进制序列中引入一个或2个0元素的思想,基于四阶分圆类和中国剩余定理,本文得到了许多新的周期长度为2q(q为奇素数)的平衡理想几乎四进制序列。表6列出了目前已有的偶数长理想四进制序列同本文得到的理想几乎四进制序列在构造方法和性能特性方面的对比结果。由表6可知,本文得到的所有几乎四进制序列的Rmax=2,满足文献[5]中给出的理论界要求,且都具有很好的平衡性。与文献[5-8]相比,文献[5-8]得到的理想四进制序列都是由特殊的二进制序列进行逆gray映射得到的,且文献[9]得到的四进制序列是几乎平衡的。而本文提出的构造方法是一种直接构造,性能特性不受所采用的二进制序列特性限制,都是平衡的;与文献[9-10]相比,虽采用的都是分圆类方法,但是文献[9]得到的四进制序列的,不满足理想四进制序列的理论界,文献[10]的序列虽然满足理想四进制序列的理论界,但是存在空间相当有限,在q≤100内仅存在q=5,13,17,29,53这5种情况,而通过本文方法可将q的范围扩展到q=5,13,17,29,37,41,53,61,73,89,97。所以通过本文构造方法,可以得到更多平衡的理想四进制序列,为实际工程应用和通信系统提供了更多的可供选择的信号范围。 表6 现有的偶数长(几乎)四进制序列的比较
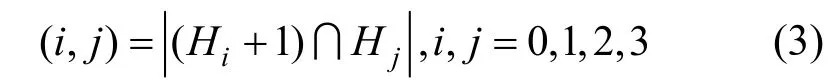
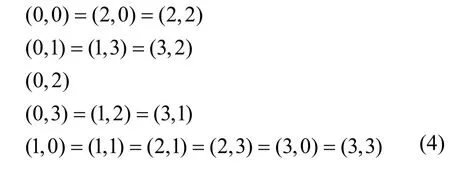



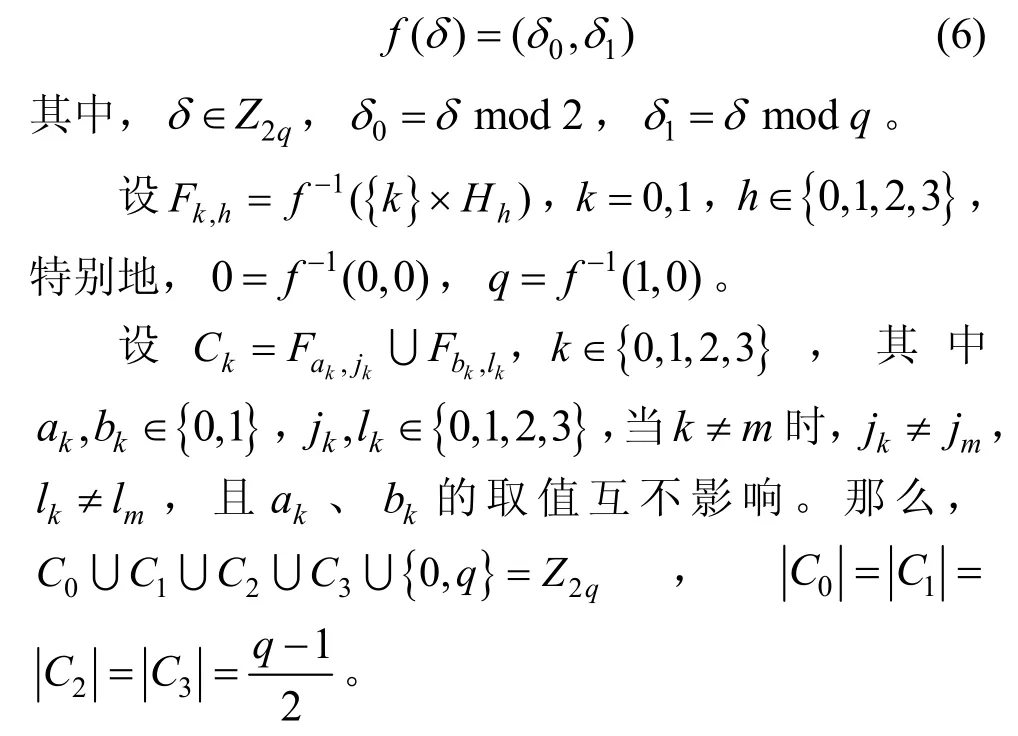
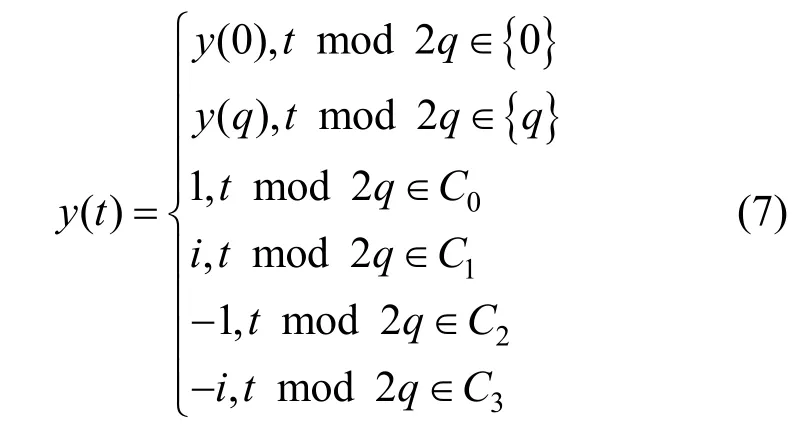
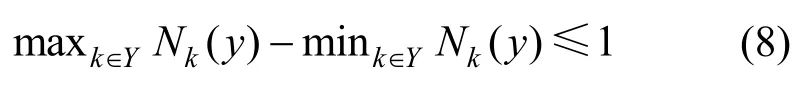
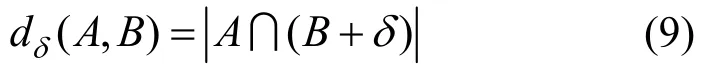

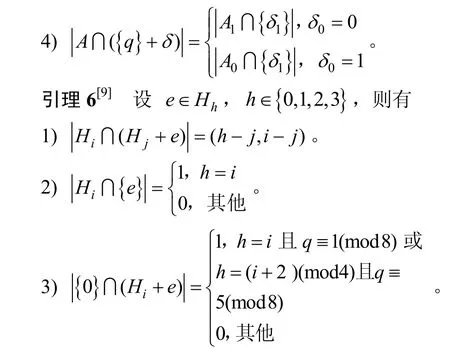
3 理想几乎四进制序列构造
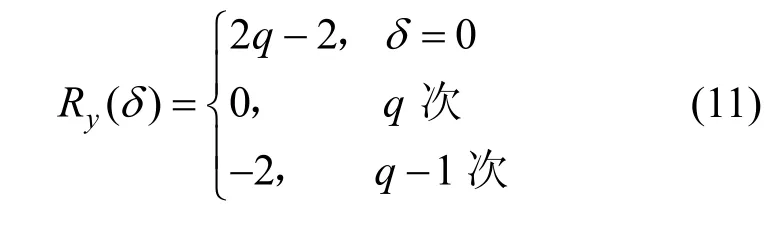

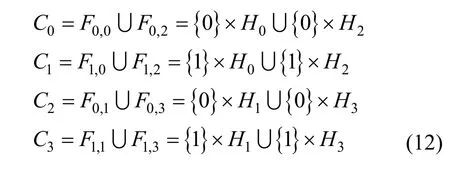
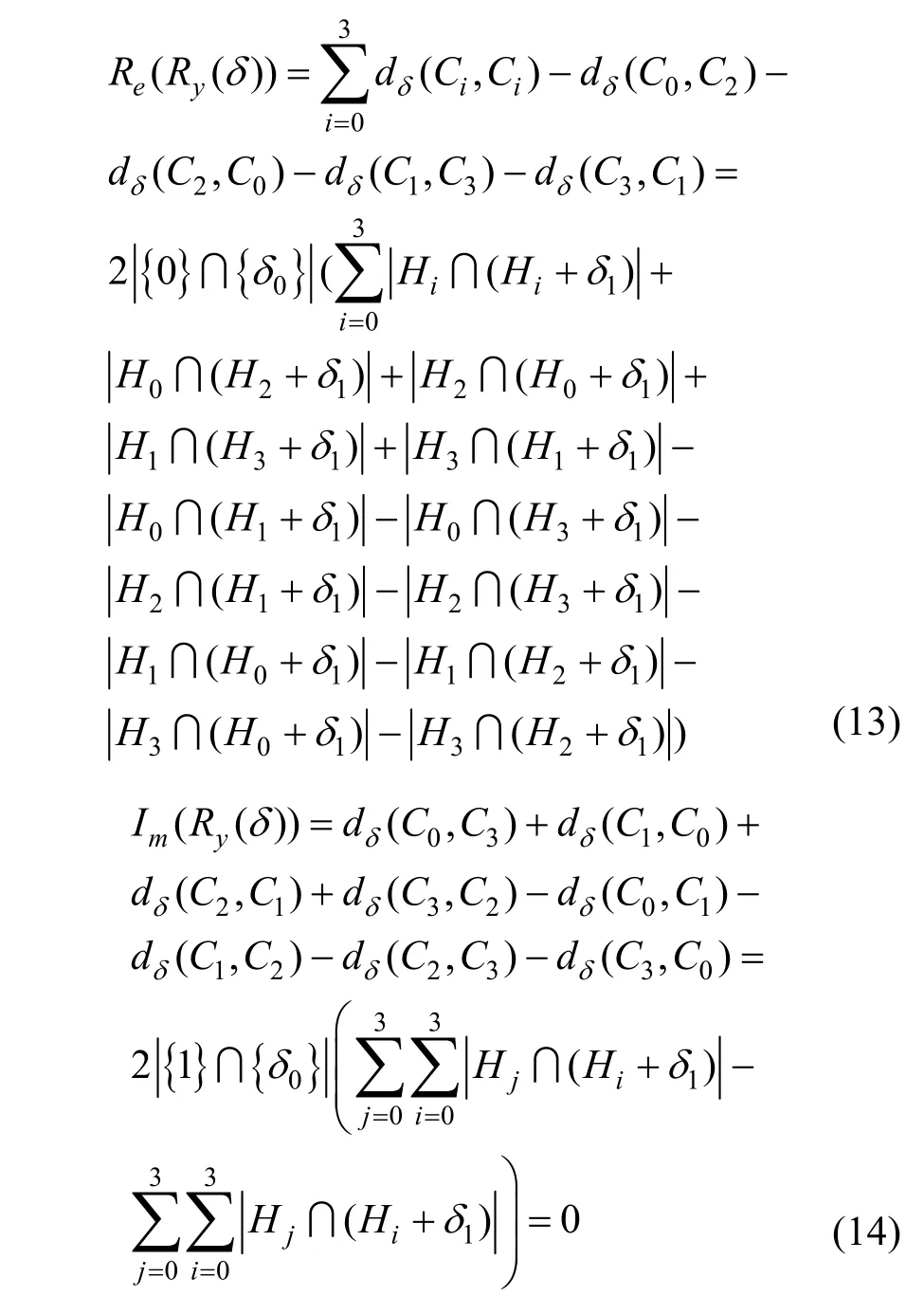
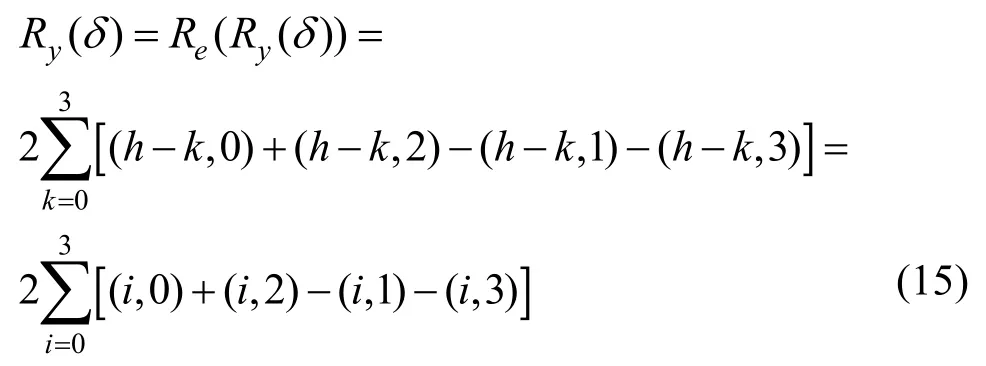


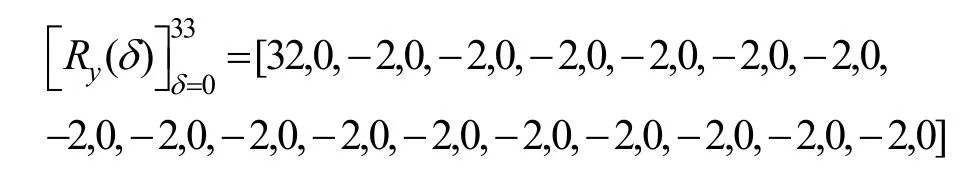
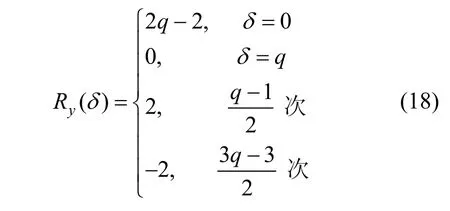


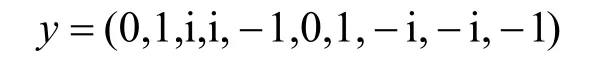
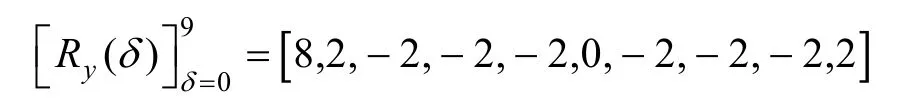
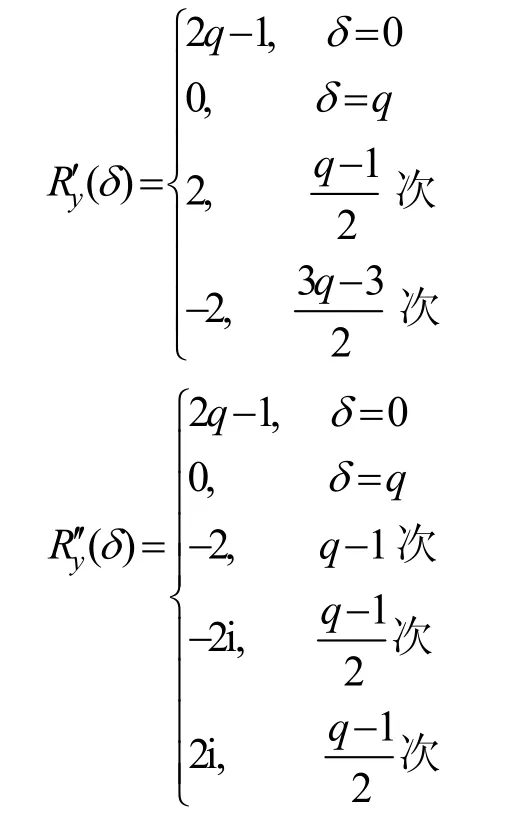





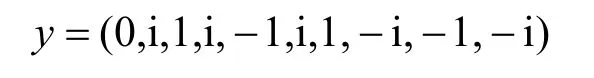
4 结束语