基于压缩感知的FBMC/OQAM系统信道估计方法

袁伟娜，严秋

（华东理工大学信息科学与工程学院，上海 200237）

1 引言

近年来，在无线通信系统中，滤波器组多载波（FBMC,filter bank multi-carrier）技术成为正交频分复用（OFDM,orthogonal frequency division multiplexing）技术的替代方案之一，引起了许多研究者的关注[1]。作为下一代无线通信网络的潜在候选多载波调制方案[2-3]，FBMC常与偏移正交幅度调制（OQAM,offset quadrature amplitude modulation）技术结合，充分利用时频局部化特性，并采用基于滤波器组的脉冲整形，提供了与无循环前缀（CP,cyclic prefix）的OFDM系统相似的频谱效率；由于其放宽了正交条件，因此具有良好的抗干扰能力[4]。虽然FBMC具有良好的频谱利用率、抗带外泄露和抗干扰的特性，然而，子载波基函数只在实数域上是正交的，因此，相邻子载波和符号之间总是存在固有的虚部干扰。

固有的载波间/符号间干扰将使FBMC信道估计变得更加复杂。因此，现有的OFDM信道估计方法不能直接应用于FBMC/OQAM系统。近年来，国内外研究了多种导频方案和相关的估计方法。2种经典的基于导频的方法是干扰近似法（IAM,interference approximation method）[5-6]和干扰消除法（ICM,interference cancellation method）[7-8]，它们的本质是消除固有干扰或者利用它来提高估计性能。然而，由于难以完全消除虚部干扰，因此基于导频的信道估计方法的性能不是特别理想。

为了提高FBMC信道估计的性能，研究者们已经做了很多工作。文献[9]提出了一种辅助导频信道估计方法。相对于IAM和ICM，辅助导频方法（APM,auxiliary preamble method）在估计频域信道响应的同时，只需要2个与CP-OFDM系统相同的实值符号持续时间，而不会损失估计性能的准确性。文献[10]研究了一种编码辅助导频信道估计方法，该方法利用编码辅助导频符号来消除对每个散射导频的假想干扰。文献[11-12]还研究了半盲和盲符号定时估计方法。然而，这些方法具有较高的计算复杂度，可能出现相位模糊，并需要较长的测量数据，这在一定程度上限制了其可用性。在实践中，无线信道往往呈现稀疏多径的结构特性，可建模为时间–频率双选信道[13-14]，其响应在时延–多普勒域呈现稀疏性，使压缩感知（CS,compressive sensing）技术[15-17]得以应用到稀疏信道估计中。在过去的几年里，人们已经研究了基于CS的OFDM系统信道估计[18-19]。然而，对于基于CS的FBMC/OQAM系统信道估计的研究很少。文献[20]提出了一种改进的IAM，并利用正交匹配追踪（OMP,orthogonal matching pursuit）算法重建信道脉冲响应。结果表明，与传统的基于导频的最小二乘（LS,least square）方法相比，基于OMP[21]的方法可以获得显著的性能改善。文献[22]研究了FBMC/OQAM系统下基于IAM和ICM的信道估计方法。新的自适应压缩采样匹配追踪（ARCoSaMP,adaptive regularized compressive sampling matching pursuit）算法结合了稀疏度自适应匹配追踪（SAMP,sparsity adaptive matching pursuit）算法和压缩采样匹配追踪（CoSaMP,compressive sampling matching pursuit）算法的特点，其估计性能优于基于传统贪婪重构算法的信道估计方法。

针对FBMC/OQAM系统，在辅助导频和编码方法的基础上，本文提出了一种新的稀疏信道估计方法——基于Tanimoto系数的弱选择正则化正交匹配追踪（T-SWROMP,Tanimoto based stagewise weak and regularized OMP）算法。该算法的优点是不需要已知信道的稀疏信息，基于Tanimoto系数度量准则，然后利用弱选择标准，结合正则化的思想，优化支撑集的选择，迭代地改进了原信号的近似值，信号重构效果得到提升。仿真结果表明，新方法比传统的OMP、分段弱正交匹配追踪（SWOMP,stagewise weak OMP）和正则化正交匹配追踪（ROMP,regularized OMP）方法具有更好的误比特率（BER,bit error ratio）性能。

本文中，ℜ{⋅}表示取实部，diag{⋅}表示对角矩阵，ℝ和C分别表示实数域和复数域，(⋅)-1表示一般逆运算，(⋅)#表示矩阵的逆，(⋅)T和(⋅)H分别表示转置和共轭转置，IM表示M维的单位矩阵。

2 FBMC系统稀疏信道模型

在FBMC/OQAM系统中，发送的信号可以表示为[5]

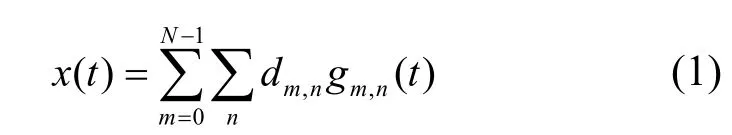
其中，dm,n表示实值OQAM符号；gm,n(t)表示合成基，可以是由原型函数gm,n(t)通过以下方式获得

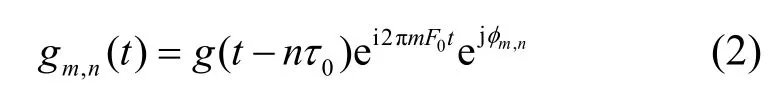
其中，F0表示系统的子载波间隔，τ0表示FBMC 系统的符号间隔。在OFDM系统中，，但是在FBMC系统中，，所以有。且脉冲g的设计使相关子载波函数gm,n(t)在实数域正交

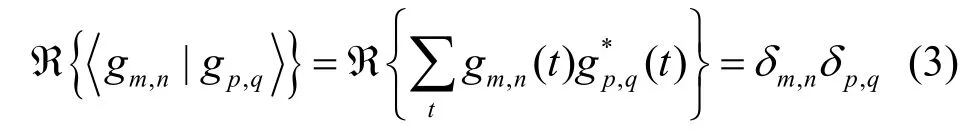
其中，δi,j代表克罗内克函数，如果m≠p，那么δm,p=0；如果m=p，那么δm,p=1。可以发现，即使在无失真的信道中，在时间和频率完全同步的情况下，输出端仍然存在载波间虚部干扰，因此定义干扰权重为

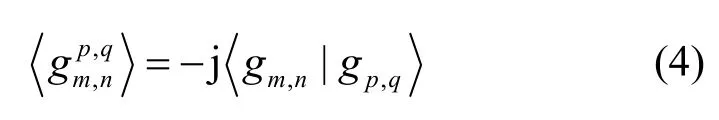
通过带有加性噪声的信道，接收到的信号可以表示为

另外，有

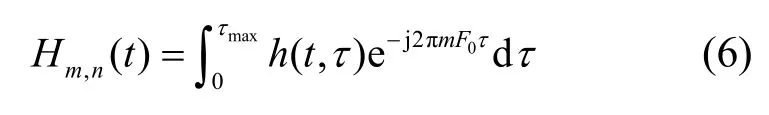
其中，h(t,τ)表示信道脉冲响应，Hm,n(t)表示时刻t信道的复数响应。

式(5)中的信号r(t)的矩阵形式可以表示为

其中，X=diag{x(0),x(1),…,x(N-1)}；R=diag{r(0),r(1),…,r(N-1)}T；H=FNLh表示多径信道频率响应采样值，FNL表示N×L维离散傅里叶变换矩阵，L是信道长度；Φ表示N×N大小的噪声矩阵，均值为0，方差为σ2。

假设导频数量为P，ϕ=(es1,es2,…,esP)表示大小为P×N的导频选择矩阵，ϕ用于从整个子载波中寻找导频位置，si(i=1,2,…,P)表示第i个导频的位置。式(7)可写为

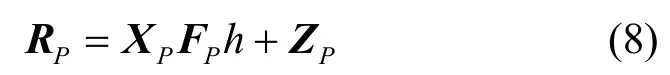
其中，RP=φR是收到的导频信号，在本文中，RP是LS信道估计值，ΦP=ϕφ，FP=φFNL，XP=φXφT是对角线矩阵，其中对角线元素是导频值。

假设F=XPFP，重写式(8)为

其中，h表示稀疏多径信道响应，在传输过程中可以得到RP和F。然后，本文可以用CS重构算法来恢复稀疏信号h。

3 基于T-SWROMP算法的稀疏信道估计

在基于导频符号辅助的信道估计中，导频符号在接收端是先验的。在OFDM中，由于干扰权重是一个单位矩阵，导频位置上接收到的符号除以相应的数据符号，即可得到导频位置上信道系数的估计值，然后通过插值来获得数据位置处的信道值。然而，在FBMC中，这种简单的方法由于虚部干扰而不起作用，即由非对角虚元素组成。

牺牲一个额外的数据符号，即所谓的辅助导频符号，可以消除一个导频位置上的虚部干扰。图1显示了本文的辅助导频结构。其中■表示数据，表示辅助导频。如果选择辅助导频符号，可以完全消除导频位置处的虚部干扰，所以有

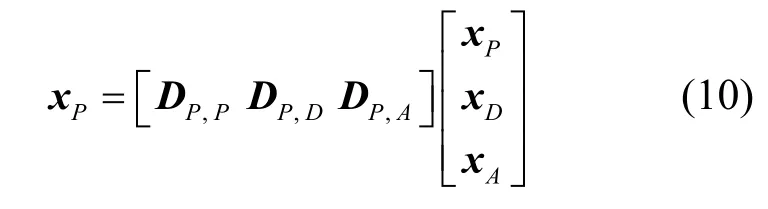
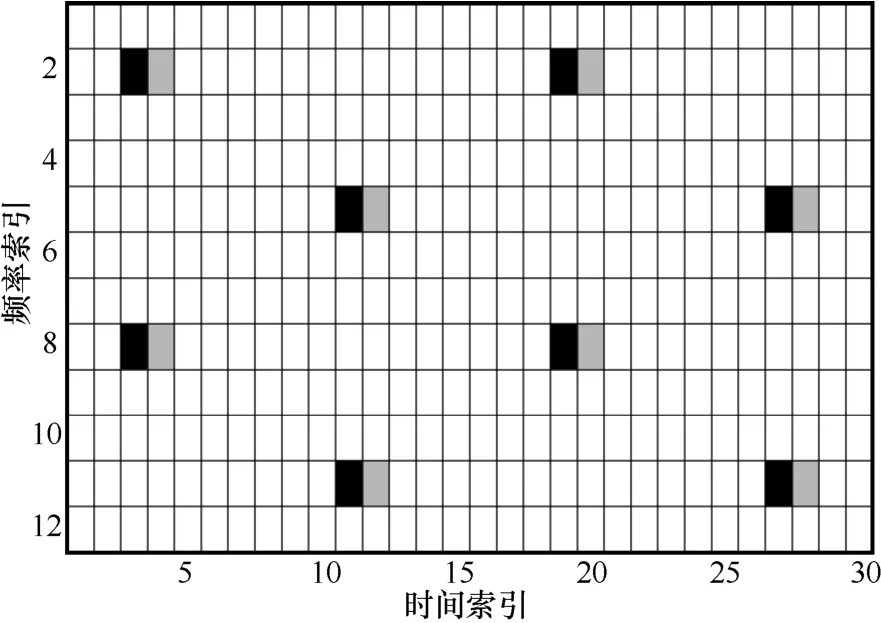
图1 辅助导频放置方式

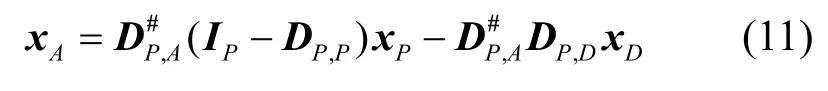
其中，有

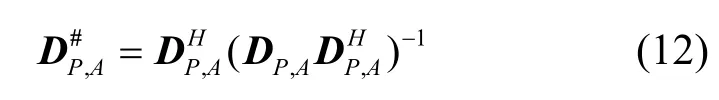
如果导频符号彼此间隔足够远，则DP,P将成为一个单位矩阵，从而可以简化式(11)。

编码方法是指不使用辅助符号，将数据进行编码从而消除导频处的虚部干扰的方法。图2显示了本文的编码辅助导频结构。因此，将发送的信号改写为

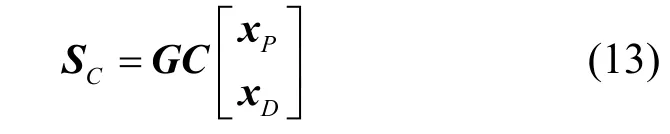
经过信道估计后，本文用CT对均衡后接收的信号进行解码，而条件必须保持不变，即编码向量ci是正交的，因此传输系统与不编码的情况相似。假设导频符号之间的间隔足够远，允许为不同的导频符号独立设计编码。因此，找到C的问题可以简化为找到一个更小的编码矩阵，通过该矩阵编码得到最接近导频的N个干扰符号，从而消除干扰。

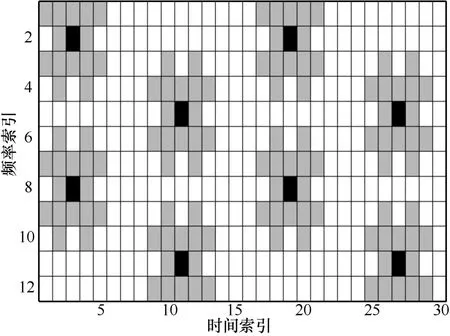
图2 编码辅助导频放置方式

要很好地进行稀疏信道估计，除了合适的导频结构外，还需要较优的CS重构算法。

OMP、ROMP和SWOMP算法[24]是基于迭代贪婪追踪的CS重构算法。对于OMP算法，在每次迭代中，只选择与残差内积绝对值最大的一列。ROMP算法则是先选出内积绝对值最大的K列，然后从这K列中按正则化标准再筛选一次，其在信号重构过程中，每次迭代都是根据残差r与测量矩阵Φ中原子相似度，挑选与信号稀疏度相同的K个原子索引集作为候选集J，所以稀疏度K直接影响信号的重构精度。因此，为解决ROMP算法在信号重构中需已知信号稀疏度K的问题，结合SWOMP算法中原子的弱选择标准，即

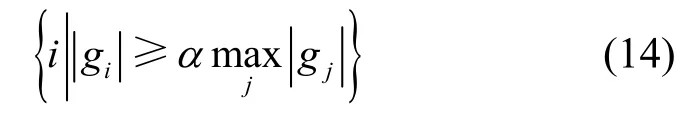
其中，i∈J，α∈(0,1]。

将残差r与测量矩阵Φ中原子的相似度即内积值g满足式(14)的所有原子对应的索引集i并入候选集J中，则完成了一次原子的弱选择。ROMP算法结合弱选择标准使原算法在信号重构过程中不再依赖稀疏度，并且根据残差r与测量矩阵Φ中各原子相似度的不同，自适应地调节原信号的原子个数，更好地挑选出表示原信号的原子候选集，进而提升信号重构精度及稳定性。

同时，在信号重构过程中，弱选择正则化正交匹配追踪算法[15]采用了Cosine相似度度量准则，原理是求从冗余字典库中寻找到的匹配原子与残差的夹角余弦值。余弦值越大，说明夹角越大，两点相距就越远，相似度就越小。Cosine相似度度量准则的定义为

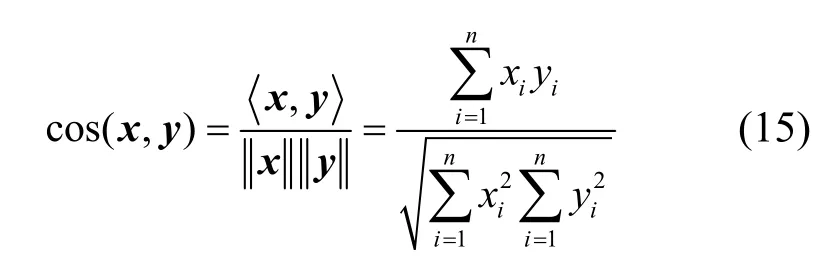
信号重构指的是对通过相似度度量准则得到的最优原子索引集矩阵进行重构计算。算法对原始信号进行重构时，利用Cosine准则度量相似性，不会考虑到原子相似度的变化，不能很好地放大重要向量分量的效果，造成原始信息的部分失真，进而会影响对最优原子索引集的建立，信号的重构效果不好。Cosine相似性表示公共属性的数量除以可能属性的总数，而Tanimoto相似性作为Cosine相似度的扩展，表示公共属性的数量除以2个对象中至少一个对象中存在的属性的数量，且适用于测量稀疏高维数据中的邻近度。Tanimoto可以通过稀疏点积有效地计算非对称数据，在表示向量的接近度时，它同时考虑了向量的角度和长度。这种特性可以更好地保留原始向量分量，捕捉到原子相似度的变化，提升算法的重构效果。所以，引入Tanimoto相似性为

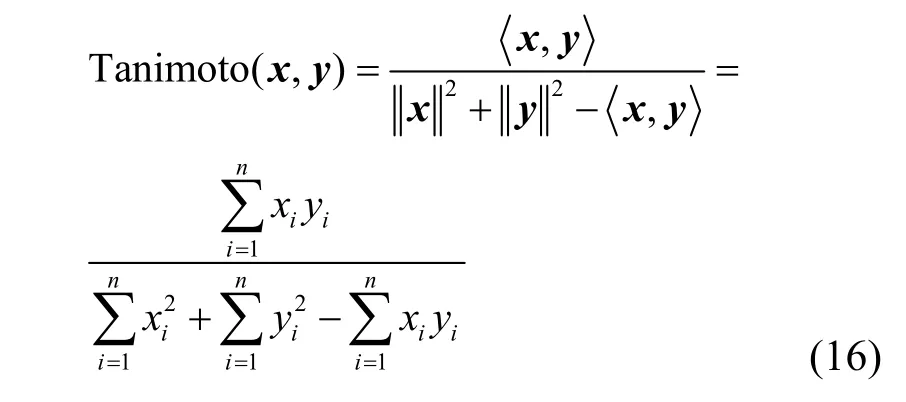
利用Tanimoto相似度度量准则度量相似性时，分子项不变，分母项保留2个对象中至少一个对象中存在的属性特点，从而更多地保留每个向量的原始状态，突出向量中重要的组成元素，真实捕捉到原子相似度的变化。针对任意2个向量x和y，Tanimoto相似性可以最大化地有效运用向量中的数值来求解相似度，解决了Cosine准则在度量过程中导致原始信号部分失真的问题。因此相对于Cosine相似度度量准则，基于Tanimoto相似性的重构算法可以更可靠地区分2个相似的原子，更好地从冗余字典中挑选出与残差信号相似的原子，极大地提升了信号的重构效果。

基于Tanimoto相似性的弱选择正则化正交匹配追踪（T-SWROMP）算法流程如下。

输入原稀疏信号测量值y，测量矩阵Φ，算法最大迭代次数L，重构的误差ε

输出重构信号的原子支撑集，即由中原子的线性组合表示原稀疏信号

1)初始化：初始残差r0=y，迭代次数初始值n=1，算法最大迭代次数L，重构的误差ε，索引值集合Λ=φ，J=φ。

2)弱选择：先计算残差和测量矩阵每个原子之间的Tanimoto相似性，(j=1,…,N)，并从中找出满足式(14)的测量矩阵Φ中原子ϕi对应的索引值i，将其存入索引值集J中。

6)比较算法迭代次数，当n≥L时，停止迭代；比较更新残差和上次迭代残差，当时，停止迭代；否则，令r=rn，n=n+1，转至步骤2)。

4 仿真结果

本节通过仿真，对LS、OMP、ROMP、SWOMP、ARCoSaMP[22]和本文提出的T-SWROMP算法的性能进行了比较。这里分别使用算法的重构率和BER性能来对算法的恢复率和信道估计的性能进行评价。仿真环境中FBMC子载波个数为1 024，星座映射方式为40QAM，原型滤波函数采用Hermite函数，滤波器的重叠因子设定为8，采用IEEE 802.22信道模型,最大径数为6，其信道参数的功率时延谱（PDP,power delay profile）如表1所示。

图3是对原始的和估计的信道参数的功率时延谱的比较，它表明本文所提出的针对FBMC系统的贪婪重构算法能够很好地重构原始的多径信道。

表1 IEEE 802.22信道参数的功率时延谱

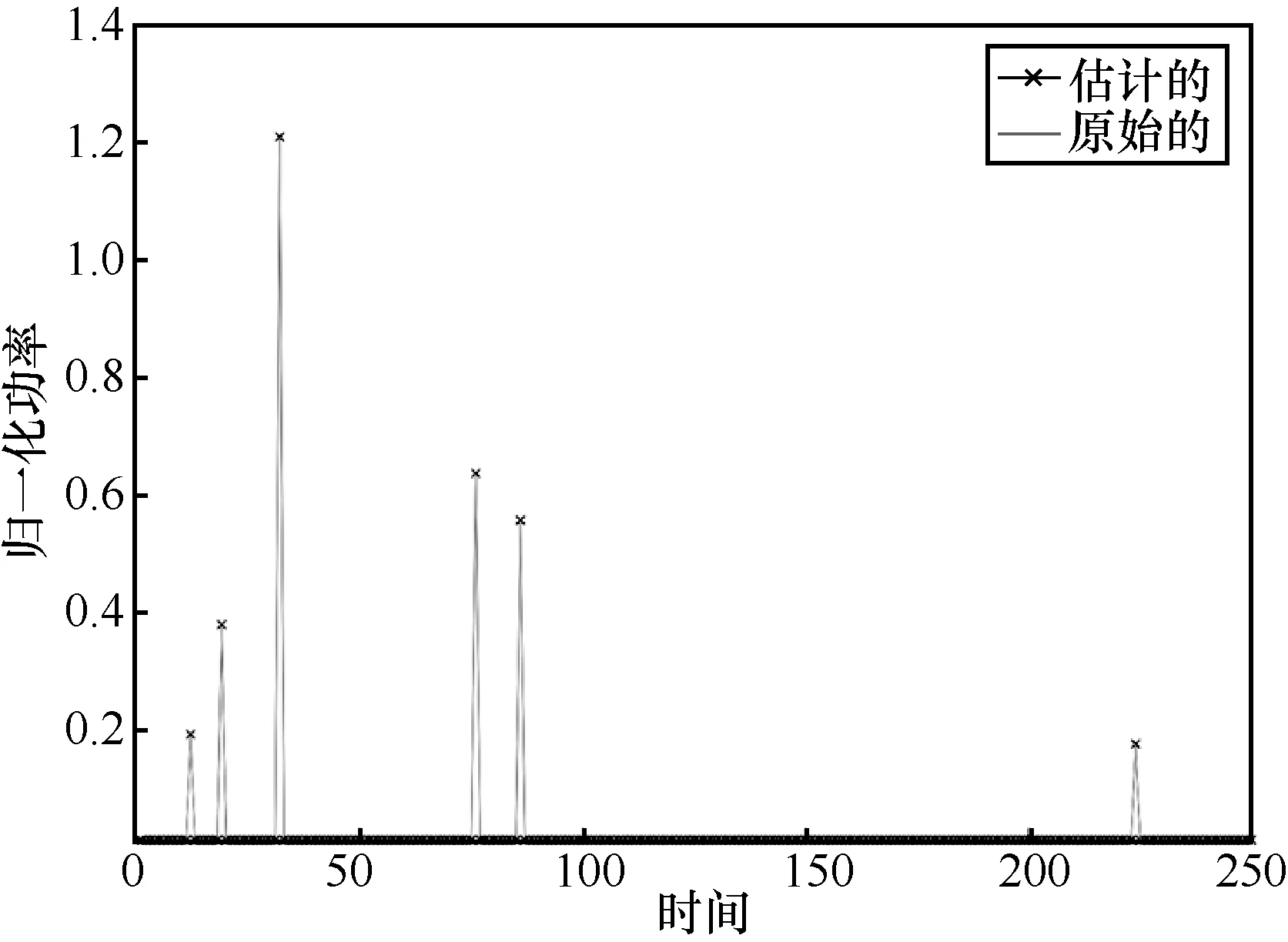
图3 原始的和估计的IEEE 802.22信道参数功率时延谱的比较

本文研究了不同算法在固定信号稀疏度K=8时的重构概率。图4描述了高斯稀疏信号的重构概率曲线。从图4可以看出，当测量值M在5～50的范围内时，所提算法的重构性能优于其他几种算法。

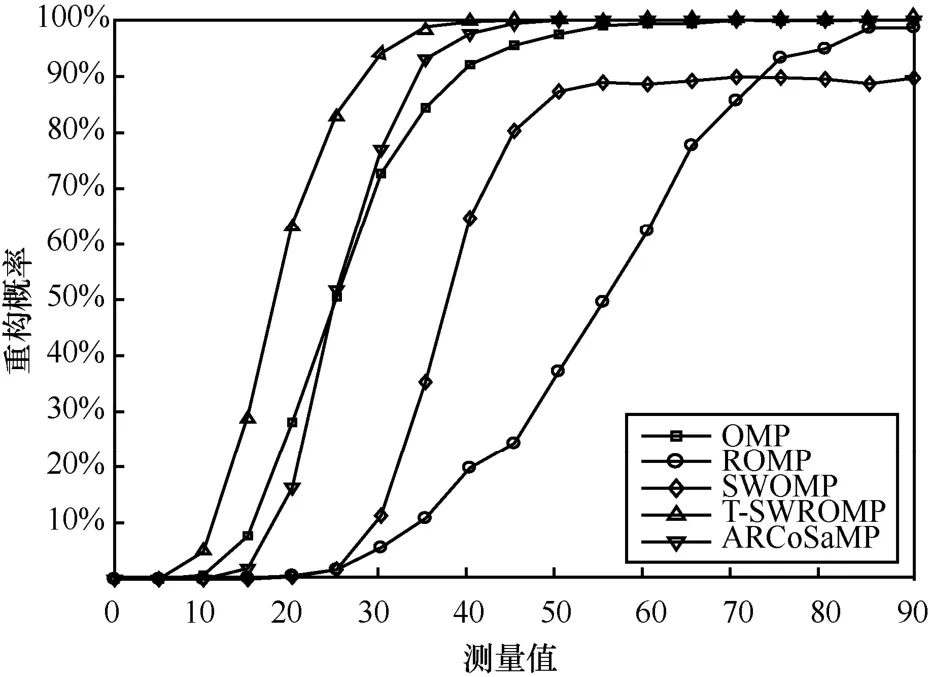
图4 不同重构算法在不同测量值下高斯稀疏信号的重构概率比较(K=8,N=256,Gaussian)

图5显示了FBMC/OQAM系统采用辅助导频结构时的误码率性能随最大多普勒频移的变化。在图5中，随着最大多普勒频移的增大，所提算法与OMP、ROMP、ARCoSaMP算法的估计性能都下降，但是所提算法在估计性能更好的情况下，其变化相对平缓，这说明所提算法对多普勒频移具有较好的稳健性。

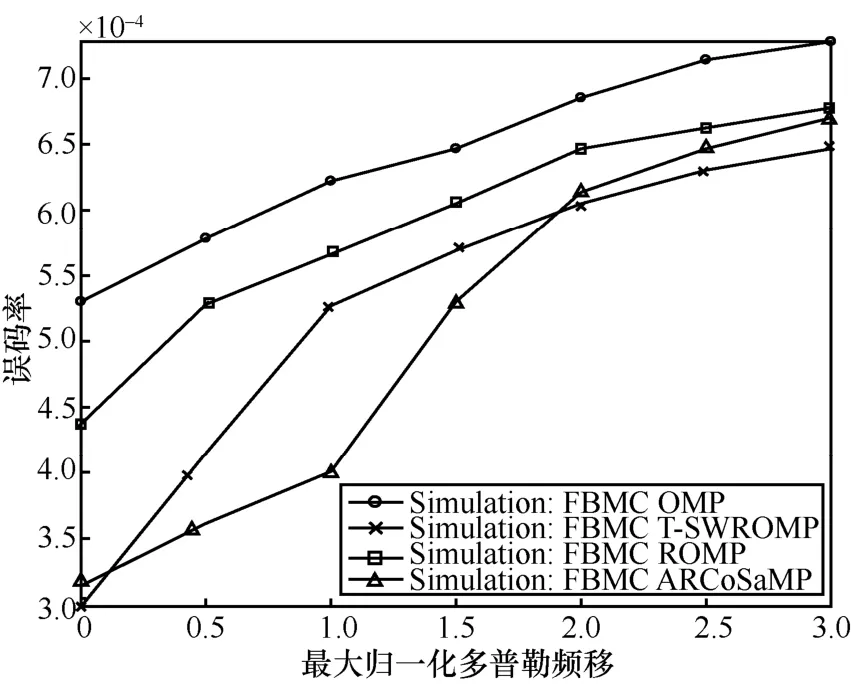
图5 信道估计误码率性能随最大多普勒频移的变化

图6显示了FBMC/OQAM系统采用辅助导频结构时的误码率性能比较。在图6中，FBMC/OQAM系统中采用了基于CS的信道估计，最大多普勒频移设定为10 Hz。与传统LS方法相比，基于CS的信道估计方法可以获得显著的误码率改善。同时，在基于CS的信道估计方法中，所提算法在整个信噪比范围内优于OMP、ROMP和SWOMP算法，与ARCoSaMP算法性能接近。

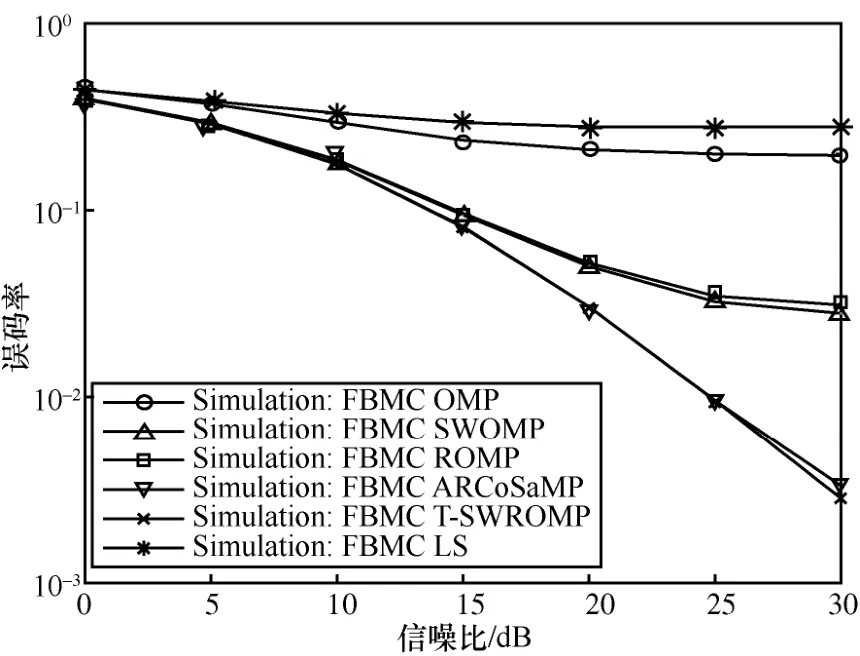
图6 FBMC/OQAM系统下基于辅助导频的信道估计的误码率比较

图7显示了FBMC/OQAM系统采用编码辅助导频结构时的误码率性能比较。同样，在图7中，与LS相比，基于CS的信道估计方法可以获得显著的误码率改善。且在基于CS的信道估计方法中，所提算法在整个信噪比范围内优于OMP、ROMP和SWOMP算法，与ARCoSaMP算法性能接近。

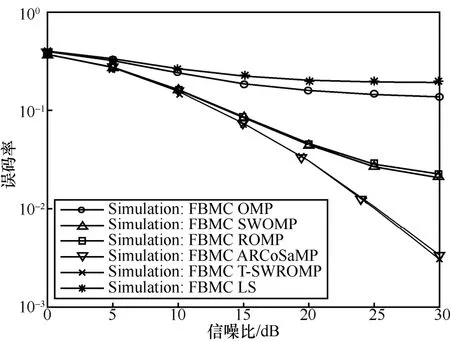
图7 FBMC/OQAM系统下基于编码辅助导频的信道估计的误码率比较

表2给出了仿真中不同稀疏信道恢复算法在配置为i5处理器、3.1 GHz主频、8 GB内存、macOS Mojave(64位)操作系统的PC环境下，进行单次运算所需要的时间。可以看出，在信道稀疏度未知的情况下，T-SWROMP算法在计算复杂度上低于SWOMP和ARCoSaMP算法。由于信道稀疏度未知，迭代次数过多，导致ARCoSaMP和SWOMP稀疏度计算复杂度相对较高。

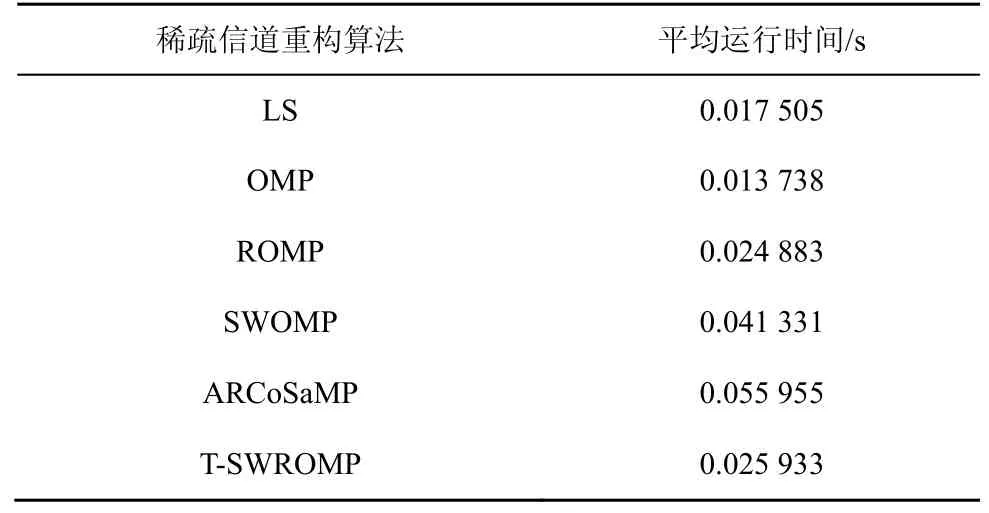
表2 不同稀疏信道重构算法的仿真运行时间

仿真结果表明，在FBMC/OQAM系统中，基于CS的信道估计方法比传统的LS方法能提供更有效的性能。本文提出的基于T-SWROMP的信道估计方法，在不需要信道稀疏度的情况下，可以获得比其他重构算法更好的性能，并且在时间复杂度较低的情况下，具有更好的信道估计性能。

5 结束语

本文研究了在IEEE 802.22稀疏多径衰落信道下基于CS的FMBC/OQAM系统的稀疏信道估计，提出了一种新的基于Tanimoto系数的弱选择正则化正交匹配追踪算法，所提算法结合辅助导频和编码方法，可以实现在未知信号稀疏度的条件下，根据弱选择标准自适应地确定原子候选集的原子个数，进而通过正则化过程从候选集中快速有效地挑选出完成信号重构的最优原子组。同时，在重构信号时，利用Tanimoto度量准则，优化了支撑集的选择，进一步提高了信号的重构精度。仿真结果表明，基于CS的导频方法比传统的LS方法具有更好的误码率性能。在时间复杂度较低的情况下，该方案优于SWOMP算法，并且在未知信道稀疏度的情况下，该方案优于ROMP算法。在FBMC/OQAM传输网络中，T-SWROMP方案是一种有效的稀疏信道估计方法。