智能启发算法在机器学习中的应用研究综述

沈焱萍，郑康锋，伍淳华，杨义先

（1.北京邮电大学网络空间安全学院，北京 100876；2.防灾科技学院信息工程学院，河北 廊坊 065201）

1 引言

1952年，阿瑟萨缪尔开发了具有自学习能力的西洋跳棋程序，并首次提出“机器学习”概念。机器学习伴随着人工智能的发展而发展，Mitchell[1]将其定义为“对于某类任务U和性能度量R，如果一个计算机程序在U上以R衡量的性能随着经验E而自我完善，那么我们称这个计算机程序根据经验E学习”。

根据解决问题所属领域不同，机器学习可分为监督学习、无监督学习和强化学习[2]。在监督学习中，基于带标签的训练数据建立训练模型，常用方法包括人工神经网络（ANN,artificial neural network）、支持向量机（SVM,support vector machine）、极限学习机（ELM,extreme learning machine）、K近邻（KNN,K-nearest neighbor）和决策树（DT,decision tree）等。在无监督学习中，根据不带标签的样本数据建立模型，常用方法包括K-均值聚类（K-means）和自组织映射网络（SOM,self organizing map）等。与监督学习、无监督学习不同，强化学习不知道在某一状态下该做什么动作，而是不断调整每一步策略，通过对学习过程奖励的最大化实现策略最优，常用于路径规划、自动驾驶、棋盘游戏等场景。存储技术的发展和大规模计算能力的提升使针对深度学习的研究受到较多关注，深度学习属于机器学习的一个分支，它们与人工智能的关系如图1所示[3]。

图1 人工智能、机器学习与深度学习关系

建立理想机器学习模型面临各种问题。例如，对于某些模型的构建，个别参数如神经网络权重、核参数等的选取直接影响模型的准确率和泛化能力；诸多聚类算法的性能严格依赖于聚类中心的选取[4]，不仅影响算法的收敛性，对准确率也有很大影响；特征优化是构建机器学习模型的重要步骤，合适的特征集合既能节约系统资源又能准确表示原始数据；集成学习是机器学习领域的重要研究内容，如何选取合适的基学习器，如何将基学习器有效地组合起来是集成学习面临的重要问题；KNN存在计算效率低、存储需求大和易受噪声影响等缺陷。采用数据约简技术可同时解决上述问题。近年来，随着SVM算法的发展和完善，核思想有效应用于非线性模式分析问题中。然而，不同的核函数性能不同，当遇到数据含有异构信息、数据分布不平坦等复杂情况时，单个核函数不能满足实际需求，因此，研究多核学习方法成为当前热点。

综上可知，机器学习模型必须经过优化才能发挥理想效果。优化方法主要包括2类：数学优化方法和智能启发算法。数学优化方法主要依靠目标函数的梯度信息进行寻优，还需要一个良好的起点保证算法成功收敛。对于计算代价高昂的搜索推导问题，基于数学的方法是无效的。常用的数学方法包括牛顿法、动态规划法（DP,dynamic programming）等。近年来，智能启发算法在工程应用中越来越受欢迎，因为它们具有依赖于相对简单的概念并且易于实现、不需要梯度信息、可绕过局部最优、可用于涵盖不同学科的广泛问题等优势[3]。智能启发算法只通过输入和输出来考虑和解决优化问题。换句话说，智能启发算法将优化问题假设为一个黑盒，因此不需要计算导数，这使其在解决各种各样的问题时具有高度的灵活性。数学优化方法和智能启发算法寻优过程对比如图2所示。

对智能启发算法的重要研究工作如下。密德萨斯大学（Middlesex University）的Yang等提出了蝙蝠算法（BA,bat algorithm）[5]、萤火虫算法（FA,firefly algorithm）[6]等，同时对智能启发算法的特征、数学证明及应用场景进行研究；格里菲斯大学（Griffith University）的Mirjalili等提出一系列新的智能启发算法，包括蜻蜓算法（DA,dragonfly algorithm）[7]、鲸鱼优化算法（WOA,whale optimization algorithm）[8]、灰狼优化（GWO,grey wolf optimizer）算法[9]、蚁狮优化（ALO,ant lion optimizer）算法[10]、樽海鞘群算法（SSA,salp swarm algorithm）[11]等，在算法设计的过程中注重探索和利用的平衡；亚伯大学（Aberystwyth University）的研究者采用启发算法，尤其是和声搜索算法（HS,harmony search）进行特征选择、集成约简等。

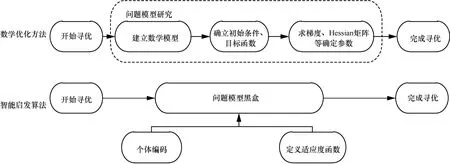
图2 传统优化方法和智能启发算法寻优过程对比

Talbi[12]认为纯启发式算法一般不适用于高维度、复杂的应用场景，提出将数学规划、约束规划、机器学习算法与启发式算法相结合从而改进启发式算法，从算法设计和算法执行两方面进行阐述,同时指出应根据特定的问题设计合适的混合方案。与Talbi的研究不同，本文提出如何将智能启发算法应用于机器学习领域以提高机器学习算法的效率和精度。基于智能启发算法的机器学习建模过程如图3所示，将基于某些特征或样本的训练数据输入核心机器学习算法中，在智能启发算法的帮助下，分析和学习训练集中的数据模式，得到训练好的模型和样本特征。模型的优化过程涉及模型的多次训练，由智能启发算法的迭代次数决定，应用智能启发算法必须确保其收敛。最后，将测试数据输入训练好的算法模型中，得到最终输出结果。

图3 基于智能启发算法的机器学习建模过程

2 智能启发算法分类及建模

2.1 算法分类

智能启发算法可分为2类：基于个体（single-solution-based）的方法和基于种群的（population-based）方法。基于个体的方法指搜索过程从一个候选解开始，在随后的迭代过程中不断改进这个单一候选解，典型算法有爬山法[13]、模拟退火（SA,simulated annealing）算法[14]、禁忌搜索（TS,tabu search）算法[15-16]等。基于种群的方法采用一组解来执行优化，搜索过程从随机初始种群开始，并且种群在迭代过程中得到改进。基于种群方法的搜索过程分为两步：探索阶段和利用阶段。探索阶段指尽可能广泛地探寻搜索空间中有前途区域的过程；利用阶段指在探索阶段获得的有前景区域周边的本地搜索。与基于个体方法相比，基于种群方法中个体相互协助、共享搜索空间信息，避免陷入局部极值，具有更大的探索性。典型算法有粒子群优化（PSO,particle swarm optimization）算法[17]、遗传算法（GA,genetic algorithm）[18]等。

智能启发算法具体分类如图4所示，包括进化算法、基于物理规则方法、群智能算法和基于人类行为的方法[7]。进化计算模拟自然界生物进化过程，采用“优胜劣汰”达到进化目的，典型算法包括遗传算法、进化策略（ES,evolution strategy）[19]、基因编码（GP,gene coding）[20]和差分进化（DE,differential evolution）算法[21]等。基于物理规则（physics-based）的方法指通过模拟自然界中的物理现象概括出的启发式算法。一组代理通过某种物理规律，如重力、运动定律、光线投射、电磁力、惯性力等在搜索空间中移动，并根据一定规律相互通信。典型算法有引力搜索算法（GSA,gravitational search algorithm）[22]、收费系统搜索算法（CSS，charged system search）[23]、中心力优化（CFO,central force optimization）算法[24]和大爆炸（BBBC,big-bang big-crunch）算法[25]等。群智能（SI,swarm intelligence）算法从鸟类、蚂蚁等动物行为中获得灵感，具有通过个体间交互解决复杂任务的能力，典型算法包括粒子群优化算法、蚁群优化（ACO,ant colony optimization）算法[26]、蜂群（ABC,artificial bee colony）算法[27]和布谷鸟搜索（CS,cuckoo search）算法[28]等。群智能算法和进化算法在种群迭代方式上不尽相同，群智能算法侧重群体中个体之间的协作，而进化算法侧重个体的进化。还有一些受人类行为启发（human-based）的智能搜索方法，如教与学优化（TLBO,teaching learning based optimization）算法[29]、和声搜索[30]、禁忌搜索和组搜索优化（GSO,group search optimizer）[31]等。

图4 智能启发算法分类

值得一提的是，无免费午餐（NFL,no free lunch）定理[32]在逻辑上证明了单一智能启发式算法不能解决所有优化问题。换句话说，一个特定的智能启发方法可能在一组问题上显示出较好的性能，但在另外一组问题上可能表现出较差的性能。因此，当前智能启发算法需要不断被改进，也需要提出新的智能启发算法。

2.2 算法建模

2.2.1 个体编码

采用智能启发算法首先需要考虑个体编码问题，这将直接影响算法搜索的精度和效率。

有效的编码方式能在保证算法执行效率的前提下简单明了地表示问题的解，并支持后续算子的各种操作变化。常用编码方式优缺点及应用场景如表1所示。智能启发算法大多采用矢量方式编码，包括数值编码和符号编码。数值编码即根据实际需求或算法特点采用二进制或实数方式编码。经典遗传算法本身采用二进制编码，大多数智能启发算法基于实数编码被创建。智能启发算法还可采用符号编码，有时要求的解仅仅是一种类型信息，并不具有任何数值意义，可采用特殊意义的符号组合表示此类问题的解。

目前的启发算法能解决相关参数确定和类型选择问题，但无法解决多类型组合及嵌套问题，基于非线性结构编码的启发算法应运而生。例如，对于遗传算法、遗传规划（GP,genetic programming）[33]，个体可采用树形结构、堆栈结构等编码方式解决此类问题。

个体编码长度由实际问题维度或精度决定，一般来说个体表达不能太长，否则不仅影响算法搜索效率，还会使算法寻优性能下降[34]。不管采用何种编码方式，都在迭代结束前对产生的新个体进行评估。

2.2.2 适应度函数定义

适应度函数的定义对于智能启发算法建模至关重要，直接决定了收敛结果。适应度函数用于评估个体在迭代过程中的优劣，指引算法向何处搜索，通常根据实际问题的需求进行定义，例如对于分类问题，准确率、错误率、召回率、F值可作为适应度函数评估标准；对于回归问题，可以定义均方误差作为适应度函数。本节以用于分类的监督学习算法为基础，如快速学习网络（FLN,fast learning network）[35]等介绍启发算法进行优化时几种常见的适应度函数，其定义如表2所示。表2中，w1和w2分别表示不同评估度量的权重，必须保证不同评估度量的取值范围是一致的。采用此种方式定义的适应度函数应事先确定搜索目标的极大值或是极小值，例如对于入侵检测问题，在进行特征选择的同时提高检测性能，为了获得最佳适应度值，个体必须最大化检测率、最小化虚警率和特征个数。为了达到最佳适应值，检测率的权值应设置较高，虚警率和表示特征个数的权重应设置相对较小，因为检测率是相对重要的目标度量。

表1 编码方式优缺点及应用场景

还可根据实际需求定义带约束条件或多目标优化的适应度函数。采用罚函数等方法将约束优化问题转化为无约束优化问题。如果涉及多种度量，可通过表2所示的加权适应度函数将多目标优化转变为单目标优化问题。此外，还可定义多目标适应度函数，目前已经提出多种实现多目标优化的方法[7]。智能启发算法试图尽可能精确地找到一组称为帕累托最优集的解。

对于具体问题，将其看作一种优化搜索问题，研究其评估标准，采用智能启发算法定义合适的目标函数进行搜索，可起到事半功倍的效果。智能启发算法建模流程如下。

1)设置算法相关参数，例如迭代次数、种群规模等。

2)按照个体编码规则初始化种群。

3)根据适应度函数找出初始种群最佳个体。

4)按照个体变异规则产生新一代种群。

5)根据适应度函数计算新一代种群最佳个体。

6)重复步骤4)和步骤5)，直到迭代次数终止或满足最佳适应度值。

7)输出最优解。

2.2.3 复杂度分析

智能启发算法属于黑盒优化算法，不同启发算法的迭代有其自身固定的操作环节。例如，对于PSO算法，个体需要通过速度更新式计算粒子新的速度，根据速度求出粒子的最终位置；对于差分进化算法，个体位置更新需经历变异、交叉和选择等过程。由分析可知，同一类别不同启发算法迭代规则虽不尽相同，但由此产生的复杂度差别并不大。算法复杂度主要由适应度函数决定，对每一代种群中的每个个体都需计算适应度值，假设其复杂度为O(fitness)，则基于启发算法优化模型的算法复杂度为O(fitness)×sizepop×NoIter，其中，sizepop为种群规模，NoIter为迭代次数。

3 智能启发算法在机器学习中的应用

建立理想机器学习模型面临各种问题，例如，对于多核学习任务，传统的多核学习方法通常将问题表述为核函数和分类器的最佳组合的优化任务，通常是一些很难解决的具有挑战性的优化任务[36]；而采用智能启发算法对机器学习算法模型进行优化，可以避免将问题复杂化，从侧面以仿生学的方式解决问题。基于智能启发算法的机器学习模型优化体系如图5所示，包括神经网络等参数结构优化、特征优化、集成约简、原型优化、加权投票集成、核函数学习等。

表2 智能启发算法常用评估度量及适应度函数定义形式

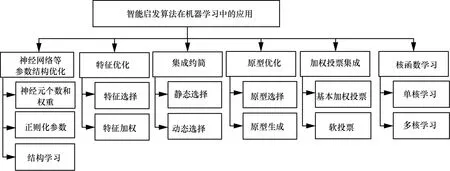
图5 基于智能启发算法的机器学习模型优化体系

3.1 神经网络等参数结构优化

基于神经网络等机器学习算法建立的模型必须经过调参才能发挥理想效果，深度学习方法也是如此。由于任何一个网络模型都无法适用于所有数据集，因此，将深度学习方法应用于新数据集之前，必须先选择一组适当的超参数[37]。对于卷积神经网络（CNN,convolutional neural network），这些超参数包括网络层数、每层隐藏节点数、层的激活函数、网络中层的排列等。为一组新的数据集选择新的网络拓扑可能是一项耗时的任务。

在ELM中，随机选择输入权重，并通过分析计算输出权重。由于输入权重和隐藏偏差确定的随机性，ELM可能需要更多的隐藏神经元。Ahila等[38]提出了一种混合优化机制，将离散值粒子群算法与连续值粒子群算法相结合，对输入特征子集选择和隐藏节点数进行优化，以提高ELM的性能。Zhu等[39]采用差分进化算法确定ELM输入和输出权重。Zhang等[40]提出一种新的memetic算法优化ELM相关参数，将局部搜索策略嵌入全局优化框架中以获得最优的网络参数。Camilleri等[41]采用网格搜索和一种简单遗传算法优化决策树ID3相关参数，包括单点最小增益、树的最大深度和最小分割标准。Kardan等[42]提出一种基于生物地理学优化（BBO,biogeography based optimization）算法的改进K近邻的混合算法。BBO同时对特征选择、特征权重和邻域大小进行优化。Costa等[43]提出一种基于最优路径森林算法（OPFC,optimum-path forest algorithm）的入侵检测模型，采用智能启发方法估计概率密度函数，所用智能启发方法包括蝙蝠算法、萤火虫算法、引力搜索算法、和声搜索方法和粒子群优化算法。实验结果表明，所有智能启发方法都比穷尽搜索方法快，但BA和PSO在效率和有效性方面都取得了最好的效果。结构学习是贝叶斯网络（BN,bayesian network）研究领域的一个重要问题。为找到一个基于训练样本的最优结构，人们提出许多方法，Gheisari等[44]提出一种基于粒子群优化的BN结构学习算法。支持向量机是近些年应用较广泛的机器学习算法，为了构造一个精确的支持向量机分类器，必须确定核函数、核参数和软边界常数（也称为正则化参数）。对于参数的选取，智能启发算法的应用提供了一些思路。目前，有大量关于SVM相关参数的优化方案[45-46]。智能启发算法优化参数如表3所示。

随着计算机技术的发展，神经网络、进化算法等智能计算方法已经取得了巨大的进步，它们都是将生物学原理应用于科学研究的理论成果。二者可以相互补充、彼此强化，从而获得更强大的表现和解决实际问题的能力[47]，它们的融合产生一种新的神经网络称为进化神经网络。进化网络通常是前馈网络，需要研究其他类型网络的进化算法，目前的研究大多是基于特殊情况，尚未形成通用的方法论，需要与粒子群等其他优化算法进行比较，而且计算复杂，需要改进演化过程，特别是研究并行进化算法的应用。

表3 智能启发算法优化参数

3.2 特征优化

降维是建立有效机器学习模型的关键步骤。通常来说，降维方法有以下2种：特征选择和特征提取。特征选择可去除不相关或冗余特征，在进行分类时获得比原样本集相当或更好的效果。特征提取试图通过组合原始特征来降低维数，这种方法试图将信息损失降到最低，但是通常会丢失原始特征。

特征加权可以看作特征选择的泛化[48]。假设原始特征为F={f1,f2,…,fH}。特征加权算法试图为每个特征f∈F分配一个通常在[0,1]的权重wf，权重反映了特征f针对特定问题的相关程度。特征选择算法每个特征的权重为wf∈{0，1}，wf=1 时特征f被选中，否则被丢弃。相比特征选择硬性地选择一部分特征，特征加权是一种特征选择软方案。有些特征选择算法是根据特征权重的大小选择合适的特征子集，特征权重较小的被移除。这里的特征优化指特征选择和特征加权。

常用的特征选择方法包括过滤法（filter）和封装法（wrapper）。过滤法与后续算法无关，根据原始数据集的统计性能选择特征。常用的过滤法包括[49]：基于距离的方法，如relief等；基于信息度量的方法，如信息增益（IG,information gain）；基于依赖性度量的方法；基于一致性度量的方法。封装法与后续学习算法相结合进行特征选择，例如根据后续学习算法的准确率选择合适的特征。常用封装法包括完全搜索法、启发式搜索法、随机搜索法等。封装法以后续学习算法为指引开展工作，通常比过滤法有更好的学习效果。基于智能启发算法进行特征选择（特征加权）大多属于封装法。

贪婪搜索和relief等特征优化方法要么易陷入局部最优，要么只进行特征排序，并不考虑特征交互。而进化计算技术具有很强的全局寻优能力，在进行特征选择问题上显示出了比其他方法更大的优势。Kashef等[50]提出采用改进二进制ACO进行特征选择，特征被视为图中的点，要求蚂蚁必须访问所有特征，采用几种统计度量作为启发式函数检查图中边缘的可见性。Zelenkov等[51]采用遗传算法进行特征选择，选用准确率作为适应度函数。Diao等[52]对应用于特征选择的10种不同启发算法进行比较，结果表明所有算法都可以找到质量较优的特征子集，其中模拟退火算法和禁忌搜索算法可以达到更好的评估适应度值。Mateos等[53]提出一种基于进化计算的KNN改进规则，统一2个经典加权范式，即对每个邻居的贡献度和数据特征的重要性同时进行调整，以更好地识别新的实例。文本自动聚类已成为一种有效的文本分析方法，Bharti等[54]在聚类前采用二进制粒子群优化算法进行特征选择，采用添加变异取反策略改进二进制粒子群算法增强搜索性能。Li等[55]采用改进灰狼算法进行特征选择，采用GA确定灰狼初始种群位置。Zhang[56]借用SA、混沌相关思想改进FA增强全局搜索能力，并将其应用于分类和回归模型中进行特征选择。

如果要选择的特征数量是固定的，可以选用十进制编码；如果要选择的特征数量事先没有确定，则采用常规的二进制编码。值得一提的是，在确定基学习器相关参数时，可采用特征选择算法在进行特征选择的同时对支持向量机的正则化参数、核参数进行优化，因为特征子集的选择对适当的内核参数有影响，反之亦然。

大量实验表明，基于智能启发算法的特征优化方法通常与基于filter的度量方法结果保持一致。不同的启发算法能否识别出不同的特征子集，从而采用特征选择集成构造出更高质量的特征子集是值得进一步研究的。实验结果还表明，每种启发算法在处理不同的数据集时可能有其自身的优势和弱点，可以开发一种元框架，动态地识别合适的算法，以形成一种更智能的、混合的特征优化方法。

3.3 集成约简

多分类器集成系统（MCS,multiple classifier systems）的构建由三部分组成：子模型产生、子模型选择及子模型的集成方式[57]。集成约简（ensemble pruning）又称集成选择（ensemble selection），是子模型创建和子模型集成的中间环节，集成约简的主要工作是减少将要集成的子学习器的数目。假设分类器池为C={c1,c2,…,cM}，M为所有分类器的数量。集成约简的目的是寻找一组分类器C'⊂C，使基于C'在测试集上的性能类似或优于基于C在测试集上的性能。减少子学习器数量可以消除部分运行开销，使集成处理更快，同时也意味着较小的内存和存储需求；删除冗余成员也可改善集成系统子学习器的多样性，进一步提高系统预测精度。目前常用的集成约简算法包括基于某度量的子模型排序方案、基于聚类的集成约简方案和基于优化算法的约简算法等。Cruz指出集成选择分为静态选择和动态选择，在静态选择中，选用固定的子模型子集对测试样本进行预测；而动态选择对于不同的测试样本选用的子模型子集不同。目前存在的大部分集成约简技术都属于静态选择。

集成约简和特征选择思想类似，都是采用某种方法选择原始集合的子集，Zhou等[58]提出一种基于GA的集成约简模型，给每个神经网络即子分类器赋予一个权重，该权重表示将该神经网络包含在集成中的可能性，将权重大于预设阈值的子模型加入集成中。实验结果表明，使用一定数目的子学习器比使用所有的子学习器效果更好。Diao等[59]将集成学习预测比作训练样本，将分类器视为特征，将特征选择相关思想应用在分类器集成约简，采用全局启发式和声搜索算法进行集成约简。Shen等[60]采用二进制蝙蝠算法对投票极限学习机集成算法进行约简，并应用于入侵检测领域，验证了Zhou提出的“many could be better than all”相关思想。Krawczyk等[61]也将集成约简问题看作搜索问题，提出一种基于萤火虫算法的one-class分类器集成约简框架，基于聚类的集成修剪思想，发现类似的分类器组，并用一个相关的代表来代替它们，最后将选出的分类器进行权重组合。Hu等[62]提出一种分布式入侵检测框架，采用在线AdaBoost算法在每个节点上构造局部检测模型，采用PSO挑选合适的局部模型进行整合，最终采用支持向量机进行全局检测。

一般的集成约简策略都是通用的，属于框架方案适用于任何子模型。在未来的工作中，针对不同的应用场景选择相适应的子模型，并选用适当的评估标准，如准确率、差异性度量等多目标适应度评估标准，生成适合的集成约简方案需要进一步考虑。如何扩展并改进现有约简算法以解决机器学习中存在的概念漂移、超参数选择等问题也需要进一步考虑[63]。

3.4 原型优化

原型优化用来实现数据约简或原型简化。由于近邻（NN,nearest neighbor）模型存在存储需求大、易受噪声影响等问题，常采用NN模型指引数据约简。假设样本表示为(xi,yi)，其中xi=(xi1,xi2,…,xiD)∈RH，H为特征总数，yi表示样本标签，NN模型一般采用欧氏距离评估样本相似度，如式(1)所示。

其中，d(xi,xj)表示样本xi和xj的欧氏距离，xir表示样本i的第r个特征。

假设P表示一组原始数据，原型优化的目的是从原始数据P中寻找一组约简子集P'使|P'|<<|P|，约简子集P'可能包含和原始数据P中相同的样本，也可能包含根据原始样本组成的新样本。原型优化指从原始数据集生成一组原型，使基于生成数据训练的近邻模型可以接近（或优于）基于原始数据生成的学习模型。原型优化可分为原型选择（PS,prototype selection）和原型生成（PG,prototype generation）技术。PS技术用来识别原始数据集的最佳子集，PG关注创建一组可以表示原始数据的新对象。与特征选择相同，PS和PG技术也可以分为filter和wrapper这2种[64-65]。常见的PS算法包括剪辑近邻法（ENN,edited nearest neighbor）[66]与压缩近邻法（CNN,condensed nearest neighbour）[67]。传统的PG方法包括学习矢量量化[68]、bootstrap技术[69]和高斯混合方法[70]。进化计算是一种新的原型生成方法。

Nanni等[71]提出一种基于PSO的原型约简方法。算法流程类似于对随机森林中随机子空间的处理。在训练阶段，重复生成原型多次，然后使用每个训练模型对每个测试样本进行分类，最后通过多数投票规则将分类结果组合起来。Hu等[72]提出一种PSO多目标优化原型生成方法。Triguero等[73]介绍了一种位置调整的原型生成方法，采用差分进化方法对原型进行定位优化。Rezaei等[74]采用重力搜索算法生成原型，利用分层策略提取初始对象。实验表明，基于GSA的原型生成技术可以提高KNN分类器的性能。

Perez等[75]采用混合差分进化算法和CHC遗传算法同时进行特征选择、实例选择、特征权重和实例权重调整。Derrac[76]采用一种协同进化算法同时优化样本和特征权重并进行原形选择。Escalante等[77]介绍一种基于遗传规划的原型生成技术，所提方法将多个训练样本通过算术运算结合起来生成目标原型，采用1NN作为评估分类器。Verbiest等[78]提出一种原型选择框架，将多个最佳原型子集进行集成，给出4种最先进的基于进化的PS方法，包括世代遗传算法（GGA，generational genetic algorithm）、稳态遗传算法（SSGA，steady state genetic algorithm）、稳态memetic算法、扩展GGA的自适应实例选择搜索算法。GGA和SSGA都遵循进化算法一般方案，不同之处在于SSGA在每代中只生成2个新的个体，而GGA则取代一部分个体；稳态memetic算法即在SSGA算法中添加优化策略。4种基于进化算法进行原型选择的适应度函数定义如表2中F4所示。

为了增加算法在海量数据上的执行效率，应着重于研究进化算法的分布式，如MapReduce的编程模型。了解每种原型优化方法的主要优点，根据所解决的问题选择合适的原型优化方法也是需要进一步考虑的问题。

3.5 加权投票集成

对3.3节中提到的集成学习的第三个步骤子模型的集成方式，即子模型的组合策略，使用最多的是多数投票和加权投票组合策略。多数投票根据投票最多作为最终预测结果，由于概念简单、直观、有效而被广泛使用。然而不同的子学习器发挥的作用不同，因此可采用加权投票的方式进行组合。

根据分类器的输出（标签类别或概率类别），加权投票集成可分为基本加权投票和软投票系统[72]。假设分类标签yn为yn∈{ω1,…,ωD}，其中，ωj表示类别j，D为类别总数。C={c1,c2,…,cM}，ci(i=1,…,M)表示独立的分类器，M为分类器总数，则

其中，H(xT)表示样本xT的预测类别，pij(xT)为样本xT被分类器ci判断为ωj的概率，wi表示分类器ci的权重。

对于基本加权投票，如果分类器ci对样本xT的预测为类别ωj，则pij(xT)=1，否则pij(xT)=0。当遇到二分类问题(yn∈{-1,1})时，式(2)可写为

其中，fi(xT)表示样本xT被分类器ci预测的类别。

对于软投票系统，根据加权级别不同可分为分类器级别加权、样本级别加权和类别级别加权[79]。分类器级别加权只对要集成的基学习器分配权重，总体性能良好的基学习器的权重较高；针对每个样本对分类器影响不同，可对样本给予适当权重；对于类别加权，考虑到不同子学习器在不同类别上的性能不同，为每个基学习器在不同输出类别上分配不同的权重。

加权投票可以看作一种优化问题，可采用智能启发算法解决。Aburomman等[80]提出了一种新的集成构造入侵检测模型，采用不同K值的K近邻方法和不同参数的SVM作为基分类器，采用粒子群算法产生的权值对其进行集成。采用局部单峰采样（LUS,local unimodal sampling）方法作为元优化器，为粒子群优化算法寻找更好的性能参数。Zhang等[81]采用C4.5、朴素贝叶斯（NB,naive Bayesian）、贝叶斯网络和K近邻方法作为基分类器，采用差分进化算法确定加权投票的权值。Onan等[82]基于一种多目标优化的差分进化算法确定投票权值，采用逻辑回归（LR,logistic regression）、朴素贝叶斯、线性判别分析、逻辑回归和支持向量机作为基学习器，实验结果表明该方案比传统的集成学习方法如AdaBoost、Bagging、随机子空间和多数投票等具有更好的预测能力。Zelenkov等[51]采用GA进行特征选择的同时，也用其进行权重组合学习。Ekbal等[83]采用GA构造基于加权投票的分类器集合解决命名实体识别（NER,named entity recognition）问题，以最大熵（ME,maximum entropy）、条件随机场（CRF,conditional random field）和SVM作为基本分类器。结果表明，基于GA的投票集成策略优于单个分类器、3种传统集成方法和一些现有集成技术。

对于异构集成学习模型，由于不同子模型性能不同，对子模型的选择是加权投票集成的关键问题。除此之外，可能需要同时优化多种度量确定最佳集成组合，采用多目标优化技术是解决此类集成优化的关键。

3.6 核函数学习

核方法是机器学习领域有效的学习方法，主要用来解决低维空间线性不可分问题。采用核方法的好处在于可以处理任意维数的特征空间，而不需要计算其到特征空间的映射，避免复杂的内积计算。核函数可表示为一特征空间的内积，假设K(xi,xj)为核函数，向量xi和xj在高维特征空间的内积可表示为K(xi,xj)=<φ(xi),φ(xj)>，其中φ(x)表示向量x到高维空间的映射。任意满足Mercer定理的函数都可以作为核函数。典型核函数包括线性核函数、多项式核函数、径向基核函数、sigmoid核函数等，其中径向基核函数又称为高斯核函数是最常用的核函数。然而，由于样本可能包含异构信息或者表示方式不同，使用单个预定义核函数通常是不够的。因此，存在核组合方法的大量研究，即多核学习（MKL,multiple kernel learning）。不管采用单核学习还是多核学习，都需确定相关核参数，因为其隐式定义了高维特征空间的结构，从而控制最终解决方案的复杂性，对于多核学习还需确定相关核函数系数。线性多核函数是最常见的多核函数形式[84]，如式(4)所示。

其中，n表示核函数的个数，s表示核函数的序号，sω表示第s个核函数的系数。SVM是核方法成功应用的典型。为了确定核函数及相关参数，大量核方法通常基于SVM展开研究，将目标函数转化为不同的优化问题，通过不同的优化方法求解。采用智能启发算法求解核函数不失为一种简洁的方案。Gauthama等[85]针对SVM参数设置，包括惩罚参数项和高斯核参数以及特征选择问题，提出一种基于超图遗传算法（HG-GA,hypergraph based genetic algorithm）的自适应稳健入侵检测技术。Zhang等[86]提出采用蚁群优化算法优化SVM相关参数。Kuang等[87-88]分别采用遗传算法和混沌粒子群优化算法优化SVM相关参数，建立基于KPCA进行特征提取的入侵检测模型。当前存在的智能启发算法不断被改进，Bamakan等[89]提出一种基于时变混沌粒子群优化算法进行特征选择和确定SVM参数的入侵检测模型，采用检测率和误报率2种度量定义适应度函数。Bao等[90]提出一种基于PSO和模式搜索（PS,pattern search）的memetic框架对SVM参数寻优，其中，PSO用来搜索全局空间，PS进行局部探寻，并采用一种概率选择策略平衡二者关系。Avci等[91]采用GA优化基于小波核函数的核参数及极限学习机相关系数。

Ma等[84]提出基于自适应蜂群（SABC,self-adaptive artificial bee colony）算法的多尺度高斯核极限学习机模型。采用多种高斯核函数相结合的方式作为核极限学习机的核函数，指出多种高斯核函数的结合比用单一高斯核函数更灵活。SABC用来确定正则化参数和核参数以及多个核函数的权重值。和Ma的分类器相关的多核学习相比，Niazmardi等[92]采用和分类器无关的多核学习方法，提出采用PSO评估组合核和理想核的相似度进行多核学习，采用3种基于核的相似性度量，即核对齐（KA,kernel alignment）、中心核对齐（CKA,centered kernel alignment）和希尔伯特–施密特独立准则（HSIC,Hilbert-Schmidt independence criterion）进行评估。

多核学习方法假定基础核函数是预先确定的，目前大多数MKL算法采用复杂的优化技术，只能解决二分类问题[92]；而采用启发算法进行多核学习可同时优化基本核参数及其组合系数。在已有核函数学习框架中，评估核函数的非线性组合以及核相似性度量是需要进一步研究的方向。

4 结束语

本文结合机器学习算法在实际应用中面临的问题，对智能启发算法在机器学习中的应用进行总结，从对神经网络等参数结构的优化、特征优化、集成约简、原型优化、加权投票集成和核函数学习等方面介绍智能启发算法的应用场景，为解决问题提供一个新的思路。采用智能启法算法解决问题是一个相对较新的领域，常和其他技术相结合使用。另外，智能启发算法本身也可以直接应用在某一领域，例如传统的聚类算法一般基于梯度下降法实现，然而由于求解易陷入局部极值，产生的结果并不准确。1990年，研究者们开始尝试采用自然启发方法实现聚类，Nanda等[93]研究基于自然启发式的聚类分析方法近二十年，将单目标函数启发算法和多目标函数启发算法在聚类中的应用进行综述。对启发算法还有许多新的研究领域。

1)无免费午餐定理指出没有一种优化方法适用于所有问题，根据具体应用场景研究相适应的新的智能启发算法是研究者们一直努力的方向。考虑不同算法的优缺点，将不同算法的搜索策略进行组合产生新的算法也是研究者们研究的热点。

2)智能启发算法相关参数将不同程度影响算法性能，如何调整参数以提高算法性能是一项重要任务。

3)尽管智能启发算法在实践中很有效，但在理论上还没有经过数学上的分析证明[94]。尝试用一些数学工具如马尔可夫链理论、动态系统等方法证明算法的有效性是学者们努力的方向。

4)由于深度学习算法训练时间过长，如何采用智能启发算法在合理的时间内优化大数据背景下的深度学习模型是一个挑战[95]。如采用基于GPU并行计算的智能启发算法或许可加快模型的训练速度。

5)在科学、工程、工业和商业等领域有许多优化问题待解决，研究某种应用场景下相适合的启发算法是研究者们要考虑的问题。