钢质海洋渔船中剖面结构优化设计

，

(1 大连海洋大学航海与船舶工程学院，辽宁 大连 116023;2 大连市渔船安全技术工程技术研究中心，辽宁 大连 116023)

2017年中国渔船总数量已达101.11万艘[1]，其中大量的“老旧木”渔船及不断增长的海运需求对环境的污染日渐显著，发展绿色渔船是渔船未来必经之路。相比于其他绿色渔船优化的方法，本文的结构优化设计，其优势在于不需要对渔船型线和渔船布置进行改变，可直接减少造船时所用钢材及减小船舶自重，从而达到优化船舶的目的[2]。

20世纪60年代中期，Moe等[3]发表了关于汽车运输船甲板优化的论文，首次把数学规划论应用于船舶结构领域。根据各国相应的设计规范要求不同，国外部分学者采用模拟退火法[4]对船舶中横剖面结构进行结构优化设计，Sekulski等[5]选取板厚度、纵向加劲肋和横向框架的尺寸和间距作为设计变量，应用遗传算法对某高速双体客船中剖面结构进行多目标优化。近年来国内多数学者采用智能算法进行研究，如遗传算法、粒子群算法、蚁群算法等。钦伦洋[6]应用控制算法与有限元计算和规范约束对某三体船进行拓扑优化设计，达到了船舶结构轻量化设计研究的目的。邓良[7]将灵敏度分析、人工神经网络、最优化方法和有限元法集成应用到船舶结构轻量化研究中，最后全船的质量与未优化之前相比减轻了11.8%。郭晓[8]基于极限承载能力应用多目标优化方法，对江海直达船中剖面结构进行优化设计并表明结果可行。混合整数、离散规划、模拟退火等算法试图解决船舶优化中的计算速度慢、计算复杂等问题，但没有明显提高对整数与离散型变量处理的有效性[9]。

针对上述问题，本研究采用高斯变异算法对蚁群算法进行改进，达到增强蚁群算法寻优速度，简化计算过程的目的。在不影响原有渔船的静水力稳性、航行操作性能以及鱼舱舱容及布置的前提下，将中横剖面上主要构件的板厚、剖面积、件间距等作为设计变量，以单位长度中剖面结构质量轻量化为目标函数，根据《钢质海洋渔船建造规范(2015)》[10]提取约束条件，采用改进蚁群算法对某海洋渔船中剖面结构进行优化设计。

1 钢质海洋渔船中剖面结构优化设计模型

1.1 已知条件

(1)渔船主尺度。已知条件主要包括以下数据：船长L(m)；垂线间长LPP(m)；型宽B(m)；型深D(m)；设计吃水d(m)；载重量W(t)；设计航速V(m/s)；方形系数Cb。

(2)中横剖面参数。对43 m流刺网渔船中第4号鱼舱舱段中剖面结构进行优化。中剖面参数包括中剖面各构件的尺寸、间距等，代号及名称见表1，示意图如图1。

表1 中横剖面纵向构件参数表

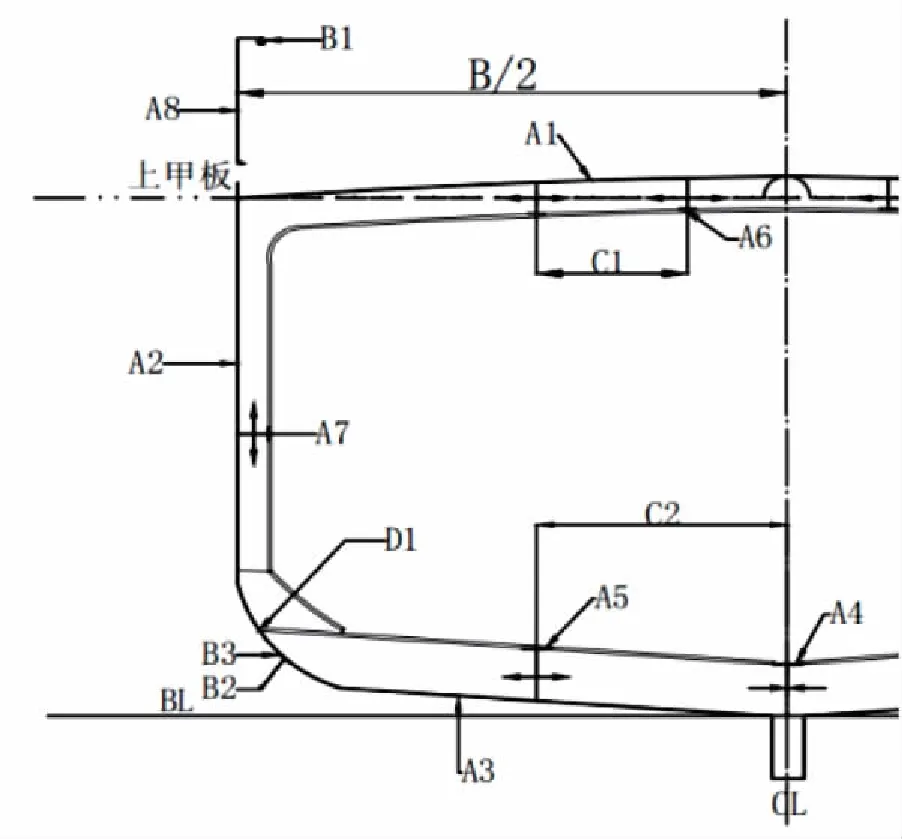
图1 中横剖面结构参数示意图

1.2 变量选取

通过对船中第4号鱼舱舱段中横剖面所需满足的总纵强度、局部强度及构件尺寸进行分析，在该剖面上选取单位长度的纵向板材和纵向型材的板厚、剖面积及件间距等18个设计变量，其中，构件板厚代号及名称、剖面积代号及名称、件间距代号及名称见表2，示意图如图2。

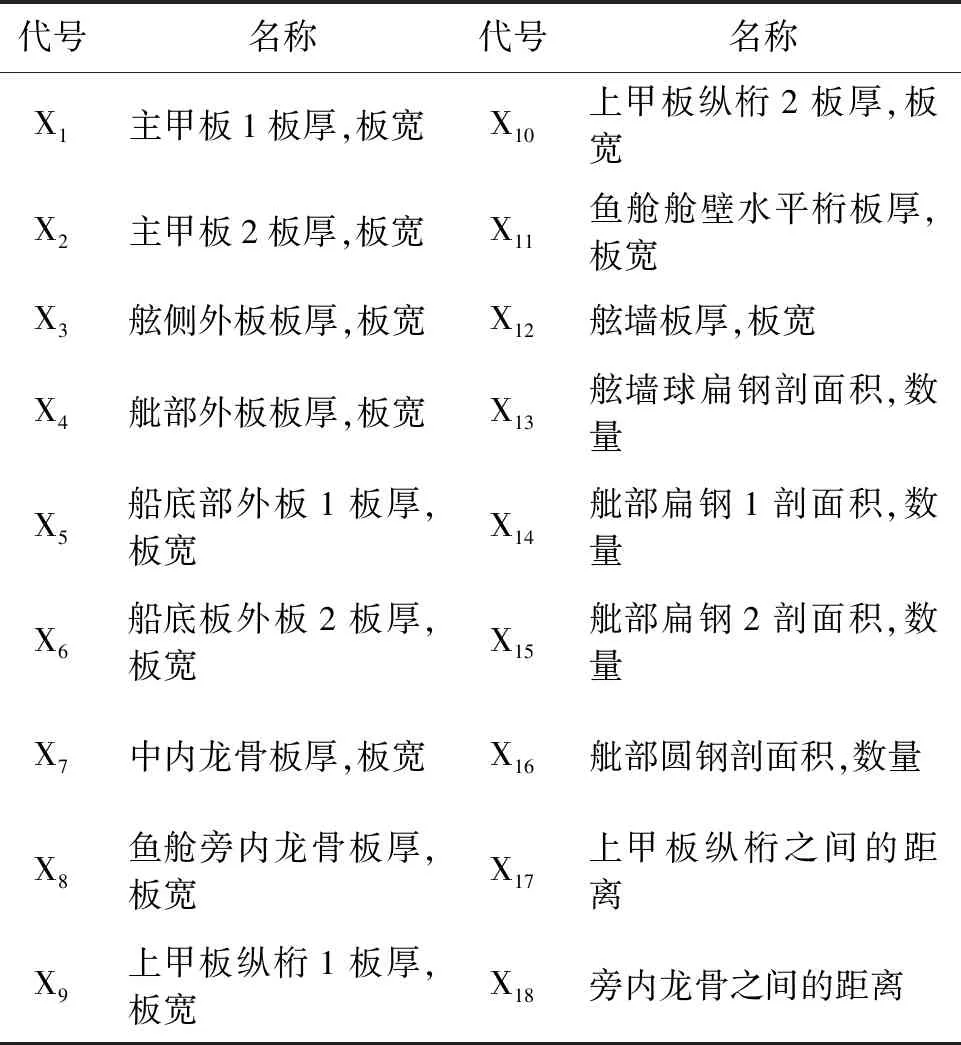
表2 中横剖面纵向构件设计变量代号及名称

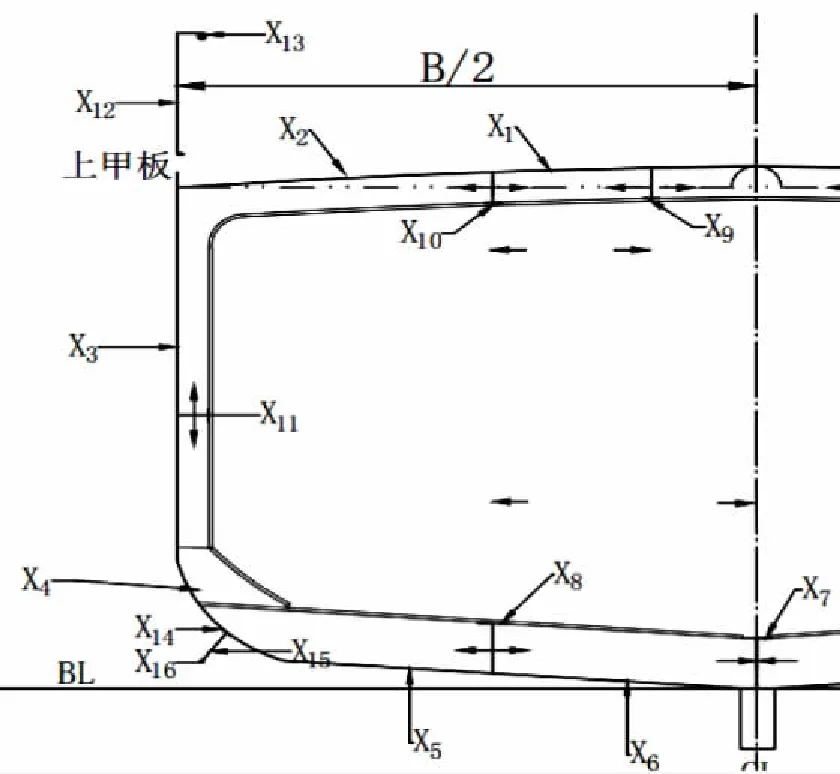
图2 中横剖面设计变量示意图

1.3 初始质量计算

船中第4号鱼舱肋骨间距为500 mm(半个横剖面，包含舭龙骨)。初始质量计算公式：

W=W1+W2

(1)

(2)

(3)

式中：W—舱段初始质量，kg；W1—板材质量，kg;W2—骨材质量，kg;P—钢材密度，P=7.85×103kg/m3;L4—第4号鱼舱舱段长度，L4=4.5 m；ai—对应板材宽度，m；xi—对应板材厚度，mm；bj—对应型材个数；xj—对应型材面积，cm2。将上述数据代入计算得：W=3.38 t。

1.4 约束条件

对渔船中剖面进行结构优化还需要使渔船的总纵强度、局部强度及弯曲强度等得到保证，因此，在《钢质海洋渔船建造规范(2015)》[10]提取8个约束条件，g(X)i为约束条件公式。以下列举四个较为重要的约束条件公式：

(1)中横剖面惯性矩约束条件(根据《钢质海洋渔船建造规范(2015)》[10]选取)。船中横剖面对水平中和轴的剖面模数应满足：

W0=CL2B(Cb+0.7)

(4)

式中：W0—船中横剖面对水平中和轴最小的剖面模数，cm3；C—系数，取值为C=5.77；L—船长，m；B—型宽，m；Cb—方形系数。

船中横剖面对水平中和轴的惯性矩应满足：

I≥3W0L=Imin即g(X)1=I-3W0L≥0

(5)

式中：I—船中横剖面水平中和轴的惯性矩，cm4；Imin—船中横剖面对水平中和轴的最小惯性矩，cm4;W0—船中横剖面对水平中和轴最小的剖面模数，cm3；L—船长,m。

(2)应力约束条件(根据《钢质海洋渔船建造规范(2015)》[10])：

(6)

式中：Imid—该组设计变量所决定的中横剖面惯性矩，cm4；

(7)

式中：σ—横剖面上最大的正应力值，N/mm2，具体求解方法如式(6)所示；许用弯曲应力[σ]=224.36 N/mm2。

(8)

式中：M—弯矩分布系数；I—中横剖面惯性矩，cm4；Z—中和轴到强力甲板边线的垂直距离加上纵向构件的高度，mm；N—静水切力，N；A—剖面面积，cm2。

(9)

式中：τ—横剖面内各构件的剪应力值，N/mm2；许用剪应力[τ]=141.03 N/mm2。

1.5 目标函数建立

本文采用高斯变异算法对蚁群算法进行改进，适用于解决无约束目标函数，因此将有约束的目标函数f(X)应用罚函数法，把约束条件函数g(X)作为罚函数项加入f(X)目标函数中，转换为无约束的目标函数φ(X)：

(10)

(11)

式中：f(X)—有约束的目标函数；g(X)i—约束条件函数，Cp—罚函数中的罚因子，本文取值为0.05;P—钢材密度，P=7.85×103kg/m3；ai—对应板材宽度,m；xi—对应板材厚度,mm；bj—对应型材个数；xj—对应型材面积，cm2。

2 改进蚁群算法

2.1 蚁群算法的基本模型

1992年意大利学者通过模拟自然界中蚂蚁集体寻找食物而得出最短路径的行为中提出了蚁群算法[20]。蚁群算法被乔东平等[15]称为是一种群体智能仿生启发式算法。蚁群算法中人工蚂蚁模仿真实蚂蚁的自然行为，人工蚂蚁之间通过路径上残留的信息素进行交流，并由蚁群完成对陌生路径进行探索并寻找出最短路径。

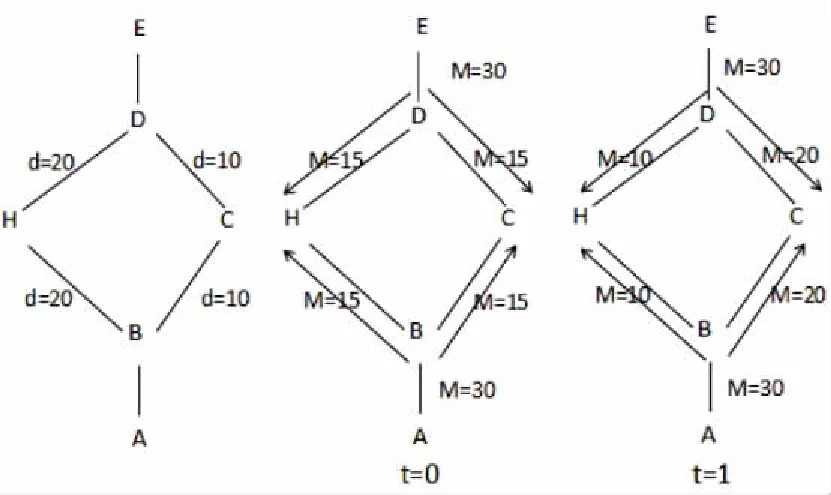
图3 蚁群算法示意图

如图3所示，开始对路径搜索时每个路径被蚂蚁选择概率相同，经过一个单位时间后，由于BCD的长度是BHD的1/2，且假设每只蚂蚁在路径上释放的信息素等量，则BCD路径上的信息素浓度将是BHD路径上的两倍。随着时间的推移，蚂蚁将会以越来越大的概率选择BCD，直至最终完全选择BCD路径，从而找到最优的觅食路径。

对适用于渔船中剖面结构优化设计的蚁群算法基础数学模型进行分析。

(1)初始时刻人工蚂蚁将以任意一构件为起始点随机选择访问下一构件，且每个构件只会被选择一次，最终回到初始构件，并在最后所有路径中选择出最短路径。人工蚂蚁在寻找最优路径中将依据路径上的信息素及期望信息进行转移概率计算[17]，如式(10)：

(12)

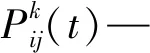
(2)当蚂蚁在游历过所有构件后需要为下次迭代提供有效信息，因此，需要对上次所残留信息进行更新处理，按照式(13)[17]进行更新。

(13)

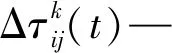
2.2 蚁群算法的改进

所需进行的钢质海洋渔船中剖面结构优化问题是离散优化问题，需要对上述算法进行相对应的改进。文中的设计变量之间的路径距离即是应用单位长度质量等真实参数代替所虚设的距离dij。对蚁群算法改进部分主要体现在蚂蚁选择新路径时，采用高斯变异算法对蚁群算法中的重点区域进行局部搜索。各个蚂蚁对高斯函数的中值和标准差进行动态调整[18]，将原有变量数应用一个符合正态分布的随机数来替代，从而使搜索路径的多样性得到保证，避免算法早熟收敛。

具体实现高斯变异算法步骤如下：将符合正态分布的随机数q用一些符合均匀分布的随机数ri(i=1,2,3,…,12)进行表示，当随机数q～N(m·s2)时，可求得：

(14)

式中：m—服从正态分布的随机数q的期望；s—服从正态分布的随机数q的方差；ri—符合均匀分布的随机数。

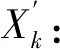
(15)

式中：Lk—随机被选择的构件Xk的左边界；Uk—随机被选择的构件Xk右边界；ri—符合均匀分布的随机数。

3 优化算例

3.1 基于改进蚁群算法的中横剖面结构优化方法计算步骤

采用改进蚁群算法对某43 m流刺网渔船的中横剖面结构进行结构优化设计计算，具体计算步骤如下。

步骤1：输入目标函数公式(10)，对程序进行初始设置；

步骤2：设置初始迭代次数N=0，最大迭代次数为Nmax=50，蚁群规模为K=30，信息素蒸发系数取值为R=0.9，信息素增加强度取值为Q=1，进行输出变量初始化；

步骤3：将m只蚂蚁置于第一级，每只蚂蚁按照相同概率进行转移后，应用高斯变异对重点区域进行局部搜索后产生新的解，直至每只蚂蚁完成对设计变量的搜索后计算本次目标函数值f；

步骤4：按照信息素更新公式(13)朝着信息最大的地方进行转移，得出一条目标函数最小的路径所对应的信息素矩阵元素，N←N+1；

步骤5：若N>Nmax，则停止运行，根据信息素矩阵选择节点，否则转向步骤3；

步骤6：得出最优解及最优函数值。

所设计编程程序的具体计算流程如图4所示。

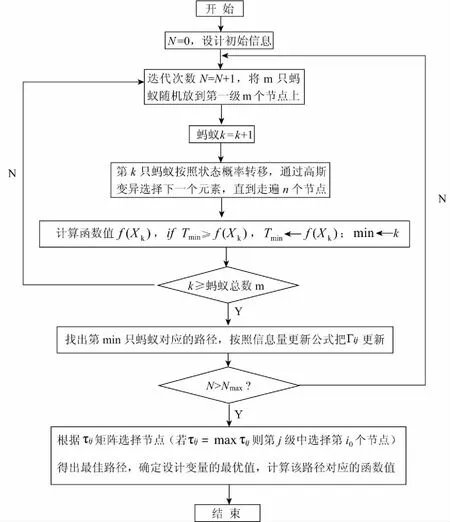
图4 基于改进蚁群算法的中横剖面结构优化计算流程图

3.2 优化计算后结果分析

经过以上步骤迭代过后得出如表3所示结果。中横剖面上主要构件的板厚、剖面积、件间距等均不同程度得到优化。将表3结果代入原中横剖面再次计算其质量，即原始舱段质量为3.38 t，优化后舱段质量为2.96 t，进行结构优化设计的中横剖面舱段结构共减轻质量12.43%。刘宏亮[11]应用人工神经网络对船舶结构轻量化进行研究，最后得到全船质量比未优化前减少11.8%。可见，应用改进后蚁群算法对船舶结构轻量化的效果明显更为适用，所得出的结果更有利于渔船结构轻量化研究。

在对渔船进行中横剖面结构优化计算的过程中，发现蚁群算法较易于改进，能够适应渔船结构优化设计。优化过程中，通过高斯变异算法对重点区域的局部搜索，选择出最为合适的路径变量，从而能够快速寻找到最优解和最优路径。改进后的蚁群算法所具有的高效性及正反馈机制表现很突出，在改动一些参数和对该算法进行修改时也依然能维持原先的功能，同时能够解决渔船结构优化设计这种多元、离散问题，证明了改进后的蚁群算法依旧具有较强的鲁棒性。

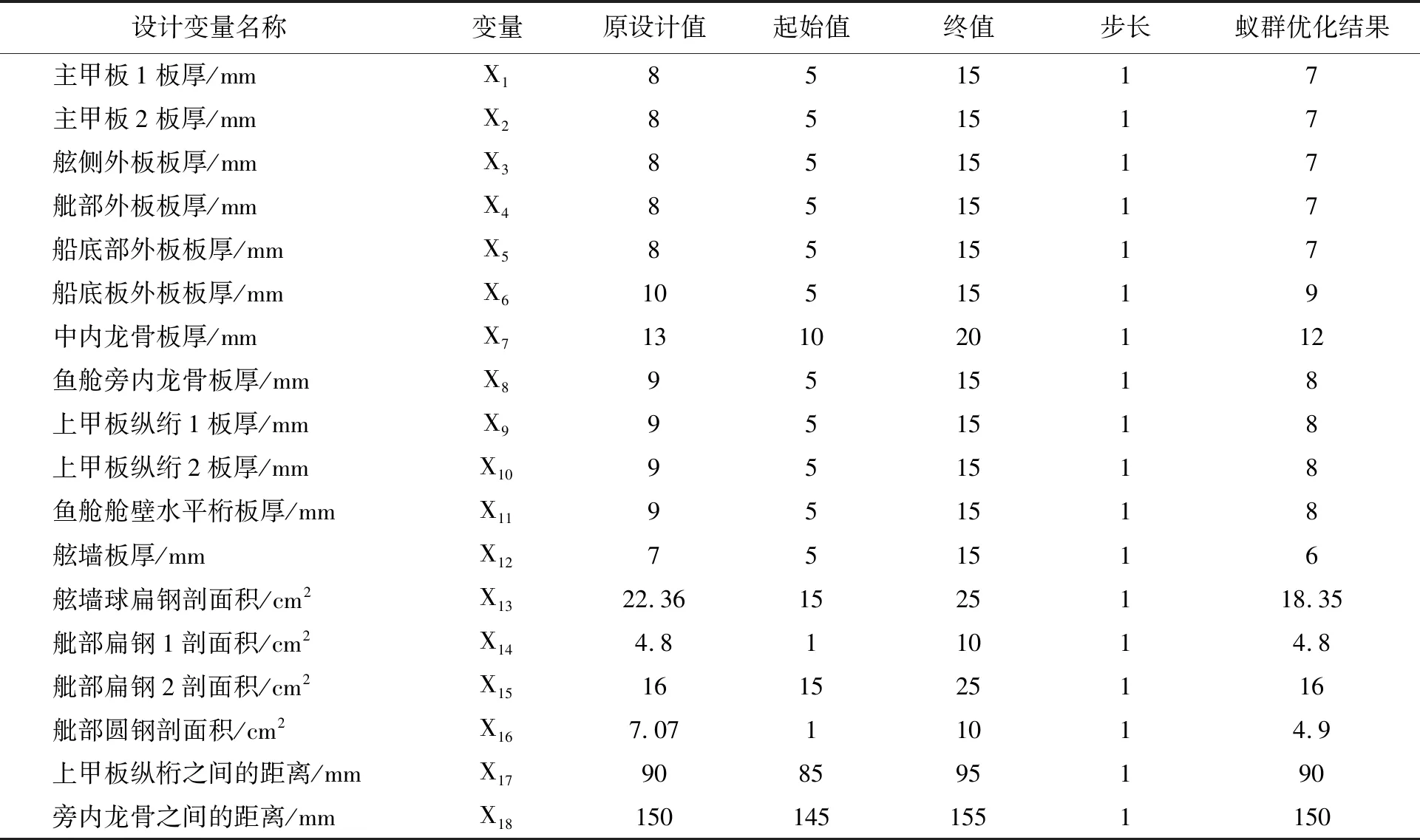
表3 中横剖面结构设计变量优化后的结果

4 结论

根据《钢质海洋渔船建造规范(2015)》建立了钢质海洋渔船中横剖面纵向结构优化设计模型，选取该剖面上主要构件的对应尺寸作为设计变量，对渔船中横剖面结构进行渔船结构轻量化研究。在设计优化算法的过程中，为适应文中所研究的问题，对蚁群算法局部重点搜索采用高斯变异法进行局部搜索，保证搜索路径的多样性，同时避免算法局部收敛，最终得到更为理想的优化结构。改进后的蚁群算法在钢质海洋渔船中横剖面结构优化问题上更为适用且可行，结构轻量化的优化结果更为适用于渔船结构轻量化研究。采用改进蚁群算法对钢质海洋渔船进行结构优化设计，使其质量得到明显减轻。经过船舶结构优化后的渔船可达到节能减排、提高经济性、改善渔船能效水平等效果，符合绿色渔船发展的趋势。

□