基于傅里叶描述子和加权稀疏表示的军事图像分类方法

谢泽奇 张会敏 张善文

(郑州大学西亚斯国际学院 河南 郑州 451150)

0 引 言

军事目标分类作为图像理解的一个基础而且重要的研究课题深受国内外学者的重视，在世界各国国防防御系统中占据十分重要的地位[1-3]。在军事领域，随着军事目标数据的不断增大及军事目标在伪装、遮掩程度的提高，能快速地从大量复杂背景的军事图像集中实现对各类目标进行高精度的图像分类与目标识别，正逐渐成为图像处理、计算机视觉等很多领域的研究热点[4-6]。易崎等[7]提出了一种基于目标特征和支持向量机(SVM)相结合的飞机目标识别算法。该方法首先提取轮廓图像，通过计算目标图像的形状参数的特征矢量构建训练样本，最后训练SVM构建飞机的目标识别模型。该算法在提高识别率的同时，不但减少样本训练时间，而且还降低算法的复杂度。高惠琳[8]采用基于卷积神经网络的深度学习结构对目标进行特征学习，在大量的军事图像分类中取得较高的分类精度。但深度学习中需要较多的经验、人工尝试及技巧，如设置网络层数、每层节点数、节点的激发函数等。李萍等[9]提出通过计算稀疏表示系数实现多姿态的飞机目标识别算法，该算法在出现遮挡和姿态变化时具有较高的识别率。

尽管军事图像分类和识别方法的技术很多，并取得了不错的识别效果，但由于应用背景的复杂性和多变性，使得传统军事图像分类方法难以克服拍摄环境、遮挡、角度等因素的影响，所以传统方法并不能满足实际需要。中心-轮廓距离CCD(Centre-Contour Distance)特征是将轮廓线上的点到形状的几何中心的距离描述成中心角度函数，该方法基本能够重构被描述的目标图像形状[10]。为了能将其转化成一维函数，则需要对这些多值进行选择或者运算处理，但会造成关键信息的丢失而不能实现重构，因此，该算法在描述形状时无法实现唯一性。随着军事图像像素的不断增加，CCD描述形状轮廓的精度及所占带宽也会不断递增，因此其抗噪性弱，且难以克服遮掩、不同姿态、弱特征、视角变化等因素的影响[11-12]。稀疏表示分类SRC(Sparse Representation based Classification)是采用全体训练样本之间的稀疏线性组合来表示一个特定的测试样本[13-14]。本文提出一种改进的傅里叶描述子，在此基础上，与加权SRC相结合[15]，提出一种新的军事图像分类方法。该方法利用了飞机图像的本质特征，能够有效地描述军事图像的形状，在真实的军事图像数据库上验证了该方法的有效性。

1 加权稀疏表示分类方法

设有n个来自k类的训练样本，第i类有ni个样本x1,x2,…,xn，y为测试样本，第i类中ni个样本构成的矩阵表示为Ai=[vi1,vi2,…,vini]∈Rm×ni。则所有样本组成的矩阵A=[A1,A2,…,Ak]∈Rm×n称为过完备字典。加权稀疏表示分类(SRC)算法是通过计算各类训练样本与测试样本的残差大小来实现测试样本的分类，即求解下面的l1范数最小化问题[15]：

(1)

式中:a=[a1,a2,…,an]T为稀疏表示系数，ai(i=1,2,…,n)为第i个样本xi对应的稀疏表示系数，μ>0为调节参数，W为加权矩阵，W由训练样本与测试样本之间的高斯核距离得到。

计算测试样本y在第i类训练样本上的残差：

(2)

式中:Bi为对应第i类训练样本的稀疏表示系数构成的向量。

则测试图像y的类别为y在所有k类训练样本上残差的最小值对应的类别：

(3)

2 军事图像分类方法

军事图像的轮廓包含了军事图像识别的大部分分类信息，是军事图像分割、定位和分类的重要特征。Canny轮廓提取算法是一种简单、实用的轮廓检测方法[11]，具有较好的轮廓检测性能，在复杂图像检测和识别中得到广泛应用。本文在Canny轮廓提取算法的基础上，提出一种基于改进傅里叶描述子与加权SRC算法相结合的军事图像分类方法，该识别方法流程图如图1所示。

图1 军事图像识别流程图

军事图像识别方法的基本步骤描述如下：

1) 军事图像预处理。同一类军事图像的大小、方位、形状和角度之间存在差异，因此在进行军事图像分类前必须对军事图像进行预处理[4-5,7]。首先将拍摄的彩色图像转换成灰度图像来消除对图像分类的干扰。转换公式为：

Y=0.298 9R+0.587 0G+0.114 1B

(4)

式中:R、G和B分别表示彩色图像的红、绿、蓝三个分量，Y表示对应图像的灰度值。

其次，为了降低图像噪声的影响，利用高斯滤波方法对灰度图像进行平滑处理，以便更准确地计算图像的梯度及轮廓幅值，得到的图像为：

f1(x,y)=g(x,y)⊗f(x,y)

(5)

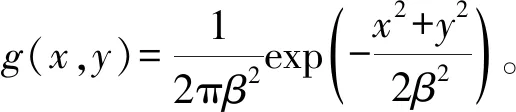
2) 通过偏导数计算幅值和梯度方向。通过在2×2邻域的有限差分计算在x和y两个方向的平滑图像的偏导数：

(6)

3) 确定轮廓点。在水平、竖直、45度和135度的四个轮廓梯度方向搜索各个像素梯度方向的邻接像素。若某个像素点的灰度值与其梯度方向上前后两个像素的灰度值差值较小，则这个像素置为0，即不是轮廓，最后得到轮廓点的坐标集合。

设由步骤1)～3)得到的轮廓点坐标集为{(xi,yi)|i=1,2,…,m}，其中(x1,y1)为轮廓点的始点。

4) 计算轮廓点的中心坐标。计算轮廓点的中心坐标(xc,yc)：

(7)

5) 将直角坐标点转换为极坐标点。以(xc,yc)为极坐标系的极点，将轮廓点的直角坐标点(xi,yi)(i=1,2,…,m)转换为对应的极坐标(ri,θi)(i=1,2,…,m)：

(8)

式中:ri(i=1,2,…,m)为中心轮廓点距离。

6) 按照θi(i=1,2,…,m)的升序对ri进行排序，得到一个中心轮廓点距离序列，记为V=[r1,r2,…,rm]，容易得知V与图像的旋转和平移无关[12]。

7) 对中心轮廓点距离序列进行快速傅里叶变换。由于V与图像的大小和轮廓点序列的起始点有关，为了得到鲁棒的军事图像的分类特征，对V进行快速傅里叶变换。V的K点傅里叶变换为：

(9)

频域变换后的边界序列中F(0)表示直流分量，不能反映不同图像之间形状差异，而较低频率系数能够反映图像形状的主要特征信息，较高频率系数能够反映图像形状的细节信息[15]。

8) 构建傅里叶描述子。根据式(9)构建傅里叶描述子：

(10)

式中：|·|表示傅里叶频谱。

9) 计算高斯核距离。根据式(10)计算每幅测试图像与每幅训练图像的傅里叶描述子之间的高斯核距离。

10) 加权SRC。利用训练集图像的傅里叶描述子构建如式(1)的加权SRC的l1范数最小化问题，求解稀疏表示系数。

11) 分类。计算每一类军事图像的残差，则最小残差对应的类别即为测试图像的类别。

容易证明，FV与图像的缩放和轮廓点集中的起始点无关，而且与图像的大小、旋转、平移和轮廓的起始点无关，所以利用傅里叶描述子对军事图像进行分类方法具有鲁棒性。

3 实验结果与分析

在MATLAB 2010环境下进行军事图像分类实验，实验硬件平台为英特尔双核T6600处理器、主频2.2 GHz和2 GB DDR3内存。为了验证本文算法的有效性，将本文提出的方法与文献[7]、文献[8]和文献[9]提出的军事图像分类算法进行对比。本文SR算法的求解最小化l1范数采用MATLAB的K-SVD字典学习的工具包和求解优化问题的SPGL1工具包。选择10类军事图像组成一个数据库，包括军用汽车、坦克、装甲车、导弹装置、火炮、战斗机、建筑物、队伍、丛林和田野。每类包含图像100幅，共1 000幅图像。图2给出该数据库中的部分军事图像示例图像。采用五-折交叉验证法进行实验，即将图像集中每类图像随机划分为5等分，每等分有20幅图像。在每次实验中，由每类中的1等分共200幅图像作为测试图像，其余的800幅作为训练集，进行图像分类实验。由此可以得到5个实验结果，将其平均值作为这次划分的实验结果。进行50次五-折交叉验证法实验，计算50次实验结果的平均值，为最后的军事图像的分类结果。

(a) 六类军事图像

(b) 不同姿态下的18幅军事飞机图像图2 军事图像实例

首先将每幅图像缩放大小为256×256像素的图像，然后转换为灰度图像，采用Canny算法提取各图像的轮廓，计算中心-轮廓距离序列，再提取该序列的傅里叶描述子，如图3所示。

(a) 灰度图像 (b) 轮廓图像

(c) 中心-轮廓距离 (d) 傅里叶描述子图3 两幅军事灰度图像及其轮廓图像、中心-轮廓 距离序列和傅里叶描述子

为了表明本文提取的军事图像的傅里叶描述子的鲁棒性，对一幅军事图像进行平移、旋转、缩放后得到的5幅扩展图像，如图4所示。然后分别提取5幅扩展图像的傅里叶描述子与第一幅图像的傅里叶描述子之间的相似度，如表1所示。表1中给出了5幅扩展图像与第一幅图像之间及其中心-轮廓距离序列的相似度。相似度选择为两个矩阵或向量之间的余弦距离。

(a) (b) (c) (d) (e)图4 军事图像及其扩展图像

相似度(a)与(b)(a)与(c)(a)与(d)(a)与(e)图像0.862 60.848 30.792 70.694 3中心-轮廓距离0.934 10.889 50.876 80.867 4

由表1可以看出，同类军事图像的傅里叶描述子的相似度比同类图像之间的相似度大。由表1表明，傅里叶描述子对图像的平移、旋转、缩放以及轮廓点系列的起始点具有不变性和较高的鲁棒性。由于基于军事图像形状的傅里叶描述子的能量基本上集中在低频部分，傅里叶变换的高频分量幅度一般较小且易受到噪声干扰，可以使用归一化傅里叶描述子的低频分量来表示军事图像特征的相似差异。在本文实验中取128点快速傅里叶变换进行军事图像识别实验。

计算每幅测试图像与每幅训练图像的傅里叶描述子之间的高斯核距离，构建加权SRC的l1范数最小化问题，求解稀疏表示系数。计算每一类军事图像的残差，则最小残差对应的类别即为测试图像的类别。将本文提出的算法与其他三种方法军事图像分类方法进行比较，表2为四种方法的实验结果。

表2 SVM、CNN、MSRC和本文方法对10类 军事图像的分类结果

从表2可以看出，本文提出的方法的识别结果最好。其原因是本文方法提取的傅里叶描述子能够比较准确地描述军事图像的形状特征，而且具有旋转、平移和缩放不变性，且与轮廓点序列中的起始点无关，加权SRC具有较好的分类性能。CNN方法的识别率不高的原因在于训练样本比较少，不能有效地训练CNN模型。

4 结 语

本文针对军事图像分类问题，在传统傅里叶描述子的基础之上，提出了一种基于改进军事图像傅里叶描述子的军事图像识别方法，并利用加权SRC进行图像分类，取得了较高的分类结果。实验结果表明，改进的傅里叶描述子对图像的平移、旋转和缩放能够保持不变，具有较高的形状区分能力。下一步将傅里叶描述子与深度学习相结合来研究大规模复杂背景下的军事图像进行分类方法，以提高军事图像分类率。同时，对分类方法进一步改进，以实现军事图像自动分类识别系统。