任意初态下的迭代学习控制策略

李国军,韩一士,陈东杰,许中石

(浙江警察学院公共基础部,浙江 杭州310053)

1.引言

迭代学习控制(Iterative learning control,简称ILC)适用于在有限区间作重复操作的场合,通过利用上一次的控制输入和输出误差来产生当前次的控制输入,以便改进输出效果,经过多次迭代以后,系统能够实现完全无误差跟踪[1-2].由于设计简单,在线计算量小并且具有动态特性,所以ILC被应用于工业机器人控制,化工过程控制等场合.

有限时间控制(Finite time control,简称FTC)方法虽然能够在有限时间内让跟踪误差趋于零,但它不能抑制确定性扰动.ILC通过多次迭代学习以后,能够完全抑制时间轴上的确定性扰动.

应用ILC方法时,要求每次的初始定位误差必须等于零或者某个固定值,但这在实际中不可能做到,因此这种严格的要求限制了ILC的应用,也决定着在整个控制过程中不可能做到完全无误差跟踪.实际应用时只能做到在某个指定区间实现实际完全跟踪(Practical complete tracking,简称PCT).在PCT情形下,放松了对初始定位条件的限制,而且PCT允许每次迭代时初始状态各不相同.

为了实现PCT,很多学者做了大量有益的工作[3−23].目前的解决方法主要分为两类,一类是压缩映射方法,另一类是Lyapunov-like方法.在压缩映射方法研究过程中,文[5]讨论了初始定位误差对于系统跟踪性能的影响.通过对系统鲁棒性的分析,作者认为跟踪误差收敛至初始状态误差的某个邻域,而且该邻域的半径和初始定位的误差大小成正比.因此,要想提高跟踪性能,必须提高初始定位的准确度.在固定初态误差下,如果利用脉冲函数,系统能够实现完全跟踪.但在实际中,脉冲函数是不存在的,所以这种完全跟踪也是不可能实现的.文[6]和[7]指出,在固定初态误差(误差不为零)情形下,迭代学习方法能够实现渐近跟踪,让误差渐近收敛于零.文[8-9]提出了一种基于固定初态误差的修正方法,能够在指定区间上实现完全跟踪.对于具有高相对阶的系统.文[10]提出了一种修正方法,在完成对初态误差的修正以后,能够确保系统达到完全跟踪.针对非线性连续系统.文[11]提出了一种针对任意初态的修正方法,但这种方法不能完全修正初始误差,而且只适用于一阶系统.

在收敛性分析过程中,Lyapunov-like方法带来了很大的方便,并且也取得了一些成果[12−26].目前最流行的Lyapunov-like 方法是时变边界层方法和吸引子方法.文[15]引入边界层的概念,由于边界层随着时间单调收敛至零,所以在边界层限定下的控制误差也渐近收敛至零,但此方法只能渐近跟踪,达不到完全跟踪.文[18-20]利用吸引子达到了实际完全跟踪.对于一类离散时变不确定系统,文[21]提出了一种针对任意初态和时变轨迹的离散自适应ILC方法,能够确保系统沿着迭代轴渐近收敛,沿着时间轴在指定区间内逐点收敛.对于可参数化非线性系统,文[22]解决了非一致性轨迹问题,并引入了复合能量函数,给收敛性分析带来了方便.对于带有时变迭代参数的不确定系统,文[23]利用内模控制方法设计参数学习律,确保系统收敛.对于一类反馈可线性化系统,文[24]提出了一种状态反馈ILC,实现了渐近跟踪.但是当控制增益受状态影响时,文中没有提出解决方法.在假定控制增益有上下界和不确定部分可参数化的情形下,文[25]提出了一种带反馈的ILC方法解决了此类问题.

目前,在任意初态下实现实际完全跟踪的算法都是基于Lyapunov-like方法.本文提出了一种基于压缩映射的迭代学习算法,该算法在任意初态下,能够确保系统收敛并且可以实现PCT性能,最后通过一个例子验证了该方法的有效性.

2.问题阐述

考虑下述线性定常系统

其中,t ∈[0,T]是有限时间;k= 1,2,···表示迭代次数;xi,k(t)∈Rn(i= 1或2),yk(t)∈Rr,uk(t)∈Rm,(相应可以简写为xi,k,uk,yk)分别表示第k次迭代的系统状态,控制输入和输出向量.A,B,C是合适维数的系统参数矩阵,并且B右可逆.

设yd(t)(简写为yd)是给定的期望轨迹,设x1,d(t)和x2,d(t)(相应简写为x1,d和x2,d)是给定的期望状态,ek(t)=yd −yk表示第k次输出误差.

假设2.1初始状态x1,k(0)随机,x2,k(0)=x2,d(0),并且状态x1,k(t)和x2,k(t)可测.

本文研究的情形可以对应于实际受控对象处于静止状态(速度误差为零),但有位移误差的情形.

3.控制器设计

本节的任务是设计一个控制算法,使得系统(2.1)能够在指定时间内跟踪上期望轨迹.为此,我们提出下面的控制律.

式中,

其中,h是预先给定的时间常量,为B的右逆.

事实上,控制律中的函数Θ(t)并不唯一,但必须满足下面的性质.

性质3.1对于函数Θ(t),当积分上限满足t ∈[h,T]时,有

证

注3.1这个定理表明,每一个Θ(t)函数,在经过2次积分以后有类似于脉冲函数的作用.在实际中,脉冲函数是不存在的,因此可以用这样一个函数来代替脉冲函数.

4.收敛性分析

这一节着重分析系统(2.1)在应用控制律(3.1)以后的收敛性.在分析之前,先引入下面的定义和引理.

定义4.1函数x(t)的λ范数‖x(t)‖λ按如下方式定义.

其中‖·‖是按以下方式定义的某种范数.如果Z(t)是一个n维向量并且Z(t)=(z1(t),··· ,zn(t))T,那么如果Z(t)是一个矩阵函数并且Z(t) ={zij} ∈Rm×n,那么关于λ范数,有下面的引理.

引理4.1

引理4.2设级数bk满足下列条件,

如果0≤ρ<1,那么

上节提出的控制律(3.1)中,引入了初始修正函数Θ(t),关于初始修正有下面的定理.

乡镇卫生院吊了一夜盐水的英，第二天一早就稀里糊涂地被救护车送到县人民医院。她被带到妇科检查室，一个年轻女医生走进来，叫她脱掉裤子。英开始没有听清楚，女医生又说了一遍，英站在那里不知所措。女医生又大声说了一遍，英明白后开始手忙脚乱地解开裤子，可能因为过于紧张，也可能因为用力太大，裤子的纽扣散了，叮当一声掉落在地板上。英弯腰捡了好几次才捡起，像爱护宝贝一样，将扣子放进了裤兜里。年轻女医生瞧了瞧英，紧接着将戴手套的手伸向她下身。英有些猝不及防，还从来没有人这样看过自己下半身，更不用说用手不停地去触摸。

定理4.1如果初始状态是任意有限值,CBΓ可逆,并且存在一个矩阵Γ满足

那么修正控制律(3.1)能够让系统(2.1)跟踪上期望轨迹,并且在区间t ∈[h,T]上,能够达到一致性跟踪.

证为了方便书写,记

在控制律(3.1)的作用下,当t ∈[0,h],假定轨迹

可实现,即对于下面的系统当x∗2,d(0)=x2,d(0)时,存在控制量u∗d(t) 使得输出为˙y∗d(t).

对于系统(2.1),应用控制律(3.1)可得

在上式两端同时乘以矩阵C,可得

所以当t ∈[0,h]并且‖I −CBΓ‖<1时,根据引理4.2可知,

也就是说,在[0,h]上一致收敛于0.

当t=h时,根据Θ(t)函数的性质有

同理,当t ∈[0,h]时,可得

在上式两端同时乘以矩阵C,可得

同样假设下面的轨迹

可实现,即当系统(2.1)存在任意初始偏差x∗1,d(0)≠ x1,d(0)时,存在控制量u∗d(t) 使得输出为yd∗(t).相应的虚拟系统如下

该系统相应的误差记为e∗k(t)=y∗d(t)−yk(t).

由式(4.11)和(4.12)可得

同理,当‖I −CBΓ‖<1时,根据引理4.2,可得

同样,当t=h时,根据Θ(t)函数的性质有

根据上面的推导结果可知,当t=h并且k →∞时,有yk(t)=yd(t)成立,也就是说,相应地误差为零,系统处于理想状态.

当t ∈(h,T]时,对于任意的xi,k+1(t)−xi,k(t),i=1,2,有

当i=1时,在上式的两端同时乘以矩阵C,并取λ范数,根据引理4.1可得

当λ足够大,并且‖I −CBΓ‖<1时,根据引理4.2可得

当i=2时,用同样的方法能够得到下面的结果，

而且,如果对式(4.17)的两端取导数后再乘以矩阵C,并通过整理可得到下面的2-D模型.

对于上述的2-D模型,如果A,B,C为矩阵,可根据下面的线性矩阵不等式得到Γ(详情见文[26]).

其中,Ar=A,Br=BΓ,Cr=CA,Dr=I −CBΓ,上标T表示转置,P为对称正定阵.

5.数值仿真

考虑如下二阶系统

该系统的作业区间为[0,1],状态修正区间为[0,0.2].系统的跟踪轨迹为系统运行之前初始状态为x1,k(0)=0.5rand(rand产生0到1之间的随机数值),x2,k(0)=0,仿真中迭代次数为15次.

图5.1中,点线代表期望轨迹,虚线,点划线与细实线分别代表第13,14和15次的实际轨迹(图5.2和此相同).从图中可以看出控制律(3.1) 在t= 0.2 时完成状态修正,完全跟踪上期望轨迹.

图5.3和图5.4中,虚线,点划线与细实线分别代表第13,14和15次的实际跟踪误差.

图5.1 期望轨迹yd和实际轨迹yk

图5.2 期望状态轨迹˙yd和实际状态轨迹˙yk

图5.3 各次迭代实际跟踪误差ek(t)

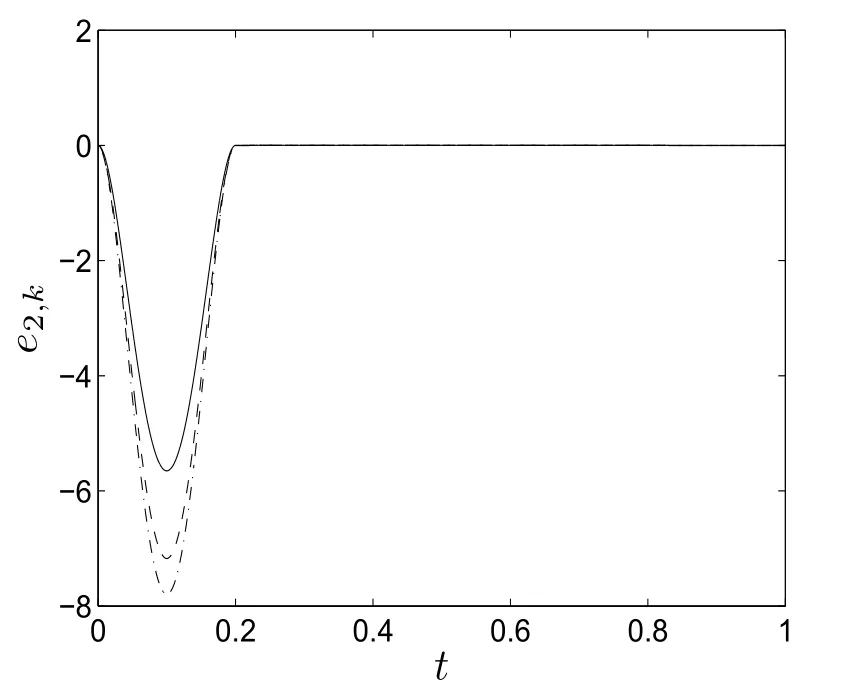
图5.4 各次迭代实际跟踪状态误差˙ek(t)

图5.5 相应的控制量uk(t)

图5.5中,虚线,点划线与细实线分别代表第13,14和15次的实际控制量.从图中可以看出,在修正状态x1,k(t)时,需要很大的控制量.考虑到控制量的限制,一般要求修正时间不能太短.

上面的仿真验证了本文所提算法对于线性定常系统而言,不仅能够完成初始状态误差修正,而且能够在指定区间达到一致性跟踪.

6.结论

本文讨论了线性定常系统存在任意初态误差的迭代学习控制问题,借助压缩映射手段,提出了一种带修正因子的控制策略.在控制过程中,控制算法首先在指定时间内修正初态误差.当修正好所有的状态误差后,系统能够达到无误差跟踪.而且本文也从理论和实践两方面验证了此算法的有效性.