基于点云数据的曲面重建算法比较研究

吴 旭， 卢凌雯， 梁栋栋， 汪晓楚

(1.安徽师范大学 计算机与信息学院，安徽 芜湖 241003；2.安徽师范大学 地理与旅游学院，安徽 芜湖 241003；3.安徽师范大学 地理大数据研究中心，安徽 芜湖 241003；4.苏州市测绘院有限责任公司，江苏 苏州 221008)

在逆向工程、计算机视觉、CAD制图、三维测量技术等众多领域，点云数据处理技术从八十年代起就被广泛应用，且发展至今[1]。随着计算机辅助设计与计算机图形学的发展，越来越多的学者对点云数据的曲面重建技术产生了浓厚的兴趣。从现有研究来看，曲面重构大致可以分为显式曲面重构和隐式曲面重构两类方法[2]。显式曲面重构方法提出较早，需要先将点云参数化，然后再进行曲面重构。它一般不能用单个曲面来直接拟合点云，比如NURBS算法需要先将点云分割成不同区域，然后分别拟合各自的曲面，最后将拟合的各曲面进行拼合得到完整曲面。隐式曲面重构方法利用隐式函数得到逼近点云的等值曲面，相比显式曲面重构方法，隐式曲面重构更适用于重构复杂拓扑形状的曲面，且重构的曲面具有很好的封闭性和完整性。除此之外，刘含波[3]等对曲面重建方法有两种分类方式：根据生成的表面是否经过原始采样点，分为基于插值的表面重建和基于逼近的表面重建；根据重建过程中所依赖的插值点的信息，分为基于全局准则的整体重建和基于局部准则的局部重建。宋大虎等[4]根据现有算法的特点，将曲面重建算法分为隐式曲面算法、参数曲面算法、基于学习的方式和Delaunay三角剖分算法。

本文从点云表面重建方式的角度，把曲面重建分成网格曲面、隐式曲面、参数曲面，其中贪婪投影三角化算法属于网格曲面重建，移动立方体算法以及泊松方程算法属于隐式曲面重建，NURBS算法属于参数曲面重建。

在实际工程中，采用多边形模型如网格方法作为输入输出，无论在数据处理方面，还是在计算机显示方面，都拥有一定的优势[5]。Delaunay三角网的逐点插入法与分治合并法两大方法在19世纪70年代相继被提出。20世纪80年代末，Chew提出了Delaunay Refinement算法[6]，在90年代初，Ruppert改进了Delaunay Refinement算法，使该算法得到的三角形最小角大于20.7度[7]。之后，Rivara、Hitscfeld、Simpson等人进一步扩展和优化，使得最小角的最小值达到30度[8]。基于隐式函数的曲面重构方法可分为局部拟合方法和全局拟合方法。基于局部拟合的隐式函数重构方法出现较早。最早的代表性方法山由Hoppe等[9]人提出，先拟合局部点云的平面，再估算点云的一致性法矢，然后构建有向距离函数，最后提取其零等值面。其中代表性的是移动最小二乘曲面(MLS)方法[10]。和局部拟合方法不同，全局隐式拟合方法利用数学函数同时拟合所有点云数据来重构曲面，径向基函数(RBF)[11]方法是代表性的算法之一。基于参数曲面的重建也是长久以来点云重建的重要手段之一。参数曲面典型的算法有B-splines曲面、NURBS(非均匀有理B样条曲面)[12]以及Bezier曲面。

1 算法描述

1.1 基于贪婪算法的网格曲面重建

贪婪算法常用于将复杂问题简单化，使问题变得更容易解决[13]。贪婪算法的性能影响最大的因素是贪婪三大准则[14]：最近贪婪准则；近邻贪婪准则；定向贪婪准则。

基于贪婪算法的网格曲面重建的核心思想：(1)获得各点的连接关系。将已知点通过法线投影至相应平面，再对投影得到的点作Delauany三角化处理，经软件处理得到各点关系矩阵。(2)生成完整的三角网格曲面。获得各点连接关系后，通过基于Delauany的空间区域增长算法，经初始曲面不断扩张边界，生成结果。(3)形成最后的曲面重建模型。最后按照投影点云的相互关系完成各原始三维点间的拓扑连接获得结果。

1.2 基于移动立方体隐式曲面重建算法

移动立方体算法常用于医学图像可视化三维重建，处理的对象为离散的三维空间规则数据场，主要应用于三维重建的可视化。由于该算法具有步进式的特点，故被称为移动立方体(Marching Cubes)算法[15]。Lorensond等人于1987年提出的Marching Cubes算法是一种流行的从体数据中提取等值面的算法[16]，该算法对每个被处理的体素，以三角面片表示其内部的等值面，它的算法核心思想如下。

(1)三维数据场中构造体素。通过选取立方体中上下两层切片图像形成三维数据场。(2)判断立方体与等值面交点。通过8个顶点函数值与相应等值面阈值的比较，分析生成相应的索引表。(3)获得各顶点处的法向量。通过索引表计算出交点处的坐标，从而获得各处的法向量。(4)曲面重建。由所求三角面片各顶点处的坐标和法向量绘制出等值面，最后实现模型的重构。

1.3 基于泊松方程的隐式曲面重建算法

泊松方程是有着重要应用地位的偏微分方程，应用领域很广，如高动态范围图像的调和映射、图像区域的无缝编辑、流体力学、网格编辑等，其中多重泊松方程已在高效GPU计算得到了很好的应用[17]。基于泊松方程的曲面重构是一种隐式曲面重构方法，与使用较多的有向距离场函数不同。其核心思想如下。

(1)泊松重构采用的是指示函数，即在模型内部为1，外部为0。重构的是修正后的指示函数，其指示函数如公式(1)：

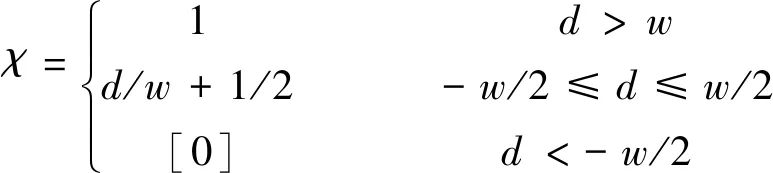
(1)

在此种定义下，可知χ的梯度在距边界w/2内等于有向距离场的梯度d除以w，而在其他地方则恒为0。而有向距离场在某一点的梯度则等于这点对应的曲面最近点的法矢(向内)。如果通过曲面点云中的最近点来近似曲面最近点，则χ的梯度可以由已知定向法矢的曲面点云得到。

(2)在已知函数梯度的情况下重构出函数。记已知的函数梯度为V，定义泛函如公式(2)：

(2)

其中Ω指整个计算域，泛函表示整个计算域上未知函数的梯度场与已知向量场的总误差。令泛函最小，得到经典的泊松方程如下公式(3)：

Δf=Δ*ν(注：边界条件为f|∂Ω=0)

(3)

(3)在离散的情况，使用离散正弦变换代替上面的连续变换，即可得到离散的解，而离散正弦变换可由快速傅立叶得到。最终隐式函数解用Marching-Cube方法转为三角网格。

1.4 基于NURBS技术的曲面重建算法

1975年，有理B样条曲线和曲面被美国Syracuse大学的Verspril研究出来。20世纪80年代后期，Pieg和Tiller经过研究将有理B样条延伸为非均匀有理B样条(Nonuniform Rational B-Spline，NURBS)曲线和曲面。如今NURBS已成为自由曲线和曲面表征的应用较为广泛的技术，国际标准化协会(ISO)已将NURBS的方式作为定义工业产品几何形状的唯一数学方法[18]。NURBS曲面的表达[19]如公式(4)：

(4)

公式4表示k*l次NURBS曲面，其中：di,j(i=0，…，n;j=0，…m)是呈拓扑矩阵阵列的控制点，进而构成一个完整的拥有控制点的网格；Wi,j是与控制点相联系的加权因子；Bi,k(u)为u方向的k阶基函数，Bj,l(v)为v方向的l阶基函数，它们分别由u向和v向的节点矢量决定。利用NURBS进行曲面重建时，其核心思想如下[20]：

(1)针对各切片上的数据，通过计算，将它们换算成带权的型值点；

(2)根据B样条曲线的边界条件及反算公式获得控制点，再把求得的控制点作为v向的型值点，最后沿v向依据B样条曲线的边界条件及反算公式进行反算获得di,j，从而形成整个控制网格。

2 算法实验及分析

2.1 曲面重建前预处理

在测量的过程中，由于仪器本身固有的一些误差以及所测对象所处环境产生的误差，不可避免地对测得的点云数据重建后的曲面产生影响。这些不规则数据难以用统计分析的方法去除，需要进行平滑处理和漏洞修复。在通常不能进行额外扫描的情况下，可以通过对数据重采样来解决这一问题[21]。根据相关研究[22]，移动最小二乘法能通过给定的离散点来近似估计其中的未知点，然后连接这些离散点来获取整个曲面。它不仅保证了原始样本不变，而且用相对少量的空洞边缘的样本就能填补空洞。因此，本文在点云数据曲面重建前，利用移动最小二乘法数据作为平滑处理及漏洞修复技术进行预处理，进一步增强曲面重建的效果。

2.2 四种不同算法的实验结果比较与分析

在逆向工程中，精度体现着逆向生成的模型和现实世界实物之间差距的程度，曲面拟合精度则体现了拟合得到的曲面模型和实物之间的偏差，通常通过实物上的原始点到模型表面的偏差距离来表示[23-26]。曲面拟合精度对曲面重建过程的误差控制、重建方法优劣的衡量有着重要的指导意义[18]。重建算法的评价体系国内外还没有很好的标准。本文主要利用兔子点云数据、建筑物点云数据进行实验，通过从算法本身的时间复杂度、空间复杂度以及重建后的曲面拟合精度等三个方面进行各算法间的比较分析，从而得出研究结果。

本文的所有算法实验都是基于PCL点云库完成的，算法所用的计算机编程语言为C++，计算机的具体配置为Core i3处理器、4G内存以及windows7操作系统。图1为兔子点云数据及建筑物点云重建的实验结果，表1、表2为实验结果分析的数据。

图1 重建结果比较

(图中从左到右对应的组图分别为原始数据点云、贪婪三角化重建结果、移动立方体重建结果、泊松方程重建结果、NURBS重建结果)

从图1可以看出，基于NURBS点云重建与基于贪婪投影三角化点云重建的曲面失真度小，效果较好，基于移动立方体的点云重建与基于泊松方程点云重建的效果次之。从表1四种算法的时间复杂度及空间复杂度可以看出，基于贪婪投影与基于NURBS所用的时间复杂度及空间复杂度较小，基于移动立方体与基于泊松方程的时间复杂度及空间复杂度较大。从表2四种算法重建后精度评价可以看出，两种不同类型的数据，四种算法针对兔子点云重建的误差较小，对建筑物点云重建的误差较大。从兔子点云数据重建中可以看出，基于贪婪投影与基于NURBS重建后的误差较小，基于移动立方体与基于泊松方程重建后的误差较大。从建筑物点云数据重建中可以看出，基于NURBS重建的误差最小，基于移动立方体与基于泊松方程重建的误差其次，基于贪婪投影的误差最大。

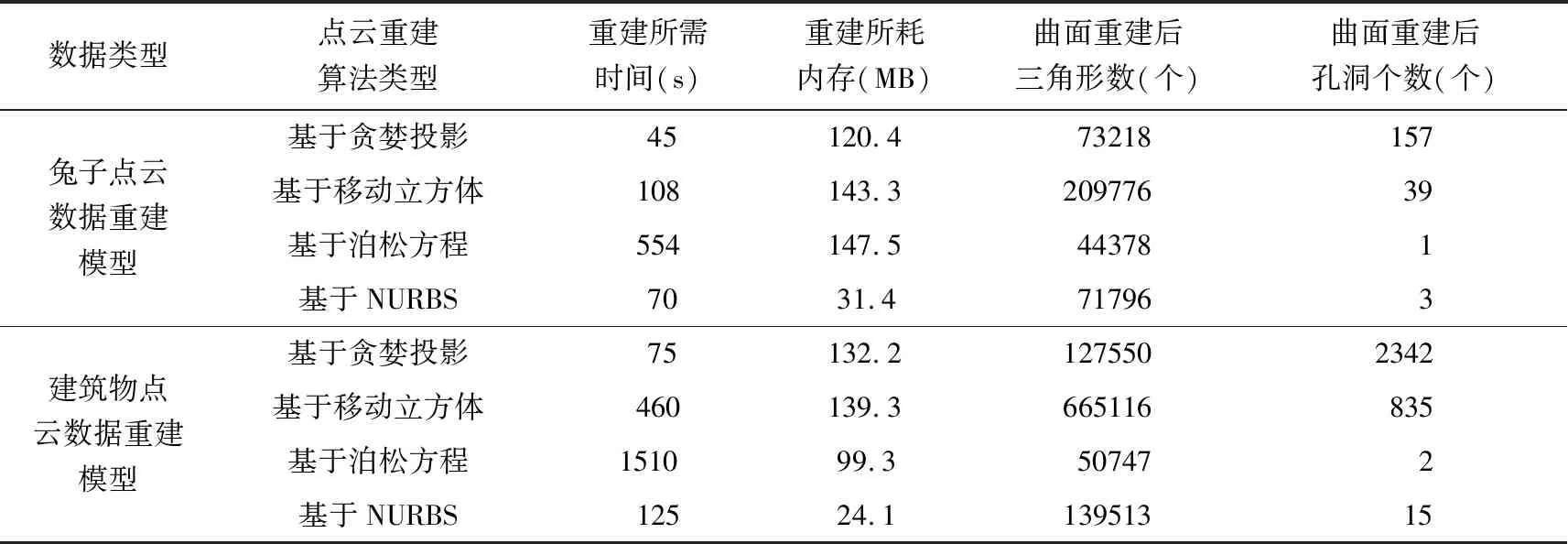
表1 四种算法的时间复杂度及空间复杂度

表2 四种算法重建后精度评价

注：其中Max表示点云与3D曲面模型的最大距离；Mean表示点云与3D曲面模型的平均距离；中误差即所建模型与点云的标准偏差)

综上所述，针对本文涉及的两种类型点云数据中，三种重建方式，基于NURBS参数曲面重建的方式最佳，基于贪婪投影三角化网格曲面重建的方式其次，基于移动立方体与基于泊松方程隐式曲面重建方式的时间复杂度与空间复杂度较大，且重建后的点云模型误差也较大。

3 结束语

本文针对两种不同类型的数据，从点云曲面重建三种方式中，比较了四种不同算法的优劣程度。为了进行点云重建各种算法的比较，提出了通过算法的时间复杂度与空间复杂度以及重建后的精度评价来衡量各算法的优劣。其中重建后的精度评价用点云与3D曲面模型的最大距离、点云与3D曲面模型的平均距离以及所建模型与点云的标准偏差即中误差来表示。实验结果表明，参数曲面重建方式较好，网格曲面重建及隐式曲面重建其次。本研究可以为曲面重建方式的选择提供一定的参考。