奇摄动拟线性边值问题的高阶近似解
孔伟应, 陈怀军, 娄正来
(安徽师范大学 数学与统计学院,安徽 芜湖 241000)
研究奇摄动边值问题,需要在构造形式近似的基础上证明解的存在性[1-7]。1996年,De Jager和江福汝[8]把Harten不动点定理应用到奇摄动拟线性常微分方程初值问题的研究中,随后刘树德等[9]用改进的方法研究了与文[8]相应的边值问题,得到解的零次近似并证明了解的存在性。本文进一步研究奇摄动拟线性边值问题的高阶近似,并应用如下改进的不动点定理。
引理[8](Harten不动点定理) 设(N,‖·‖1)是赋范线性空间,(B,‖·‖)是Banach空间,F是N到B的非线性映射,F[0]=0,且F可分解为
F[p]=L[p]+Ψ[p],p∈N,
其中L是F在p=0的线性化算子,L和Ψ满足条件:
(i)L是双射,L-1连续,即存在常数l>0使
‖L-1[q]‖1∀q∈B;
‖Ψ[p2]-Ψ[p1]‖m(ρ)‖p2-p1‖1, ∀p1,p2∈ΩN(ρ),
其中ΩN(ρ)={p|p∈N,‖p‖1ρ},m(ρ)当ρ→0时单调减少,且
记ρ0=sup {0ρ则对满足‖χ‖的任意χ∈B,存在p∈N,使得F[p]=χ,且
‖p‖1ρ0。
1 形式近似解的构造
考虑奇摄动拟线性边值问题
εy″+f(t,y)y′+g(t,y)=0, 0 (1) y(0,ε)=A,y(1,ε)=B, (2) 其中ε>0为小参数,A,B为常数。 章国华和Howes[10]利用微分不等式理论研究了此问题,在退化问题 f(t,u)u′+g(t,u)=0,u(1)=B 有解uR(t),f,g在[0,1]×R上连续可微且存在k>0使得f(t,y)≥k的主要假设下,推出问题(1),(2)在区间[0,1]上存在一个解y=y(t,ε)且满足如下估计 |y(t,ε)-uR(t)| 其中c>0为常数。在证明了解的存在性的同时也给出问题的精确解与退化解之间的一个估计,但未能构造出满足边界层性质的近似解。 本文我们结合运用合成展开法和Harten不动点定理进行研究。先利用合成展开法构造形式近似解,然后利用不动点定理证明解的存在性,并给出满足边界层性质的近似解,使得它与精确解之间的渐近估计可达到任意O(εn)阶近似。所做工作推广了文[2]及近期相关文献的结果。作假设如下 [H1]f,g∈C([0,1]×R); [H2]退化问题 f(t,u)u′+g(t,u)=0,u(1)=B 在[0,1]上有一个解u0(t),且在[0,1]上f(t,u0(t))>0; [H3]存在k>0,使对介于A和u0(0)之间的任意y,有f(0,y)≥k。 我们先用合成展开法来寻求(1),(2)的形如 y(t,ε)=U(t,ε)+V(ξ,ε) 的渐近解,其中U和V分别称为问题的外部解和边界层校正项,当ε→0时具有渐近级数展开式 vj(+)(+)=0。 (3) (4) 其中 比较(4)式两边关于ε的同次幂系数得到 (5) 及 (6) 其中Fj-1(t)是由u0,u1,…,uj-1逐次确定的已知函数。 此外,由U(1,ε)=B得 u0(1)=B, (7) uj(1)=0,j≥1, (8) 由假设[H2]知,问题(5),(7)在[0,1]上有一个解u0(t),而对每个j≥1,(6),(8)中相应的线性初值问题在[0,1]上均有唯一解uj(t)(j≥1)。 或 (9) f(ξε,U+V)=f(0,u0(0)+v0)+ft(0,u0(0)+v0)ξε fy(ξε,U+θ1V)=fy(0,u0(0))+fyt(0,u0(0))ξε gy(ξε,U+θ2V)=gy(0,u0(0))+gyt(0,u0(0))ξε 比较(9)式两边关于ε的同次幂系数得到 (10) 及 (11) 其中Gj-1(ξ)是由v0,v1,…,vj-1逐次确定的已知函数。 同样地,将U(t,ε)+V(ξ,ε)代入y(0,ε)=A得到 v0(0)=A-u0(0) (12) 及 vj(0)=-uj(0),j≥1。 (13) 利用(12),v0(ξ)可隐式地表示为 其中 由假设[H3]知,v0(ξ)在[0,+)上单调减少,且成立 v0(ξ)=O(exp (-kξ))(ξ→+)。 (14) 现将(11)改写为 上式两边对ξ从ξ到+积分,利用(3)得到 再对ξ从0到ξ积分,并利用(13)可得 因为G0(ξ)是由v0确定的已知函数,故对任意的δ:0<δ<1,可取δ0:0<δ0<δ,使 |G0(ξ)|M0exp (-k(1-δ0)ξ)。 于是 |v1(ξ)| 其中为正常数。 继续用同样的方法,可取{δj}:0<δ0<δ1<…<δ,则存在相应的Mj>0,使 |Gj(ξ)|Mjexp (-k(1-δj)ξ), 随之有 |vj+1(ξ)| 因此对任意δ>0总有 |vj(ξ)|O(exp (-k(1-δ)ξ)(ξ→+),j≥1。 (15) 至此我们已构造出问题(1),(2)的形式渐近解 其中每个vj(ξ)具有性质(14)及(15)。 令 (16) 将(16)代入(1),(2)可得 其中 且由(14),(15)可知R(1,ε)当ε→0时为EST。 再令 而φ(t)∈C2[0,1]满足 φ(t)=0,0tt1, 于是有 (17) (18) 现在我们定义N→B的映射F: 其中N={p|p∈C2[0,1],p(0,ε)=p(1,ε)=0},B={q|q∈C[0,1]}其范数分别为 则B是一个Banach空间,而N是B的一个闭线性子空间,故也是一个Banach空间。又F[0]=0,且F在p=0的线性化算子为 因此 +[g(t,w+p)-g(t,w)-pgy(t,w)] 下面来检验引理中的条件(i)和(ii)。注意到L[p]=0的两个线性无关的解可表示为[2] p1(t,ε)=φ(t,ε), 其中φ和ψ当ε→0时具有如下渐近级数展开式 由于当ε>0时 故对∀q∈B,边值问题L[p]=q,p(0,ε)=p(1,ε)=0有唯一解。因此L是双射。又因为 ‖L-1[q]‖1∀q∈B, 引理中的条件(i)成立。 任取p1,p2∈ΩN(ρ)(0<ρ<1),有 +[g(t,w+p2)-g(t,w)-p2gy(t,w)] -[g(t,w+p1)-g(t,w)-p1gy(t,w)] 故存在常数l>0,使 ‖Ψ[p2]-Ψ[p1]‖ ρ0=sup {ρ|0ρ1,m(ρ) 由于(17)的右边是O(εn+1),故从引理推出,对∀χ∈B:‖χ‖=O(εn+1)存在使且 于是得到如下定理: 定理在[H1]-[H3]的假设下,对充分小的ε>0,问题(1),(2)存在解y(t,ε),且当ε→0时在[0,1]上一致地有 注1若把假设条件[H2]更改为:退化问题 f(t,u)u′+g(t,u)=0,u(0)=A 在[0,1]上存在一个解u0(t),且在[0,1]上f(t,u0(t))<0。则得到与定理相应的结论,但由于不满足右边界条件,故边界层出现在右边。 注2若改用微分不等式理论证明解的存在性,则在假设[H1]-[H3]的基础上,在增加假设[2]:存在常数μ>0,使对介于u0(0)与A之间的任意y,gy(0,y)-μ。故本文所提条件相对较弱。





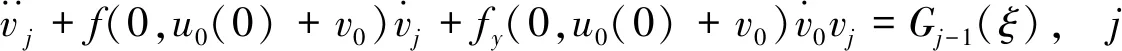






2 证明解的存在性