基于正则的Newton迭代法的内部Neumann反散射问题*
刘立汉,蔡静秋,崔晓英
(重庆师范大学数学科学学院, 重庆 401331)
声波和电磁波反散射问题是数学物理反问题中一个重要的研究领域,它在现代雷达探测、声纳技术、地球物理勘探、医学成像(CT)、无损探测等自然科学和实际工程技术中有着非常广阔的应用前景。而由文献[1]可知,在一些无损探测的工业应用中,利用声波和电磁波探测腔体的结构完整性是非常重要的,这些声波和电磁波是由放置在腔体内的点源和接收器来发射和测量得到的,在这种情况下,点源和测量数据均在散射体内部,因此,我们称这类问题为内部反散射问题。正如文献[2-4]中所提到的,在某些方面,内部反散射问题在物理上比通常的外部反散射问题更加复杂,这是因为所有的散射波都被困在了腔体的内部,它们会被腔体的边界反复反射。文献[2]考虑在Dirichlet边界条件下,利用线性采样法重构腔体的位置、形状及其物理性质;文献[5]考虑在Maxwell方程及其边界条件下,同样利用线性采样法重构腔体的形状、位置及其物理性质;而文献[6]则是将这种方法进一步延拓到阻抗边界条件下来重构腔体的形状、位置及其物理性质,文献[7]是将该方法进一步延伸到混合边界条件下来重构腔体的位置、形状及其物理性质。
然而,本文考虑利用正则的Newton迭代法来求解具有Neumann边界条件的腔体D的内部反散射问题,即从腔体内部某一光滑曲线C上的点源测量数据可以唯一确定Neumann边界条件下腔体的位置、形状及其物理性质。在文献[8]中,Kress和Rundell首先提出了此方法,并且利用该方法求解了Laplace方程的Dirichlet反问题。在文献[9-11]中,将此方法应用于解决腐蚀检测和静电力学中的各种边界值反问题。
1 反散射问题
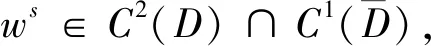
Δws+k2ws=0,x∈D
(1)
(2)
也就是说,总场w=ws+Φ(·,d)满足
(3)
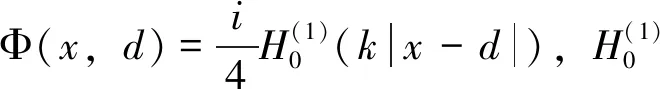
设C是D内的一条闭光滑曲线,对于定点d∈C, 有
ws|C=ws(x,d), ∀x∈C
(4)

证明首先考虑式(1)-(2),用d∈C替代d∈D, 由文献[6]定理2.1的证明过程可知,对于x,d∈C有互反关系
∀x,d∈C
(5)
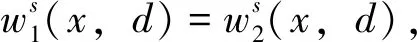
(6)
(7)
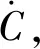
通过互反关系(5), 对于∀d∈C, ∀x∈D0,
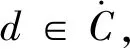
从而由唯一延拓原理知,∀d,x∈D0有
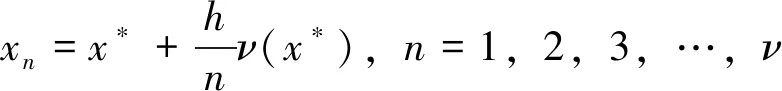
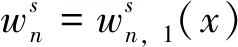
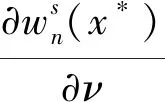
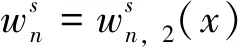
故矛盾,因此D1=D2。
推导出一个等价的积分方程组,即利用单层势能的方法求解反问题。下面用单层势能表示散射场
ws(x)=(Sφ)(x)=
(8)
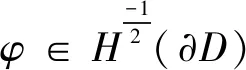
其中,
(9)
(10)
(11)
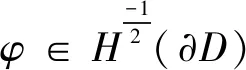
(12)
S0φ=ws(x,d)|c
(13)
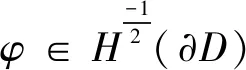
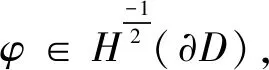
于是由上式及式(4),有∀x∈C,(S0φ)(x)=ws(x,d),即式(13)成立。
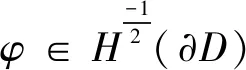
2 反问题的迭代解
在此部分,我们将利用正则的Newton迭代法来求解非线性积分方程(12)、式(13)的未知边界,而边界∂D是非线性的,于是需要线性化系统,且在这个过程中需要计算出关于边界积分算子的Fréchet导数。因此,接下来我们参数化边界及涉及到的积分算子。
2.1 积分方程的参数化
设边界∂D和测量曲线C都是C2类的光滑曲线,将∂D、C表示成参数方程的形式,
∂D={z(t)=(z1(t),z2(t)):t∈[0,2π]};
C={ρ(t)=(ρ1(t),ρ2(t)):t∈[0,2π]}
(14)
对任何的向量a=(a1,a2), 记a⊥=(a2,-a1)表示与其垂直的向量,设
ψ(t)=|z′(t)|φ(z(t))
则积分算子(9)-(11)的参数方程如下(用Ai表示,i=0,1,2)
[A0(z,ψ)](t)=
[A1(z,ψ)](t)=
[A2(z,ψ)](t)=
其中,t∈[0,2π],ψ∈L2[0,2π],z∈L2[0,2π]。
又由式(4)可得到测量数据ω0(ρ(t))=ws(ρ(t),d)和
因此,方程组(12)-(13)变为
A0(z,ψ)=ω0
(15)
(16)
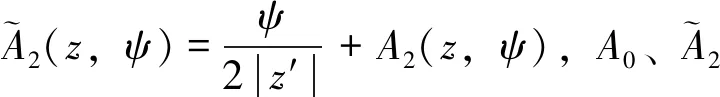
根据文献[14],将它写成如下形式
其中,
M2(t,τ)=
C表示Euler常数。
2.2 正则的Newton迭代法求解反问题
利用正则的Newton迭代法来求解式(15)-(16)的未知边界。
将系统(15)-(16)关于ψ和z完全线性化,有
(17)
ω(z)+ω′(z)ξ
(18)
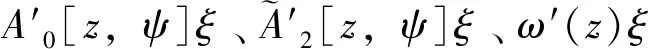
[z(t)-z(τ)]·[ξ(t)-ξ(τ)]ψ(τ)dτ-
[z(t)-z(τ)]ψ(τ)dτ-
[ξ(t)-ξ(τ)]ψ(τ)dτ,
其中,t∈[0,2π]。
不失一般性,设扰动ξ是沿着D的法线指向边界∂D的方向,∂D∈C3使得ξ=q[z′]⊥∈C2[0,2π],标量q∈C2[0,2π], 且精确解ws在∂D上二阶连续可微,对于ψ∈H1[0,2π]和ξ∈C2[0,2π],定义
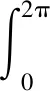
(19)

x∈R2∂D
(20)
由文献[18],可以得到如下引理:
引理1 对于ξ=q[z′]⊥∈C2[0,2π],ψ∈H1[0,2π],标量q∈C2[0,2π],有
(▽U·ν)∘z-
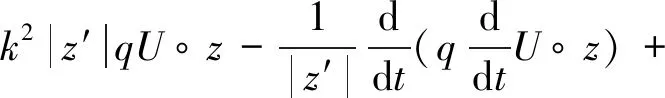
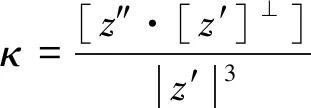
下面说明线性化系统(17)、(18)精确解的单射性。
定理3 令z是精确边界∂D的参数,ψ(t)=|z′|φ∘z,φ满足方程(12)、式(13),若对于标量q, 有ξ=q[z′]⊥∈C2[0,2π]和χ∈L2[0,2π]满足齐次方程组
(21)
(22)
则χ=0和ξ=0。
证明定义
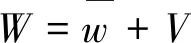
其中
由于
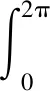
和式(21),有
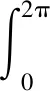

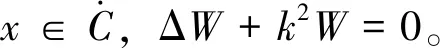
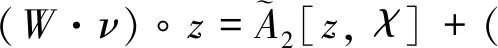
(23)
其中,ν表示∂D向外的单位法向量。由ws是关于密度ψ的单层势能和式(19),有ws=U。又由ψ满足式(15)-(16),则ws满足Neumann边界条件,因此,由引理4及式(23),有
κ|z′|q(▽ws·ν)∘z-k2|z′|qws∘z-
(24)
进一步,由Neumann边界条件式(2)及式(24),有
-ω′(z)ξ-κ|z′|q(▽xΦ(·,d)·ν)∘z
(25)
经计算又有
κ|z′|q(▽xΦ(·,d)·ν)∘z
(26)
联立式(25)-(26),有
(27)
其中,w=ws+Φ(·,d)。于是有
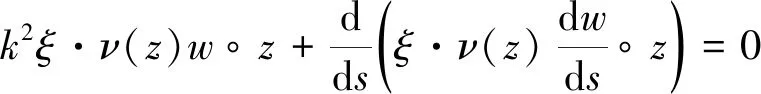
(28)
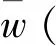
(29)
若ξ·ν≠0,不失一般性,设I={x∈∂D,ξ·ν>0}是非空的,则由式(29),有
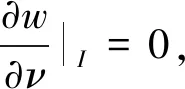
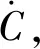
3 数值例子
现在,我们给出三个数值例子来验证我们前面两部分理论结果的正确性。由式(17)-(18)知,求解反问题的边界∂D的算法如下。
第一步:给定初始边界∂D, 即对于z(t),t∈[0,2π],求解非常不适定方程(15),从而得到对应的初始密度ψ。
第二步:由第一步已经有了一个关于z和ψ的近似值,接下来求解线性方程组(17)-(18)的ξ和χ, 从而得到新的边界和密度,即z+ξ和ψ+χ。
第三步:重复第二步,直到满足适当的值才停止。
在以下的例子中,选择k= 5。第一个例子,考虑重构一个半径为0.5的圆,结果见图1。
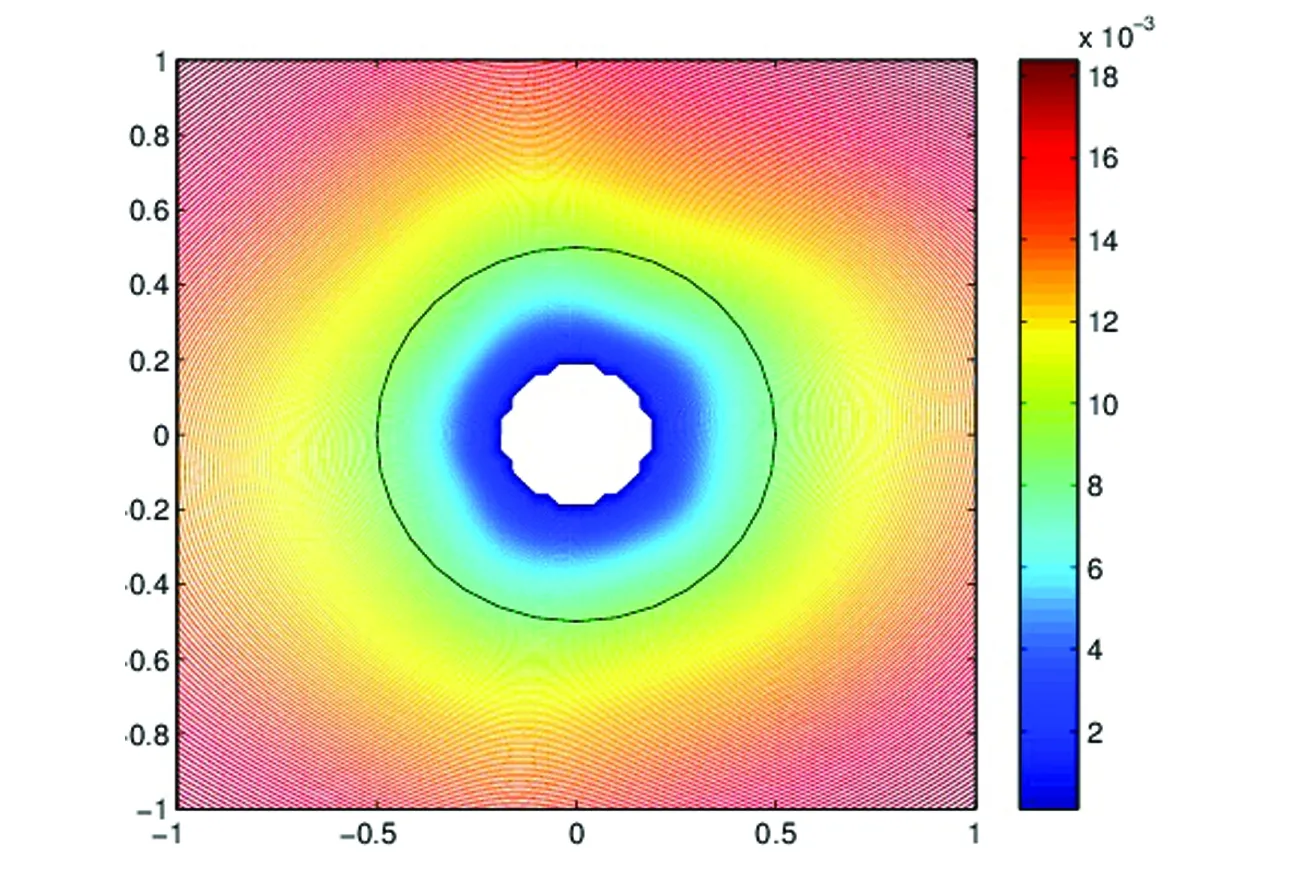
图1 重构半径为0.5的圆Fig.1 Reconstruct a circle of radius 0.5
第二个例子,考虑重构一个长轴长为1,短轴长为0.8的椭圆,结果见图2。
第三个例子,考虑重构一个长为0.8的正方形,结果见图3。
如上的数值例子说明本文提出的正则的Newton迭代法来重构腔体的边界是一种有效可行的算法。
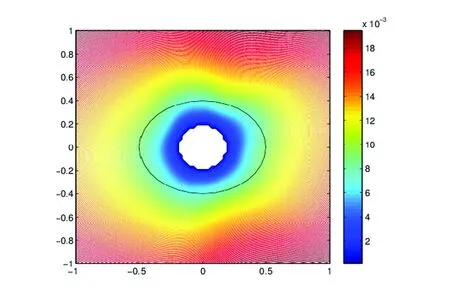
图2 重构长轴为1,短轴为0.8的椭圆Fig.2 Reconstruct an ellipse of x-axis 1,y-axis 0.8
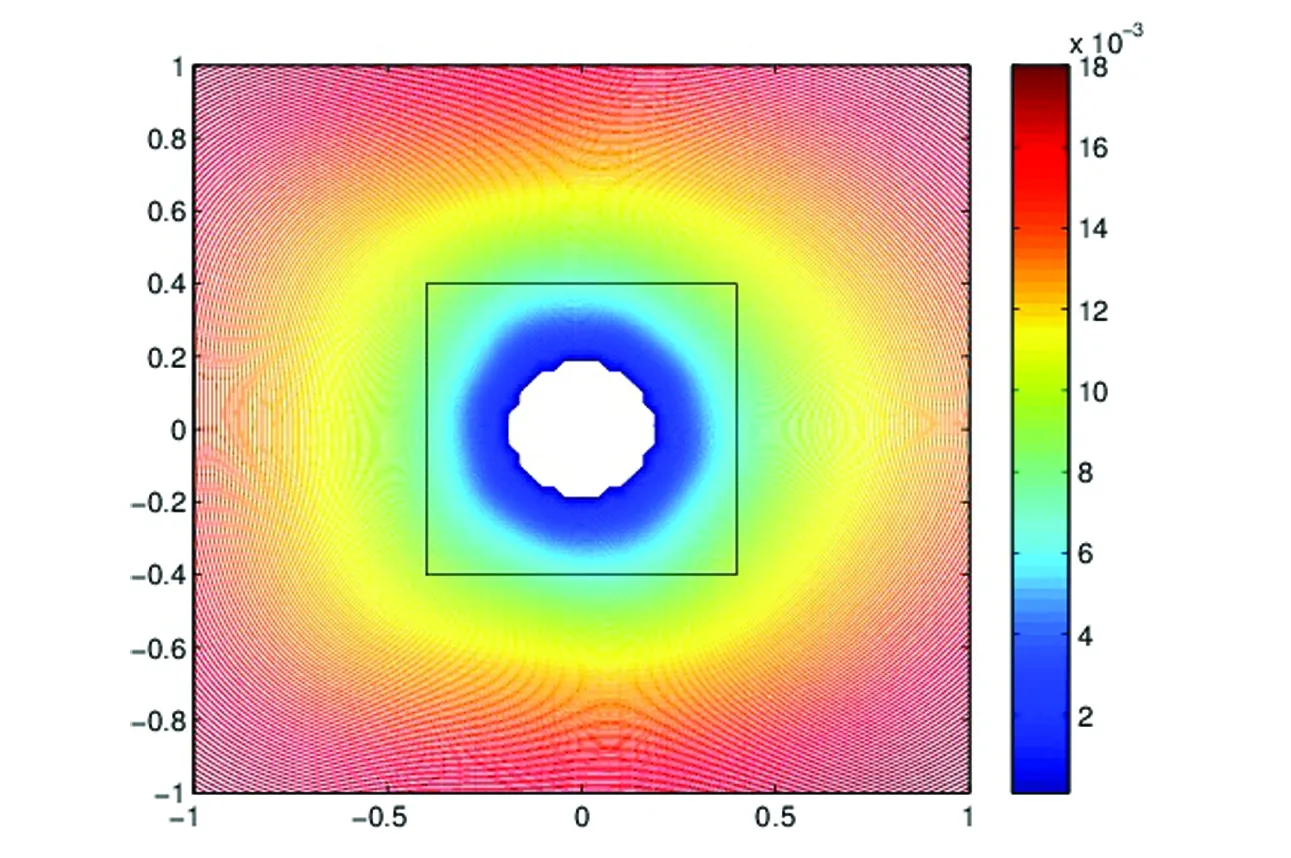
图3 重构长为0.8的正方形Fig.3 Reconstruct a square of length 0.8

