双圈图优雅性猜想*
赵科,李敬文,魏众德,王露露
(兰州交通大学电子与信息工程学院,甘肃 兰州 730070)
图的标号问题是图论的研究方向之一,Chang等[1]在1981年提出了优雅标号的概念。对于给定的图G(p,q),如果存在一个单射f:V(G)→[0,1,2,q],使边标号集合
f(E(G))={f(uv)=(f(u)+f(v))mod(q+1)|
uv∈E(G)}=[1,q]
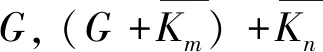
国内外学者主要在研究特殊图的优雅性[8-10],例如圈、路、扇等目前已经证明是优雅的,由于图的总数量庞大且结构多变,而针对一般图的优雅性研究较少。因此,本文结合文献[11]给出的生成非同构简单连通图的算法,设计并实现了一种基于一般图的优雅性判定算法,对16个点之内的双圈图进行优雅性研究,得出了优雅图与非优雅图的分布情况,通过对实验数据进行分析,给出了相关结论和猜想。
1 基本概念和定义
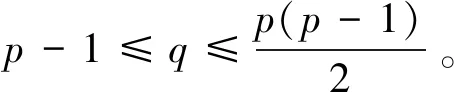
定义1 对于一个给定的简单连通图G=(V,E),如果对每一个顶点v∈V,都对应一个非负整数f(v)(f(v)为顶点v的标号),且满足:
(i)∀v1,v2∈V,如果v1≠v2,则f(v1)≠f(v2);
(ii){f(v)|v∈V}∈{0,1,2,|E|};
(iii)∀e1,e2∈E,如果e1≠e2,则g(e1)≠g(e2),其中g(e)=(f(v1)+f(v2))mod(q+1),e=v1v2。
(iv){g(e)|e∈E}∈{1,2,,|E|};
则称f为G的一个优雅标号(elegant labeling),G称为优雅图(elegant graph)。
定义2 当p≥4且q=p+1时,存在一类(p,q)图,我们称之为双圈图(bicyclic graphs),记为(p,p+1)图。
定义3 ∀m,n≥3,由Cm和Cn仅共用一个顶点形成的(p,q)图,记为C(m,n),其中p=m+n-1,q=m+n。
定义4 对于边数为q的优雅图,满足以下条件:
(i)Min(f(u),f(v))≥0;
(ii)Max(f(u),f(v))≤|E|;
(iii)(f(u)+f(v))mod(q+1)=g(e),且g(e)≠0。
则称边数为q的优雅集合,又称q优雅空间,如表1所示。对于每个g(e),只取一个二元组(m,n),这些二元组集合组成的图都是优雅的。
m的取值范围为{0,1,,q};
n的取值范围可通过如下公式判断取得:
if (g(e)-m≥0)n=g(e)-m;
elsen=g(e)-m+q+1;
在优雅空间中,当m=n时,因每个点的标号不同,故去除;为了避免重复,当m>n时,去除该二元组(m,n)。

表1 q优雅空间Table 1 Elegant space of q
q优雅空间举例:图1是一个(9,10)优雅双圈图,其对应的优雅空间q=10。如表2所示,加粗的二元组是双圈图中每个边标号所对应的顶点标号。
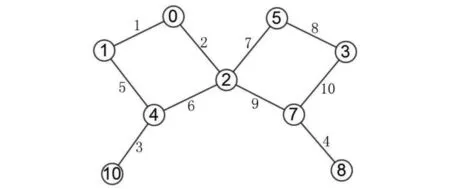
图1 (9,10)图优雅标号Fig.1 The elegant labeling of graph (9,10)
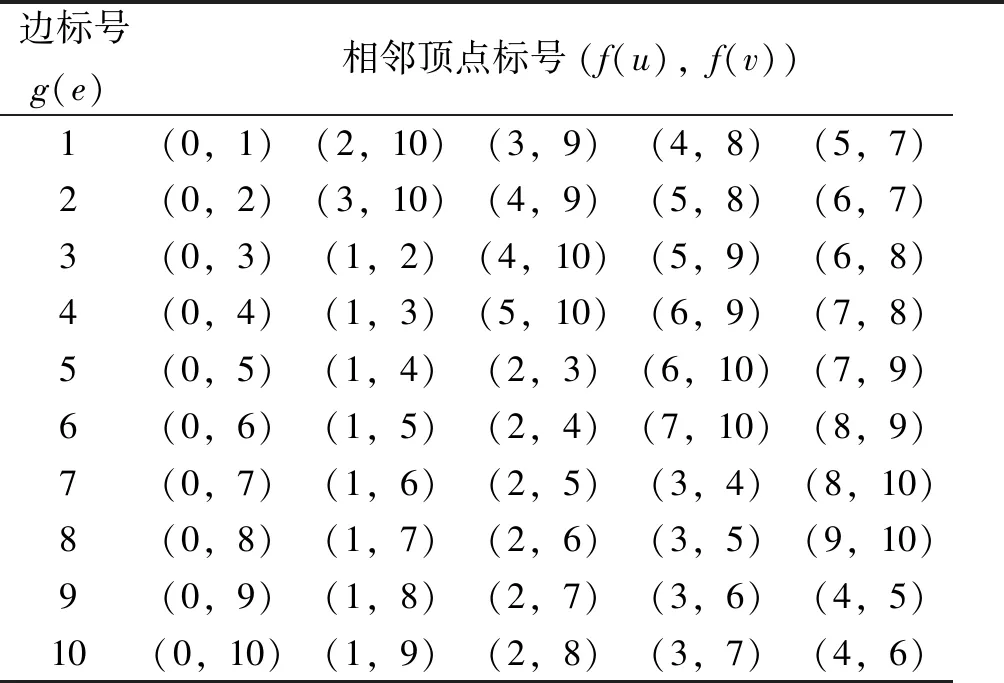
边标号g(e)相邻顶点标号(f(u),f(v))1(0,1)(2,10)(3,9)(4,8)(5,7)2(0,2)(3,10)(4,9)(5,8)(6,7)3(0,3)(1,2)(4,10)(5,9)(6,8)4(0,4)(1,3)(5,10)(6,9)(7,8)5(0,5)(1,4)(2,3)(6,10)(7,9)6(0,6)(1,5)(2,4)(7,10)(8,9)7(0,7)(1,6)(2,5)(3,4)(8,10)8(0,8)(1,7)(2,6)(3,5)(9,10)9(0,9)(1,8)(2,7)(3,6)(4,5)10(0,10)(1,9)(2,8)(3,7)(4,6)
2 解决问题的思路及算法
2.1 解决思路
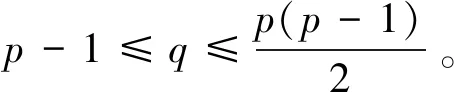
1) 根据(p,q)图的边数q生成图的优雅空间,可以组合成的图G如下:
2)G个图都是优雅图,由连通图与非连通图组成;
3)任意一个连通图若是优雅图,则一定在图G中;若不在其中,则该图一定为非优雅图。
2.2 优雅图判定算法
首先利用文献[11]中的非同构图生成算法,生成顶点数分别为4至16的双圈图文件,并以邻接矩阵形式存储于p_p+1.txt文件中,并计算出各顶点对应图的个数;用文中设计的优雅性判定算法对每个图进行验证。本算法采用剪枝与预判函数相结合的方式,设计的递归回溯算法,基本思想及详细步骤如下。
算法的基本思想是:对于给定的一个双圈图,对应图的邻接矩阵为M(n,n),其中Mii代表图中的各个顶点,Mij=1代表顶点i与顶点j之间存在一条边(i≠j),Mij=0代表顶点i与顶点j之间没有边(i≠j)。对Mii进行优雅标号,标号过程为:1) 从(p+1)优雅空间中从上至下,从左至右遍历二元组(m,n),首先生成边标号为1的一个二元组;2) 判断该二元组是否可用,如果可用,将(m,n)分别标在Mii与Mjj处,且Mij=(m+n)mod(q+1);如果不可用,从左到右寻找下一个二元组,若二元组没有,递归到上一层;3)边标号递增,重复过程1)、2),如果生成边标号为q的二元组,且在矩阵中标记成功,则判断该图是优雅的,算法退出,如果优雅空间已遍历完,算法结束。算法详细步骤:
算法:双圈图优雅性判定算法
Input: 一个图的邻接矩阵M(n,n)
output: 该图是否为优雅图
1.Begin:
2.Calculate the number of edges, generate an Elegant Space;
3.edgeCount∈{1,2,q,q+1}
Set edgeCount=1;
4.DeepSearch (edgeCount)
5.{
6.If (edgeCount=q+1)
7.Success and quit;
8.Select a two tuple(p1,p2);
9.Forp1 0→q
10. if (edgeCount-p1≥0)p2=edgeCount-p1;
11.elsep2=edgeCount-p1+q+1;
12.edgeCount=(p1+p2)%(q+1)
13.Checkp1 andp2 in Martix;
14.Fori1→n
15.if(Miican be use)Mii=p1;
16.Forj1→nandi≠j
17.if (Mjjcan be use &&Mij==1)
18.{
19.Mjj=p2;
20.Mij=edgeCount;
21.edgeCount=edgeCount+1;
22.DeepSearch(edgeCount);
23.}
24.End Forj1→nandi≠j
25.End Fori1→n
26.if (Elegant Space is Finished)
27.This Graph is UnElegant;
28.End
该算法是针对一个特定图对应的邻接矩阵进行标号,如果该图是优雅的,则可以快速得到一个优雅标号,具有较好的时间收敛性;如果该图是非优雅的,则要搜索完整个优雅空间,此时算法具有较高的耗时。利用该算法,可以对本文中所涉及的所有的双圈图进行优雅性验证。
3 算法结果与分析
本文结合文献[11]中的生成所有非同构图的算法,运用文中设计的优雅性判定算法,对顶点数4≤p≤16的所有双圈图进行优雅性验证,统计了双圈图的优雅个数、非优雅个数,及特定(p,p+1)图优雅性验证所运行的时间。本文列举了部分优雅双圈图的标号,标号无规律可循,用传统手工方式较难标出。
算法的运行环境如下:
计算机处理器:Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz
运行内存:64.0 GB
运行的操作系统:Windows 7 64位
算法开发软件:Visio Studio 2013
开发语言:C#
3.1 16个点内所有双圈图优雅个数统计
双圈图优雅个数统计如表3所示,其中第一列为(p,p+1)图,代表顶点数和边数确定的一类双圈图,第二列与第三列分别表示这一类双圈图的优雅图总数与非优雅图总数,第四列为这一类双圈图的总个数,第六列为判断该类双圈图中每个图的优雅性所耗费的时间。
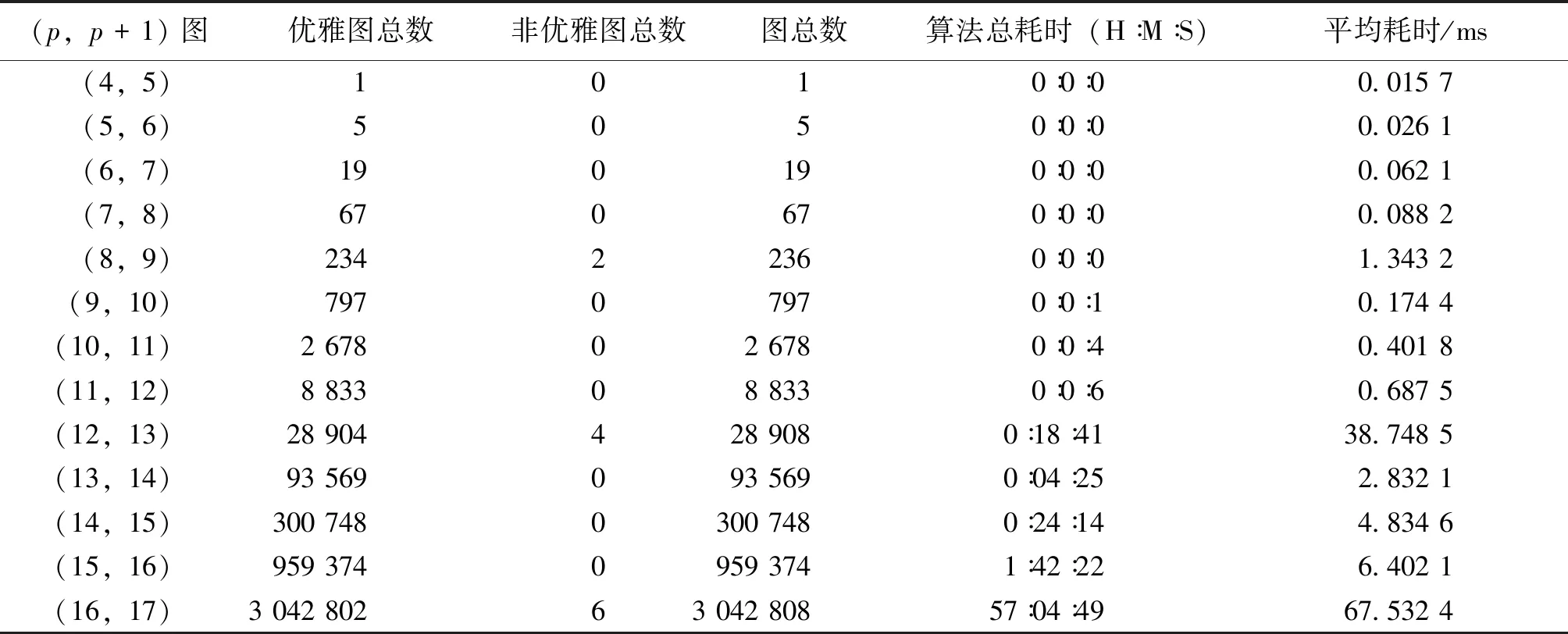
表3 16个点内双圈图的优雅性统计表Table 3 The statistics of the elegant of bicyclic graphs in 16 points
3.2 定理和猜想
定理1 对于(p,p+1)图,当4≤p≤16且p+1≠1(mod 4)时,双圈图(p,p+1)都是优雅的。
证明由算法的正确性及表3可知,定理1成立。
猜想1 对于(p,p+1)图,当p+1≠1(mod 4)时,双圈图(p,p+1)都是优雅的。
定理2 对于(p,p+1)图,当4≤p≤16且p+1=1(mod 4)时,双圈图C(m,n)是非优雅图。
证明由双圈图的定义可知,q=p+1。假设q(mod 4)≡1时,双圈图C(m,n)是优雅图。
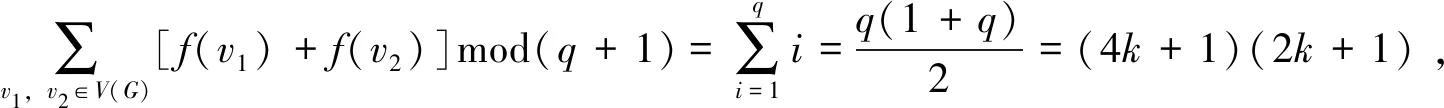
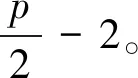
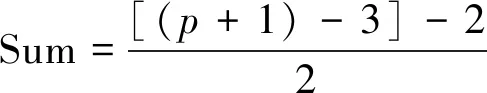
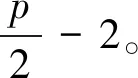
3.3 16个点内所有非优雅双圈图
图2给出16个点内的所有非优雅双圈图,非优雅双圈图图的命名规则如下:在C(m,n)中,m为第一个圈图Cm的点数,n为第二个圈图Cn的点数。
3.4 16个点内部分优雅双圈图
本文列出部分双圈图的优雅标号,且这些双圈图的优雅标号用手工方式较难标出,以便增加算法的真实性和实用性,图的命名规则如下:p_q_number,其中p表示图的顶点数,q表示图的边数,number表示为(p,q)图中列举的第几个优雅图,若只有一个优雅图,则number予以省略。图(12,13)、(13,14)、(14,15)部分优雅图如图3所示,(15,16)、(16,117)部分优雅图见图4,(17,18)、(20,21)、(24,25)、(29,30)部分优雅图见图5。
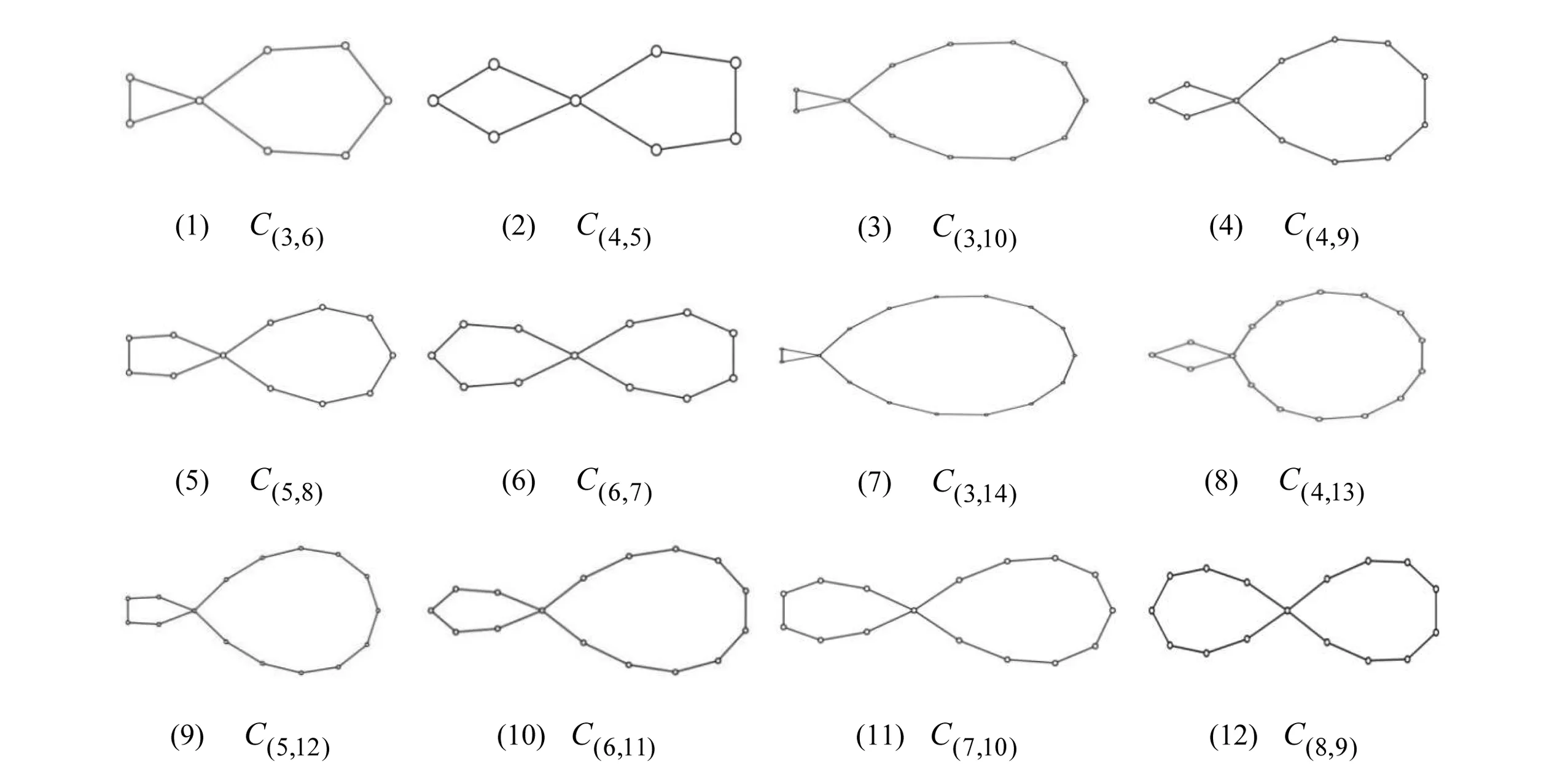
图2 16个点内的所有非优雅双圈图Fig.2 All non-elegant bicyclic graphs in 16 points
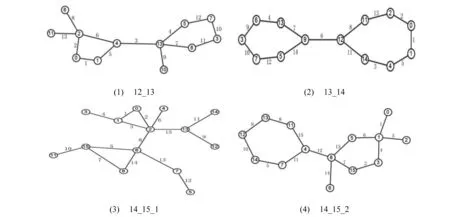
图3 (12,13)、(13,14) 、(14,15)部分优雅图Fig.3 Partly elegant graphs of (12,13)、(13,14)、(14,15)
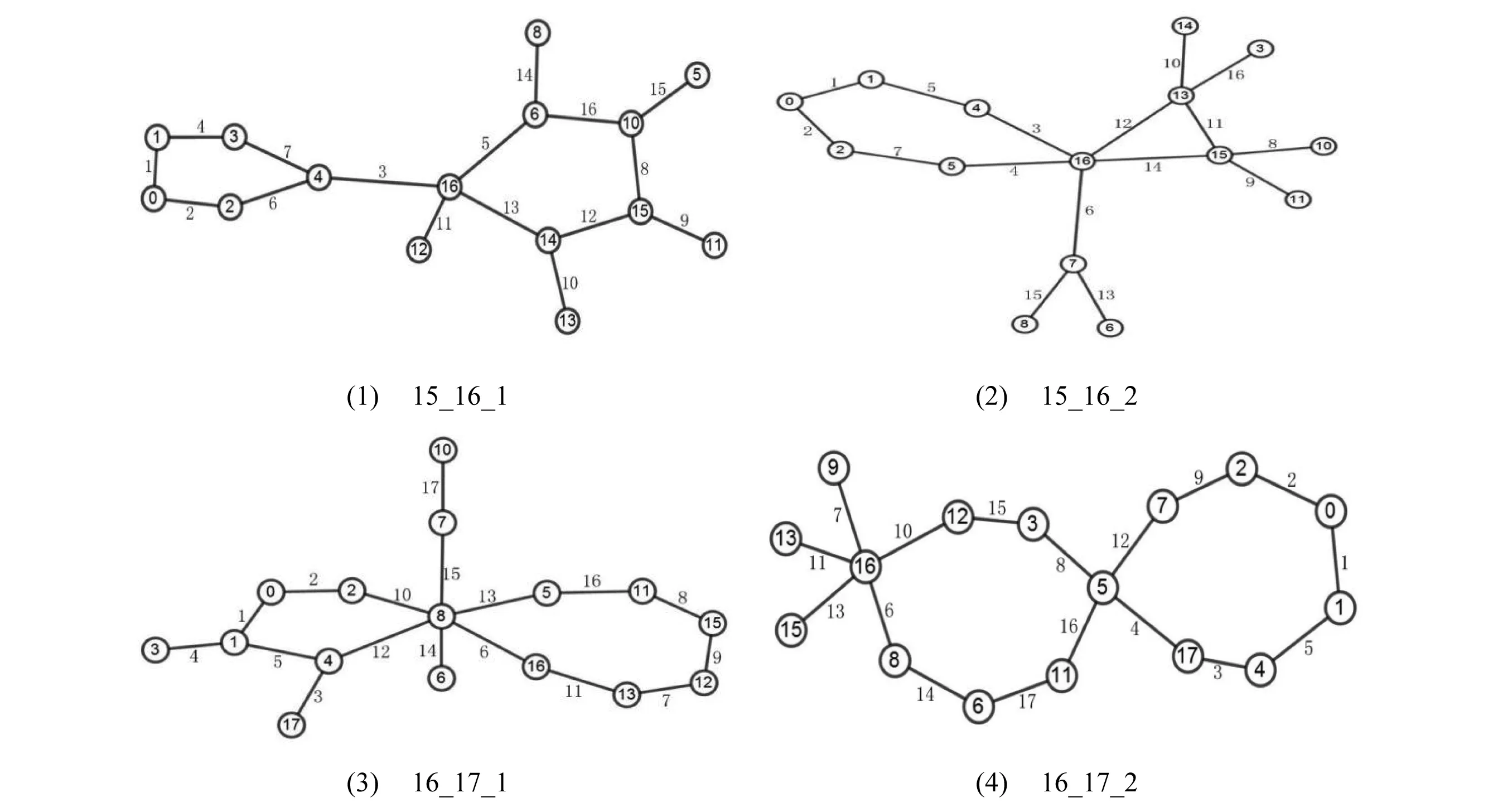
图4 (15,16)、(16,17)部分优雅图Fig.4 Partly elegant graphs of (15,16)、(16,17)
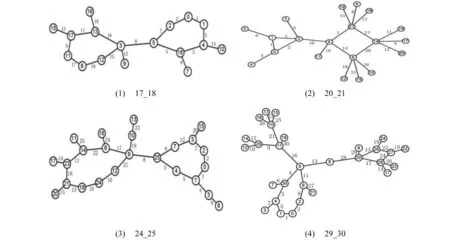
图5 (17,18)、(20,21)、(24,25)、(29,30)部分优雅图Fig.5 Partly elegant graphs of (17,18), (20,21),(24,25), (29,30)
4 结 语
本文给出了一种针对所有图的优雅性验证算法,利用该算法对16个点内的所有双圈图进行优雅性验证,得到其中的优雅图及非优雅图个数。结果表明,16个点内的所有双圈图,除了当(m+n)(mod 4)=1时,图C(m,n)为非优雅图外,其余的双圈图都是优雅的。文中第三节给出相关数据及部分非优雅图,为图标号领域内进一步证明相关猜想提供基础数据支持。随着点数的增加,图集过多导致算法执行效率下降,不能对16个点之后的所有双圈图进行一一验证,故只在第三节列出16个点以上的部分优雅双圈图。在今后对算法进一步优化,以便取得新的突破。
通过对程序结果进行分析,对一个双圈图(p,p+1)是否非优雅做如下断言:当p+1(mod 4)=1且双圈图为C(m,n)时,该双圈图为非优雅图。基于以上实验结果,提出一个公开问题。
问题:随着点数p的增加,双圈图(p,p+1)是否依然满足猜想2?

