电动汽车用PMSM模糊模型预测控制的研究
沈佳烨,吴 雷,黄竞智
(江南大学,无锡 214122)
0 引 言
从2009年起,我国的汽车生产量和新车销售量已处于世界领先,汽车给我国的能源和环境带来了巨大的压力。电动汽车作为一种零排放、无污染的交通工具,具有广阔的发展前景。电动汽车用电动机要求具有过载能力强,转矩响应快,调速范围广,功率密度高,转矩脉动低等特点。永磁同步电机(以下简称PMSM)相较其他电机有体积小,效率高,控制简单等优点,得到了广泛的应用。目前电动汽车用PMSM的控制系统主要有直接转矩控制(以下简称DTC)和矢量控制两种。两种控制方法中DTC技术相较矢量控制技术而言,控制结构简单,受电机参数影响小。但传统的DTC磁链和转矩波动比较大,稳态性能比较差。对此,国内外学者在改进传统DTC方面做了大量研究,如空间矢量调制结合DTC[1],模糊控制结合DTC[2],神经网络结合DTC[3],模型预测控制[4-5]等。应用于驱动领域的MPC又有连续控制集和有限控制集MPC。有限控制集MPC在考虑逆变器可能的开关状态下,以代价函数最小化为目标,选择合适的开关状态,其中代价函数包含转矩、磁链的跟踪误差和定子电流的目标限定,代价函数中各项权重系数的作用是调节该项与其他控制目标之间的重要性,所以正确设计合理的权重系数对于选择合适的电压矢量有重要的意义。文献[6]将模糊逻辑控制加入MPC中,动态地调整代价函数中的权重系数,从而选择最佳开关状态。
传统DTC中,速度控制器采用PID控制器,通过反馈误差来消除误差。但这种控制方法会在闭环系统中产生快速性和超调之间的矛盾。自抗扰控制(以下简称ADRC)针对PID固有的缺点,提出了通过扩张状态观测器(以下简称ESO)来估计系统总扰动,通过跟踪-微分器(以下简称TD)来实现可靠获取微分信号,以安排过渡过程来减少因突变而引起的系统超调,通过非线性状态误差反馈控制(以下简称NLSEF)来改善控制效果这些方面的改进[7-8]。但非线性ADRC参数较多,不易调节,利用模糊控制对参数调节能够良好估计的特点,在ADRC中引入模糊控制,以便参数调节。
本文在模型预测DTC的基础上,加入了模糊逻辑控制,动态地确定权重系数的值,从而选择能最小化电磁转矩和定子磁链误差的电压矢量。此外,在速度环采用模糊一阶ADRC代替传统的PI控制器,能够有效地改善系统的动静态性能,磁链转矩脉动小,速度跟踪快,无超调。
1 PMSM的模糊模型预测控制
1.1 PMSM数学模型
本文以表贴式PMSM为研究对象,忽略铁心损耗,假定PMSM的转子每相气隙磁动势呈正弦分布,则在d,q旋转坐标系下,PMSM的定子电压方程、磁链方程、转矩方程如下:
(1)
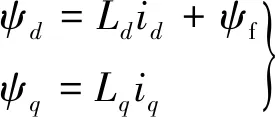
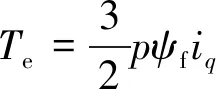
式中:ψd为直轴磁链;Ld为直轴电感;ψf为永磁体磁链;ψq为交轴磁链;Lq为交轴电感;ud为直轴电压;uq为交轴电压;id为直轴电流;iq为交轴电流;ωe为转子电角速度;R为定子电阻;p为极对数。对于表贴式PMSM,有Ld=Lq=L。
1.2 离散时间模型
在离散时间模型中,根据一阶欧拉近似法,可以得到对采样时间T的定子电流导数:
(4)
两相旋转坐标系下,定子电流预测表达式为:
(5)
式中:id(k+1),iq(k+1)为下一时刻的直轴电流值和交轴电流值;id(k),iq(k)为当前时刻的直轴电流值和交轴电流值;电压输入向量ud(k),uq(k)可由下式变换矩阵得到:
式中:[Sa(k),Sb(k),Sc(k)]T为逆变器的开关状态,一共有8种状态:[0,0,0]T、[0,0,1]T,…,[1,1,1]T,对应的空间电压矢量如图1所示。
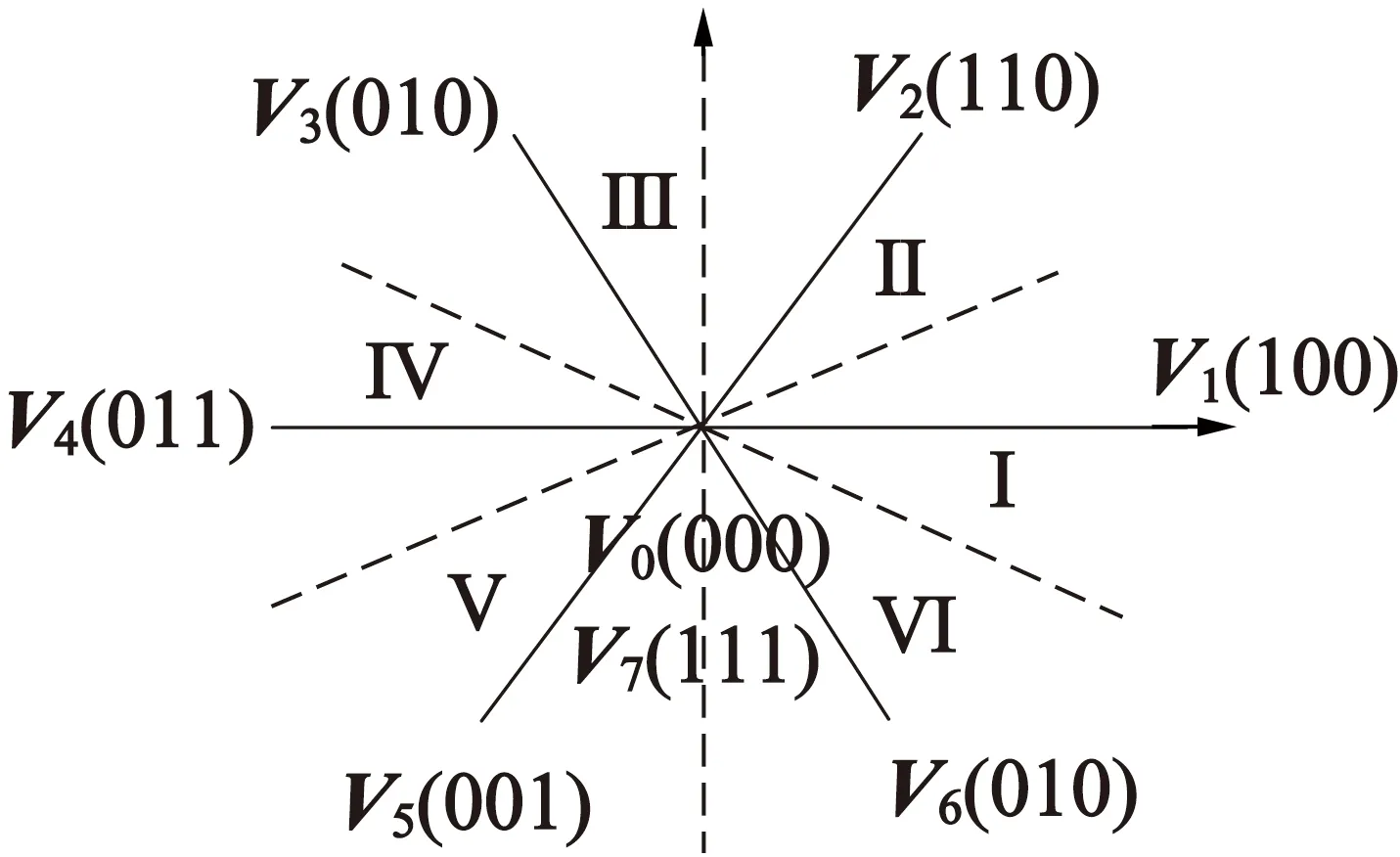
图1 电压空间矢量
通过式(5)可以计算得到两相旋转坐标系下的下一时刻电流预测值,由式(2)和式(3)可以计算得出下一时刻磁链和转矩的预测值。
1.3 有限控制集模型预测DTC控制
模型预测DTC是为了使测量的转矩和磁链与给定转矩和磁链之间的误差最小,因此设计代价函数:
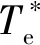
(8)
式(7)的代价函数控制目标:第一项为电磁转矩跟踪参考转矩;第二项为定子磁链跟踪参考值;第三项为限定定子电流幅值的函数,函数表达式:
(9)
式中:imax为定子电流限幅值。若指定的电压矢量作用下产生的预测电流值超过了imax,则代价函数g=∞,排除该电压矢量;如果预测电流值没有超过imax,则代价函数的值取决于前面两项。
模型预测DTC框图如图2所示。
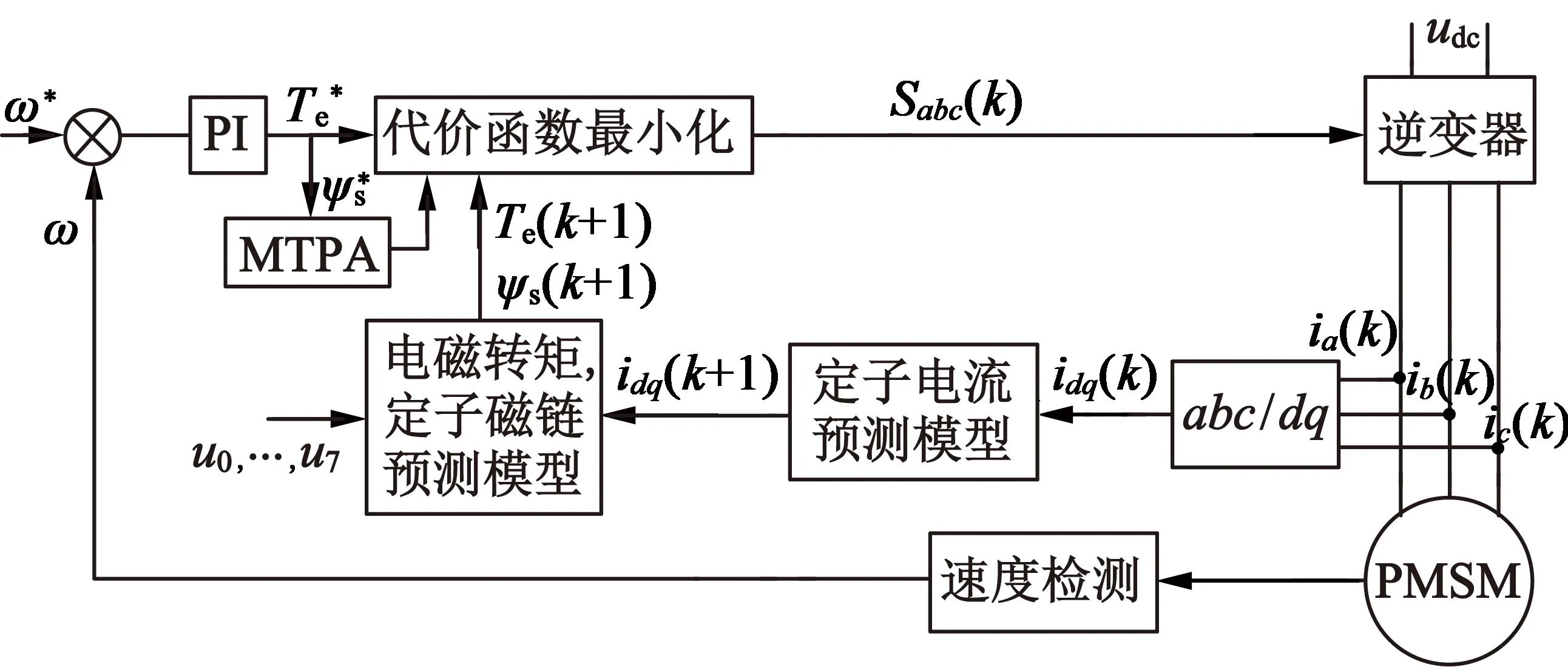
图2 模型预测DTC框图
1.4 权重系数模糊控制器的设计
由于代价函数中权重系数的确定决定了系统的动态性能,本文介绍了通过模糊逻辑控制策略在线确定其值的方法,以便合适地选择最佳切换状态Sabc(k)。
模糊逻辑控制器的输入为磁链差Δψs(k)和转矩差ΔTe(k),输出为磁链权重系数δψ和转矩权重系数δT,输入输出的模糊集为{NB(负大),NS(负小),PS(正小),PB(正大)},隶属函数采用Gaussmf设计。转矩模糊控制规则如下:
if ΔTeis PB, thenδTis PB;
if ΔTeis PS, thenδTis PS;
if ΔTeis NS, thenδTis PS;
if ΔTeis NB, thenδTis PB。
磁链的模糊控制规则与上面类似。当转矩或磁链误差大的时候,应该增加其对代价函数的影响;当转矩或磁链误差较小时,应该适当减小其对代价函数的影响。模糊模型预测DTC框图如图3所示。
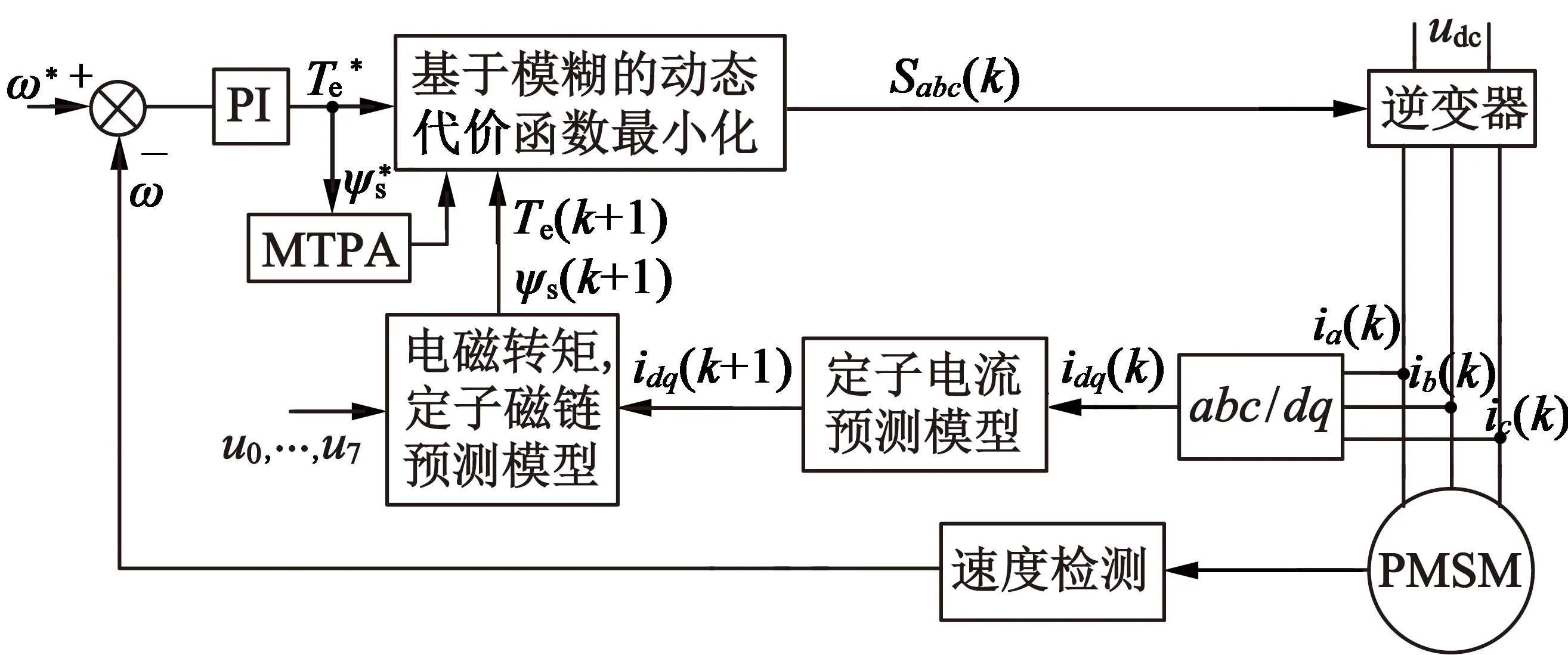
图3 模糊模型预测DTC框图
模糊模型预测DTC算法如下:
(a) 测量得到定子三相电流ia(k),ib(k),ic(k),转子位置θr(k),计算得到id(k),iq(k)和ωr(k)。
(b) 对于每一个电压矢量,通过PMSM的离散时间模型预测,得到下一时刻电流id(k+1),iq(k+1),从而计算出每一个电压矢量下的下一时刻电磁转矩值Te(k+1)和定子磁链值ψs(k+1)。
(d) 通过模糊逻辑控制动态地确定代价函数中的权重因子δT,δψ。
(e) 选择使代价函数值最小的电压矢量,产生相应的开关状态,作用于三相逆变器。
2 模糊自抗扰转速控制器的设计
2.1 ADRC原理
非线性ADRC由韩京清研究员提出[7],针对PID控制器的缺陷进行了改进,解决了PID控制器在响应快速性和超调之间的矛盾问题。大量工程研究表明,自抗扰策略对非线性控制系统有较强的鲁棒性和适应性[9]。
ADRC主要由线性TD、ESO、NLSEF组成。TD用来可靠获取微分信号,以安排过渡过程来减少因突变而引起的系统超调;ESO用来估计系统总扰动;NLSEF用来改进控制效果。以一阶自抗扰系统为例,图4为一阶ADRC框图。
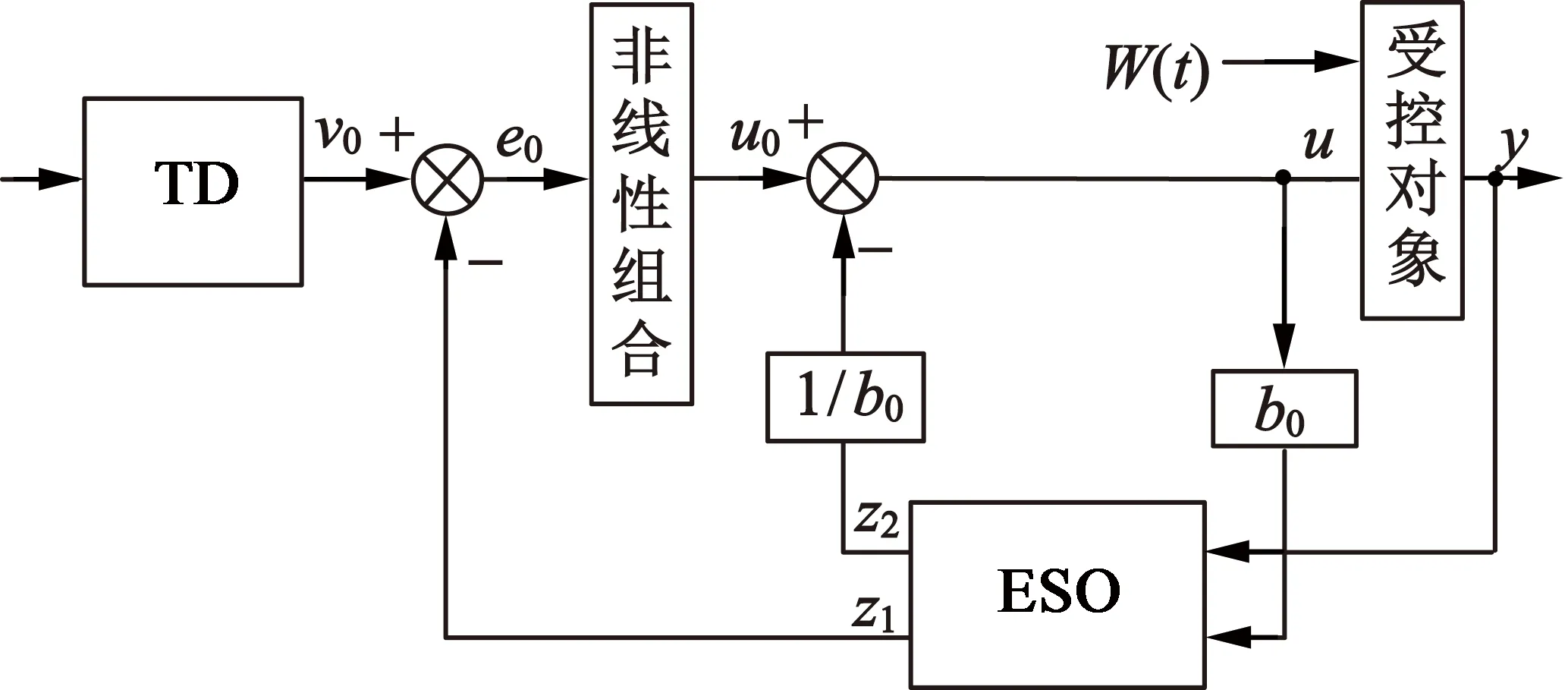
图4 一阶ADRC原理图
设一阶系统:
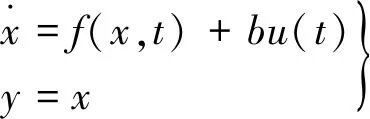
(10)
式中:f(x,t)为总扰动;x为可测状态;b为控制系数;u(t)为系统输入。
本文对一阶ADRC进行优化,将比例环节P代替TD环节,减少了典型ADRC中的非线性反馈环节,增强系统实时性。
优化后的一阶ADRC的算法[10]如下:
二阶ESO:
(11)
NLSEF:
(12)
扰动补偿:
(13)
式中:e(k)为观测误差;v0为设定值;y为被控对象的输出值;h为采样周期;z1为y的跟踪信号;β1,β2为输出误差校正增益;z2为总扰动的估计值;u为控制量;kp为反馈控制律比例系数;b0为补偿系数。
从式(11)~式(13)可以看到,优化后的一阶ADRC有4个不确定参数,分别为β1,β2,kp和b0,其中输出误差校正增益β1,β2主要由控制器的离散控制周期h决定,一般取β1=1/h,β2=1/(5h2);参数b0对估计值的精度要求也不高,误差在30%以内,不影响控制效果。
2.2 模糊ADRC原理
本文引入模糊逻辑控制器,来在线自整定参数kp,图5为优化后的一阶模糊ADRC。
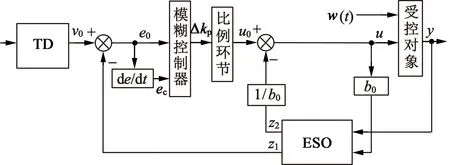
图5 一阶模糊ADRC结构图
图5中,模糊控制器的输入为v0与z1之差e0和其偏差变化率ec,输出为Δkp。在它们的论域上各定义了5个语言子集为{负大(NB),负小(NS),零(ZO),正小(PS),正大(PB)}。取e0和ec的基本论域为[-6,6],Δkp的基本论域为[-1,1],选择输入输出的隶属度函数为三角形隶属度函数,模糊推理采用Mamdani型。当e0较大时,为提高响应速度,Δkp取大值;当e0较小时,为了防止超调和系统尽快稳定,Δkp取小值;当e0和ec同号时,输出向偏离稳定值的方向变化,应适当增加Δkp,反之适当减小Δkp。根据控制规则,查得修正参数Δkp后,代入公式:
kp=kp0+Δkp(14)
计算所得为比例环节的参数。
2.3 转速控制器的设计
PMSM的运动方程:
(15)
式中:Tm为负载转矩;J为转动惯量;Te为电磁转矩;B为阻力系数;ωr为电机转速。
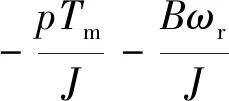
当作控制系数b,可测状态x为ωr,系统输入u(t)为Te,可得状态方程与式(10)相同,故可根据式(11)~式(13)设计一阶模糊自抗扰转速控制器,如图6所示。
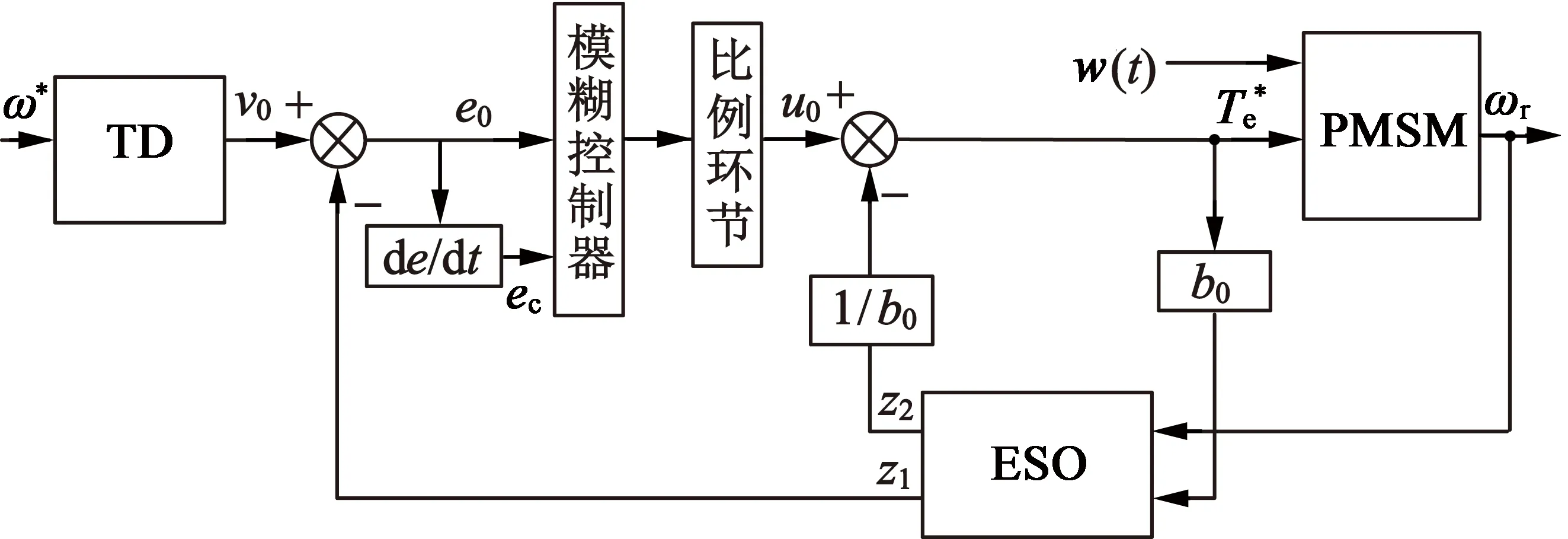
图6 一阶模糊自抗扰转速控制器
3 仿真验证
为了验证本文方案的有效性,在MATLAB/Simulink上搭建了仿真模型进行验证,模糊模型预测DTC框图和仿真模型如图7、图8所示。在仿真系统中,PMSM的参数如下:极对数p为4,定子电阻Rs为2.875 Ω,转子磁链ψf为0.175 Wb,d,q轴电感均为0.014 H,给定转速为500 r/min,转动惯量J为0.008 kg·m2,摩擦系数B为0.001,β1为10,β2为20。
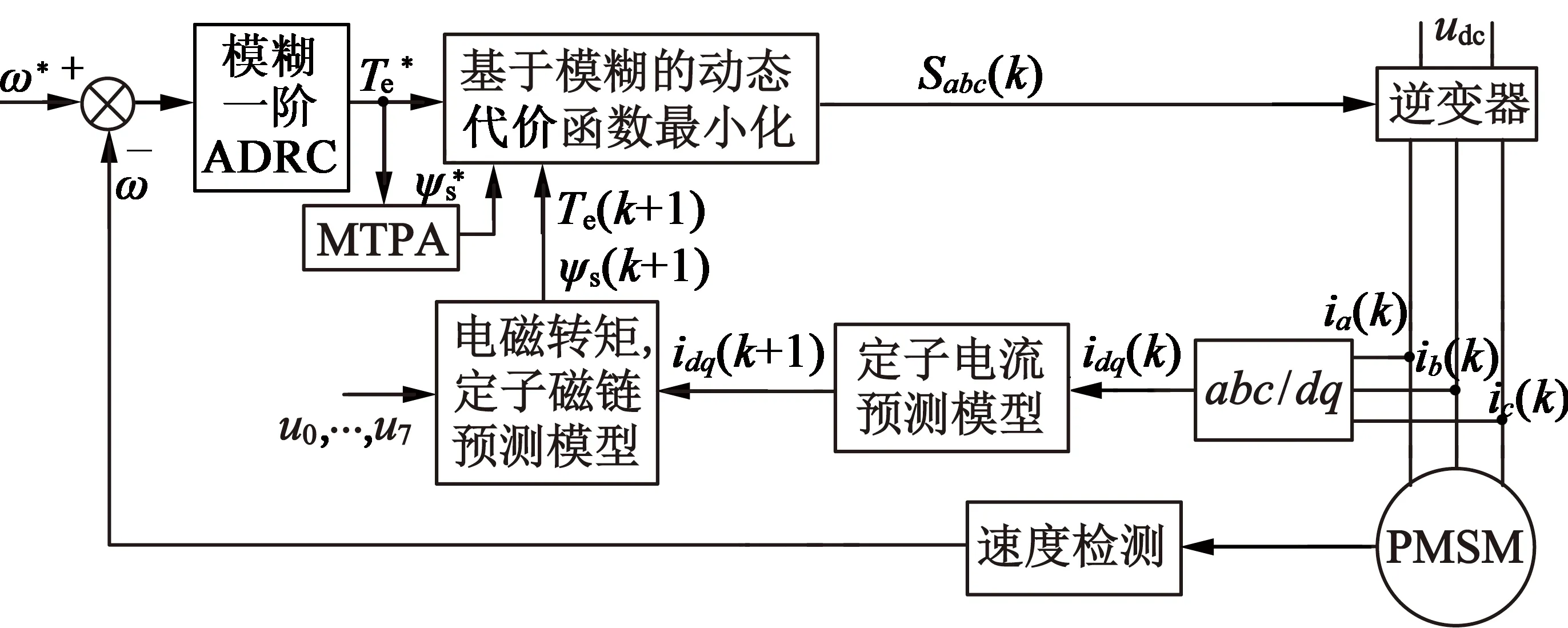
图7 基于ADRC的模糊模型预测DTC框图
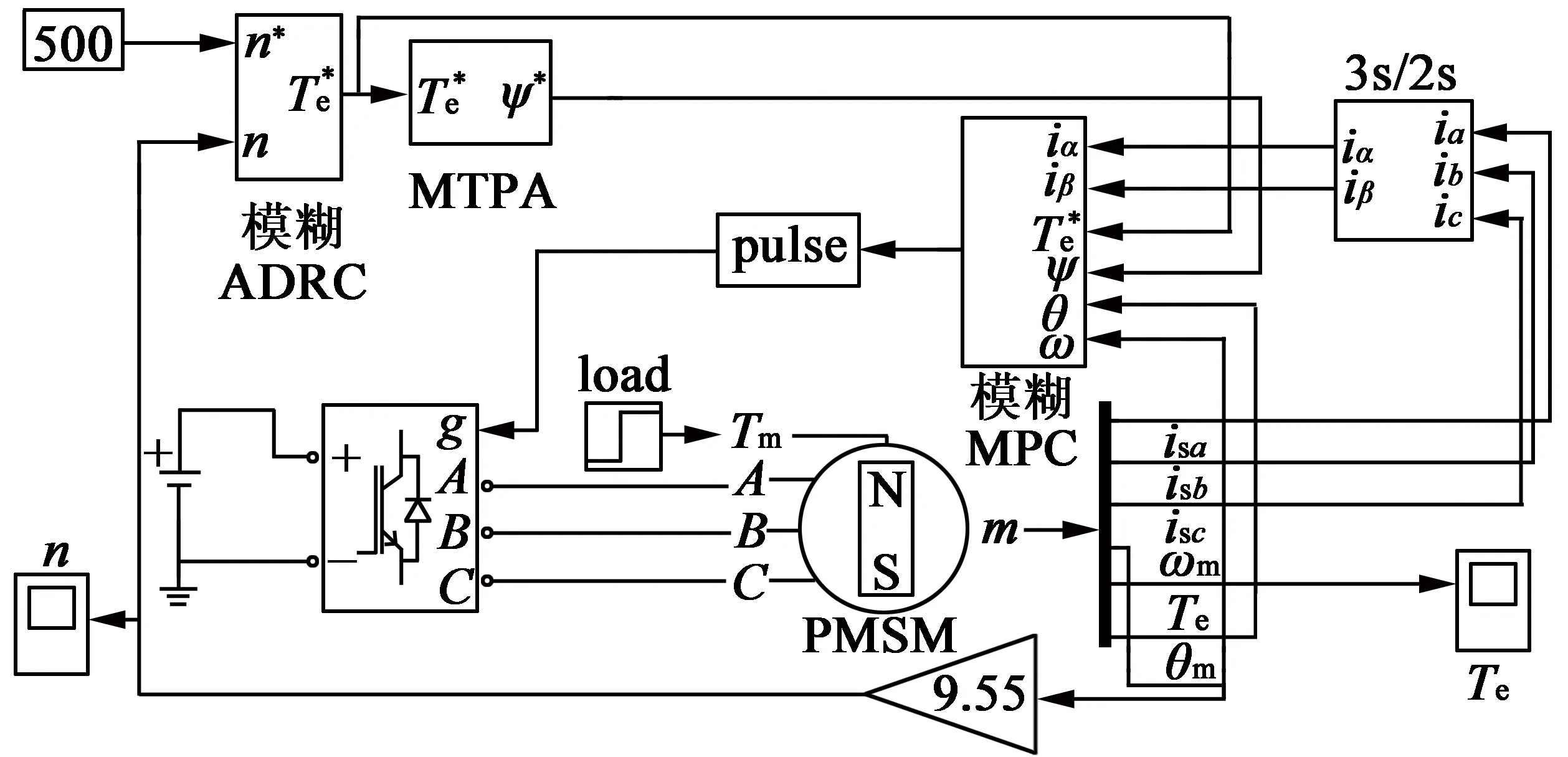
图8 模糊模型预测DTC仿真模型
当电机初始时空载运行,系统到达稳定时,在0.1 s突加3 N·m的负载转矩,外部参数变化时的转矩响应波形如图9所示。
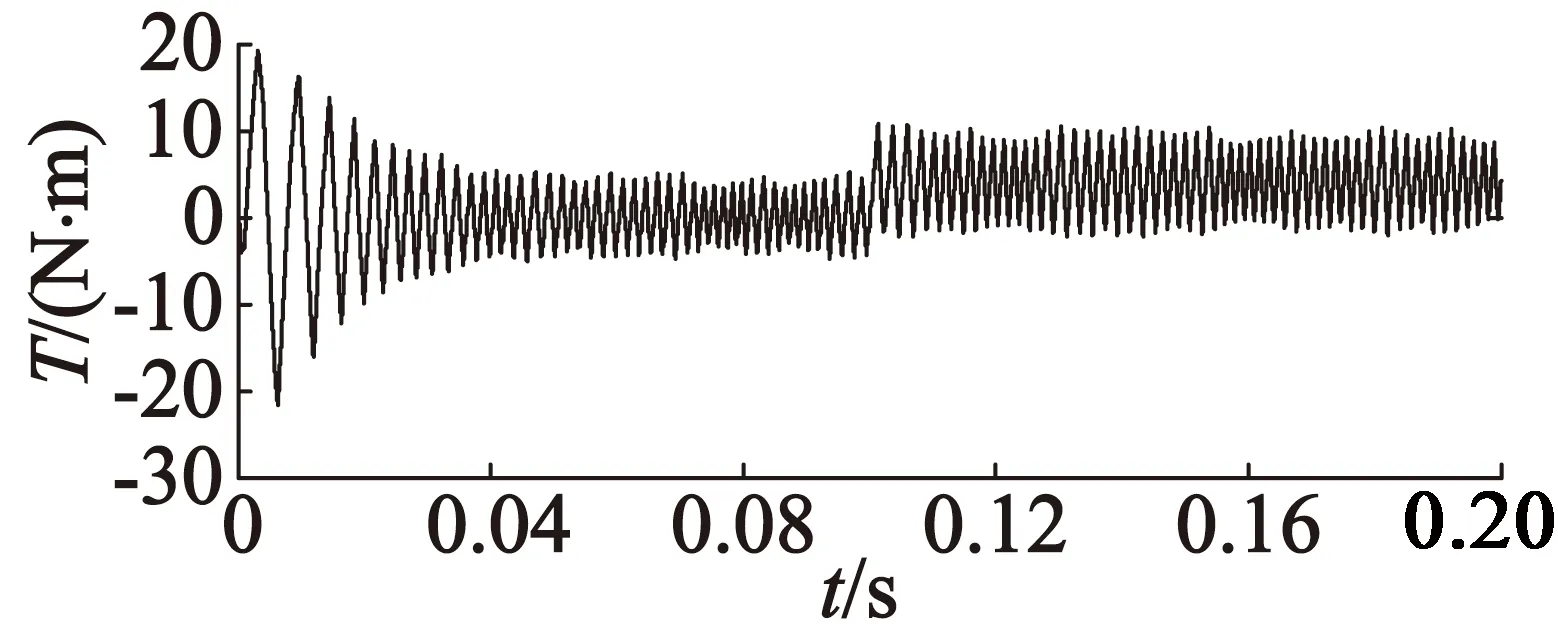
(a) 传统DTC

(b) 模型预测DTC
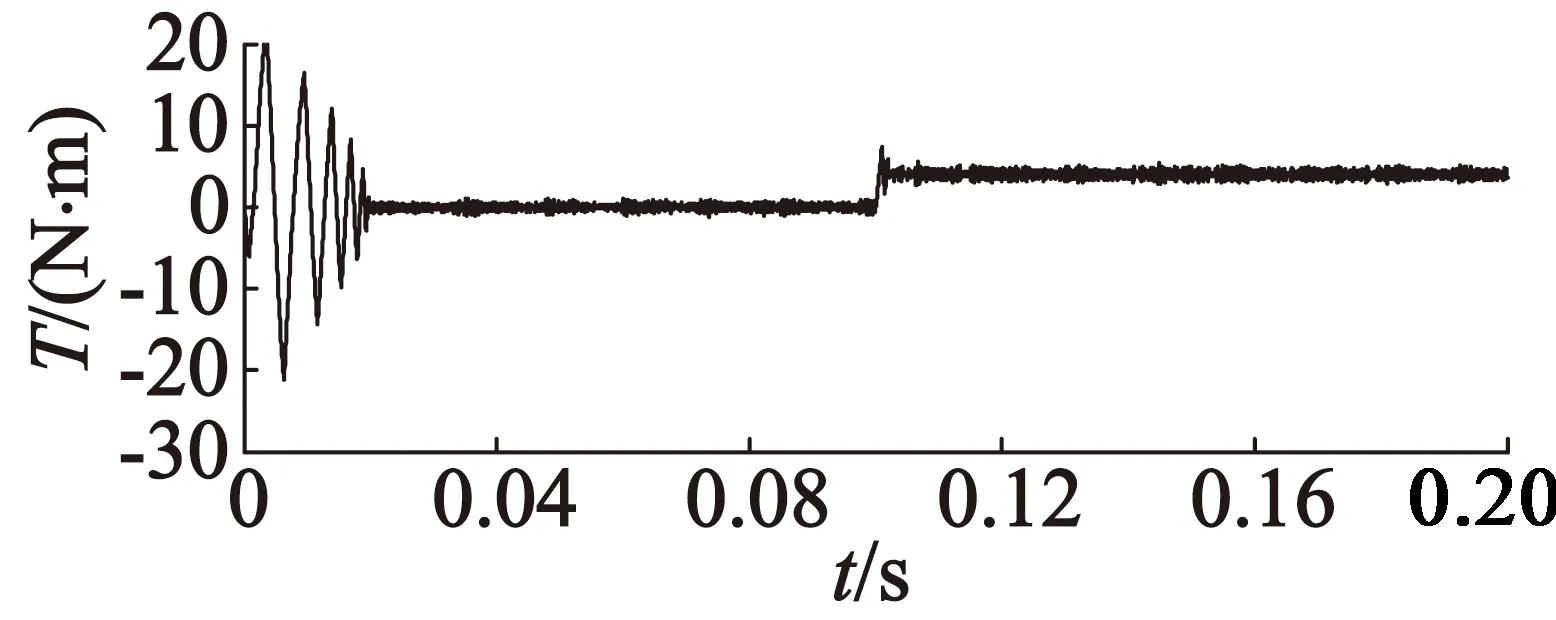
(c) 模糊模型预测DTC
从图9中可以看出,当外部参数变化时,模糊模型预测DTC相比于其他两种方法,能够大幅减小转矩脉动,对电磁转矩进行补偿。
从图10可以看出,磁链脉动明显减小,传统DTC时的磁链差在-0.02~0.02 Wb之间,而本方案下期望的磁链和实际磁链的差值在-0.001 8~0.001 8 Wb之间,磁链轨迹边缘更光滑。
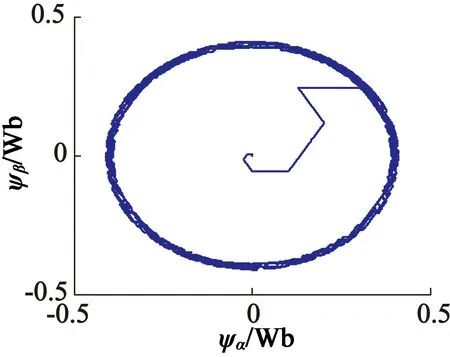
(a) 传统DTC
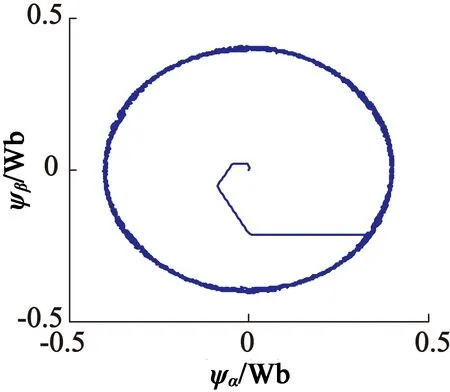
(b) 模型预测DTC
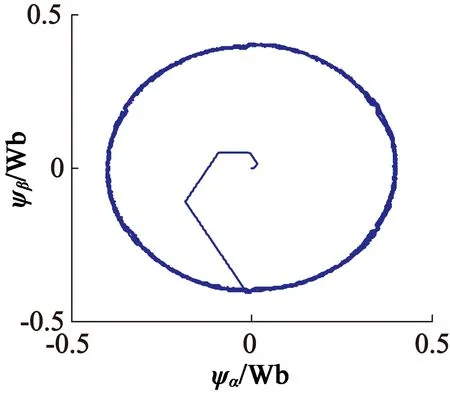
(c) 模糊模型预测DTC
图11为空载起动,在0.1 s突加3 N·m负载时的速度仿真图。从图11中可以看出,相比其他两种方式,本方案下的DTC速度跟踪快且无超调,在突加负载后,转速无明显变化,并能快速返回给定速度,能够较好地解决PID控制器带来的快速性和超调之间的矛盾。
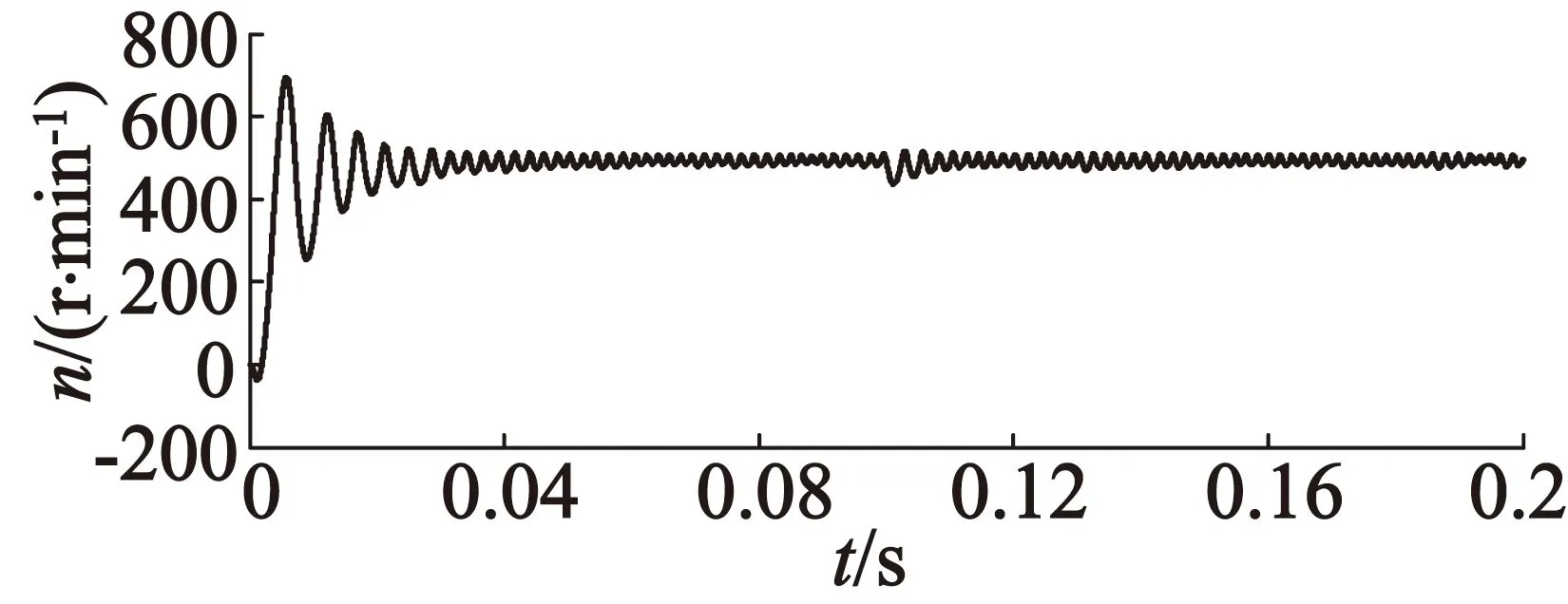
(a) 传统DTC
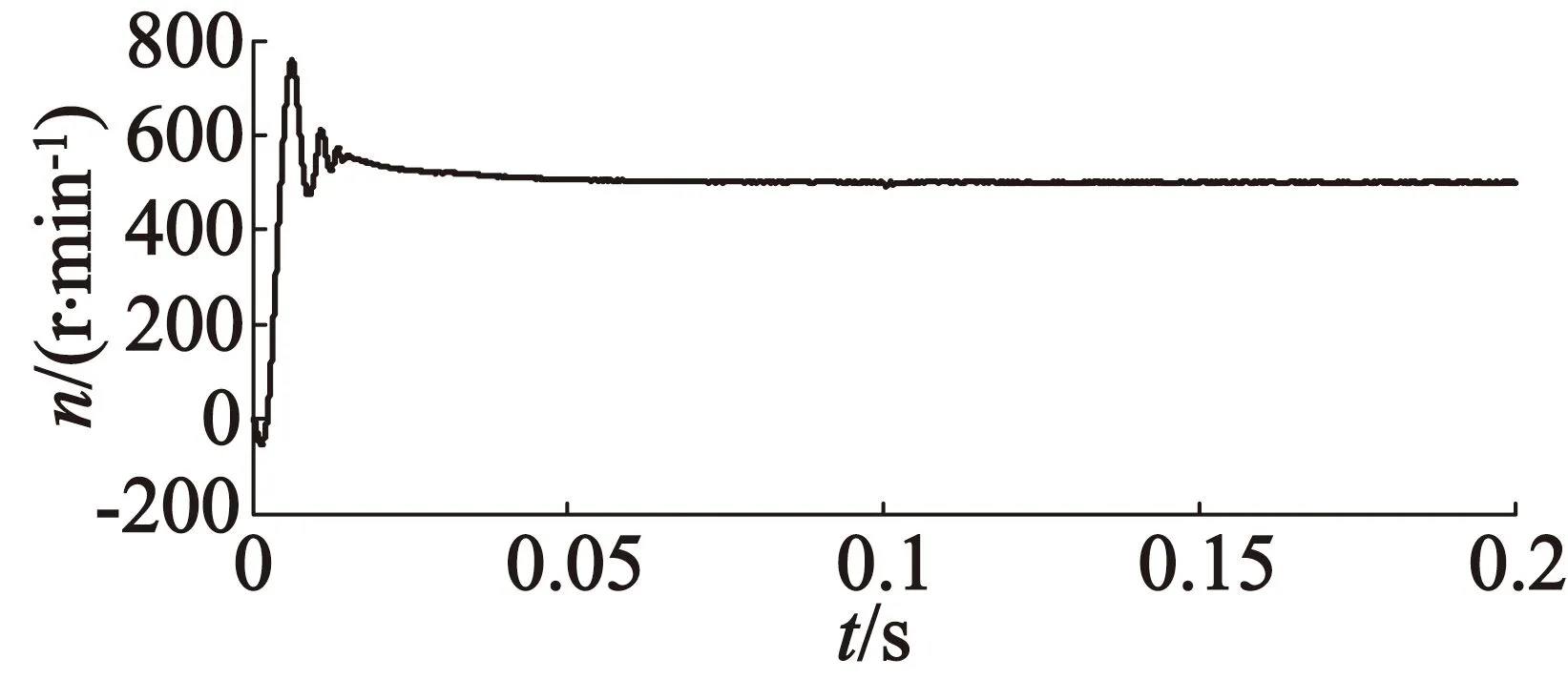
(b) 模型预测DTC
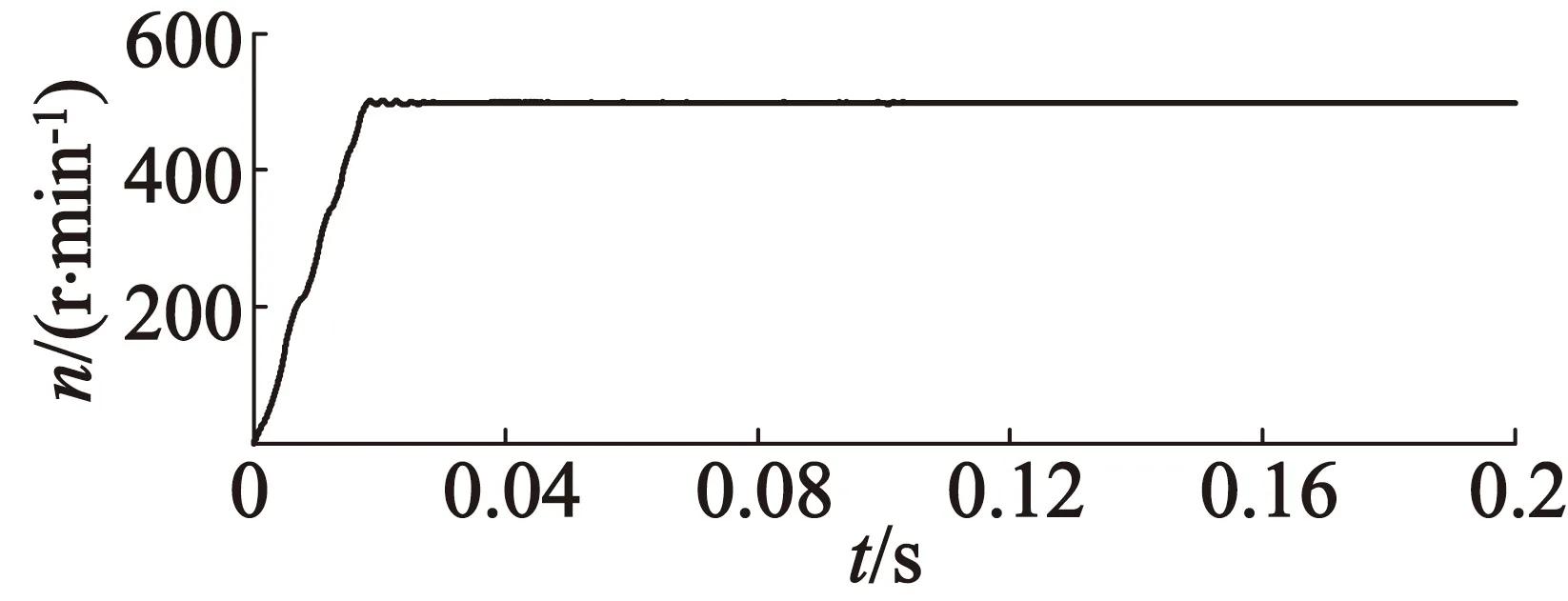
(c) 模糊模型预测DTC
4 实验验证
为了验证本方案的可行性,搭建了基于STM32的实验平台,如图12所示。实验采用额定功率1 kW,额定电压48 V,额定转速3 000 r/min的PMSM。
给定转速500 r/min,空载起动,通过串口采集转速信号,可得模型预测DTC下的转速波形n1和模糊模型预测DTC的转速波形n2,如图13所示。与传统方案相比,电机能很快响应转速命令,并且无超调,且有较好的动态性能。

图12 实验现场
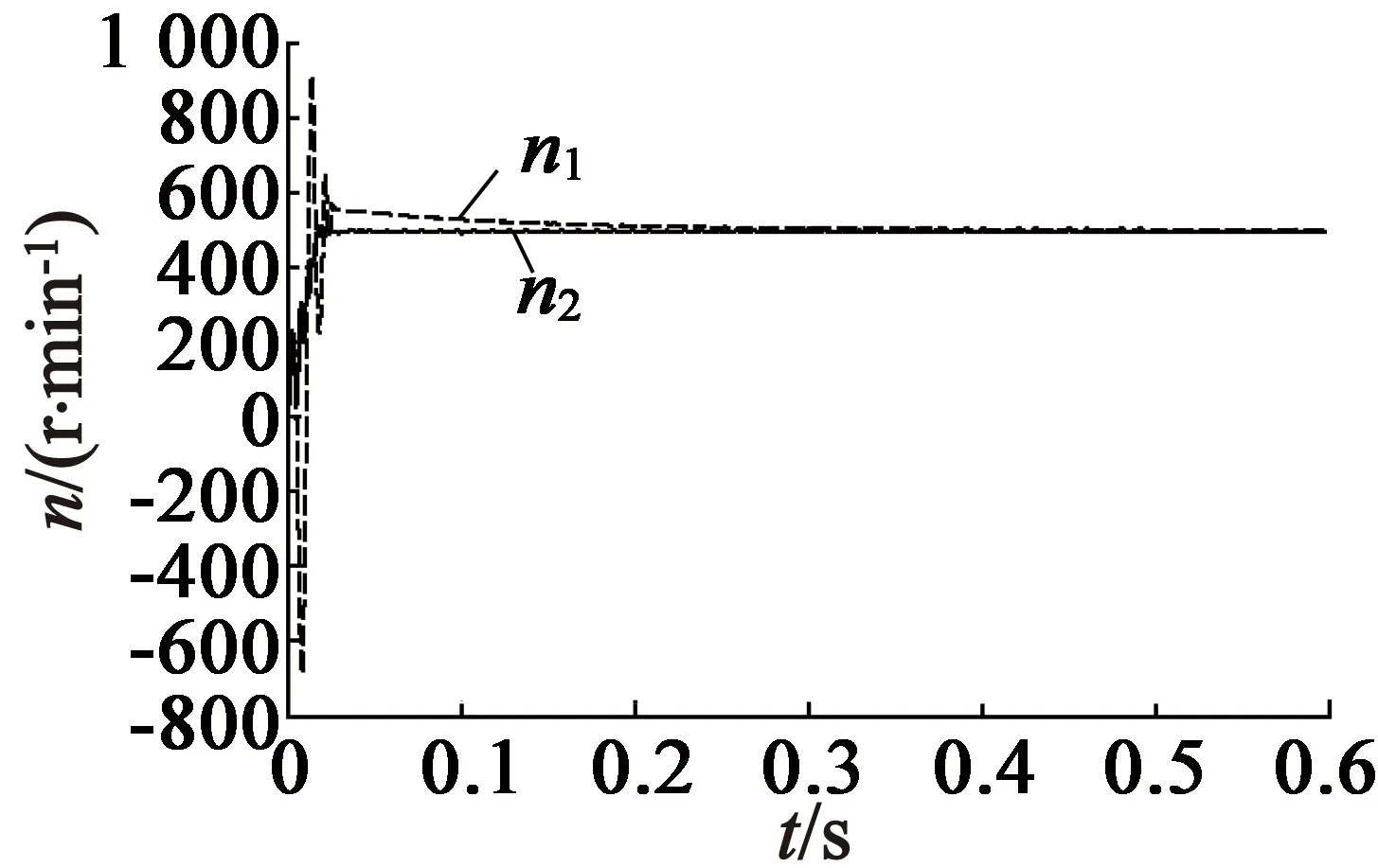
图13 实验转速波形图
5 结 语
本文建立了基于模糊模型预测DTC的PMSM模型,并进行了仿真和实验。结果表明,与传统DTC相比,模糊模型预测DTC有较好的动态和静态性能,具有磁链、转矩脉动小,抗干扰能力强,速度跟踪快,无超调等优点。

