雷诺数和界面污染程度对气泡水动力学特性的影响

庞明军，费 洋，陈小洪，郭雨晨，徐梦沁



雷诺数和界面污染程度对气泡水动力学特性的影响

庞明军1,2，费 洋1,2，陈小洪1,2，郭雨晨1，徐梦沁1

（1. 常州大学机械工程学院，常州 213164；2. 常州大学江苏省绿色过程装备重点实验室，常州 213164）

深入研究气泡界面污染程度对气泡水动力学特性的影响，对控制和改善泡状流动中气泡的运动速度和气液界面的传质和传热性能具有重要意义。为此，该文利用停滞帽模型详细研究了不同气泡雷诺数下，球形气泡界面污染程度对气泡界面参数（切向速度、压力、切应力和涡量）及其整体运动特征（尾流和阻力系数）的影响。基于停滞帽模型，通过改变帽角来定量控制气泡界面的污染程度，气泡雷诺数20≤b≤200，计算区域为轴对称结构。研究表明，在不同气泡雷诺数下，气泡界面污染程度对气泡水动力学单一物理参量的影响趋势是相似的，且界面参数在帽角处发生了突变；界面污染程度对气泡整体运动特征的影响与气泡雷诺数有关，气泡雷诺数越小，界面污染程度对阻力系数的影响越明显，而尾涡现象越弱。

气泡；水动力学；雷诺数；污染程度；泡状流动；停滞帽模型

0 引 言

因良好的传质和传热特性，泡状流广泛存在于工农业生产中，如化学反应工程、矿物浮选工程、雾化过程以及强化传热过程等。对于所有涉及泡状流动的工业过程，液相不可能一直处于绝对纯净状态。当液相含有某些微量污染物（如表面活性剂、电解质、蛋白质等）时，气液界面（气泡表面）便会受到一定的污染[1-16]。对于受污染的气泡界面，界面性质从法向无穿透边界变为无滑移边界，该变化极大地改变了气泡的界面性质、运动速度及其尾流特性，因而严重影响了气泡与周围流体间的传热和传质性能。因此，深入研究气泡界面污染程度对气泡界面和尾流特性的影响，对于改善和控制泡状流动的传质和传热性能具有重要意义。

为了理解界面受污染气泡的水动力学特性，国内外学者已开展了一些试验和数值研究。一些学者试验研究了受污染气泡的受力（阻力和升力）特征[2]，受污染气液界面对气泡上浮轨迹、尾流和传质特性的影响[3]，表面活性剂（及其结构）对气泡形状、上浮速度、阻力系数、聚合等动力学行为的影响[4-9]，以及电解质和表面活性剂的同时加入对气泡上浮速度的影响[7]。也有一些学者基于停滞帽模型、流体体积法和前沿跟踪法数值研究了简单剪切流场内表面活性剂对气泡升力系数的影响[10]、受污染气泡对槽道湍流统计量的影响[11]、球形气泡界面污染程度对气泡尾涡特征的影响[12]、幂律流体内受污染球形气泡的动量传递特征[13]、表面活性剂对气泡传质性能的影响[14]。早期相关的研究见文献[15]和[16]。

尽管一些学者针对此课题开展了一定的研究，但鉴于问题的复杂性、以及污染物种类的多样性，尚无法给出相关物理现象的定量描述以及合理的机理解释，只能针对特定的污染物（如某种表面活性剂）给出一些定性的描述和解释。因此，为了进一步理解界面受污染气泡的水动力学特征，利用停滞帽模型详细研究了雷诺数和界面污染程度对气泡界面参数（切向速度、压力、切应力和涡量）及其整体运动特征（尾流和阻力系数）的影响。

1 计算方法

鉴于停滞帽模型具有良好的理论基础，且只需求解流动方程、不需求解扩散方程，能将复杂的问题给予简单化，因此本文采用停滞帽模型进行求解。

1.1 停滞帽模型

当气泡在受污染的液体（如含微量表面活性剂溶液）内上升运动时，由于扩散和吸附的作用，起初时刻表面活性剂会均匀地聚集在整个气泡界面。随着气泡的上浮运动，气泡上部界面的表面活性剂在对流的影响下逐渐向气泡尾部（即下部）界面聚集，并降低下部界面的流动性。气泡界面表面活性剂浓度的上低下高，使浓度低的上部界面继续以吸附过程为主，而浓度较高的下部界面则以解吸过程为主。另外，气泡界面表面活性剂浓度的不均匀分布，一方面会导致表面活性剂沿着气泡界面进行扩散；另一方面还会产生一个与对流作用反向的切应力（即马兰戈尼切应力），来进一步改变气泡界面表面活性剂的分布。当气泡界面的表面活性剂在吸附、对流、解吸、扩散和马兰戈尼效应的共同作用下达到动态平衡时，气泡界面可近似看作如图1所示的停滞帽模型。该模型将气泡表面分为2部分：一部分是几乎没有表面活性剂聚集的上部界面，即可滑移界面；另一部分是聚集有表面活性剂的下部界面，即不可滑移界面。

注：θ为帽角，其大小表示气泡界面的污染程度；α为方位角，表示气泡界面上任一点与气泡前部端点的夹角。下同。

1.2 工况设置和物性参数

为了研究气泡界面污染程度对气泡水动力学特性的影响，将图2中气泡尾部无滑移界面所对应的帽角（）设为不同值，即=0、15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°和180°。上部可滑移界面和下部不可滑移界面的计算边界条件设置如图2所示。由此，=0°表示气泡界面完全干净，整个界面均有滑移速度；=180°表示气泡界面被完全污染，此时界面性质与刚性小球相似，界面无滑移速度。当气泡雷诺数b>200时，污染物在气泡界面上的分布可能不再为二维特性[13]；b<20时，气泡尾部无尾涡形成，流场较为简单[13]；因此目前所研究的气泡雷诺数范围为20≤b≤200。气泡雷诺数（b=/）的大小是通过调节液相来流速度的值来实现的，而液相的热物性参数选用常温下水的数据，即密度=998.2 kg/m3和动力黏度=1.003×10-3Pa·s。

1.3 计算区域和控制方程

鉴于20≤b≤200时，流场呈轴对称结构[13,17-18]，为了节省计算时间，采用二维轴对称模型进行计算，具体计算区域如图2所示。计算时，根据运动的相对性，假设直径为的气泡静止不动，而液相以恒速流过气泡表面。为了减少计算量、捕捉完整的尾涡结构，和避免进出口及壁面条件对计算结果的影响，参考文献[19-20]，设置液相进口距气泡中心为5、出口距气泡中心为12，壁面距气泡中心为7，为对称轴。

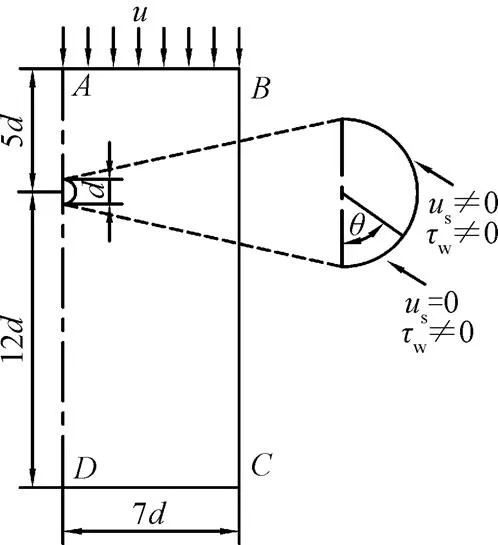
注：d为气泡直径，u为来流速度，us为界面切向速度，τw为界面切应力；θ为帽角。

考虑气液两相的不可压缩性，其连续性方程和动量方程分别为

1.4 网格划分和数值方法

整个计算区域采用四边形网格进行网格划分，为了减少计算量和捕捉气泡附近边界层的流动结构，采用非均匀网格进行网格划分，即越靠气泡表面，网格越密。另外，因气泡界面环向网格数对计算结果具有重要影响，为此对环向网格的无关性进行了检验。由于b越大，所需的环向网格越密集，因此检验时取b=200。计算表明（如图3a所示），当气泡界面环向网格数为288时，干净气泡（=0）与完全污染气泡（=180°）的阻力系数（D）不再随网格的增加而发生变化，因此将气泡界面沿环向均匀划分为288份。

培养城市会展旅游品牌就是为城市制作一张拿得出手的会展旅游名片，有助于提升成都市在游客中的影响力。想要培养成都市的会展旅游品牌，首先要找出成都市的优势产品、优势行业和优势会展。提到成都，人们往往会首先想到国宝大熊猫或者火锅、串串等具有地方特色的美食。成都市可以围绕这些知名的产品打造具有特色的会展项目，会展要具有鲜明的主题特色，定期举办，提供专业的服务，集中资源对会展旅游品牌进行大力营销推广。培养城市会展旅游品牌不仅可以促进成都市的整体会展旅游建设发展，还能提升游客的感知价值。

图3中涉及的阻力系数由式(3)求得。

式中D为阻力，N；Dτ为黏性力，N；DP为压力梯度力，N；为气泡表面切应力的流向分量，Pa；为气泡表面积，m2；为气泡表面单位法向量的流向分量。

计算时，考虑了时间变化对流动的影响。对流项采用三阶精度的QUICK格式进行离散，以减小伪扩散；单元中心的变量梯度采用最小二乘法求解，压力项采用二阶精度的离散格式；时间项采用二阶隐式离散格式，根据文献[12]，时间步长设置为0.005 s；速度和压力项采用SIMPLE算法给予耦合。为了获得完全收敛的速度和压力场，连续性方程和动量方程的残差设为10-16。

注：CD为阻力系数，Reb为气泡雷诺数，ε为计算误差。

2 结果与分析

2.1 结果准确性验证

为了检验计算结果的准确性，将不同b下干净气泡和完全污染气泡阻力系数的计算结果与文献[21]和[22]中基于试验数据的拟合式进行了对比，如图3b所示。对于干净气泡和完全污染气泡（刚性颗粒）阻力系数的拟合式如下

从图3b中可以看出，计算结果与试验拟合式基本吻合。对于完全污染气泡，D计算值与试验拟合式的误差<2%；对于干净气泡，由于忽略了气泡内部的流动，导致二者间的误差略大，但误差最大值max≈13%。可见，目前的计算结果是准确可信的。

2.2 气泡雷诺数和界面污染程度对界面参数的影响

首先分析气泡雷诺数（b）和界面污染程度（）对气泡界面物理量的影响，如图4a－图4d所示。图4a给出了b和对气泡界面切向速度（s）的影响。从图4a中可以看出，在目前研究的b范围内，b对s随的变化趋势几乎没有影响。也就是说，当界面污染程度（）相同而气泡雷诺数不同时，s随的变化趋势是相似的，仅存在数值上的差异；气泡雷诺数越大，s的值越大。此外，图4a还表明，界面污染程度（）对s有极大的影响。对于干净气泡（=0），除了前后2个驻点外，s均不为0，即整个气泡界面几乎均可滑移，且越靠近气泡赤道（≈80°），s的值越大；随着界面污染程度（）的增加，s的最大值随之减小，且s不为0的区域范围也随之减小，即气泡流动界面的范围在不断减小。当气泡界面被完全污染后（=180°），界面上的s均为0，整个界面完全不能滑移。值得注意的是，当气泡界面污染程度增加到一定程度，即>45°时，因流场中速度变化的连续性，气泡尾部的阻滞效应逐渐影响到了最大对流位置（≈80°），致使s的最大值下降明显，且其所对应的界面位置也发生了明显的前移（即减小）。上述现象表明，气泡尾部界面受污染后，局部界面流动性的减小会严重影响气泡前部界面的流动特征。

图4b给出气泡雷诺数（b）和界面污染程度（）对界面无量纲压力（*）的影响，其定义为

式中0为远离气泡界面处流场的压力，Pa。

与气泡界面切向速度（s）随的变化趋势相似，当界面污染程度（）相同时，b对*随的变化趋势影响不大，仅是数值上有些许差异；b越大，气泡前后两侧（即迎流面和背流面）的压差越小。该现象表明：b的增加会减小气泡上下两侧压差对D的贡献；也就是说，相同界面污染程度下，b越大，而D越小。然而，界面污染程度（）对*随变化趋势的影响却非常显著。当b相同时，随着的增加，*随的分布曲线由界面干净时的逐渐向界面完全污染时的演变。对于界面部分污染的气泡，其*随的分布曲线在帽角位置处（界面性质转变处）发生了向上突变。结合图4a可以看出，由于速度与压力密切相关，若帽角位置处s的减小程度越大，作为能量补偿，该位置处*向上的突变幅度也越大。此外，当b相同时，若越大，则气泡上下两侧（即迎流面和背流面）的压差越大，且b越大，该现象越明显。上述现象表明：同一b下，界面污染程度（）越大，气泡前后两侧的压差对D的贡献越大；也就是说，相同b，界面污染越严重，D应越大。

图4c给出气泡雷诺数（b）和界面污染程度（）对界面切应力（w）的影响。图中表明，同一下，b对w随变化趋势的影响几乎相同，界面上相同位置（）处w的值随b的增大而减小。这表明对于相同污染程度的气泡，b的增加导致w对D的贡献减小。结合图4b界面压力随的变化趋势可以断定，对于相同污染程度的气泡，b越大而D越小。此外，在相同b下，对w的影响较为显著。对于干净气泡（=0），其界面上的w均为0；对于完全污染气泡（=180°），除了前后驻点和流动转折点外，其界面上的w均不为0；对于部分污染气泡，干净界面上的w等于0，受污染界面上的w不等于0，且w在帽角附近因界面流动性的突变而发生了阶跃现象。该阶跃现象的强弱与有关，当污染界面延伸到气泡赤道附近（即≈ 80°）时，w的阶跃程度取得极大值；这是因为在帽角≈ 80°附近，s减小的幅度（即梯度）最大。

图4d给出气泡雷诺数（b）和界面污染程度（）对界面涡量（）的影响。从图4d可以看出，同一下，随着b的增加，帽角附近界面流动性的突变会导致s降低幅度（即梯度）的增大，进而导致的值也随之增大。的增大意味着界面流动越易分离，尾涡越易生成。此外，当b相同时，其界面越干净，界面上的值越小，则界面流动越难分离，尾涡越难生成。与w随的变化趋势相同的是，也在帽角位置处发生了突变，且最大突变值也出现在气泡赤道附近（即≈ 80°）。随着受污染界面向气泡上表面逐渐延伸，即当>80°时，虽然界面上的突变量随之减小，但整个界面上的值却随之增加，因此气泡界面污染越严重，其尾涡越易形成。

图4 气泡界面参数

为了进一步检查界面涡量值对尾涡形成的影响，表1给出了气泡雷诺数（b）和界面污染程度（）对气泡尾部流动的影响。从表1中可以看出，对于界面污染程度相同的气泡，b越大，尾涡越易形成；在相同b下，界面污染越严重，其尾涡也越易形成。由此可知，气泡尾流的上述表象与前文（即图4d）的推测一致。

表1 气泡尾流分布

注：为流速。Note:is velocity.

2.3 气泡雷诺数和界面污染程度对气泡阻力系数的影响

分析气泡阻力系数（D）的变化，可以了解气泡雷诺数（b）和界面污染程度（）对气泡整体运动特征的影响。图5给出b和对D的影响。对于相同的b，当气泡界面受轻度污染（即小于某个临界值，称为第一临界值）时，D无明显变化；随着界面污染程度（）的增大，D快速增加；当气泡界面达到重度污染（即大于某个临界值，称为第二临界值）时，D又基本保持不变。界面轻度污染对应的第一临界值和界面重度污染对应的第二临界值与b有关；b越大，第一临界值越大，而第二临界值却越小。由式（3）和式（4）可知，D的上述变化源于界面参量*和w的综合影响。此外，对于界面污染程度相同的气泡，b越大，则D越小，但D的减小幅度又与界面污染程度有关，界面污染程度越大，D的减小幅度越明显。这表明因b和的改变引发界面参量*和w的变化对D的影响不是一个简单的线性关系，而是一个复杂的非线性关系。

图5 气泡雷诺数和界面污染程度对阻力系数的影响

综合目前的分析可知，气泡界面上*和w在帽角附近的局部突变，不会对D产生直接影响，即D的变化趋势不是直接体现为帽角处*和w的阶跃程度，而是取决于气泡整个界面上压力和切应力的改变。

3 结 论

1）对于目前所调查的气泡雷诺数范围（20≤b≤200），气泡界面污染程度对界面和尾流特性的影响是相似的，界面污染程度越大，界面参数分布和气泡尾流特征与刚性小球的越相近。

2）对于界面部分污染的气泡，界面参数（如：切向速度、压力、切应力和涡量）在帽角位置附近发生了突变，突变值大小与帽角有关；在80°帽角附近区域，各参数的突变值最大，而且受尾部界面污染的影响，各界面参数极值对应的位置发生了前移，污染程度越大，前移越明显。

3）界面污染程度对界面压力、切应力和涡量分布的影响，导致气泡阻力系数和气泡尾流发生了变化；相同雷诺数下，污染程度越大，气泡阻力系数越大，气泡尾涡越易形成。

4）界面污染程度对局部位置界面参数的影响，似乎对气泡阻力系数和尾流的影响不大，而其对整个界面参数的整体影响，则严重影响了气泡的整体运动特性。

5）对于目前所调查的气泡雷诺数，尽管界面污染程度对界面参数的影响趋势是相似的，但其对气泡整体运动特性的影响与气泡雷诺数有关。

[1] Aoyama S, Hayashi K, Hosokawa S, et al. Shapes of single bubbles in infinite stagnant liquids contaminated with surfactant[J]. Experimental Thermal and Fluid Science, 2018, 96: 460－469.

[2] Rastello M, Marié J L, Lance M. Clean versus contaminated bubbles in a solid-body rotating flow[J]. Journal of Fluid Mechanics, 2017, 831: 592－617.

[3] Huang J, Saito T. Discussion about the differences in mass transfer, bubble motion and surrounding liquid motion between a contaminated system and a clean system based on consideration of three-dimensional wake structure obtained from LIF visualization[J]. Chemical Engineering Science, 2017, 170: 105－115.

[4] Arkhipov V A, Vasenin I M, Usanina A S. Dynamics of bubble rising in the presence of surfactants[J]. Fluid Dynamics, 2016, 51(2): 266－274.

[5] Tan Y H, Finch J A. Frother structure-property relationship: Effect of hydroxyl position in alcohols on bubble rise velocity[J]. Minerals Engineering, 2016, 92: 1－8.

[6] Tan Y H, Finch J A. Frother structure-property relationship: Effect of alkyl chain length in alcohols and polyglycol ethers on bubble rise velocity[J]. Minerals Engineering, 2016, 95: 14－20.

[7] 邓丽君，李国胜，曹亦俊，等. 浮选起泡剂对气泡兼并行为的影响研究[J]. 中国矿业大学学报，2017，47(2)：410－414.

Deng Lijun, Li Guosheng, Cao Yijun, et al. Effect of flotation frothers on bubbles coalescence behavior[J]. Journal of China University of Mining & Technology, 2017, 47(2): 410－414. (in Chinese with English abstract)

[8] 裴明敬，朱婷婷，杨晶晶，等. 环境友好型生物表面活性剂对浮选气泡动力学的影响研究[J]. 高校化学工程学报，2013，27(6)：985－990.

Pei Mingjing, Zhu Tingting, Yang Jingjing, et al. Study on effects of environment-friendly biosurfactants on bubble hydrodynamics in flotation column[J]. Journal of Chemical Engineering of Chinese Universities, 2013, 27(6): 985－990. (in Chinese with English abstract)

[9] Jarek E, Warszynski P, Krzan M. Influence of different electrolytes on bubble motion in ionic surfactants solutions[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2016, 505: 171－178.

[10] Hayashi K, Tomiyama A. Effects of surfactant on lift coefficients of bubbles in linear shear flows[J]. International Journal of Multiphase Flow, 2018, 99: 86－93.

[11] Lu J C, Muradoglu M, Tryggvason G. Effect of insoluble surfactant on turbulent bubbly flows in vertical channels[J]. International Journal of Multiphase Flow, 2017, 95: 135－143.

[12] 费洋，庞明军．球形气泡界面变化对尾涡性质和尺寸的影响[J]. 化工学报，2017，68(9)：3409－3419.

Fei Yang, Pang Mingjun. Influence of interface change for spherical bubble on vortex characteristic and size[J]. CIESC Journal, 2017, 68(9): 3409－3419. (in Chinese with English abstract)

[13] Nalajala V S, Kishore N. Motion of partially contaminated bubbles in power-law liquids: Effect of wall retardation[J]. International Journal of Mineral Processing, 2015, 140: 8－18.

[14] Fleckenstein S, Bothe D. Simplified modeling of the influence of surfactants on the rise of bubbles in VOF-simulations[J]. Chemical Engineering Science, 2013, 102: 514－523.

[15] Takagi S, Matsumoto Y. Surfactant effects on bubble motion and bubbly flows[J]. Annual Review of Fluid Mechanics, 2011, 43: 615－636.

[16] Cuenot B, Magnaudet J, Spennato B. The effects of slightly soluble surfactants on the flow around a spherical bubble[J]. Journal of Fluid Mechanics, 1997, 39: 25－53.

[17] Fei Y, Pang M J. The influence of interface contaminated degree on the wake characteristics of a spherical bubble at moderate Reynolds number under the condition of isothermal flow[J]. International Journal of Heat and Mass Transfer, 2018, 121: 79－83.

[18] Reddy C R, Kishore N. Wall retardation effects on flow and drag phenomena of confined spherical particles in shear-thickening fluids[J]. Industrial & Engineering Chemistry Research, 2012, 51: 16755－16762.

[19] 任安禄，李广望，邹建峰. 中等雷诺数圆球绕流的数值研究[J]. 浙江大学学报：工学版，2004，38(5)：644－648.

Ren Anlu, Li Guangwang, Zou Jianfeng. Numerical study of uniform flow over sphere at intermediate Reynolds numbers[J]. Journal of Zhejiang University: Engineering Science, 2004, 38(5): 644－648. (in Chinese with English abstract)

[20] Tomboulides A G, Orszag S A. Numerical investigation of transitional and weak turbulent flow past a sphere[J]. Journal of Fluid Mechanics, 2000, 416: 45－73.

[21] Mei R, Klausner J F, Lawrence C J. A note on the history force on a spherical bubble at finite Reynolds number[J]. Physics of Fluids, 1994, 6(1): 418－420.

[22] Mei R. History force on a sphere due to a step change in the free-stream velocity[J]. International of Journal Multiphase Flow, 1993, 19: 509－525.

Influence of Reynolds number and interfacial contamination degree on hydrodynamic characteristic of bubble

Pang Mingjun1,2, Fei Yang1,2, Chen Xiaohong1,2, Guo Yuchen1, Xu Mengqin1

(1.,,213164,; 2.,,213164,)

The bubble flow is extensively encountered in natural and industrial fields. For the majority of bubbly flows, the liquid phase is more or less polluted, which causes the change of the interfacial state of the bubble. The state of the bubble interface has the significant effect on hydrodynamic properties around the bubble. Furthermore, the changed flow field around the bubble directly influences the heat and mass transfer properties between the bubble and the liquid phases too. Therefore, it is necessary to deeply investigate the influence of interface contaminated degree on the dynamic properties of the bubble. In this paper, a bubble with the diameter ofis considered to be suspended in a rectangular region and the fluid flows around it with the velocity of. As for the size of the region, the distances between the bubble center and the inlet, the outlet and the region wall are 5, 12 and 7, respectively. In view of the physical environment of the bubble, the bubble Reynolds number is not lager than 200, and thus the flow structure exhibits the two-dimensional properties. So the axisymmetric field can be used as the computational region, and thus the computational cost can drop greatly. Considering the contaminated degree of the bubble surface, the stagnant cap model is used. With this model, the interface contaminated degree is controlled artificially by changing boundary conditions (such as the interfacial velocity and the tangential stress) directly on the bubble surface. The cap angle, measuring from the rear stagnant point to the front edge of the contaminated interface, is used to describe the interface contaminated degree. In order to understand physical phenomena deeply, the computational cases as many as possible are designed. The cape angles representing the interfacial pollution degree are respectively designated as 0, 15°, 30°, 45°, 60°, 75°, 90°, 105°, 120°, 135°, 150°, 165° and 180°, and the bubble Reynolds numbers are selected as 20, 40, 75, 100, 150 and 200. For the present investigation, the quadrilateral grids are used to discretize the computational field. And the non-uniform grids are used in the radial direction so as to well capture flow properties near the bubble. Thus, the closer to the bubble surface the grids are, the smaller the radial grids size is. Based on the present conditions, it is fully investigated and analyzed on the influence of interfacial contamination degree on interfacial physical parameters (such as the tangential velocity, pressure, tangential stress and vorticity) and overall motion characteristics (such as the wake and drag coefficient) under different bubble Reynolds numbers. The present investigations show that, for any bubble Reynolds number, the influence of interfacial pollution levels on the physical parameters are similar, and the interfacial physical parameters have an abrupt change near the cap angle. The influences of interface contamination levels on the overall motion characteristics of the bubble are related to the bubble Reynolds number. It seems that the smaller the bubble Reynolds number is, the drag coefficient is more sensitive to the interfacial pollution level.

bubbles; hydrodynamic; Reynolds number; contamination degree; bubbly flows; stagnation cap model

庞明军，费 洋，陈小洪，郭雨晨，徐梦沁. 雷诺数和界面污染程度对气泡水动力学特性的影响[J]. 农业工程学报，2019，35(4)：99－105. doi：10.11975/j.issn.1002-6819.2019.04.012 http://www.tcsae.org

Pang Mingjun, Fei Yang, Chen Xiaohong, Guo Yuchen, Xu Mengqin. Influence of Reynolds number and interfacial contamination degree on hydrodynamic characteristic of bubble[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(4): 99－105. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.04.012 http://www.tcsae.org

2018-08-21

2019-02-15

国家自然科学基金项目（No.51376026）；江苏省“青蓝工程”资助；江苏省大学生创新创业训练计划项目（20181029032Y）

庞明军，博士，副教授，主要从事多相流动的研究。Email：pangmj@cczu.edu.cn

10.11975/j.issn.1002-6819.2019.04.012

O368

A

1002-6819(2019)-04-0099-07