基于无迹卡尔曼滤波的捷联导引头视线角速率估计方法

杨 阳，蔡正谊，陈升泽，赵 帅

(中国运载火箭技术研究院研究发展中心， 北京 100076)

随着导引头技术的发展，新型捷联式导引头及寻的技术应运而生，它取消了万向支架等机械结构，将导引头直接与飞行器刚性捷联。这项技术已成为各国重点发展的关键技术[1-2]。捷联导引头应用于实际武器系统仍有需要解决的问题[3]。由于导引头测量信号中耦合了弹体姿态信息，需要采用解耦算法；另外，导引头测量信息中缺少视线角速率信息，并且所测量的视线角信息中含有更强的噪声，无法直接提取，必须对视线角速率进行准确估计。

针对捷联导引头视线角速率的估计研究，国内外学者已开展相关方面的研究。颜东[4]为了实现捷联导引头的导引律设计，引入了“瞬态导引法”，采用卡尔曼滤波方法对捷联导引头测量信息进行处理，并利用庞德里亚金最小值原理推导出捷联最优制导律。但该算法需要已知飞行器的加速度等信息，且进行了一些假设，工程实际应用比较困难。楚德强[5]根据捷联导引头能测量视线角信息的特点，对经典导引律进行改造变形，设计了多种形式仅需要视线角信息的捷联制导律，分析了各因素对制导精度的影响以及捷联制导律的鲁棒性，验证了捷联导引律的性能和适应性。R.D.Ehrich、Smita Sadhu、Emmert RI等[6-8]对有关捷联导引头视线角速率估计方法进行了研究。姚郁等也对视线角速率提取的解耦问题进行了推导；孙婷婷等[9-10]设计了一些滤波算法，有效推动了视线角速率提取的研究。

本文以末制导武器为研究对象，根据弹体视线、弹体姿态与视线角速率的运动关系，提出了基于无迹卡尔曼滤波的捷联导引头视线角速率估计方法，克服了扩展卡尔曼滤波算法精度偏低、计算量较大的缺点，具有很好的工程应用价值。

1 解耦算法

捷联导引头测量的体视线角中包括了目标相对于惯性空间的视线角和弹体姿态角，而导弹制导所需惯性视线角速率需要从体视线角信号中去除弹体运动信息。可以通过不同坐标系的相对旋转关系推导视线角速率解耦算法[11]。

从图1可以看出，发射系转换到视线坐标系的转换有两种方法。

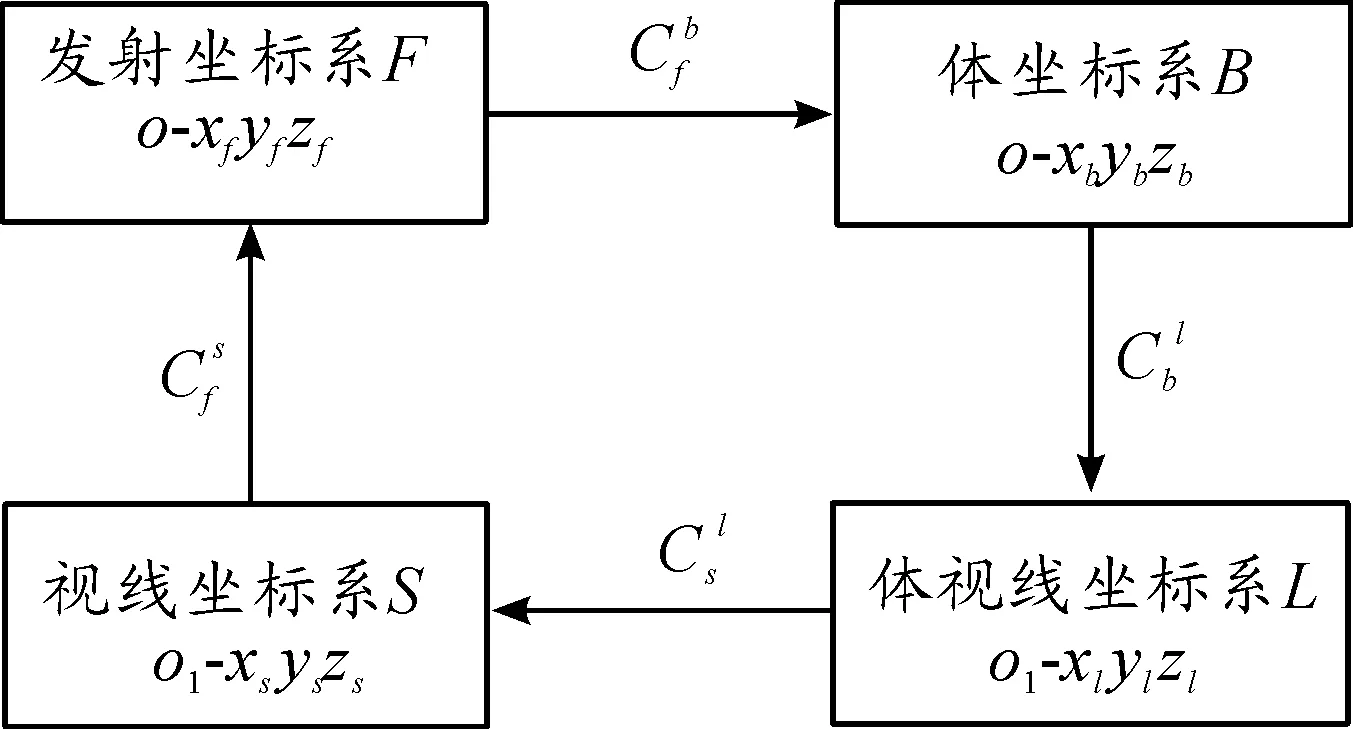
图1 坐标转换关系

方法1：由发射坐标系经弹体坐标系、体视线坐标系到视线坐标坐标系。

视线坐标系相对于发射坐标系的旋转角速度为ω′，在发射坐标系中表示为：

(1)

方法2：由视线坐标系直接到发射坐标系，可以求得ω′为：

(2)

(3)

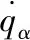
考虑到目标在体视线坐标系及视线坐标系下的位置，得到目标在体坐标系以及发射坐标系中的坐标分别为：

(4)

(5)

(6)

式中qα是在体视线下的高低角，qβ是在体视线角下的方位角。同理，可得：

(7)

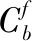
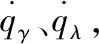
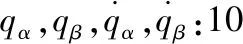
2 视线角速率估计

式(3)和式(7)可以发现获取视线角速率需要导引头测量到的信息，即两个视线角及其微分。若是量测系统并不包含噪声，使用上述算法可以有效求解出系统所需的视线角速度，但捷联导引头只能测得相对于弹体的视线角信息，其中耦合有弹体姿态运动，具有强非线性，含有大量的噪声干扰信息。因此，有必要对视线角及角速率的提取建立合适的滤波器，选取合适的滤波算法，以获取更加精确的结果。实际的导航系统中，状态方程和量测方程都是非线性的，采用传统的扩展卡尔曼滤波(Extended Kalman Filter,EKF)需要进行泰勒级数展开的线性化处理，并将一阶近似项作为原状态方程和量测方程的近似表达式。这就在高斯随机变量的实际后验均值和方差中引入误差，导致仿真结果次优，甚至引起发散。为了改善对非线性问题进行滤波的效果，Julier等人提出了无迹卡尔曼滤波方法(Unscented Kalman Filter,UKF)对非线性问题进行滤波估计。由于UKF可以有效克服EKF滤波精度偏低及需要计算雅克比矩阵的局限性，故其在组合导航系统、惯性导航初始对准、机动目标跟踪等各个领域已获得广泛的应用[12-13]。该方法在处理状态方程时首先进行了UT(Unscented Transformation)变换，使用UT变换后的状态变量进行滤波估计，以减少估计误差。

2.1 状态方程

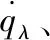
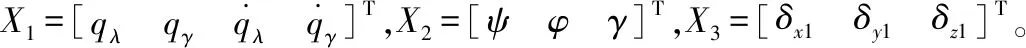
(8)

其中f1(·)由弹-目运动视线运动模型式(3)和式(7)得到，f2(·)由姿态运动模型式(9)得到。

(9)

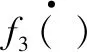
(10)

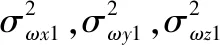
式(8)离散化后可表示为

Xk+1=F(Xk,ωk)+Wk

(11)

2.2 量测方程

由于导引头可直接测量体视线高低角和范围角qα,qβ，陀螺可实施测量弹体运动的角速率ωx1,ωy1,ωz1，将其作为量测信息。

则量测方程为

Z(t)=h[X(t),ω(t),t]+n(t)

(12)

离散化后可表示为

Zk=Hk(Xk,ωk)+Vk

(13)

2.3 UKF滤波

1) 设状态变量为n×1维，那么2n+1个σ点及其权重分别如下：

(14)

式中τ=α2(n+κ)-n是一个比例因子，κ是一个标量，取κ=2，α选取0<α<1，对于高斯分布，取β=2。

2) 每个δ采样点通过非线性函数传播，得到

y=g(Xik),i=0,…,2n

(15)

3) 其估值及方差

(16)

通过式(12)-式(14)UT变换方法，可以更为准确地求得随机分布经过非线性变换后的均值和方差，这样结合卡尔曼滤波器的一般实现框架，将UT变换分别应用于均值和方差的求解，并不断递推，便可得到UKF非线性滤波器。

UKF滤波过程如图2所示，经过式UKF滤波可得视线角和视线角速度的估计值。再基于视线角速度的估计值进行制导控制律设计，从而实现捷联导引控制。

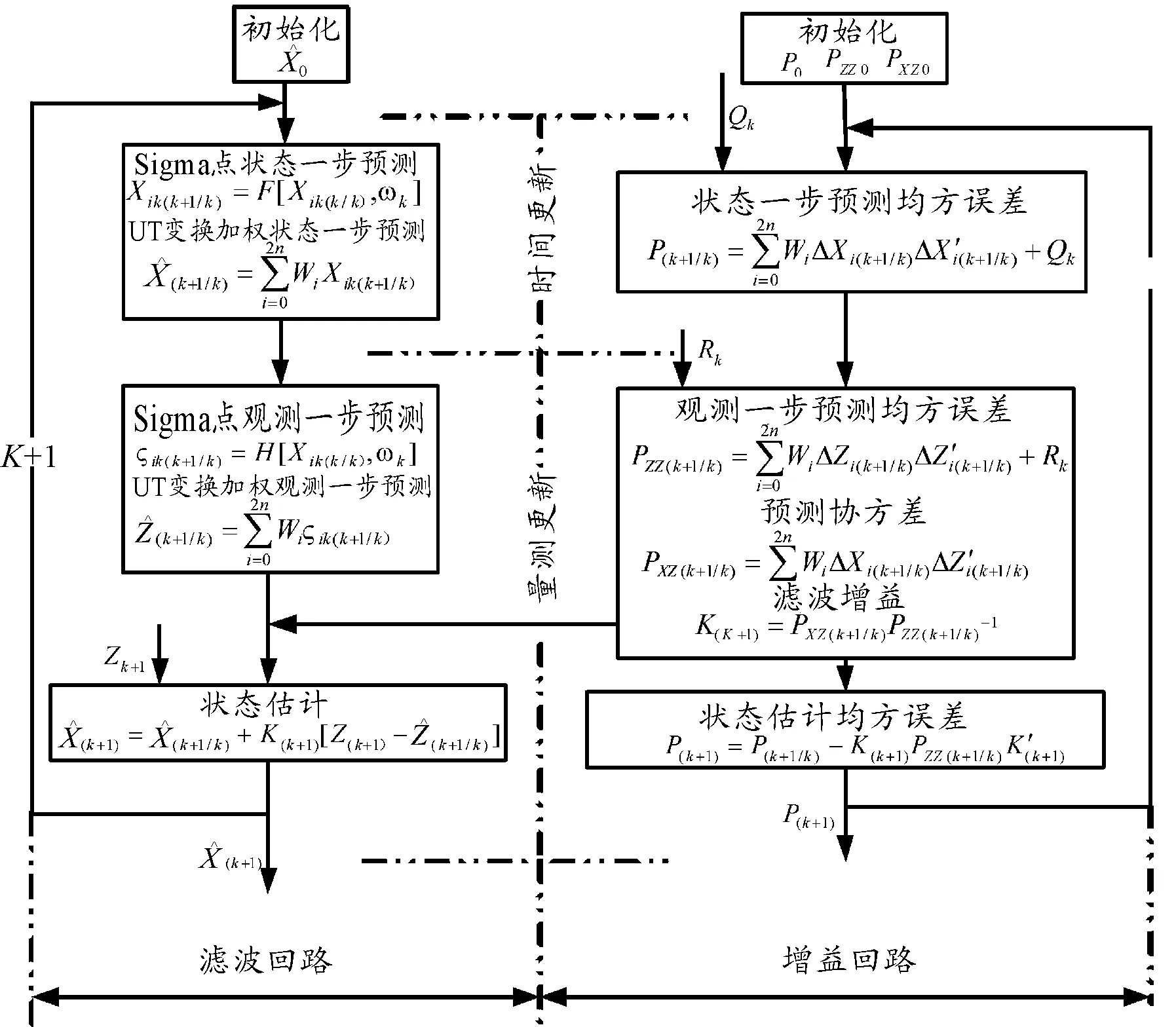
图2 UKF滤波流程

3 仿真与分析

以打击移动目标的末制导武器系统作为研究对象，采用UKF滤波对视线角速率估计，并采用经典比例导引，得到制导指令角速度为：

(17)

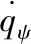
(18)

仿真时采用的初始参数如表1。

表1 初始参数(地心惯性坐标系)

末制导武器与目标初始距离为22 km，仿真时间为20 s，方位角仿真进行到19.998 s时刻，末制导武器与目标间的距离为0.475 0 m，可实现对目标的成果打击。仿真结果如图3所示。

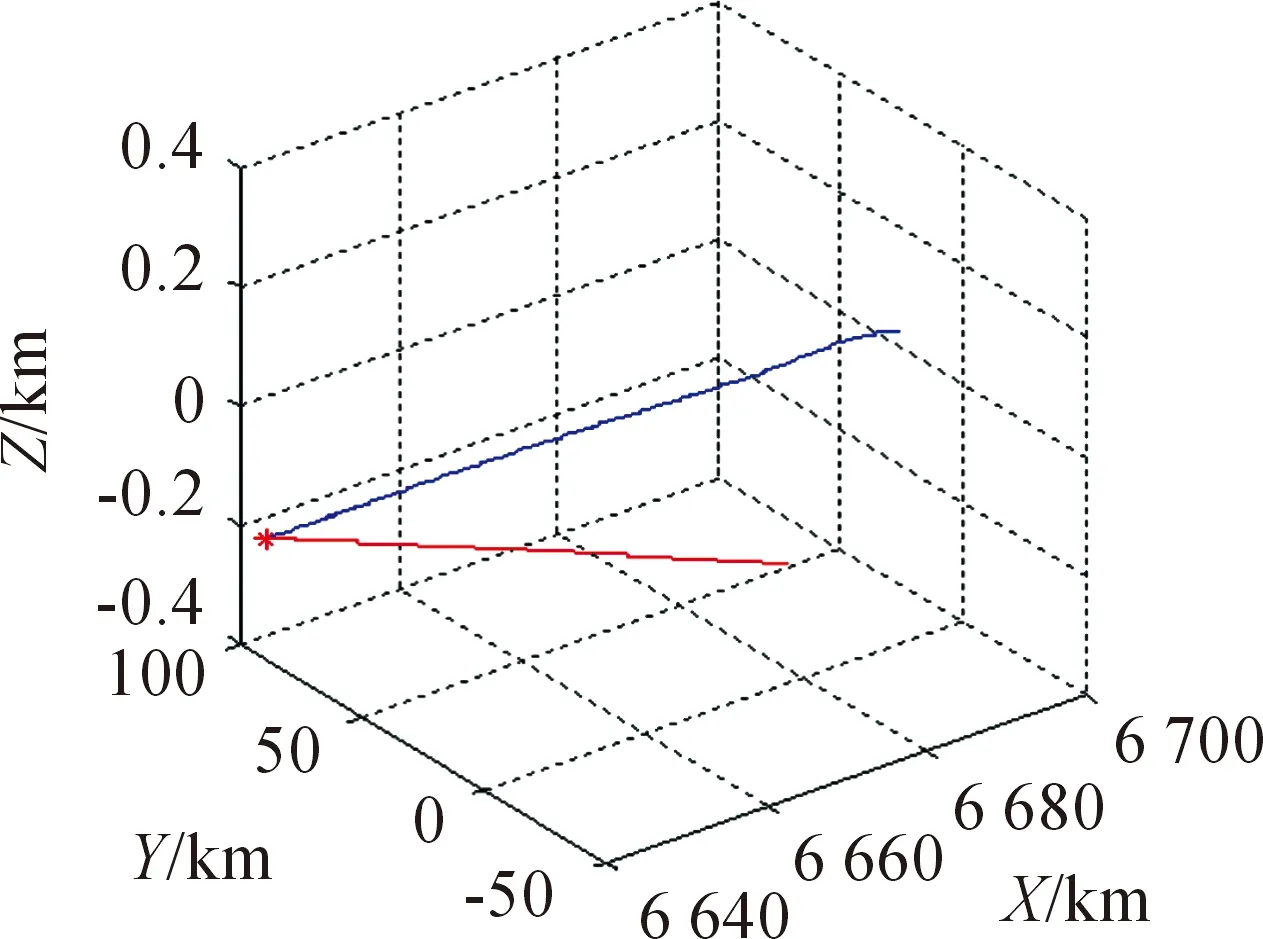
图3 末制导武器与目标运动轨迹

滤波估计视线角速率时，捷联导引头测量视线角估计误差如图4所示，视线角速率估计误差如图5所示。

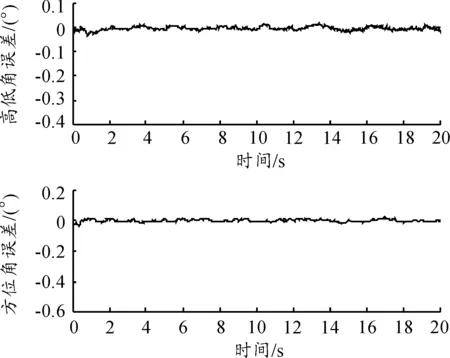
图4 捷联导引头视线角估计绝对误差

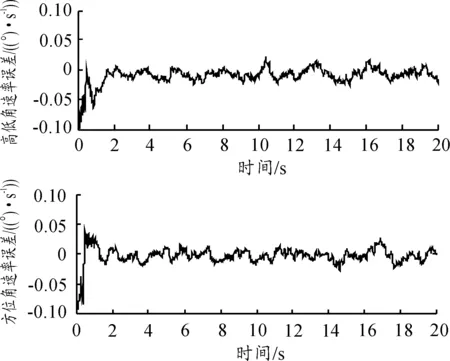
图5 捷联导引头视线角速率估计绝对误差

由仿真可以看出视线角估计精度绝对误差不大于0.05°，视线角速率估计精度绝对误差不大于0.05 (°)/s，估计精度高、收敛速度快。

4 结论

1) 本文推导了模型视线角速率解耦算法，提出了基于无迹卡尔曼滤波的捷联导引头视线角速率估计方法，克服了扩展卡尔曼滤波算法精度偏低及需要计算雅克比矩阵的局限性问题。

2) 仿真结果表明该方法具有较高的精度和动态性能，满足打击机动目标的需求，具有工程应用价值。