二元机翼的非线性气动弹性主动控制

张忠源,段静波,史凤鸣， 路 平

(1.陆军工程大学石家庄校区 无人机工程系, 石家庄 050003； 2.石家庄铁道大学 工程力学系， 石家庄 050003)

气动弹性主动控制是近几十年发展起来的试图解决飞行器结构不稳定和疲劳问题的关键技术[1]。机翼的气动弹性特性尤其是机翼的颤振为最严重的动不稳定现象，会使机翼从气流中吸收能量导致结构振动，甚至导致结构严重破坏。学者一直在探索延缓和控制颤振的各种途径，现有途径大致分为两类：被动控制和主动控制，被动控制是已广泛应用的技术，主动控制是为了弥补被动控制的不足，是一种新技术。目前，研究最多的是气动弹性主动控制。

20世纪90年代邹丛青等[2]开始了飞行器颤振主动控制问题方面控制律的研究，把最优控制理论和颤振分析的状态空间法相结合，解决了阵风缓解和稳定裕度等问题。宗捷等[3]针对某一特殊无人机机型开始了阵风问题和颤振主动控制的研究，应用现代控制理论对飞行器系统分别作开环和闭环分析，设计的控制律具有减缓阵风响应和抑制颤振的双重效果。M Tadi[4]研究了用于气动弹性系统中颤振抑制的反馈控制设计，推导了基于状态相关Riccati方程的反馈控制律。M Karpel[5]使用状态空间气动模型设计一个恒定增益的反馈控制系统，该系统可同时保证稳定性和完成对整个飞行包线内阵风响应参数的优化。多输入/多输出系统的气动弹性主动控制问题成为气动弹性分析的重要研究方面，吴志刚[6-7]团队以无人机二元机翼和带两个控制面板的三角机翼为研究对象，将滑模控制理论和LQC理论用于解决气动弹性主动控制。随着现代控制科学的发展，王囡囡等[8]提出了基于动柔度法的颤振主动控制研究，该方法无需提前知道机翼的刚度、阻尼等参数，可根据极点控制理论确定系统反馈控制增益。而真实的气动弹性控制系统是非线性的[9]，非线性系统更加复杂，求解难度更大，SH Moon等[10]基于非线性气动模型进行了最优控制设计的探索。A Behal等[11]研究了在不可压缩流场中的非线性二维机翼系统的自适应控制。丁千等[12]针对具有非线性俯仰刚度的二元机翼研究了颤振主动控制。考虑机翼俯仰方向阻尼和刚度存在非线性情况，许行之等[13]采用多项式非线性模型建立机翼控制模型，利用李雅普诺夫稳定性理论实现机翼的气动弹性自适应控制。

本文对机翼非线性主动控制进行了拓展研究。以二元三自由度机翼为研究对象，建立了机翼的非线性气动模型，得到时变控制系统。针对时变系统控制律设计困难问题，结合系统时变规律，设计了对应的状态反馈控制律，为解决非线性气动弹性控制问题提供了新思路。

1 三自由度二元机翼非线性气动模型

如图1所示，在机翼后缘有一控制面。系统的三自由度分别为刚心E的挠度h(向下为正)、机翼绕刚心的扭转角为α(迎风抬头为正)以及控制面偏转角β(向下偏转为正)。机翼的运动方程为：

(1)

式中：m为单位长度机翼的质量；Sα为单位展长机翼对弹性轴的质量静矩；Iα是单位展长机翼对弹性轴的质量惯性矩；Kh、Kα分别为机翼沉浮和俯仰刚度。机翼所受的升力L和力矩M可以表示为:

(2)

这里升力L和力矩M都由两个部分组成，Ll和Ml表示线性部分，表达式为：

(3)

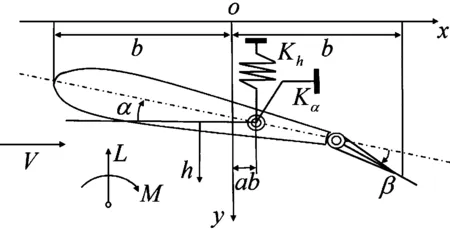
图1 三自由度二元机翼

Ln和Mn表示非线性部分，这里采用文献[14]中介绍的ONERA动态失速模型，表达式为：

(4)

需要说明的是，非线性气动系数下标z=L表示与升力有关系数；下标z=M表示与力矩有关的系数。非线性气动系数Cz表达式如下：

(5)

非线性气动力部分的有关参数有r1z，r2z，r3z为：

为简化计算，通常用折线代替静态空气动力曲线，如图2。

图2 静态空气动力曲线

(7)

为通过式(5)求解出非线性气动系数Cz，本文采用Laplace变换得方法，将式(5)进行Laplace变换并整理得：

(8)

通过Laplace逆变换可以得出：

(9)

分别令z=L和z=M代入式(4)并联立式(1)、式(2)、式(3)即可得到机翼的三自由度二元机翼非线性气动模型。

2 状态空间模型与控制律设计

把上一节得到的机翼非线性气动模型改写成状态空间形式：

(10)

图3 参数k2时间响应波形

针对系统的特征，将本文控制系统设计成状态反馈系统，K为反馈矩阵，系统矩阵变为(A-BK)，如图3所示，横坐标t=t+时，时变参数幅值为最大值，此状态对应的系统相关矩阵表示为A+、B和K+，横坐标t=t-时，时变参数幅值为最小值，此状态对应的系统相关矩阵表示为A-、B和K-，这两种状态结合李雅普诺夫判据可以得出：

(11)

定义折合系数ε，且ε∈(0,1)，将式(11)中两个不等式两边分别乘以系数ε和(1-ε)并相加，得到：

P([(1-ε)A-+εA+]-B[(1-ε)K-+εK+])<0

(12)

式(12)表示含有折合系数ε的新系统，且符合李雅普诺夫稳定性判据，此系统对应的相关矩阵可以表示为：

A(ε)=(1-ε)A-+εA+

(13)

K(ε)=(1-ε)K-+εK+

(14)

由于A+、A-、K-和K+为系统时变参数取最值对应的解，所以A(ε)、K(ε)可以表示出在整个时域范围内的系统所有满足李雅普诺夫稳定性判据的系统矩阵。任意时刻t0的状态反馈矩阵K(t0)求解过程如图4所示。

图4 反馈控制求解流程

图4说明了本文求解某一时刻反馈矩阵K(t0)具体步骤，由于直接运用解析法求解时变系统的反馈控制矩阵很难实现，本文采取建立时刻t0与折合系数ε的一一映射关系的方法来实现对K(t0)的求解。需要说明的是在运用式(11)求解K-和K+时，要借助线性矩阵不等式(LMI)工具箱，一个线性矩阵不等式问题一旦确定，就可以通过调用适当的线性矩阵不等式求解器来对这个问题进行数值计算。

整个机翼的状态反馈系统流程如图5所示，时变系统通过引入时钟信号实现对时变矩阵A(t)的表示，而后计算反解出折合系数ε，进而求出对应时刻的反馈矩阵K(t)，从而实现对系统的反馈控制。

图5 控制系统流程

3 算例仿真与分析

本研究选取的三自由度二元机翼模型的具体参数如表1。

表1 机翼模型参数

已知机翼的开环颤振速度为29.3 m/s，仿真时选取的空速为33.7 m/s(高于开环颤振速度的15%)，使用上一节设计的反馈控制系统，具体参数见附录，先仿真得到系统的开环时域响应，如图6所示。

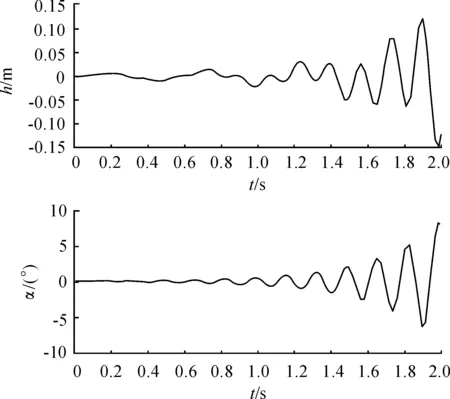
图6 开环时域响应

图6分别是机翼挠度和扭转角随时间的变化曲线，从仿真的结果可以看出，在开环系统条件下，风速为33.7 m/s时，此时风速高于机翼颤振速度，系统呈现振荡发散的状态。随后，接入反馈控制模块，在同样的风速下，仿真得到系统的闭环时域响应，如图7所示。

通过观察图7的机翼挠度和扭转角随时间的变化曲线，可以看出闭环控制系统是稳定的，系统在0.8s左右可以收敛至平衡位置，从而改善了机翼系统的气动弹性特性，提高了机翼安全飞行速度上限。当机翼受阵风干扰时，会因为外界干扰力作用而发生强迫运动，对机翼结构强度、疲劳以及飞行品质产生较大影响。这里主要讨论控制系统对阵风作用下机翼响应的影响。以“1-cos”阵风为例，因为实际工程中这类阵风遇到的频率最高，“1-cos”阵风速度表达式为：

(15)

其中：W0表示阵风峰值速度，取20 m/s；H表示离散尺度，取4 m。阵风的具体形式如图8所示。

图7 闭环时域响应

图8 “1-cos”阵风

分别计算开环系统和闭环系统在“1-cos”阵风影响下的机翼挠度响应，其中空速V=25 m/s，选取的空速低于机翼的颤振速度，也就是说此时机翼系统本身处于稳定状态，当遇到突风产生激励，机翼系统通过自身调节可以恢复稳定，得到的响应结果如图9所示。

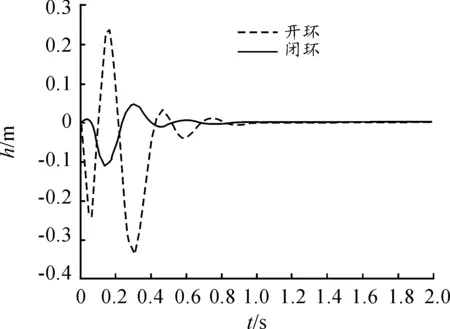
图9 机翼阵风响应结果

从图中对比开环系统和闭环系统的阵风响应，可以看出闭环控制系统相对于开环控制系统，有效降低了机翼振幅，同时缩短了机翼响应衰减时间，大大提高了机翼系统的稳定性，保证了机翼气动弹性特性和飞行品质。

4 结论

1) 针对时变系统控制律设计困难问题，结合系统时变规律，设计了对应的状态反馈控制律。

2) 通过仿真对比开环和闭环系统的超颤振速度条件下时域响应、阵风响应，表明设计的反馈控制律可以有效地改善机翼气动特性。