基于模糊动态故障树的提升机盘式制动系统可靠性研究

周广林，张继通，刘训涛，韩忠惠

(黑龙江科技大学 机械工程学院，黑龙江 哈尔滨 150022)

盘式制动系统是保证提升系统安全运行不可或缺的组成部分，是提升系统最关键安全保障装置之一，制动装置的可靠性直接关系到提升系统的安全运行可靠性[1-3]。随着矿用提升机提升量的不断增加，要求提升系统具有高可靠性、灵活性和安全性，所以，制动系统要具有高可靠性，是保证提升系统正常安全运行的必要条件。据统计，在矿井提升系统的故障中，由于制动系统失效导致的事故占60%以上[4]。

矿井提升机盘式制动系统结构复杂，在实际生产中对制动系统维护检修不当或系统本身制造存在的缺陷，都会给矿井提升系统正常运行带来很大影响，甚至造成事故，在实际生产中，盘式制动系统的故障现象、故障状态以及故障原因存在大量的随机性和动态性，考虑到系统的故障数据量较少、数据获取以及处理过程中存在大量的不确定性，采用传统的故障树分析不能针对系统失效的不确定性进行可靠性分析。

针对事件发生存在的动态性、随机性以及模糊性等特征，ZADEH[5]提出了模糊集理论处理不确定性问题。TANAKA等[6]提出采用梯形模糊数描述事件的故障概率。D.SINGER[7]在前人的基础上进一步研究了模糊故障树分析方法，将基本事件失效率用L-R型模糊数进行描述。李彦锋等[8]采用模糊动态故障树分析方法。黄洪钟等[9]运用模糊数理论结合动态故障树分析方法，给出了模糊重要度求解方法，对太阳翼驱动机构的故障问题进行了可靠性研究。王晓明等[10]基于连续时间贝叶斯网络的动态故障树分析方法，对具有动态特性的系统进行建模与评估，采用模糊数描述零部件基本的失效参数。杨玲[11]采用专家信心指数和三角模糊数修正方法获取底事件发生概率。高迎平等[12]在进行模糊动态故障树可靠性研究中，提出引入弱三角范数的概念，降低了由数据模糊性扩散导致计算结果不准确的问题。在矿山机械设备中对模糊动态故障树方面的研究成果较少，采用模糊动态故障树分析方法对盘式制动系统液压站的可靠性进行研究。

1 盘式制动系统液压站模糊动态故障树建模

1.1 盘式制动系统工作原理

矿井提升机盘式制动系统的作用主要包括工作制动、停车制动、安全制动、附加制动等。盘式制动系统主要包括盘式制动器(图1)和液压站(TE161型液压站如图2所示)。

图1 盘式制动器原理Fig.1 Schematic diagram of disc brake

液压站采用两套完全独立的电动机-变量柱塞泵及控制阀组，一套工作、一套备用[13]。盘式制动器对制动盘产生制动力矩，液压站控制和调节制动力矩。

图2 TE161液压站原理Fig.2 Schematic diagram of TE161 hydraulic station1—油箱;2—电加热器;3—温度传感器;4—吸油过滤器;5—电动机;6—变量柱塞泵;7—出油过滤器;8—比例溢流阀;9,13,23—电磁换向阀;10—溢流阀;11—单向节流截止阀;12—囊式蓄能器;14—电磁球阀;15—液动换向阀;16—单向阀;17—出口过滤器;18—球式截止阀;19—压力继电器;20—压力传感器;21—电接点电力表;22—远程调压阀;24—电接点温度计

1.2 盘式制动系统液压站动态故障树模型

在提升机制动系统中，通过大量的统计资料和理论分析，盘式制动系统出现的故障主要是制动器失效和液压系统失效两类故障，以及工人操作失误和电气故障[14]，盘式制动系统故障树模型，如图3所示。对盘式制动系统中的液压站的失效模块进一步构建动态故障树模型，如图4所示。

图3 盘式制动系统故障树Fig.3 Fault tree of disc brake system

图4 盘式制动系统的液压系统动态故障树Fig.4 DFT of hydraulic system of disc brake systemT—液压系统故障;M1—电磁换向阀故障;M2—电液比例调压装置故障;M3—液压站故障;M4—液动换向阀故障;M5—溢流阀故障;M6—比例溢流阀故障;M7—备用比列溢流阀故障;M8—液压站故障;M9—备用液压站故障;X1—电磁阀滑块变形;X2—电磁阀不换向;X3—电磁阀线圈短路;X4—比例放大器失效;X5—主阀芯上的阻尼孔堵塞;X6—导阀调整弹簧失效;X7—比例放大器失效;X8—主阀芯上的阻尼孔堵塞;X9—导阀调整弹簧失效;X10—电动机故障;X11—过滤装置故障;X12—恒压变量柱塞泵故障;X13—备用电动机故障;X14—过滤装置故障;X15—备用恒压变量柱塞泵;X16—弹簧失效;X17—滑阀磨损;X18—主阀芯上的阻尼孔堵塞;X19—导阀调整弹簧失效;X20—出口过滤器失效

2 盘式制动系统液压站模糊动态故障树的定量分析

2.1 定量分析理论

2.1.1 静态模块的分析

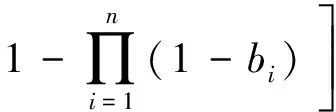
(1)

式中,n为三角模糊数的数量;mi为三角模糊数的均值;αi为三角模糊数的左半径值;βi为三角模糊数的左半径值。

(2)

2.1.2 动态模块的分析

(3)

图5 n种情况的模糊状态转移速率过程Fig.5 Fuzzy state transfer rate process for n species

(4)

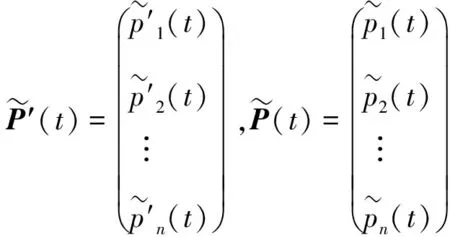
(5)

(6)

2.2 盘式制动系统液压站的动态故障树定量分析

通过对黑龙江龙煤矿业集团各分公司矿井提升机上使用的TE161型液压站进行调研，搜集统计各底事件失效数据，并进行综合统计分析，得到系统动态故障树各底事件的失效参数的均值，依据模糊数学中的扩增系数法，将各底事件精确均值的20%为模糊数的左右半径值，即α，β=0.2，作为对应的系统各个底事件的模糊故障参数，见表1。根据系统动态故障树底事件模糊失效参数，进行分析计算盘式制动系统液压站运行t=104h时的模糊故障概率。

对于静态子树M1,M5分别由3个底事件和2个底事件组成，且由或逻辑门连接，已知各个底事件的模糊失效率见表2，求运行时间为t=104h时的顶事件模糊故障概率。

表1系统动态故障树的底事件的模糊失效参数
Table1Fuzzyfailureparametersforthebottomeventofasystemdynamicfaulttree

代号模糊数/10-6X1[0.40 0.50 0.60]X2[0.64 0.80 0.96]X3[0.40 0.50 0.60]X4[0.16 0.20 0.24]X5[0.40 0.50 0.60]X6[0.08 0.10 0.12]X7[0.16 0.20 0.24]X8[0.40 0.50 0.60]X9[0.08 0.10 0.12]X10[0.40 0.50 0.60]X11[0.04 0.05 0.06]X12[0.24 0.30 0.36]X13[0.40 0.50 0.60]X14[0.04 0.05 0.06]X15[0.24 0.30 0.36]X16[0.40 0.50 0.60]X17[0.32 0.40 0.48]X18[0.40 0.50 0.60]X19[0.32 0.40 0.48]X20[0.32 0.40 0.48]

表2静态子树M1,M5事件及其模糊参数
Table2StaticsubtreeM1,M5eventsandtheirfuzzyparameters

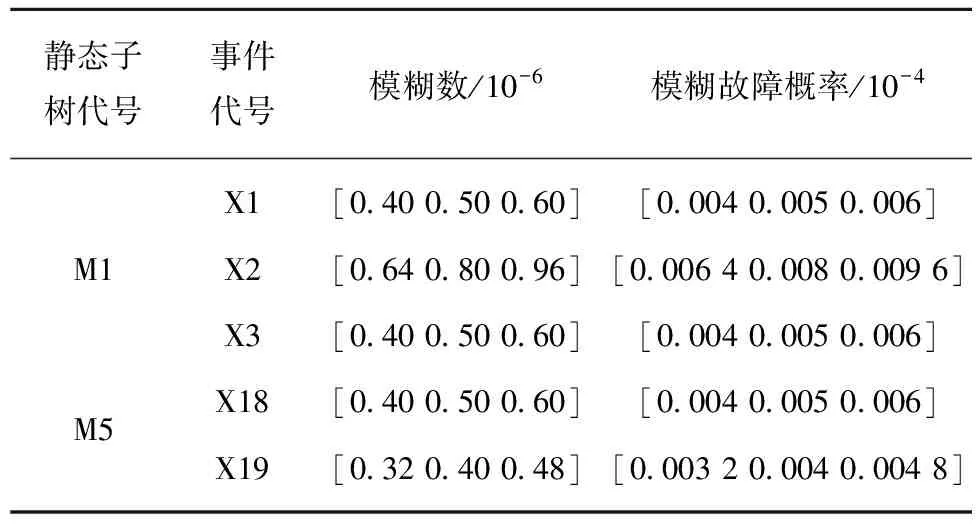
静态子树代号事件代号模糊数/10-6模糊故障概率/10-4X1[0.40 0.50 0.60][0.004 0.005 0.006]M1X2[0.64 0.80 0.96][0.006 4 0.008 0.009 6]X3[0.40 0.50 0.60][0.004 0.005 0.006]M5X18[0.40 0.50 0.60][0.004 0.005 0.006]X19[0.32 0.40 0.48][0.003 2 0.004 0.004 8]

根据或逻辑门的模糊概率计算式(1)，将底事件的模糊故障概率代入，得到M1顶事件的模糊故障概率分别为[1.43×10-2，1.79×10-2，2.14×10-2]，M5的顶事件的模糊故障概率分别为[0.72×10-2，0.9×10-2，1.08×10-2]。

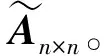
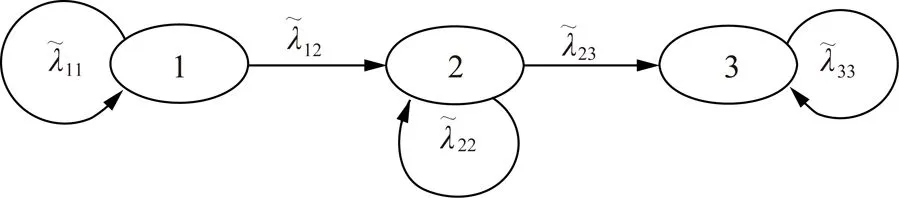
图6 动态子树M2,M3的糊状态转移速率Fig.6 Transfer rate diagram of fuzzy state of dynamic subtree M2 and M3

根据式(4)，得到微分方程组为

(7)

(8)

(9)

(λ11=λ22)

(10)

根据表1中，M2底事件的模糊失效率参数[0.64×10-6,0.77×10-6,0.96×10-6]，M3底事件的模糊失效率参数[0.68×10-6,0.83×10-6,1.02×10-6]，代入式(10)，求解得到动态子树M2顶事件的模糊故障概率为[2.04×10-5,2.95×10-5,4.56×10-5]，M3顶事件的模糊故障概率为[2.31×10-5,3.43×10-5,5.17×10-5]。

对动态子树M4，首先，其逻辑关系由优先与门连接底事件和顶事件，已知底事件X18,X19的模糊失效率分别为[0.40×10-6,0.50×10-6,0.60×10-6]、[0.32×10-6,0.40×10-6,0.48×10-6]，根据动态故障树对M4定量分析的计算公式，得到M4顶事件的模糊故障概率[1.83×10-5,2.15×10-5,2.62×10-5]。

通过对静态子树和动态子树的模糊定量分析，得到各个子树的模糊故障概率，根据或门计算式(1)，得到模糊故障概率对应不同截集水平λ所对应的置信区间见表3，其隶属度函数，如图7所示，从图7可以看出，得到系统运行t=104h时，系统故障可靠性最小值是0.025;最大值是0.037;系统最可能故障的概率是0.031。

表3系统顶事件故障概率的置信区间
Table3Confidenceintervalforthefailureprobabilityofthetopevent

λamb00.024 80.0310.037 20.10.025 40.0310.036 60.20.026 00.0310.036 00.30.026 70.0310.035 30.40.027 30.0310.034 70.50.027 90.0310.034 10.60.028 50.0310.033 50.70.029 10.0310.032 90.80.029 80.0310.032 20.90.030 40.0310.031 61.00.031 00.0310.031 0

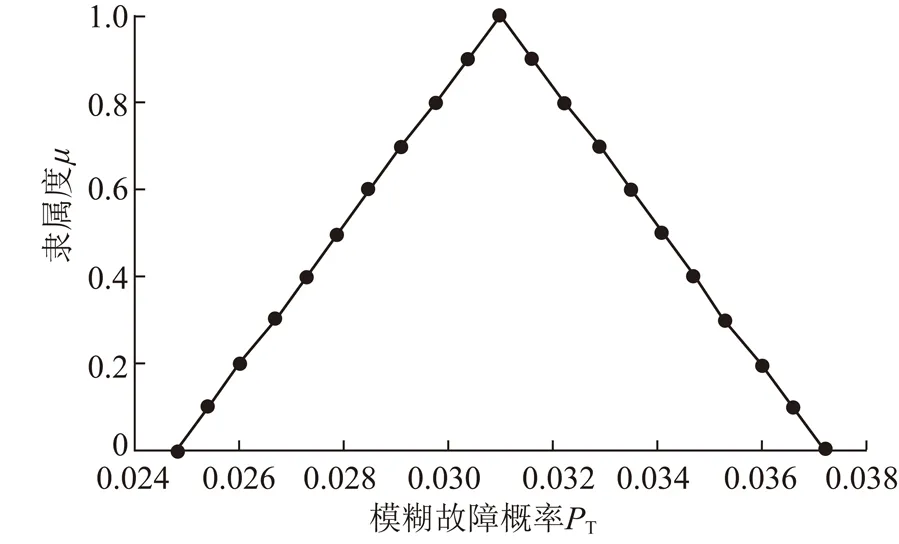
图7 t=104 h时系统动态故障树的顶事件模糊故障概率Fig.7 Fuzzy fault probability of the top event of the system dynamic fault tree at t=104 h

2.3 模糊概率重要度分析

在对系统模糊动态故障树进行定量分析时，主要是求解系统顶事件的模糊故障概率。为了进一步反映出各个底事件在系统中的重要程度，结合模糊数学知识和概率重要度知识，用模糊概率重要度来衡量，如式(11)所示[9]。

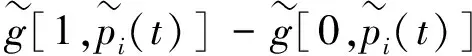
(11)

动态故障树中包含静态逻辑门和动态逻辑门，由模糊概率重要度的定义公式，推导得到“或”门、冷备份门的底事件模糊重要度的求解公式。

“或”逻辑门中底事件的模糊重要度公式:

αj)-αjλ],1-mj,1-[(mj+βj)+βjλ]}

(12)

冷备份门中底事件的模糊重要度公式:

(13)

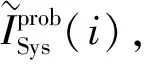
(14)

分别对静态子树和动态子树求解底事件的模糊重要度。首先，对静态子树中的底事件求解，静态子树M1，M5是“或”逻辑门，根据“或”逻辑门中底事件的模糊重要度式(12)，求解结果见表4。

表4底事件的模糊概率重要度
Table4Importanceofthefuzzyprobabilityofthebottomevent

代号故障概率概率重要度M22.95×10-5[0.963 9 0.969 9 0.975 9]M33.43×10-5[0.963 9 0.969 9 0.975 9]X10.49×10-2[0.969 6 0.974 7 0.979 8]X20.79×10-2[0.973 1 0.977 6 0.982 1]X30.49×10-2[0.969 6 0.974 7 0.979 8]M42.00×10-5[0.963 9 0.969 9 0.975 9]X180.49×10-2[0.969 6 0.974 7 0.979 8]X190.39×10-2[0.972 8 0.977 3 0.981 8]X200.39×10-2[0.972 8 0.977 3 0.981 8]

进一步求解得到所有底事件的模糊概率重要度见表5，通过对表5分析，对故障概率和重要度进行排序，在盘式制动系统液压站中，电磁换向阀、出口过滤器是系统的关键部位，一旦失效，导致整个系统就出现故障，所以，选用的该部件应该具有高可靠性能，并且在日常检修过程中重点检查，过滤器也是重要检查的部位，保证液压系统液压油的质量。

表5系统动态故障树各个底事件模糊概率重要度
Table5Importanceoffuzzyprobabilityforeachbottomeventofasystemdynamicfaulttree

代号概率重要度排序X1[0.969 6 0.974 7 0.979 8]3X2[0.973 1 0.977 6 0.982 1]1X3[0.969 6 0.974 7 0.979 8]3X4[0.956 9 0.964 1 0.971 2]6X5[0.962 6 0.968 9 0.975 1]4X6[0.960 2 0.966 9 0.973 5]5X7[0.956 9 0.964 1 0.971 2]6X8[0.962 6 0.968 9 0.975 1]4X9[0.960 2 0.966 9 0.973 5]5X10[0.954 5 0.962 1 0.969 6]7X11[0.954 5 0.962 1 0.969 6]7X12[0.952 2 0.960 2 0.968 1]8X13[0.954 5 0.962 1 0.969 6]7X14[0.954 5 0.962 1 0.969 6]7X15[0.952 2 0.960 2 0.968 1]8X16[0.264 2 0.386 9 0.509 5]10X17[0.370 3 0.475 3 0.580 2]9X18[0.969 6 0.974 7 0.979 8]3X19[0.972 8 0.977 3 0.981 8]2X20[0.972 8 0.977 3 0.981 8]2

3 结 论

(1)采用模糊动态故障树分析方法，结合模糊理论，给出了静态模块和动态模模块以及模糊概率重要度求解方法。

(2)TE161液压站采用冗余系统设计，在故障分析过程中存在模糊性、不确定性等特点，构建了模糊动态故障树模型，采用三角模糊数描述盘式制动系统液压站各个底事件的故障率，并结合截集λ水平和扩张原理，得到系统运行t=104h时，系统故障可靠性最小值是0.025;最大值是0.037;系统最可能故障的概率是0.031。

(3)求解了盘式制动系统液压站各个底事件的模糊概率重要度，对底事件的模糊概率重要度进行排序分析，寻找到了故障率高的部位，为液压站改进提供借鉴。