基于密度的全局K-means算法的改进
徐 娟,范 菁,陈楚天,曲金帅1,
(1. 云南民族大学 云南省高校信息与通信安全灾备重点实验室,云南 昆明 650500; 2. 云南民族大学 电气信息工程学院,云南 昆明 650500)
传统的K-means算法,方法简单有效,收敛迅速,便于处理较大型数据,已经被广泛运用到各个领域[1].但是传统的K-means算法对初始中心点[2]的选择依赖性强,为了解决该问题,人们提出了很多增量式算法[3].
2003年Likas[4]等提出了一种全局K-means聚类算法,同时在文献中还提出了一种改进的快速全局K-means算法.全局K-means聚类算法是一种增量式算法,该算法需要通过全局搜索来确定下一个簇的初始聚类中心点,每次都需要迭代运行N次(N是数据集中数据的个数)K-means算法计算簇内平方误差函数E,使得簇内平方误差函数最小的点,则设定为下一簇的最佳初始中心点.该算法的缺点是每一次都需要迭代N次,计算量大,在处理大数据集时消耗的时间更多,因此文献[4]提出了改进的快速全局K-means聚类算法,该算法提出了一种新的簇内中心判断指标参数bi替换全局K-means算法的簇内平方误差函数E,减少了算法的计算量.
1 K-means算法
传统K-means算法的规则:从原始数据中随机选取K个初始聚类簇中心点,然后按照数据的最短距离点的原则(欧式距离),将原始数据集中的点分配给最近的簇中心.分配完所有的数据点后,在每个已生成的簇中,计算簇中点集的质心点,以所有数据的平均值点作为新的聚类簇中心点.重复迭代计算,直到簇中心点位置收敛,收敛的判断方式一般采用簇内误差平方和函数.此时可判断为最佳聚类中心点,进行最后的聚类,聚类结束[5].具体流程如下:
Step 1 初始化:从待聚类的数据集中随机选择k个聚类中心点,c1c2...ck.
Step 2 计算除聚类中心点外其他的数据到这k个簇中心点的距离,并将该数据分配到距离最近的簇中.
Step 3 计算簇中点集的质心点,质心点定义为所有数据点的均值点,再次确定k个簇的聚类中心,并根据误差平方和公式计算相应的评价函数值.
Step 4 当2次的评价函数值之差小于ε(ε是一个人为定义的数值),或者到达设定的最大迭代次数,可以认为算法收敛,此时算法停止.否则转步骤2.
2 全局K-means聚类算法
全局K-means聚类算法[5]用一种递增式的方法来选择一个新的簇的最佳初始聚类中心.具体过程如下:
将一组数据集X={x1,x2,...,xn},xi∈RD(i=1,2,...,N),分为k个簇,聚类中心分别为(c1,c2...,ck),形成的聚类簇为(M1,M2,...Mk).

Step 2 终止条件:k=k+1;若k>K,初始中心点的选择结束.
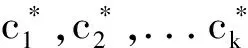
3 快速全局K-means聚类算法
快速全局K-means聚类算法,在不影响聚类效果的前提下,大大的减少了全局K-means聚类算法的算法耗时.它的改进之处在于,定义了一个新的参数bi代替了簇内平方误差和函数E,通过减少算法的计算量来提高聚类速度.
(1)
其中,bi表示的是相比较数据集中的其他点,xi作为簇内中心点时,得到的簇内平方和的差值.该差值越大,表示对应的E值越小.该算法流程与全局K-means聚类算法基本一致,只需将选择下一簇内初始中心点的条件换为bi值,选取使bi值最大的点作为下个簇的初始中心点.
4 改进的DGK-means算法
针对全局K-means聚类算法和快速全局K-means聚类算法在选择下一簇的聚类中心点时,需要对数据集中所有的数据点逐一计算E值并进行对比,这一过程中存在很多不可能作为备选点的数据点,比如数据集的边缘孤立点,数据中的噪声点等.对于这些噪声点的计算属于无用功,反而增加了算法的计算量.基于此问题,提出了一种基于高密度数[6-7]的全局K-means聚类算法.
该算法旨在将N个数据点依靠其各个点的密度数分类,将高密度数的数据点提取出来,同时剔除低密度点.剔除的低密度点即是该数据集中相对的离散点.将高密度数的数据聚集形成新的数据集合Data1.该部分也提出了一个依据密度级来确定聚类个数的想法,依靠密度等级的划分将该数据集划分成相应个数的聚类簇.
密度数:点在其邻域范围R内点的个数.
Density(xi)={P∈X|dist(xi,p)≤R}.
(2)
改进流程图:

5 实验仿真
本实验仿真选用了UCI数据库中的4个数据集进行实验对比,证明了本文所提出的DGK-means聚类算法,比全局K-means算法和快速全局K-means算法,聚类耗时更短[8-9].并且选择了分类适确性指标(davis-bouldin idex,DB),简称为DB值,来衡量聚类效果.DB值用来衡量簇内和簇间的关系.DB值越小,意味着簇内数据之间的距离越小,相互联系度高,还表示簇间的距离越大,聚类结果越好.
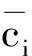
(3)
本实验采取了4组从UCI数据库中下载的数据集,见表1.对每一组数据用3种聚类算法分别运行20次,并求得均值时间作比较.同时计算每一个算法的DB值,来衡量算法的稳定性,判断聚类效果的优劣.

表1 数据集
图2为IRis数据的高密度数点集,图3为本文所提的DGK-means算法对IRIS数据集的聚类结果图,图4为GK-means,FGK-means,和DGK-means算法针对Iris数据集,运行所需时间的对比图.取20次运行时间的均值做对比如表2所示,本文所提的DGK-means算法用时分别近似于全局K-means算法和快速全局K-means算法的51.64%和71.68%.同时本文所提的改进算法的DB值与其他2种算法相比,差距较小,可以保证聚类效果的一致性.


表2 3种算法对Iris数据集的运行时间s
图5为Imports-85数据集的高密度数点集,图6为本文所提的DGK-means算法对Imports-85数据集的聚类结果图,图7为GK-means,FGK-means,和DGK-means算法针对Imports-85数据集,运行所需时间的对比图.取20次运行时间的均值做对比如表3所示,本文所提的DGK-means算法用时分别近似于全局K-means算法和快速全局K-means算法的34.7%和56.34%.
图8为WDBC数据的高密度数点集,图9为本文所提的DGK-means算法对WDBC数据集的聚类结果图,图10为GK-means,FGK-means,和DGK-means算法针对WDBC数据集,运行所需时间的对比图.取20次运行时间的均值做对比如表4所示,本文所提的DGK-means算法用时分别近似于全局K-means算法和快速全局K-means算法的15.08%和30.94%.



表3 3种算法对Imports-85数据集的运行时间s

表4 3种算法对WDBC数据集的运行时间 s
图11为Mice protein expression Data Set数据的高密度数点集,图12为本文所提的DGK-means算法对Mice protein expression Data Set的聚类结果图,图13为GK-means,FGK-means,和DGK-means算法针对Mice protein expression Data Set数据集,运行所需时间的对比图.取20次运行时间的均值做对比如表5所示,本文所提的DGK-means算法用时分别近似于全局K-means算法和快速全局K-means算法的13.98%和29.4%.


表5 3种算法对Mice protein expression Data Set的运行时间 s
综上分析,在不影响最终聚类效果的前提下,本文所提出的DGK-means算法,对比全局K-means算法和快速全局K-means算法,有效地减少了算法的运行时间.
6 结语
本文在学习全局K-means聚类算法的过程中,提出了一种缩小备选数据点的改进算法DGK-means聚类算法.该方法通过定义高密度数的概念,缩小了作为备选的下一簇的初始中心点点集,减少了算法的迭代计算次数.通过UCI 机器学习数据库的4组数据测试, 验证了本文提出的DGK-means算法在保持聚类效果稳定的情况下,聚类用时少于全局K-均值聚类算法和快速全局K-均值聚类算法,提高了算法的聚类效率.

