超高速碰撞2A12铝板产生的热辐射演化特征实验研究

韩雅菲， 唐恩凌， 郭 凯， 贺丽萍

(沈阳理工大学 装备工程学院， 辽宁 沈阳 110159)

1 引 言

超高速碰撞产生的热辐射是超高速碰撞过程中的重要物理现象，通过分析超高速碰撞产生的热辐射特征可以获得初始碰撞条件、弹靶材料组分及碰撞造成的毁伤程度等信息。因此，研究超高速碰撞产生的热辐射效应在天体物理、深空探测以及空间碎片感知等方面具有重要的应用价值[1-3]。

目前国内外科研人员对超高速碰撞产生热辐射特征的研究主要采用光电二级管、光谱仪等测量仪器将闪光信号转换为电信号，通过理论计算获得闪光辐射特征各物理量。Carolyn[4]用硅硼玻璃弹丸撞击浮石粉来模拟月球表面的撞击事件，采用高速光电二极管测量了闪光辐射强度，发现不同波长的闪光辐射强度整体演化趋势一致；Baird[5]从理论上推导了闪光辐射强度与碰撞速度的关系；进一步地，Goel[6]采用球状铁弹丸撞击钨、铜、太阳能电池等7种不同靶材模拟微流星体对航天器的撞击，得到了闪光辐射强度与质量和速度的关系式；Thornhill[7]研究小组将钛飞片加速至11 km/s撞击铝板，测量得到闪光辐射温度范围在1 500～2 500 K之间；而Collette[8]采用粒子加速器将铁微粒加速到1～32 km/s撞击钨目标，得到了闪光辐射温度在2 500～5 000 K之间；Reinhart[9]测量了不同冲击压力下的闪光辐射温度；Thomas[10]和Jaime[11]则对高速撞击产生的闪光轮廓演化特征进行了研究。

在国内，石安华等[12]采用PIN型光电二极管测量了LY12铝球撞击LY12铝板及铜板产生的波长为574 nm和672.7 nm的光谱辐射强度，证明了撞击铜板产生的光谱辐射强度远大于撞击铝板产生的光谱辐射强度。唐恩凌[13-16]研究小组通过大量的实验结果拟合得到了闪光辐射强度与碰撞速度的关系，并建立了碰撞点附近最大闪光辐射强度及温度的空间演化模型，验证了碰撞产生的闪光辐射强度以近似椭球的形状向外膨胀。

现有的研究成果主要侧重于对超高速碰撞产生的闪光辐射强度及温度的讨论，而对于其他热辐射特征物理量的研究甚少；尤其对于金属材料碰撞产生的热辐射特征研究鲜见报道。为进一步明确超高速碰撞产生热辐射效应的物理过程，本文利用自行构建的超高速碰撞产生热辐射测量系统开展了不同碰撞角度下铝弹丸以超高速碰撞铝板产生热辐射的实验研究，得到了闪光辐射强度、闪光辐射温度、辐射能量、辐射源面积以及发光效率的演化过程，综合分析超高速碰撞诱发的热辐射演化特征并揭示了碰撞角度与热辐射演化特征各物理量的关联规律。

2 热辐射演化特征物理量

2.1 闪光谱辐射强度

当物体的温度高于绝对零度时会向周围空间发出热辐射，辐射能与温度及波长有关。在热辐射平衡的条件下，辐射能与波长、温度的关系满足普朗克热定律，即单位面积黑体(发射率ε=0)在半球方向、单位时间、单位波长范围内向半球空间辐射的能量即光谱的单色辐射强度满足

式中：C1为第一辐射常数，3.742×10-16W·m2；C2为第二辐射常数，1.4388×10-2W·K；λ为波长，m；T为黑体辐射温度，K。考虑实际物体(灰体)的表面发射率ε(0<ε<1)，则在可见光范围(380 nm<λ<780 nm)内灰体特定波长的光谱辐射强度即闪光辐射强度Iλ为:

λ∈(380 nm,780 nm).

(2)

2.2 闪光谱辐射温度

在可见光范围内，选取4个波长λ1、λ2、λ3、λ4的闪光辐射强度I1、I2、I3、I4，依据公式(2)，同时假定不同波长对应的材料发射率相同，即ε1=ε2=ε3=ε4，建立有关闪光辐射温度的拟合目标函数G(T)，得到闪光辐射温度T与波长及闪光辐射强度的关系式[17]

(3)

2.3 辐射能量与辐射源面积

辐射源面积是指物体发射辐射能区域的表面积。由Stephen-Bolzman定律，单位时间内黑体的单位表面积向半球空间辐射的全波长能量Eb与辐射温度T的四次方成正比:

(4)

其中：σ为Stephen-Bolzman常数，σ=5.67×10-8W/(m2·K4)。若实际物体的辐射源面积为As，光谱辐射强度为Iλ，闪光辐射温度为T，则辐射源面积As与热辐射各物理量满足[5]

对于实际物体(灰体)在可见光范围内辐射能量的计算，需考虑发射率并在可见光波长范围内积分。

2.4 发光效率

在可见光范围内，实际物体在闪光持续时间范围内的闪光辐射总能量E定义为:

(6)

则发光效率η为闪光辐射总能量与初始动能的比值:

(7)

其中：m为弹丸质量，kg；v为弹丸碰撞速度，km/s。

3 实验测量

3.1 测量系统

超高速碰撞产生的热辐射测量系统主要由二级轻气炮、多通道瞬态光纤高温计、太阳光模拟器(用于标定)及示波器组成。采用二级轻气炮加载弹丸，通过调整一二级气室气压及改变靶板角度，实现弹丸以不同入射速度及入射角度撞击靶板；磁测速装置用于测量碰撞速度；真空泵将发射管和靶舱抽真空以消除气体对实验测量过程的影响；光纤探头放置于碰撞点正上方，与瞬态光纤高温计相连接。当碰撞闪光信号出现在光纤探头的锥体探测区域时，闪光信号经瞬态光纤高温计中的光电倍增管转换成电信号由示波器读出；触发系统与瞬态光纤高温计及示波器连接，确保实验数据测量的同步性。

图1 超高速碰撞产生热辐射的演化特征测量系统

多通道瞬态光纤高温计(型号FOP-8)的温度测量范围为20～10 000 K，实验选用400,500,600,700 nm四个通道进行同步测量。

3.2 实验标定

碰撞闪光信号采集前，采用太阳光模拟器作为标准光源对测量闪光电压信号进行标定。将光纤探头置于太阳光模拟器距离光源Ic处，标准光经过高温计中的光电倍增管转换成电信号，记录标定电压hc和标定负载电阻Rc。标准光源的光谱辐射照度Nr(λ)由中国测量技术研究院标定给出，波长400,500,600,700 nm对应的光谱辐射照度Nr(λ)为281.7，235.5，357.3，280.7 μW/(nm·cm2)。

测量闪光辐射强度时，将光纤探头置于与靶板垂直并与碰撞点距离为lexp处，记录实验负载电阻Rexp和hexp示波器测得闪光电压值hexp，已知光纤孔径角为α，则闪光辐射强度测量值Iexp为：

(8)

3.3 实验参数

实验中光纤探头与碰撞点距离为60 mm；弹丸为球形铝弹，直径4.6 mm，质量0.145 g；靶板材料为2A12铝，几何尺寸为长×宽×厚=120 mm×120 mm×20 mm，经测定其发射率为0.1(波长为500 nm时)；光纤孔径角为α=37°，靶室真空度为100 Pa。表1为实验基本参数及高温计标定值。

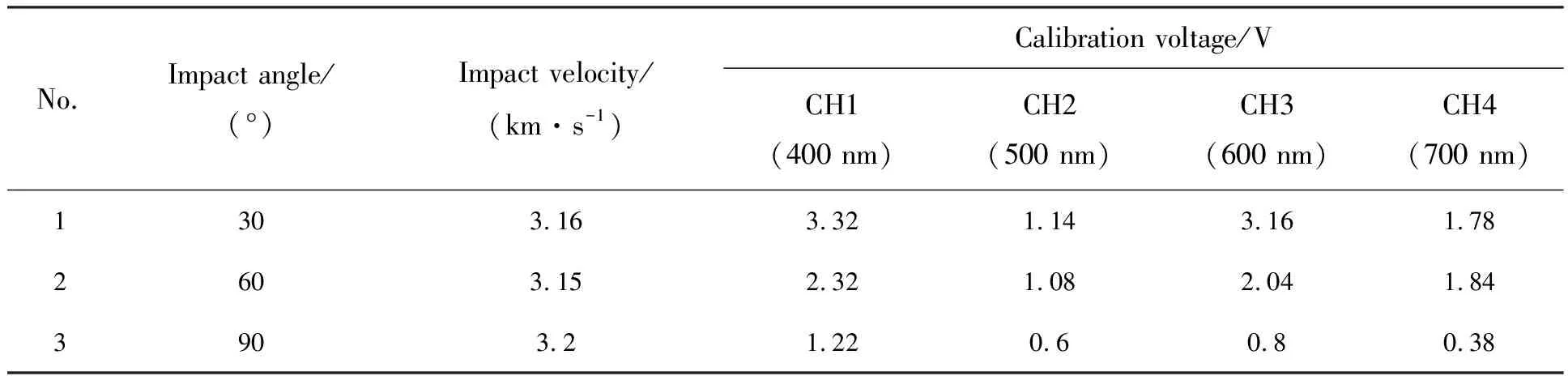
表1 实验基本参数及高温计标定值

4 实验结果及分析

4.1 闪光辐射强度、辐射温度演化过程

通过实验测量得到了铝弹丸以相近碰撞速度、不同碰撞角度碰撞铝靶产生的闪光辐射强度、闪光辐射温度演化时程曲线。由测量的闪光电压值hexp依据公式(8)计算得到闪光辐射强度，由不同波长对应的闪光辐射强度依据公式(3)计算得到闪光辐射温度。图2为No.1、No.2、No.3实验中四通道波长对应的闪光辐射强度演化时程曲线；图3为No.1、No.2、No.3实验中最强闪光辐射强度对应波长的时程曲线；图4为No.1、No.2、No.3实验不同碰撞角度下的闪光辐射温度时程曲线，实验记录时间为触发后40 μs。

由图2、图3闪光辐射强度演化曲线可以得出：No.1、No.2、No.3实验中不同波长对应的闪光辐射强度整体演化趋势相同，均呈现快速上升缓慢衰减的特征；随着碰撞角度的增加，闪光辐射强度峰值降低。由图3闪光辐射强度演化曲线经过平滑处理后得到30°、60°、90°碰撞角度下闪光辐射强度达到峰值所需时间分别为1.9,7,13.8 μs，衰减到1/2峰值所需时间分别为5.5,12.6,27.9 μs。

图2 不同入射角度及波长对应的闪光辐射强度演化曲线。(a)30°;(b)60°;(c)90°。

图3 不同入射角度下的闪光辐射强度最大值演化曲线

Fig.3 Evolutionary curves of maximum flash radiant intensity with different incident angles

因此，碰撞角度越大，闪光辐射强度达到峰值所需时间越长，衰减过程越缓慢。闪光辐射温度的演化趋势与闪光辐射强度基本相同。

由维恩位移定律：闪光辐射强度最大值对应波长与温度的乘积为一常数，即：λmT=2.8976×10-3m·K。因此，闪光辐射温度越高，闪光辐射强度最大值对应的波长越短。由图2、图3所示结果：当碰撞角度为30°时闪光辐射温度最高，闪光辐射强度最大值对应的波长为400 nm；当碰撞角度为90°时闪光辐射温度最低，闪光辐射强度最大值对应的波长为700 nm。实验结果基本符合维恩位移定律。

当弹丸与靶板碰撞时，在碰撞点附近弹靶材料受到剧烈的冲击压缩瞬间融化并在拉伸波的作用下向外喷溅。当弹丸垂直碰撞靶板时，由于弹丸的阻挡只有少量的喷溅物喷出并产生闪光；而当弹丸倾斜碰撞(小于90°)靶板时，产生的大量喷溅物沿下弹道方向瞬间喷出。因此，碰撞角度越小，闪光辐射温度越高，到达峰值的时间越短。同时，由于超高速碰撞产生的闪光呈现溅射发光的特征，因此闪光辐射强度及闪光辐射温度曲线出现多次尖峰(图4)。

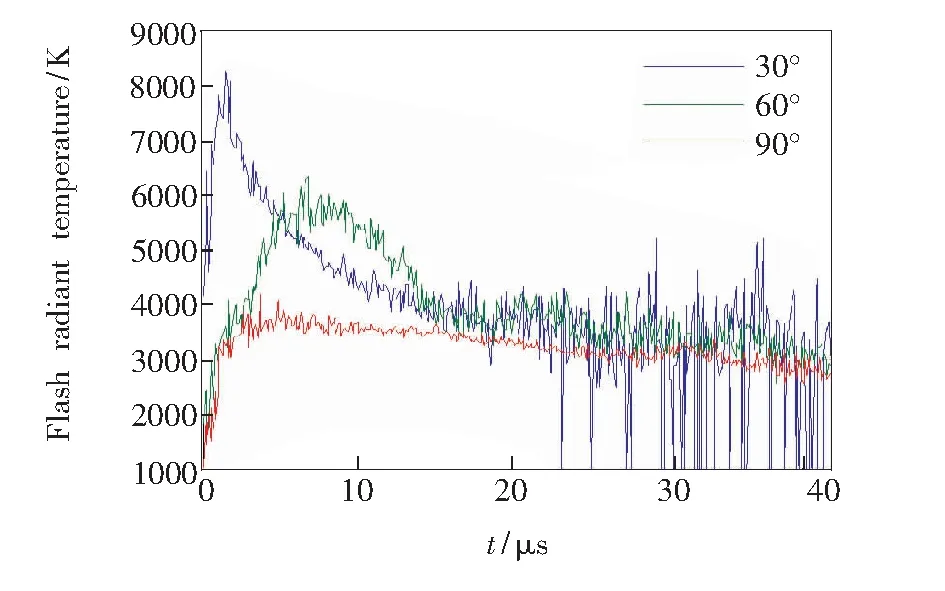
图4 不同碰撞角度下的闪光辐射温度演化曲线

Fig.4 Evolutionary curves of flash radiant temperature with different impact angles

4.2 闪光辐射能量演化过程

对光谱辐射能量计算采用近似的方法，由测量得到400,500,600,700 nm波长对应的闪光辐射强度值分别为I1、I2、I3、I4，将380～480 nm范围内波长对应的闪光辐射强度近似为I1，480～580 nm范围内波长对应的闪光辐射强度近似为I2，580～680 nm范围内波长对应的闪光辐射强度近似为I3，680～780 nm范围内波长对应的闪光辐射强度近似为I4。

由材料的发射率依据公式(4)计算得到光谱辐射能量。图5为单位面积(m2)不同碰撞角度条件下全谱及可见光范围的光谱辐射能量理论值；图6为不同碰撞角度条件下可见光与全谱的光谱辐射能量的比值。结果表明：光谱辐射能量的演化过程与闪光辐射温度基本相同；可见光范围内的光谱辐射能量占全谱辐射能量的比值随温度的升高而增加。

图7为由闪光辐射强度计算得到的实际辐射面积范围内闪光辐射能量的测量值。由于实际的辐射源面积远远小于单位面积(m2)，因此实验得到的闪光辐射能量小于单位辐射面积闪光辐射能量的理论计算结果。

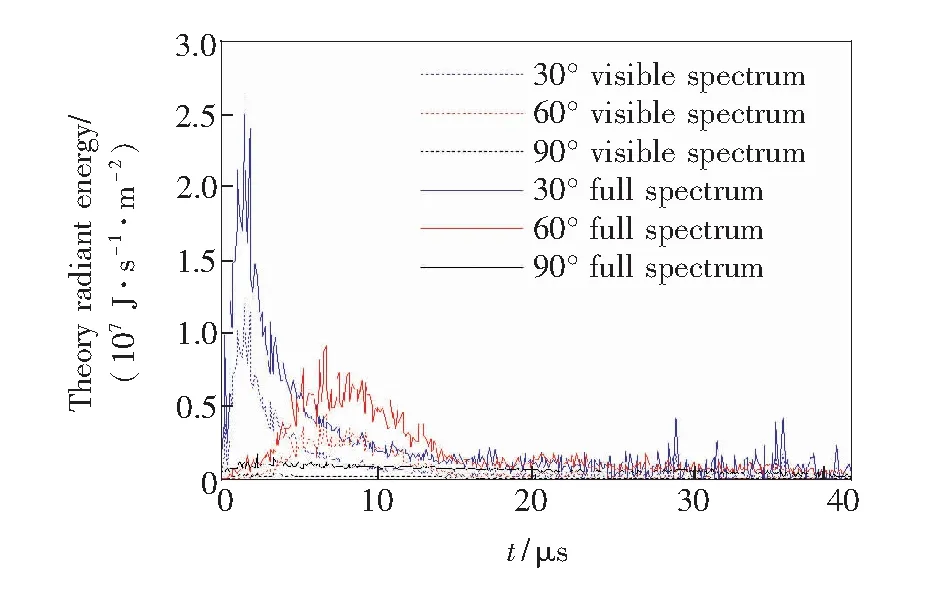
图5 不同碰撞角度下的全谱及可见光谱辐射能量理论值

Fig.5 Theoretical values of radiatiant energy of full spectra and visible spectra with different impact angles

图6 不同碰撞角度下可见光与全谱辐射能量的比值

Fig.6 Ratio of radiatiant energy of visible spectra and full spectra and with different impact angles

图7 不同碰撞角度下的可见光谱辐射能量测量值

Fig.7 Measured values of visible spectral radiatiant energy with different impact angles

4.3 辐射源面积演化过程

假定在碰撞闪光的过程中，辐射源面积始终不变，依据Stephen-Bolzman定律，闪光辐射温度与闪光辐射能量的演化趋势完全相同，而实际情况并非如此，因此辐射源面积是随时间不断变化的量。依据公式(5)由闪光辐射能量的测量值和单位辐射面积闪光辐射能量的理论计算结果估算辐射源面积，结果如图8所示。图9是碰撞角度为30°时闪光辐射温度与辐射源面积的演化曲线对比图。

图8 不同碰撞角度下的辐射源面积演化曲线

Fig.8 Evolutionary curves of radiant source area with different impact angles

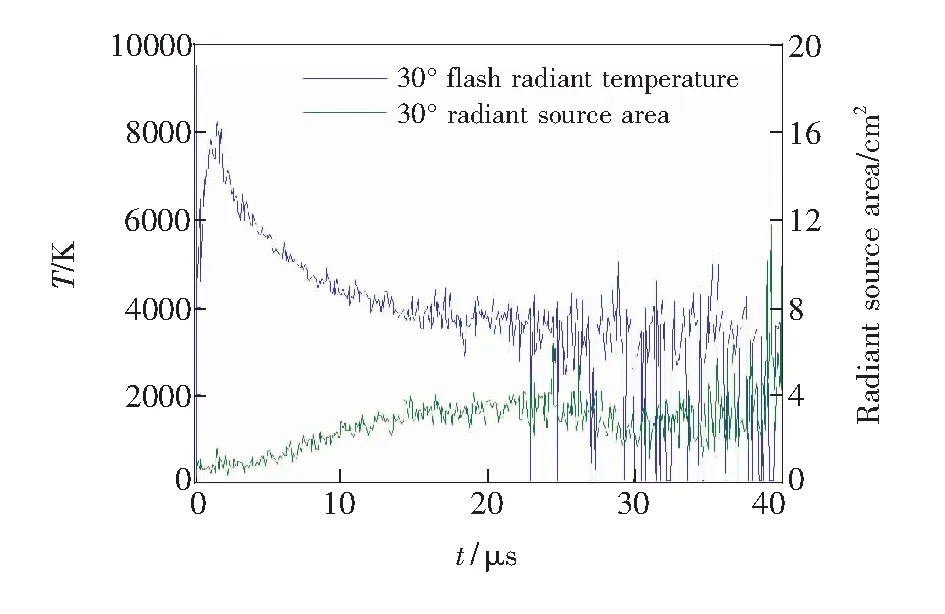
图9 30°碰撞角度下闪光辐射温度及辐射源面积演化曲线

Fig.9 Evolutionary curves of flash radiant temperature and radiant source area with 30° impact angle

弹丸与靶板碰撞的瞬间，弹丸的动能转化成材料的内能使部分材料气化；弹丸的入射角度越小，弹丸与靶板的摩擦面积越大，产生的摩擦剪切热越高，辐射源面积越大(图8)；同时，强冲击波向四周传播使辐射源面积不断增加。不同于闪光辐射温度的演化过程，辐射源面积在闪光辐射温度达到峰值后继续缓慢增加，随着弹靶碰撞产生的冲击波在靶板中多次反射能量不断衰减，辐射源面积达到峰值后缓慢减小(图9)。

4.4 发光效率演化过程

图10为不同碰撞角度下的发光效率演化曲线。发光效率随闪光辐射能量的增加而增加，并逐渐趋于稳定。同样，弹丸的入射角度越小，弹靶产生的摩擦剪切热越高，铝原子吸收能量使核外电子跃迁并释放光子的几率越高，由此，发光效率随入射角度的减小而增加。

图10 不同碰撞角度下的发光效率演化曲线

Fig.10 Evolutionary curves of luminous efficiency with different impact angles

由实验结果可知：在测量时间范围内碰撞角度为30°时发光效率最大值为2.13×10-5，碰撞角度为90°时发光效率最大值为1.09×10-5。Carolyn[18]对不同孔隙率材料的发光效率进行了研究，分别对孔隙率为43%的压实浮石粉和孔隙率为90%的珍珠岩的发光效率进行了测定，结果表明发光效率的数量级由10-5降至10-6，并得出了材料的孔隙率越大发光效率越低的结论。本文实验中采用的2A12铝孔隙率极低，发光效率数量级为10-5，与文献[18]实验结果在同一数量级。

4 结 论

通过对相近碰撞速度、不同碰撞角度下铝弹丸超高速碰撞铝板产生的热辐射相关物理量的测量及计算，得到如下结论：

(1)相同碰撞条件下，不同波长对应的闪光辐射强度演化趋势基本相同；相近碰撞速度、不同碰撞角度条件下闪光辐射强度与闪光辐射温度的演化过程均呈现急剧上升达到峰值后缓慢衰减的特征；同时，随着碰撞角度的增加，闪光辐射强度及闪光辐射温度的峰值降低，二者达到峰值及衰减所需的时间增加。

(2)可见光谱辐射能量与全谱辐射能量的比值随闪光辐射温度的变化而变化；实验测量的可见光谱辐射能量与单位面积辐射能量的理论计算结果的比值决定了辐射源面积的大小。

(3)辐射源面积的演化过程与闪光辐射温度显著不同，当闪光辐射温度达到峰值时(小于10 μs)辐射源面积继续增加，达到峰值(大于20 μs)后缓慢下降。

(4)发光效率随着碰撞角度的增加而降低，碰撞角度为30°时发光效率最高，其最大值为10-5数量级。