不同发光半角的圆形LED阵列辐照特性
张玉宝, 董 礼*, 张国英
(1. 内蒙古科技大学 机械工程学院, 内蒙古 包头 014010;.2. 鄂尔多斯市莱福士光科技有限公司, 内蒙古 鄂尔多斯 017000)
1 引 言
发光二极管(Light mitting,LED)作为第四代照明光源具有节能、环保、体积小、抗震性好、寿命长等优点,被广泛应用于各种照明领域,如显示器中的背光源、路灯以及室内照明等[1-4],在理论上对LED这种新型光源照明特性的研究也越来越受到关注。
由于受制造技术和工艺水平限制,单颗LED的功率极为有限,限制了其在多数照明领域的应用[5]。LED阵列已经广泛地应用在实际的生产生活中,最常用的阵列为圆形LED阵列,其具有中心辐照度值高且辐照均匀性好的特点。在实际的圆形LED阵列的照度特性研究及其应用中,以前学者们主要研究的是LED圆形阵列和方形阵列照度均匀性与结构参数的关系。王加文[6]采用模拟退火算法对LED圆形阵列、矩形阵列进行优化,圆形阵列的最佳半径与LED颗数无关,矩形阵列相邻LED之间的最佳距离与阵列面和目标面之间的距离呈线性关系;赵芝璞[7]推导了LED圆形阵列和方形阵列照度分布函数,采用粒子群(PSO)算法来优化平面随机分布的LED阵列结构,使其在目标光照平面上光照分布均匀;阙笑语[8]利用模拟退火的算法,使LED阵列照明曲面目标面(圆柱形曲面、抛物形曲面和正弦型曲面)产生均匀的照度分布。
目前影响圆形LED阵列辐照特性的因素还存在两个问题有待进一步深入研究:一是对光斑半径的大小没有做准确的定义,导致得出的圆形LED阵列辐照特性的结果不是特别可靠;二是没有考虑到单颗LED发光半角对辐照特性的影响,其中的辐照特性包括中心照度、光斑半径、发散角和辐照均匀性等参数。市面上常见的LED不全是标准的朗伯光源,而是近朗伯光源分布,所以对不同发光半角的LED研究很有价值,本文将对以上两个方面展开进一步的分析和探究。
2 理论与模型的建立
理想情况下,单颗LED光源是近似朗伯光源,即LED的光强分布是观察角的余弦函数[9]。实际上由于封装和芯片形状的原因,其照度分布为观察角余弦多次方的函数,照度的实际分布为:
E(r,θ)=E0(r)cosmθ,
(1)
其中θ是发光角度,E0是轴向与LED距离为r处的照度值。m值取决于芯片相对于LED封装透镜曲面中心的距离。如果芯片位置与曲面中心对应一致,则m≈1,光源近似为一个完美的朗伯光源。m的取值可以通过发光半角θ1/2(发光强度值为轴向强度值一半时发光方向与光轴之间的夹角)来确定[10]:
(2)
当发光半角不同时,对应的m值如表1所示。
表1不同发光半角对应的m值
Tab.1 Correspondingmvalues for different luminous half angles

θ12/(°) m7.580.71520304.8245260175 0.52
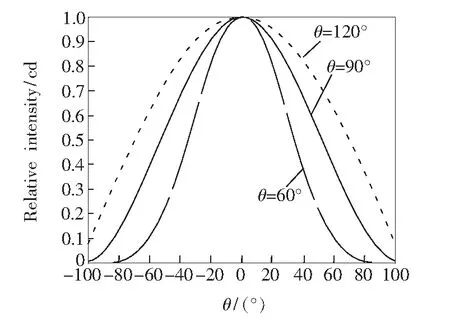
图1 相对矩形光强分布图
图1是发光角度为60°、90°、120°对应的矩形光强分布。
而实际中常采用极坐标的配光曲线的形式,图2依次为利用Tracepro模拟的7.5°~75°的近朗伯型的LED配光曲线。
当LED照射到与其光轴方向垂直的平面时,在该平面上光照度分布与LED空间光强分布由公式(3)确定,是非理想朗伯体光源[11-13]:
(3)
将公式(3)用直角坐标系表示,则xy平面内的LED光源照射到目标平面上任意一点P(x,y,z)的辐照度可表示为:
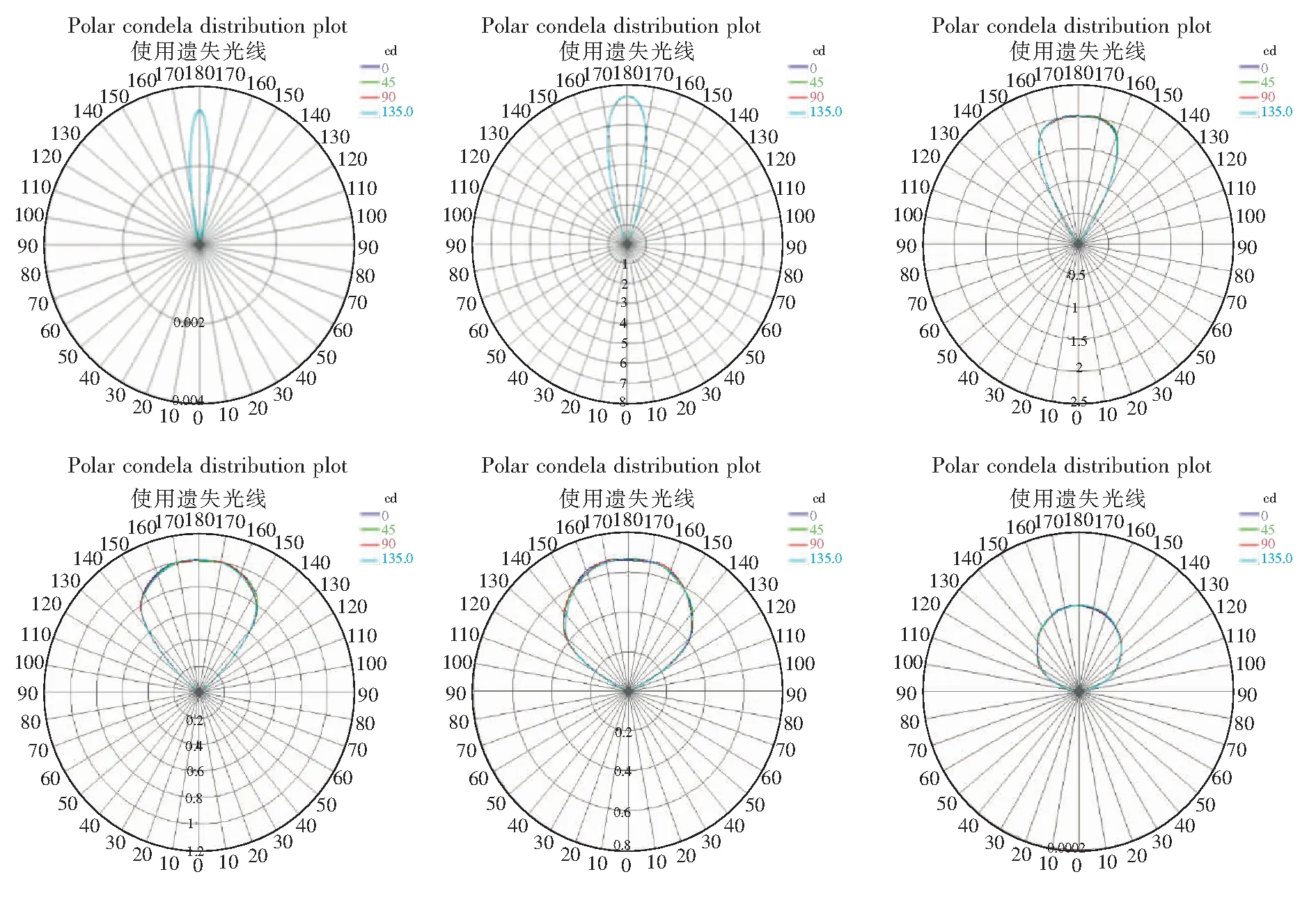
图2 7.5°~75°极坐标下的配光曲线
(4)
其中,(x0,y0)为LED分布在xy平面上的坐标,z为发光面距离接收面的距离,对于圆形LED阵列,排布方式如图3所示。假设圆形阵列上有N颗LED(N≥3),由于LED是非相干光源[14],目标面上的照度为单个LED照度的线性叠加,即P点的照度是圆形阵列上多颗LED共同照射叠加的结果,由公式(4)得到P(x,y,z)点的照度为:
E(x,y,z)=
(5)
依据国际照明学会(IES)规定,截取法向光强10%作为被照面有效光斑区域,所形成的夹角为发散角。故本文选取0.1E0作为被照面光斑边界,即
E≥0.1E0,
(6)
通过公式(6)可得光斑半径R,rN为圆形阵列最大圆周半径,圆形LED阵列的发散角α可表示为:
(7)

图3 LED圆形阵列模型
3 圆形阵列发光特性与单颗LED发光半角的关系
初始条件的设定:本文中采用圆形阵列的LED个数为12个,均匀分布在rN=0.15 m的圆周上,接收面设定为半径为1.784 m、面积为10 m2的圆盘。LED发光面距离接收面距离z=1 m,LED光源定义为面光源,单颗LED的半径为0.015 m,厚度为0.01 m,光源的发光半径也为0.015 m,光通量定义为0.1 lm,具体的发光模型如图4所示。
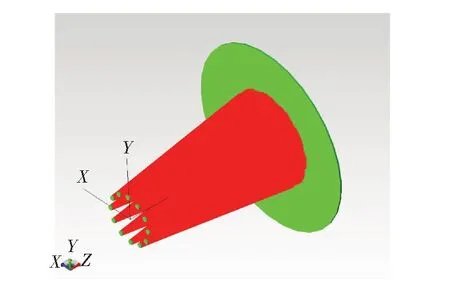
图4 LED阵列发光模型
在目标距离z=1 m的情况下,利用光学仿真软件Tracepro修改单颗LED的发光半角为7.5°、15°、30°、45°、60°、75°,得出对应情况下的光斑半径R、发散角α及中心照度E0如表2所示。
表2圆形阵列中心照度E0、光斑半径R及发散角α
Tab.2 Central illuminanceE0, spot radiusRand divergence angleαof circular array
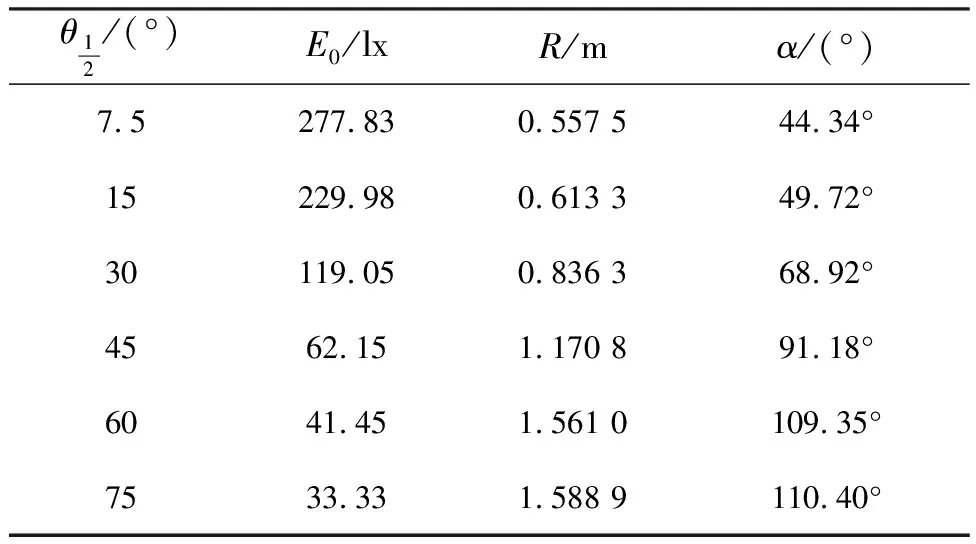
θ12 /(°)E0/lxR/mα/(°)7.5277.830.557 544.34°15229.980.613 349.72°30119.050.836 368.92°4562.151.170 891.18°6041.451.561 0109.35°7533.331.588 9110.40°

(8)
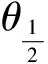
-0.02182θ+0.6871,
(9)
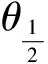
0.484θ+46.31,
(10)
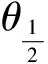

图5 中心照度E0随发光半角的变化曲线
Fig.5 Change curve of center illuminanceE0with luminescent half angle
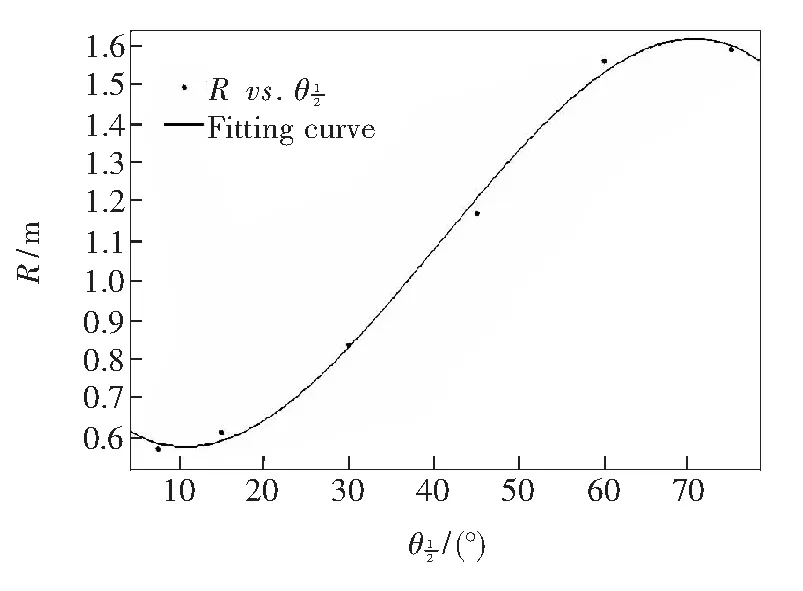
图6 光斑半径R随的变化曲线Fig.6 Variation curve of the radius R of the spot of light
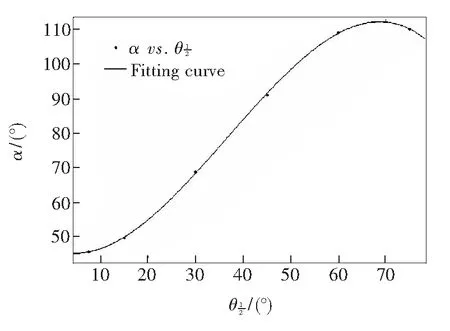
图7 发散角α随的变化曲线Fig.7 Curve of divergence angle α
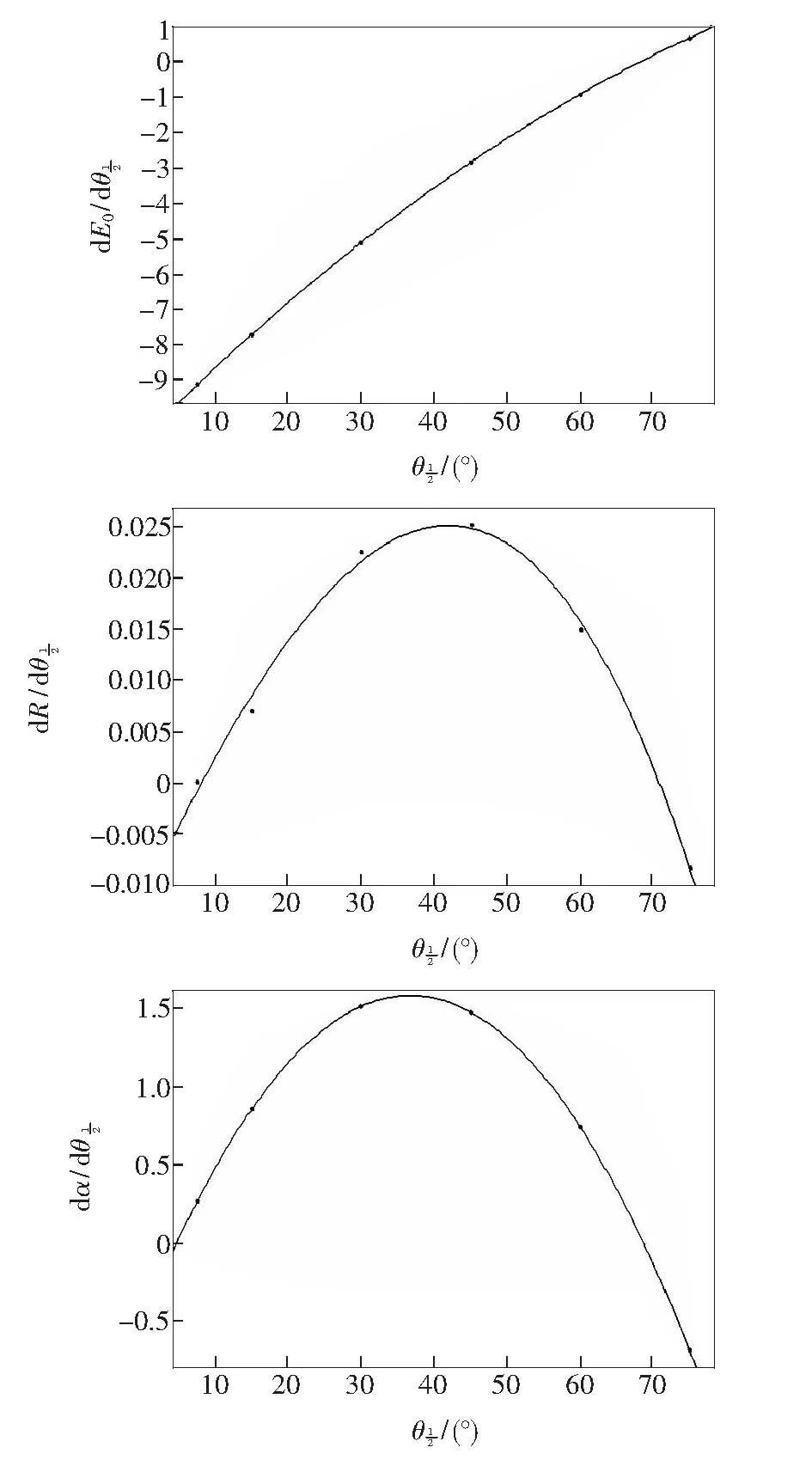
图8 圆形阵列曲线变化率
4 圆形阵列辐照均匀性的研究
实际照明中不仅仅对LED的中心照度、光斑半径和发散角有要求,对辐照均匀性也有要求。以往对辐照均匀性的研究常利用五点法[15],但采用五点法测量照度的均匀度存在许多缺陷,例如取样点太少、没有定义有效光斑半径等。而本文对有效光斑半径给出了明确的定义,在有效光斑半径下去研究辐照均匀性更加合理可行,定义辐照均匀度u为[6]:
(11)

表310m2时不同发光半角对应的辐照均匀性
Tab.3 Irradiance uniformity under different illuminant half angles under 10 m2

θ12/(°)u7.50.393 4150.397 8300.427 2450.437 5600.352 6750.345 5
从表3中可以看出,随着单颗LED发光半角的增大,辐照均匀性u先增大后减小,在45°时取得最大值,但是辐照均匀性还是不理想,可能是由于接收面的面积太大导致的。为了进一步探究发光半角与接收面的关系,依次修改接收面的大小为8,6,4,2,1 m2,发光半角与辐照均匀性的关系如表4所示。
为了能更清晰地看出不同接收面面积下发光半角与辐照均匀性的关系,利用MATLAB画出变化的图像如图9所示。

表4不同接收面面积下发光半角与辐照均匀性的关系
Tab.4 Relationship between radiation half angle and irradiation uniformity under different receiving area

面积/m2θ12/(°) 864217.50.396 60.399 20.408 10.441 80.499 6150.399 10.401 30.405 10.409 50.410 1300.440 10.451 60.471 30.499 10.611 1450.442 00.446 30.451 60.556 20.652 2600.360 70.388 50.443 80.555 30.649 7750.360 10.388 20.442 90.554 80.646 3

图9 不同接收面面积下的发光半角与辐照均匀性的关系
Fig.9 Relationship between radiation half angle and irradiation uniformity under different receiving area
(12)
其中,r0为最大平坦条件,即是圆形阵列的半径;发光面距离接收面的距离z=1 m;由于发光半角的不同导致m不同。分别求出不同发光半角下的最大平坦条件如表5所示。
修改不同发光半角下的最大平坦条件,得到接收面的大小为10,8,6,4,2,1 m2时,发光半角与辐照均匀性的关系如表6和图10所示。
从表6和图10中可以看出,经过优化后整体的辐照均匀性都在优化前的图形之上,最大的辐照均匀度接近0.8,最小的辐照均匀度也有0.5左右,优化后的辐照均匀性有了较大的提升。且当接收面面积一定时,随着发光半角的增大,辐照均匀性增大。在45°~60°时上升的速度最快,幅度最大;在发光半角为60°时,不同接收面面积下其辐照均匀性都是最好的。在以后的圆形光学阵列设计中,若要使接收面的辐照均匀度较高,可以采用60°发光半角的阵列方式,即单颗LED发光满足标准的朗伯光源分布,这样阵列的辐照均匀度更高。
表5不同发光半角下的最大平坦条件
Tab.5 Maximum flat conditions under different luminescent half angles

θ12/(°)r0/m7.50.155 5150.301 530 0.541 5450.707 1600.816 5750.890 9
表6优化后不同发光半角的不同接收面面积下发光半角与辐照均匀性的关系
Tab.6 Relationship between luminous half angle and irradiation uniformity under different receiver half area with different luminous half angles after optimization

面积/m2θ12/(°) 10864217.50.453 00.486 70.534 90.567 10.578 00.577 3150.432 00.446 00.468 10.506 40.563 40.610 8300.475 90.484 80.493 60.501 80.603 00.632 8450.440 70.448 80.491 10.558 60.643 50.692 8600.520 40.573 40.640 70.718 80.774 90.779 475°0.597 40.631 90.691 80.750 20.777 00.778 2
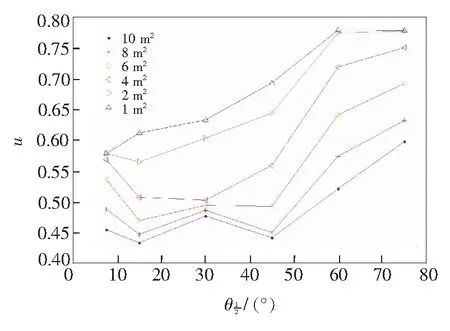
图10 优化后不同接收面面积下的发光半角与辐照均匀性的关系
Fig.10 Relationship between radiation half angle and irradiation uniformity under different receiver surface area after optimization
5 结 论
本文利用Tracepro软件对不同发光半角的圆形LED阵列进行模拟仿真,对得出来的数据结果使用MATLAB软件进行函数数值的拟合分析。探究了单颗LED发光半角与圆形LED阵列发光特性的关系和对辐照均匀性的影响,得出的主要结论如下:
(1)随着单颗LED发光半角的增大,圆形阵列的中心照度值逐渐降低,且降低的速率近似线性增长;光斑半径和发散角都逐渐增大,变化率先增大后减小。在发光半角为40°左右时,光斑半径和发散角增长速率较快,但中心照度值偏低。
(2)在探究圆形阵列辐照均匀性的时候摒弃了传统的五点法,在有效光斑半径下去研究辐照均匀性更加合理可行。辐照均匀度随着发光半角的增大而增大,而后保持稳定;接收面的面积越小辐照均匀度越高。经过优化后,整体的辐照均匀度有了很大的提升,当接收面面积一定时,随着单颗LED发光半角的增大,辐照均匀度增大,发光半角为60°的圆形阵列辐照均匀性最好。
实际工程实践中需要根据实际需要,充分考虑到中心照度值、光斑半径、发散角、辐照均匀性等因素来选择合适的阵列形式。利用Tracepro模拟仿真时没有附加任何的光学系统,因而不存在能量损失,这样再利用MATLAB去拟合不同发光半角对辐照特性的关系会更加可靠准确,为实现圆形LED阵列照明设计提供了理论依据。

