偏置磁场对Fe-Ga合金磁致伸缩导波传感器性能的影响∗

翁 玲，郝永超，李薇娜，孙 英，黄文美，王博文

(1.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学)天津300130；2.河北省电磁场与电器可靠性重点实验室(河北工业大学)天津300130)

磁致伸缩导波检测技术作为无损检测技术的热点研究方向，具有非接触检测、提离距离大、传播距离远和检测效率高的特点，只需单点激励即可实现长距离检测[1]，被广泛应用于桥梁缆索、工业管道等棒状、管状以及束状构件的在役检测和长期监测[2]。传统的磁致伸缩导波传感器[3－4]利用铁磁性待测试件自身的磁致伸缩特性来达到检测目的，但这些材料的本身的应变小，导致传感器的振动位移小，影响了传感器的换能效率。而Fe-Ga合金(Galfenol)是继超磁致伸缩材料Terfenol-D之后的另一种新型磁致伸缩材料[5]，具有应变大、磁滞小、响应时间短等优点，是新型致动器、传感器、振动发电机等各种超磁致伸缩换能器的优选材料[6]。

偏置磁场是磁致伸缩导波检测的关键影响因素之一，对于选择导波模态、提高磁声换能效率、消除倍频效应以及改善信噪比具有极其重要的作用[7]。文献[8]分析了永磁体厚度变化与EMAT换能器灵敏度之间的关系，确定了永磁体的最佳厚度并且研究永磁体和线圈的间距变化对磁感应强度之间的影响。文献[9]通过采用有限元分析建模研究了一种新的提高磁场强度的永磁体放置结构，提高了超声回波信号的幅值。文献[10]在对构件与空气分界面处磁场分布理论的基础上，结合偏置磁场的作用机理，提出了永磁式磁致伸缩纵向导波传感器的换能效率快速评估方法。文献[11]用实验证明，使用磁致伸缩传感器进行导波检测中，偏置磁场对不同材料试件的影响趋势是一致的，但是在不同的材料和不同激励条件下，偏置磁场的最佳区域略有不同。文献[12]分析了偏置磁场均匀性对传感器输出特性的影响，推导了偏置磁场与检测效率的关系，但是不考虑静态磁场不均匀性将会导致一定的计算误差。文献[13]以接收区域静态磁场不均匀为基础，研究了偏置磁场的提离效应，但是并未考虑偏置磁场对接收电压的影响。

本研究提出以Fe-Ga合金为核心部件构建的导波传感器模型可应用于无损检测，其原理为磁致伸缩效应及其逆效应。铁磁体在外磁场激励下产生应变从而激发应力波，当存在缺陷时，其声阻发生变化从而引起接收端电压变化，通过测量电压信号即可检测出铁磁体构件中是否存在腐蚀、裂纹、破损等缺陷。本文基于Fe-Ga合金材料本身的非线性本构关系，计算得到磁致伸缩导波传感器换能效率的最大值点对应的施加磁场强度值。通过实验测量了Fe-Ga合金材料的静态特性，初步找到了Fe-Ga合金材料的最佳工作磁场强度范围。将Fe-Ga合金材料的非线性特性耦合到传感器模型中，利用comsol软件对磁致伸缩导波传感器进行建模仿真，研究了非均匀偏置磁场的提离效应，以及Fe-Ga合金材料表面磁场分布、应变分布。分析了非均匀偏置磁场对传感器接收电压的影响，最终确定了能使传感器换能效率较大且输出应变较大的最佳静态偏置磁场的值。

1 偏置磁场的选择

1.1 Fe-Ga合金材料的非线性本构关系

磁性材料的磁致伸缩特性是磁致伸缩传感器能够正常工作的关键因素。在导波的激励、传播和接收过程中存在着复杂的磁机耦合关系。在之前的研究中，由于磁致伸缩特性的复杂性(非线性、磁滞效应)，将材料的非线性磁致伸缩关系假定为线性关系[14]，没有体现出材料真实的非线性磁致伸缩关系，从而本文采用文献[15]提出的非线性磁机本构关系。

Fe-Ga材料的应变ε：

磁场强度H：

式中：M为Fe-Ga合金材料的磁化强度，Ms为饱和磁化强度，λs为饱和磁致伸缩应变系数，χm为初始磁化系数，σ为预应力，σs为饱和预应力，μ0为真空磁导率，H为Fe-Ga合金材料的外部磁场。

磁致伸缩传感器Fe-Ga合金材料的外部磁场分别是由永磁体提供的静态磁场Hd和交变线圈组提供的动态磁场Hac两部分构成。由于静态磁场远远大于动态磁场，在计算中常常忽略动态磁场，用静态磁场Hd来近似代替Fe-Ga合金材料的外部磁场H。在下述推导中用静态磁场Hd代替外部磁场H。

Fe-Ga材料表面预应力为零时，由式(1)和式(2)可知[16]：

联立式(3)和(4)可得

对式(5)求偏导可以得到压磁系数，

利用MATLAB对式(6)进行求解，可得压磁系数与磁场强度之间的关系如图1所示。其中χm＝200，λs＝0.000 2，Ms＝1.5×106 A/m。 随着磁场强度的增大，压磁系数的值先增大后减小最后趋于稳定，当磁场强度为4.8 kA/m时，压磁系数达到了最大值1.56×10－8m/A。压磁系数表征了磁致伸缩的换能效率，当Fe-Ga合金材料的压磁系数达到最大值时，换能效率达到了最大，此时更多的磁能转化为了机械能。因此在选择偏置磁场时，为保证传感器的能量转换效率，应尽量选择压磁系数最大值对应的磁场强度附近。

图1 磁场强度和压磁系数的关系

1.2 Fe-Ga合金材料静态特性测量

测量Fe-Ga合金材料的静态特性有助于确定磁致伸缩导波传感器的输入量和为永磁体的选择提供依据。本文搭建了Fe-Ga合金磁特性测量系统如图2所示。本系统由四个模块组成，施加磁场模块、信号测量模块、信号采集模块、数据处理模块组成。对Fe-Ga合金材料进行静态磁特性测量时，首先将压片机输出的压力置为0，给激励线圈施加1 A～5 A的直流电，此时Fe-Ga合金材料处于激励线圈提供的有效磁场中，Fe-Ga合金材料周围的磁场值可以通过材料表面的霍尔元件测量得到，Fe-Ga合金材料的应变值可以通过粘贴在材料表面的应变片测量得到。数据处理模块将采集到的信号进行处理，得到Fe-Ga合金材料的静态磁致伸缩曲线。

图2 实验平台

利用MATLAB对式(5)进行求解，可得Fe-Ga合金材料的磁致伸缩曲线。Fe-Ga合金材料的静态磁致伸缩曲线实验结果与仿真结果的对比如图3所示。随着施加磁场强度的增大，Fe-Ga合金材料的应变值先增大后趋于稳定。当Fe-Ga合金材料的饱和磁致伸缩量为200×10－6时，所对应的磁场强度为20 kA/m。结合最佳偏置磁场选择的理论分析和实验结果的分析，并考虑到Fe-Ga合金材料表面磁场分布不均，为使材料的应变达到最大且保证传感器的换能效率，最佳偏置磁场应该使Fe-Ga合金材料表面磁场强度值达到5 kA/m～20 kA/m，应变值在100×10－6～200×10－6左右。

图3 实验结果与仿真结果对比

2 导波传感器的建模

2.1 传感器的工作原理

本文采用文献[17]中的Fe-Ga合金磁致伸缩导波传感的结构参数。传感器结构如图4所示，主要由圆柱状铷铁硼永磁体、线圈组、Fe-Ga合金材料和待测铝板组成。将线圈置于Fe-Ga合金材料周向的上方，永磁体置于Fe-Ga合金材料的正上方。永磁体提供恒定的偏置磁场，偏置磁场用于消除倍频作用，还可以增加Fe-Ga合金材料的最大磁致伸缩变形[14]，线圈提供高频交变磁场。外侧矩形为静态磁场方向，内侧矩形为动态磁场方向。永磁体在Fe-Ga合金材料产生沿径向辐射的静磁场分量，线圈组在Fe-Ga合金材料表面也产生沿径向分布的动磁场分量，即永磁体和线圈在Fe-Ga合金材料表面的磁场分布方向一致。导波的产生过程：Fe-Ga合金材料基于磁致伸缩效应(焦耳效应)在静磁场与交流磁场的共同作用下产生应变，应变以应力波的形式耦合到铝板中进行传播。导波的接收过程：当应力波传到接收传感器时，Fe-Ga合金材料基于磁致伸缩逆效应(维拉里效应)周围的磁感应强度发生变化，线圈根据法拉第电磁感应定律感应出电压。

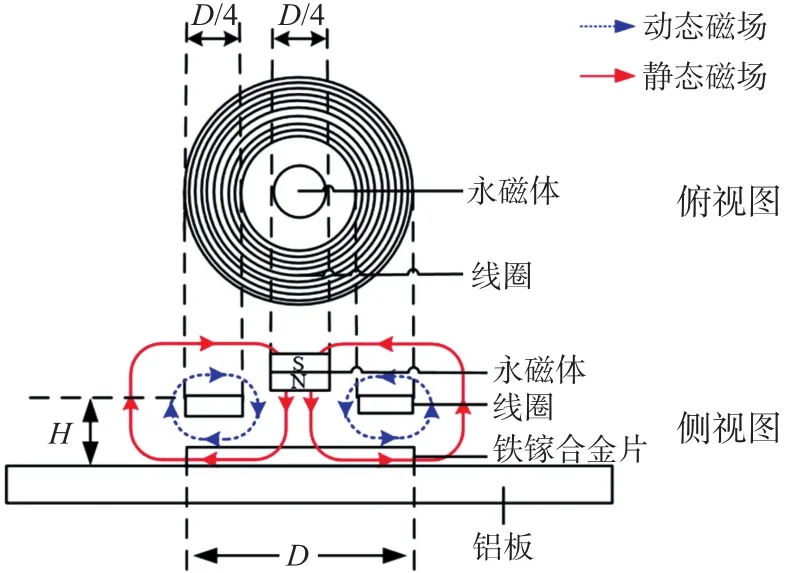
图4 传感器的结构

2.2 传感器仿真模型的建立

磁致伸缩导波传感器仿真模型如图5所示。传感器包含激励端和接收端，且两端采用相同的结构。模型包含三个计算区域，分别是磁场计算区域、力学计算区域和声学计算区域，其中激励端磁场和接收端磁场分开计算。本文利用comsol软件的AC/DC模块、固体力学模块和声学模块对以上区域进行求解。首先计算激励端中的磁场分布，包含永磁体、线圈、Fe-Ga合金材料、铝板及空气域的静态磁场和动态磁场。接下来分析Fe-Ga合金材料的应变和应力分布。然后通过将力学场与声学场进行耦合从而求解得到导波在铝板中的传播。最后通过计算接收端中的Fe-Ga合金材料的应力和应变，根据磁致伸缩逆效应和法拉第电磁感应定律，求解得到线圈中的感应电动势。

图5 仿真模型

铝板的尺寸为200 mm×200 mm×1 mm，电导率为3.774×107S/m，密度为2 700 kg/m3，激励端和接收端相距100 mm，杨氏模量为70 GPa，泊松比为0.33，相对磁导率为1。Fe-Ga材料尺寸为 ϕ25.4 mm×0.5 mm，电导率为 7×106S/m，密度为 7 870 kg/m3，杨氏模量为60 GPa，泊松比为 0.45，饱和磁化强度为 1.5×106A/m，饱和磁致伸缩为 2×10－4，初始磁化率为200。激励端传感器和接收端传感器相距为100 mm。激励端传感器和接收端传感器中线圈组的匝数均为112匝，电导率为6×107S/m。激励端传感器加载频率为100 kHz，最大幅值为1 A的窄频信号如图6所示。

图6 激励信号

3 偏置磁场对传感器性能的影响

3.1 提离距离对接收电压的影响

提离距离即永磁体的下表面到Fe-Ga合金材料表面的距离。提离距离的大小直接影响着Fe-Ga合金材料表面的磁场分布，从而影响到接收端电压的幅值。提离距离与接收端的电压峰值之间的关系如图7所示，当永磁体的剩余磁通密度为0.5 T时，随着提离距离的增大，接收端的电压峰值逐渐减小最后趋于稳定。当初始提离距离为1.54 mm时，电压峰值达到了最大值为0.11 V；当提离距离大于7 mm时，提离距离对接收电压的影响逐渐减小，电压值趋于稳定并保持为0.002 8 V。由图7可知，提离距离越小，接收端电压的幅值越大。考虑实际工程中，线圈和永磁体需要固定在Fe-Ga合金材料表面，但永磁体不可能无限接近于Fe-Ga合金材料表面，即永磁体和Fe-Ga合金材料表面需留有一定空隙，所以最终选择提离距离为2.5 mm。

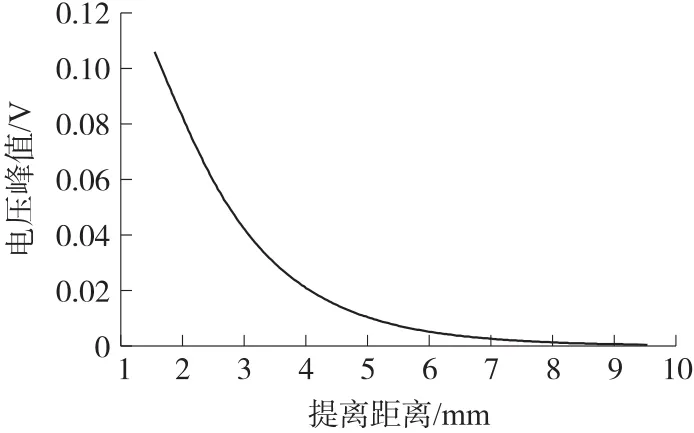
图7 提离距离对接收电压的影响

图8 Fe-Ga材料表面磁场和应变

3.2 偏置磁场对应变和接收电压的影响

永磁体提供的静态偏置磁场在导波的激励、传播和接收过程起着非常关键的作用。为研究静态偏置磁场大小对传感器的影响，以下讨论中保持永磁体提离距离不变(H＝2.5 mm)。在导波激励过程中，永磁体在Fe-Ga合金材料表面引起的磁场分布和应变如图8所示，横坐标为Fe-Ga合金材料沿直径方向的坐标参量，纵坐标分别为Fe-Ga合金材料的磁场强度和应变。随着永磁体提供的剩余磁通密度的增加，Fe-Ga合金材料的磁场强度和应变值逐渐增大。在永磁体提供的剩磁为1.7 T时，Fe-Ga合金材料表面最大磁场强度达到了21 kA/m，应变值达到了110×10－6。。但在实际应用中，永磁体主要由铁氧体、铝镍钴合金或者是稀土磁铁(钕铁硼及钐钴)构成，而稀土材料构成的永磁体产生的磁场最大，但一般也不能超过1.4T，能够提供最大稳定值一般在1.0 T左右，所以在选择永磁体时，本文选择剩余磁通密度为1.0T。Fe-Ga合金材料表面最大磁场强度达到了8 kA/m，应变值达到了40×10－6。

在导波接收过程，静态偏置磁场大小对接收端的电压幅值和应变有着直接的影响。本文选取接收端中心点处的应变作为观测点。接收端的应变和电压如图9所示。由图9(a)所示，接收端中心点处的应变值随着静态磁场的增大而逐渐增大，在静态磁场为2.1 T 时，应变达到了 9.5×10－6。 由图 9(b)所示，当施加剩余磁通密度为1.0T时，仿真模型计算得到，在时间为10×10－5s～20×10－5s时，传感器接收到的电压波为首次抵达波，此时电压幅值达到0.16 V，其他电压波为首次抵达波的反射波(带侧板两侧的反射波)。由图9(c)所示，随着永磁体剩余磁通密度的增加，接收端的电压幅值也在增加。在剩余磁通密度为1.7 T时，接收端的电压峰值达到了0.33 V。当剩余磁通密度逐渐增加到2.0 T时，电压幅值变化很小，保持在0.34 V左右。当剩余磁通密度大于2.0 T后，接收端的电压幅值有所下降。本文选择剩余磁通密度为1.0 T时，接收端的电压峰值达到了0.15 V。

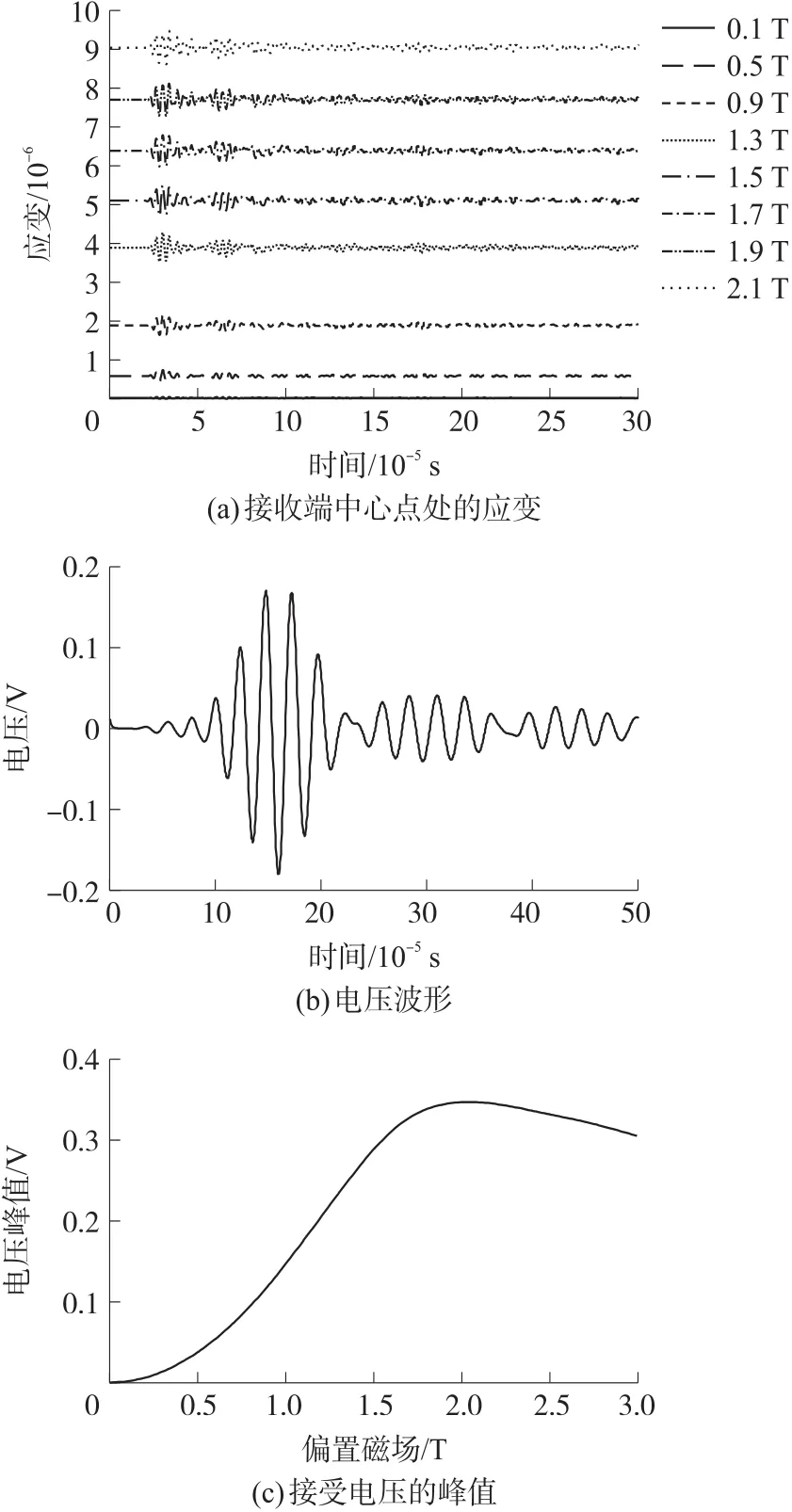
图9 接收端的应变和电压

上述理论分析了偏置磁场对Fe-Ga合金磁致伸缩导波传感器性能的影响，由于磁滞模型的复杂性，本研究暂未考虑材料的磁滞特性对传感器性能的影响。在之后的研究中，会将磁滞模型添加到传感器的仿真模型中，并搭建导波检测实验平台对理论结果进行验证。

4 结论

本文以Fe-Ga合金材料本身的非线性特点为出发点，首先研究了偏置磁场对Fe-Ga合金材料的影响，初步得到了Fe-Ga合金材料处于最佳工作点时，材料表面的磁场强度为5 kA/m～20 kA/m，磁致伸缩应变为100×10－6左右，此时的换能效率最大。将Fe-Ga合金材料的非线性特性耦合到传感器模型中，计算分析了提离距离与接收端电压之间的关系，得出传感器的最佳提离距离为2.5 mm。通过计算分析偏置磁场对激励端的磁场和接收电压的影响，得到了最佳偏置磁场为1.0 T。最后选取非均匀分布的静态偏置磁场大小为1.0 T，提离距离为2.5 mm，仿真计算得到传感器接收端的电压峰值可达到0.15 V。