区域创新效率与经济增长实证研究

张 凡

(华南理工大学 工商管理学院，广东 广州 510640)

一、引言

改革开放近40年来，我国发生了举世公认的巨大变化，但国民经济也从地域和空间上裂变为发达地区与欠发达地区两种明显的类型。在新常态下，甚至出现了发达地区增速高于全国平均水平而欠发达地区增速低于全国平均水平的新情况，不平衡和分化的态势加剧。在我国经济迈向中高端的过程中，创新已超越其他因素，成为决定经济总量提升的最主要因素。在创新与经济增长实证研究方面，已有文献主要关注的是创新投入、创新能力对经济增长影响的实证研究[1-7]，只有极少数学者关注到创新效率与经济增长。Young和Pagán(2003)[8]是为数不多的研究创新效率与经济增长的学者，他们以中小型企业为研究对象，得出效率是影响企业盈利能力的最关键因素的结论。尹向飞和段文斌(2017)[9]建立全要素生产率、技术进步、技术效率改进和各阶段的效率变化等各种效率指标之间的联系，并对中国各省情况进行了探讨，发现科技创新效率对中国经济增长的支撑作用较低。李明和李鹏(2017)[10]研究发现科技创新效率对地区经济的推动作用整体水平不高，且存在明显的地区差异。

区域发展差距有其历史和基础条件的原因，但在全国创新发展的大背景下，主要还是区域创新效率差异的问题。创新效率的提高，有助于优化生产要素的配置，提高全要素生产率，因而能够提高经济产出。创新效率差异已成为我国区域差异的重要表征，成为影响区域竞争力和经济发展的核心因素。那么，我国区域创新效率分布如何，区域之间的联系(空间效应)对创新效率有什么样的影响，创新效率与经济增长到底是什么关系，如何提高区域创新效率，进而如何促进区域协调发展，这些问题成为区域经济发展不可回避的问题。

二、研究设计

(一)创新效率测度方法

在对创新效率进行测度之前需要对生产前沿面进行估计，当前随机前沿法以及数据包络法是主要的估计方法。在估计生产前沿面时，随机前沿法和数据包络法各有优劣。随机前沿法考虑了随机误差的影响，这种处理方法更贴近现实。其次，随机前沿法以计量经济学为基础，既可以考察不同生产要素投入对产出的影响，还可以考察政策环境、市场环境等各种非投入要素对创新效率的影响[11]。本文考察的对象是中国大陆31个省份，而不同省域、不同时期的创新效率可能存在显著差异，有必要考虑随机误差的影响。此外，本文在考察区域创新效率的影响因素时必须以绝对效率水平为基础，而数据包络法得到的是相对效率。因此，本文选取随机前沿法对区域创新效率进行测度。

随机前沿法的基本模型由Aigner等(1977)[12]以及Meeusen和Broeck(1977)[13]同时独立提出，经过Battese和Coelli(1992)[14]等对随机前沿法的基本模型不断的拓展和完善，其灵活性和适用性大为提升。随机前沿法的具体形式如下：

(1)

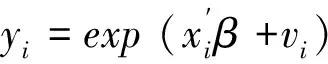
在对区域前沿生产面进行估计时，Cobb-Douglas函数得到了广泛的应用。但是，这种做法具有局限性，即没有对样本个体产出的弹性方面进行考虑。为了使测量结果变得更加准确，本文考虑以超越对数函数作为前沿生产面形式。一般来说，创新的直接投入要素可分为研发人员(RDP)和研发资金(RD)两种，因为创新活动具有一定周期，而上述两个要素都滞后一期。于是，以超越对数函数为基础的随机前沿模型如下：

lnyit=β0+β1lnRDPi(t-1)+β2lnRDi(t-1)+

β3(lnRDPi(t-1))2+β4(lnRDi(t-1))2+

β5lnRDPi(t-1)lnRDi(t-1)+vit+uit

(2)

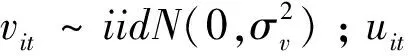
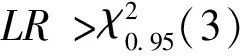
lnyit=β0+β1lnRDPi(t-1)+β2lnRDi(t-1)+

vit+uit

(3)

以新产品产值为产出变量的随机前沿模型最终设定为：

lnyit=β0+θt+β1lnRDPi(t-1)+β2lnRDi(t-1)+

β3(lnRDPi(t-1))2+β4(lnRDi(t-1))2+β5lnRDPi(t-1)

lnRDi(t-1)+vit+uit

(4)

在估计出生产前沿面后，就可以通过下式计算出区域创新效率：

(5)

创新过程可分为两部分：研发和商业化。高校、科研机构和企业是研发的主体，根据市场需求产生新点子，进而研究开发出新技术和设计，在这一过程中会产生论文、专利、产品原型或原始样机等。企业是商业化的主体，企业提供原材料和劳动力等资源，把研发得到的新设计和技术转变为新产品，投入市场销售。为更深入分析创新效率对经济增长的影响，本文将创新效率分解为研发效率和创新经济效率(商业化效率)，在测算研发效率时将发明专利申请量作为衡量产出的指标；在测算商业化效率时，将新产品销售收入作为衡量产出的指标。

(二)创新效率对经济增长影响的空间计量模型

在经济计量学研究中，研究数据往往涉及不同的时间和区域，由于人类的活动是在时空范围进行的，因此经济现象不仅表现出时间方向上的相关，而且在空间方向上也表现出某种程度的相关。在对区域经济问题的研究中，由于区域之间存在着特有的空间特性(通称为空间效应)，使得经典经济计量学假定的条件(Gauss-Markov、解释变量固定等)往往得不到满足，从而经典的经济计量学方法在研究存在空间效应的问题时变得不合适，采用空间计量经济模型能够更准确地揭示区域创新效率与经济增长的关系。

空间计量方法在研究中主要用到两类模型：一是空间误差模型(SEM)，该模型适用于误差项在空间上相关；二是为空间滞后模型(SLM)，适用于当变量间的空间依赖性对模型显得非常关键而导致了空间相关。

创新效率对经济增长影响的空间滞后模型可表示如下：

lnGDPi,t=α0+α1lnRIEi,t+α2lnKi,t+

α3lnLi,t+ρWlnGDPi,t+εi,t

(6)

创新效率对经济增长影响的空间误差模型可表示如下：

lnGDPi,t=α0+α1lnRIEi,t-1+α2lnKi,t+

α3lnLi,t+εi,t

εi,t=γWεi,t+μi,t

(7)

在式(6)、式(7)中，GDP表示经济增长；RIE为区域创新效率，分为区域研发效率和区域商业化效率；K为资本投入，用固定资本存量来反映；L为劳动力，用就业人员来反映。若α0为固定常数，则以上两个模型是固定效应模型；若α0是随机变量，且与其他自变量不相关，则是随机效应模型。当样本随机取自总体时，选择随机效应模型较为恰当，而本文所考察的区域为我国大陆地区的31个省份，样本单位不是随机取自总体，因此采用固定效应模型更加合适。

三、估计结果与分析

本文以中国大陆31个省份(不含港澳台地区)为研究对象，考察期为2009-2016年，数据来源于历年《中国统计年鉴》和《中国科技统计年鉴》。研发资本和固定资本存量通过永续盘存法估算得到。

(一)区域创新效率估计结果与分析

借助Frontier 4.1软件，釆用极大似然法对式(3)、式(4)进行参数估计，具体结果如表1所示。

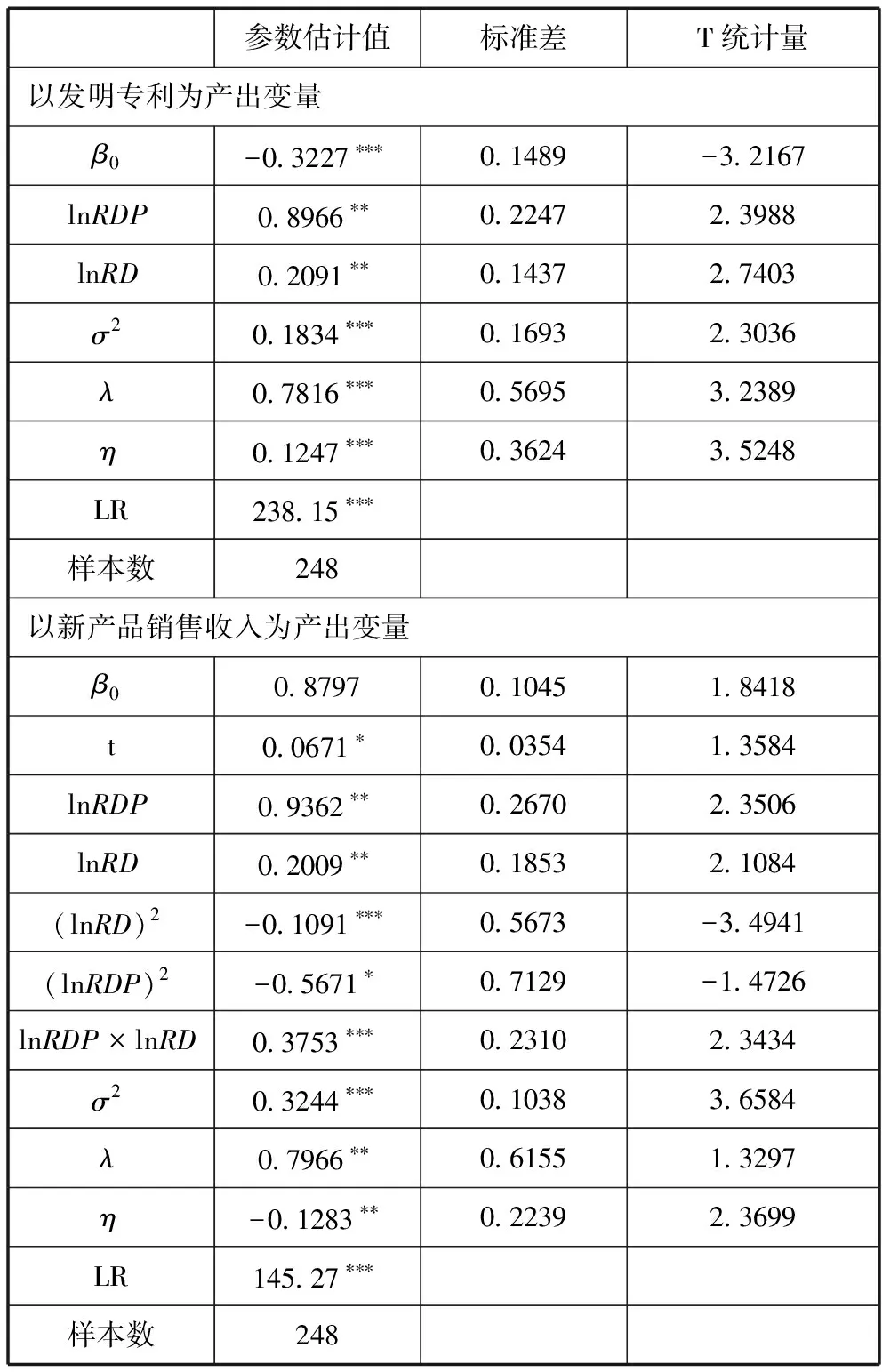
表1 区域创新效率测度模型估计结果

注：***、**、*分别表示在1%、5%和10%水平下显著。

从表1中可以看出，两个模型的LR、σ2和λ都在5%水平下显著，λ的估计值也都大于0.6，说明釆用随机前沿模型是合理的，大部分随机误差都由无效率效应导致。

在表1的基础上，本文进一步计算得到2009-2016年中国区域研发效率(表2)和商业化效率(见表3)。

从表2可以看出，我国大部分区域的研发效率都比较高，其中绝大部分东部区域如北京、天津、上海、江苏、浙江、山东、广东的研发效率都在90%以上。研发效率较低的区域多位于西部如贵州、云南、西藏、甘肃、青海、宁夏、新疆。在东部10个省份中，江苏的研发效率最高，海南的研发效率最低。在中部6个省份中，湖北的研发效率最高，江西的研发效率最低。在西部12个省份中，四川的研发效率最高，西藏的研发效率最低。

从表3可以看出，我国区域商业化效率明显低于研发效率，绝大多数区域在促进科技成果转移转化方面还表现欠佳，制约科技成果转化为现实生产力的各种体制机制障碍还比较多。商业化效率在90%以上的区域有江苏、浙江、广东等民营经济比较发达的省份。和研发效率一样，商业化效率较低的区域多位于西部如西藏、甘肃、青海、宁夏、新疆。在东部10个省份中，广东的商业化效率最高，海南的商业化效率最低。在中部6个省份中，湖南的商业化效率最高，江西的商业化效率最低。在西部12个省份中，重庆的商业化效率最高，西藏的商业化效率最低。

(二)区域创新效率对经济增长影响估计结果与分析

在进行估计前，需要对空间计量模型的适用性进行检验和判断。无论是研发效率空间计量模型还是商业化效率空间计量模型的检验结果均表明LMLAG和R-LMLAG分别通过了1%和5%水平下的显著性检验，而LMERR和R-LMERR均未能通过检验，按照Anselin等(1997)的判断规则，选用空间滞后模型相对比较合适。研发效率对经济增长影响的空间计量经济模型(空间权重矩阵为省份之间质心距离的倒数)的极大似然估计结果见表4。

从调整后R2等和LogL统计量来看，研发效率对经济增长影响的空间SLM模型具有较好的拟合度，表明考虑空间效应以后，用极大似然法估计的模型有效地消除了研发效率和经济增长空间自相关和空间误差，能够较为准确地表达中国区域研发效率对经济增长的促进过程。

变量lnRIE的系数估计值为0.1452，并且通过了5%水平下的显著性检验，说明研发效率的对各省份经济增长有正面的影响：研发效率每增加一个百分点，经济增长率提高0.15个百分点。变量lnK的系数估计值为0.5639，并且通过了1%水平下的显著性检验，说明固定资产投资的增加对各省市经济增长有正面的影响：固定资产投资每增加一个百分点，经济增长率提高0.56个百分点。变量lnL的系数估计值为0.3157，并且通过了5%水平下的显著性检验，说明劳动力投入的增加对各省份经济增长也有正面的影响：劳动力投入每增加一个百分点，经济增长速度提高0.32个百分点。经济增长的固定资产投入弹性比劳动力投入弹性大，表明我国经济增长仍以资本驱动为主。

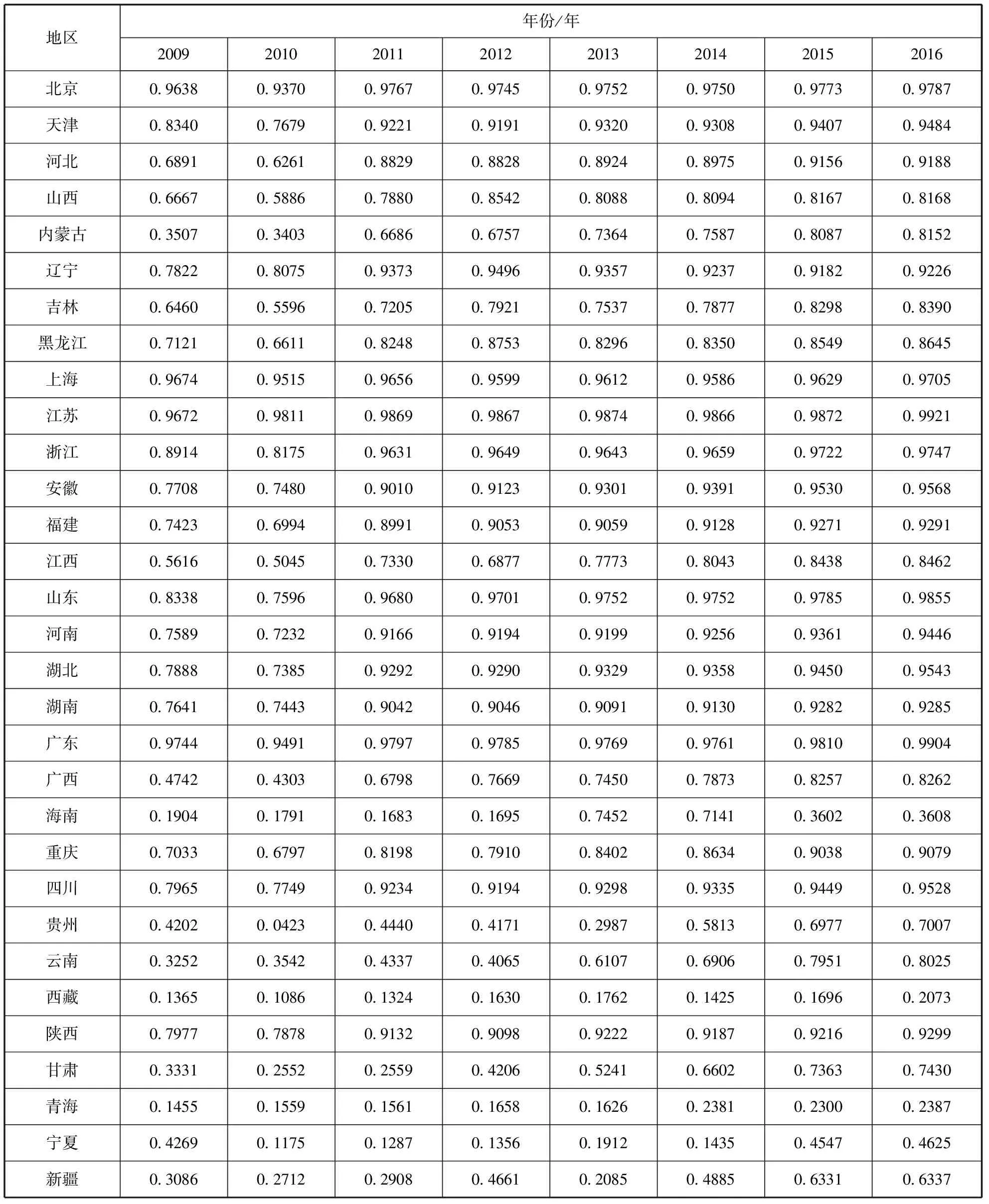
表2 2009-2016年各区域研发效率

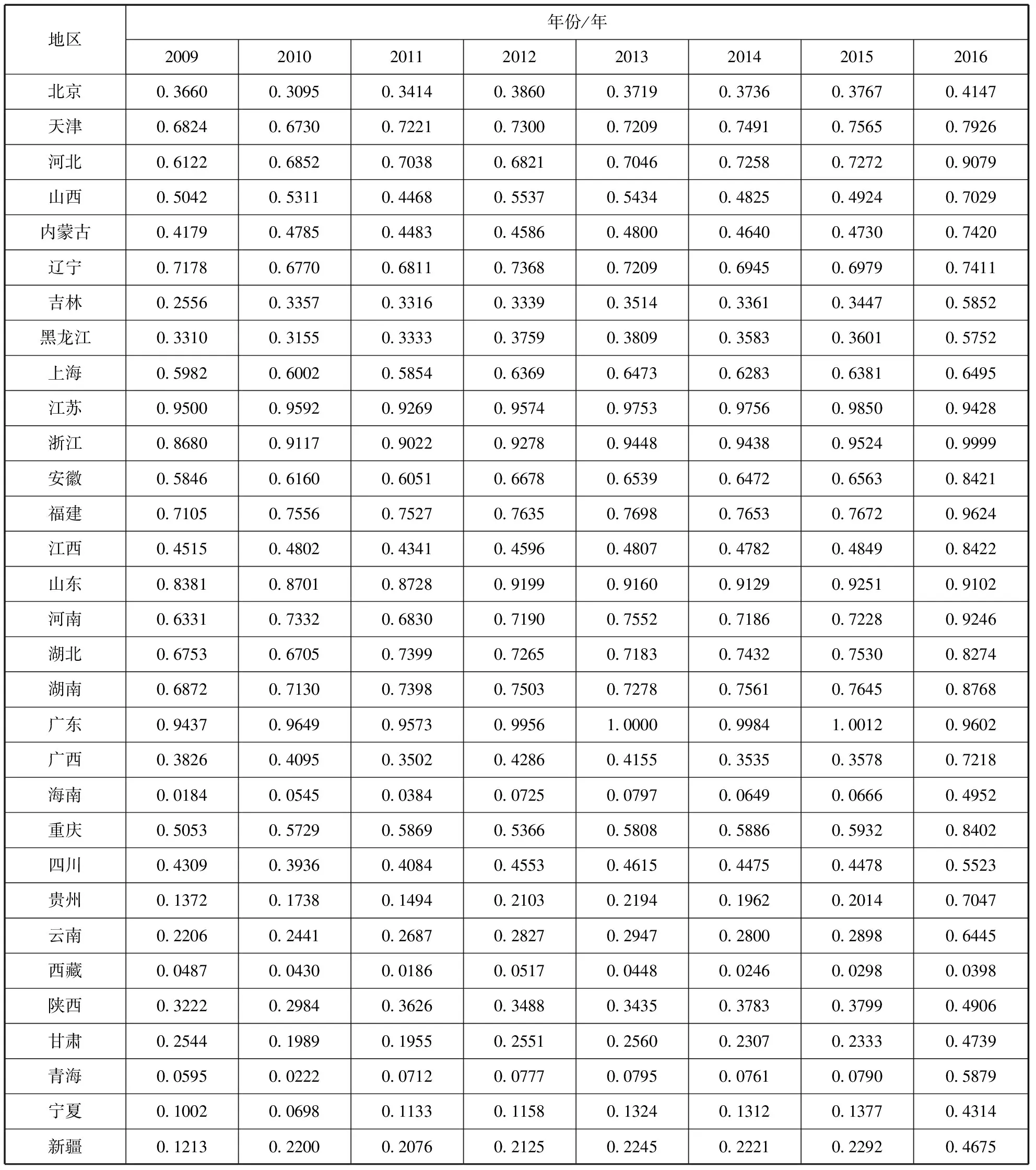
表3 2009-2016年各区域商业化效率

空间滞后因变量WlnGDP的系数估计值为0.0798，并且通过了1%水平下的显著性检验，说明省际间的经济增长存在显著的正的空间自相关，也就是说经济增长在省际间存在溢出效应，一个区域的快速经济增长对邻近区域的产出能产生正的溢出，我国大部分经济发展较快的区域对周边地区能发挥明显的带动作用。这表明，我国以增长极理论为基础的非均衡型区域经济发展战略取得了成功。但是，也应该看到，尽管我国经济增长在省际间存在溢出效应，但与研发效率对经济增长的影响相比，这种溢出效应还不大，区域增长极的辐射带动潜力还有待增强。

商业化效率对经济增长影响的空间计量经济模型的极大似然估计结果见表5。

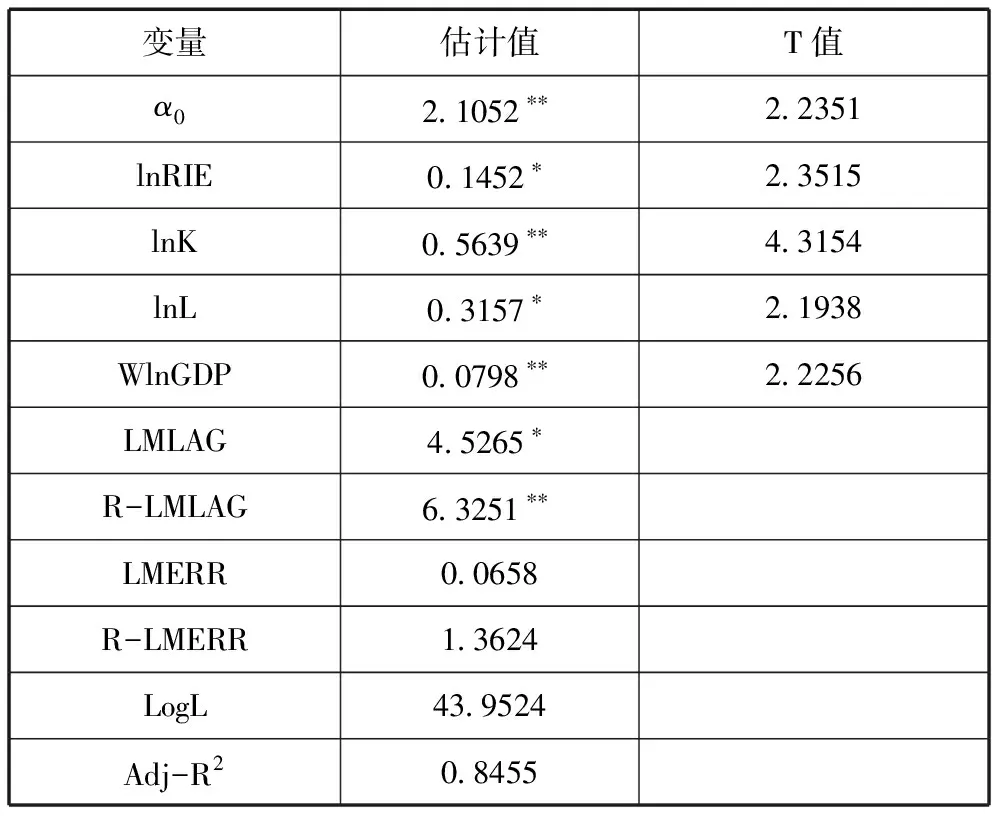
表4 研发效率对经济增长影响的

注：**和*分别表示在1%和5%水平下显著。

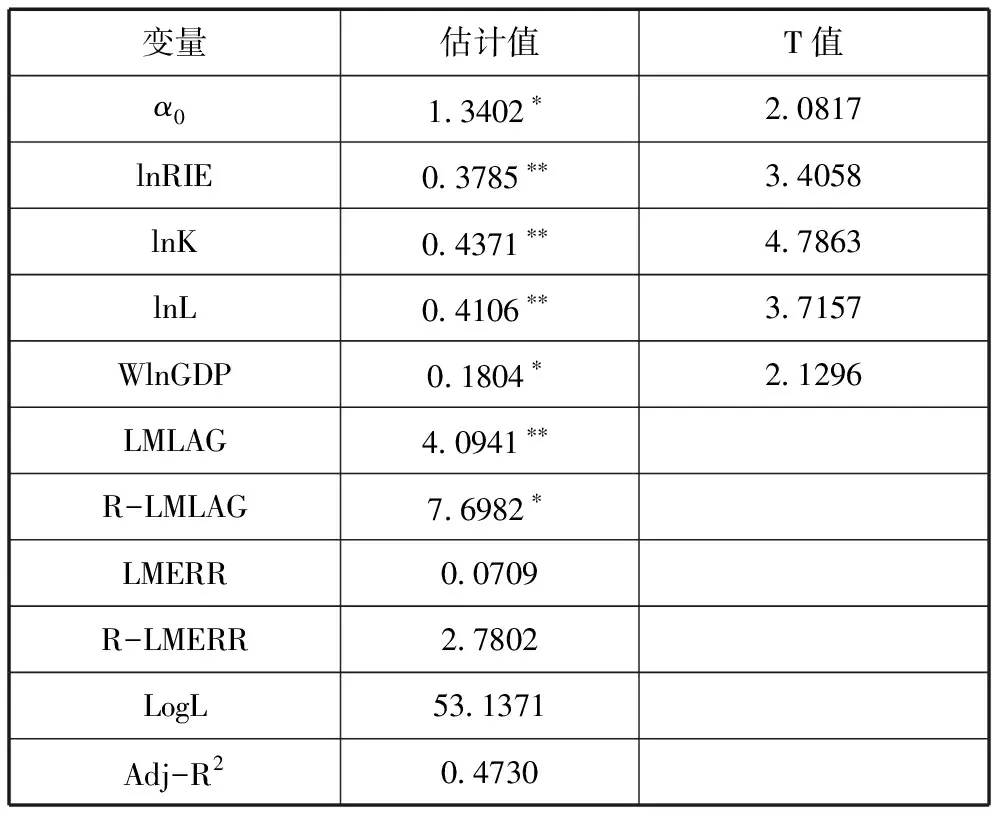
表5 商业化效率对经济增长影响的

注：**和*分别表示在1%和5%水平下显著。

从调整后R2等和LogL统计量来看，模型能够较为准确地表达中国区域商业化效率对经济增长的促进过程。

变量lnRIE的系数估计值为0.3785，并且通过了1%水平下的显著性检验，说明研发效率的对各省份经济增长有正面的影响：商业化效率每提升一个百分点，经济增长率提高0.38个百分点，比研发效率对经济增长的影响大。商业化效率对经济增长影响的空间计量经济模型中，尽管经济增长的劳动力投入弹性比固定资产投入弹性小，但两者已经接近。

与研发效率对经济增长影响的空间计量经济模型一样，空间滞后因变量WlnGDP的系数估计值为正，并且通过了5%水平下的显著性检验，说明我国经济增长在省际间存在溢出效应，但与商业化效率对经济增长的影响相比仍偏弱。

四、研究结论与政策建议

本文对区域创新效率(包括研发效率和商业化效率)进行了测度，并建立空间计量模型，对创新效率对经济增长的影响进行了检验，研究结果表明：(1)无论是从研发效率，还是从商业化效率来看，东部地区都处于相对领先地位，中部地区紧随其后，西部地区的创新效率最低。我国区域商业化效率明显低于研发效率，除少数民营经济较为发达的地区外，我国绝大多数区域在促进科技成果转移转化方面还表现欠佳，制约科技成果转化为现实生产力的各种体制机制障碍还比较多。(2)创新效率对区域经济增长有正面的影响，但不及资本和劳动力对区域经济增长的影响大，创新尚未成为推动我国区域经济增长的主要动力。(3)尽管我国经济增长在省际间存在溢出效应，但与创新效率、资本、人力投入对经济增长的影响相比，这种溢出效应还不大，区域增长极的辐射带动潜力还有待增强。

根据上述研究结论，本文提出如下政策建议。

一是建立科技成果转化协调机制。科技成果转化涉及研究、开发、商品化转化、产业化等环节，以及资金、技术、人才、信息等多方面要素，各级政府要设立跨部门的科技成果转化政策协调服务机构，协调解决科技成果转化中的政策落实问题，提高商业化效率。

二是加强创新能力建设。各地区要加大创新投入，加强重点实验室、技术创新中心、工程研究中心、公共技术服务平台、中试基地等科技创新基地和平台建设，加大人才的吸引和培育力度，提高创新效率，使科技创新成为引领区域发展的第一动力。

三是促进区域协同创新。要协调建立资源共享机制，建立资源市场平台，形成良好的市场环境，让市场在资源配置中起决定性作用，打破地区行政保护和垄断，促进资源多向流动。各地区位条件、资源禀赋、发展基础都不一样，需要结合自身优势寻找科技创新和产业升级路径，避免产业发展雷同，造成资源浪费。