一种钢质围网渔船波浪运动响应分析

马瑶珠，赵 陈，姜 华，徐行天

(1.浙江国际海运职业技术学院，浙江舟山 316021；2.太平洋海洋工程(舟山)有限公司，浙江舟山 316057；3.浙江海洋大学船舶与机电工程学院，浙江舟山 316022)

上世纪80 年代以来，围网作业方式迅速发展，渔船采用围网方式进行捕捞的比例逐步提高。一般围网渔船型线简单，船长较小，吃水较浅，但是需要在风浪中连续航行、作业，要求有较好的稳定性、耐波性和适航性。海浪作为海水运动的主要形式之一，是影响渔船安全航行的主要海洋环境因素。由于波浪的入射角不同，渔船会出现升降、摇摆运动和中拱、中垂等危险情况而造成碰撞、搁浅、触礁等渔船事故。因此，开展渔船在波浪中的运动响应预报分析显得尤为重要。

目前，国内外学者开展了大量船舶耐波性CFD 的研究工作，取得了若干研究成果：吴乘胜等[1]、WEYMOUTH，et al[2]对规则波中的Wigley 船模进行了顶浪航行下的纵摇和垂荡耦合运动数值模拟；WILSON，et al[3]进行了ITTC S175 船模规则波中顶浪大幅运动的数值模拟；DIEN，et al[4]研究了不同船型对小型围网渔船横摇运动的影响。虽然国内外众多专家和学者对船模进行了许多理论和实验研究，但实船与经典船模有所差异，对实船的运动响应模拟研究较少，针对围网渔船运动响应的研究更是稀缺。

本文以1 艘8.3 m 型宽远海航区钢质围网渔船为研究对象，通过1:1 船体建模，运用CFD 软件，将模型导入到水动力模块中进行运动响应分析，得到目标渔船在不同波频下的附加质量和阻尼系数，以及各个波频和不同浪向角下的运动响应幅值算子等水动力参数，研究浪向角与波频对围网渔船运动响应的影响，为实船航行提供参考。

1 计算理论

波浪对船舶等海洋工程结构的作用主要分为四种：1)由于海水的粘性而引起的粘性效应；2)由于海水的惯性以及船舶的存在，使得船舶周围的流场速度分布发生变化而引起的附加质量效应；3)由于船舶自身对入射波浪作用而产生的散射效应；4)由于船舶本身的相对高度较大，船舶与自由表面接触扰动了原波动场的自由表面而产生的自由表面效应。由于水的粘性对波浪影响是相当小的，在讨论波浪运动时，仅限于不可压缩理想流体且运动是有势的,并且在解拉普拉斯方程时用到的运动学、动力学条件方程式的结果不能预先确定且为非线性，为此进一步引进微波幅假定(波浪的振幅A 比波长L 为小量)，使得自由表面上的边界条件线性化，从而在求解上较为简单[5]。根据线性水波理论[6]可以，得到规则深水微幅简谐波的波长L、圆频率ω、波速C 与波浪周期T 之间的一般关系。

船体受到因流体引起的附加质量效应作用[7]，而粘性效应的影响较小在本文中忽略不计，因此计算出流场速度势是解决流体动力问题的关键所在。如果入射波的波高远小于波长，只考虑一阶速度势，忽略高阶速度势,则问题可通过线性势流理论进行简化。定义φ0为平面内的入射势，具有固定的方向和波期，是已知的。无限水深条件下，φ0可写作[8]：

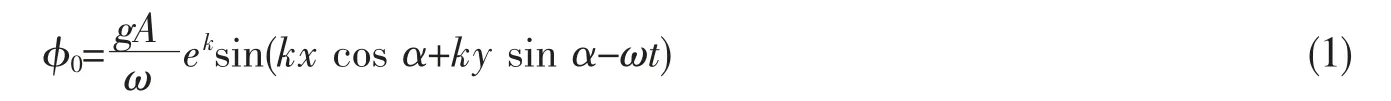
式中：g 为重力加速度；A 为入射波振幅；ω 为入射波波频；k 是入射波波数；α 表示入射波方向。在得到流场入射势后，根据线性化的伯努利方程，可得到P(x,y,z,t)：

波浪力的计算按照其尺度大小的不同可以分为两种：1)与入射波相比，尺度较小的结构，如海底输油管道，此类结构的存在对波浪运动不会造成显著影响，波浪对结构的作用主要为粘性效应和附加质量效应；2)而随着结构尺度相对于波长比值的增大，例如船舶、海洋平台，此类尺度较大的结构自身的存在对波浪运动有显著影响，对入射波浪的绕射效应以及自由表面效应必须考虑，此时要采用势流理论计算波浪力f。

其中f1为浮力(矩)，与结构重力和系泊回复力平衡；f2和f3分别由入射势和绕射势产生；f4为回复力，由静水力提供。

2 计算模型

2.1 围网渔船主要尺度

该船为单层底、单甲板、钢质飞剪型首、方型尾围网渔船，总长59 m，垂线间长48.5 m，型宽8.3 m，型深4.3 m，设计吃水3.45 m，设计排水量1 343 t，设计航区为中国远海，淡水舱分别布置在艏艉，全船共设6个燃油舱，3 个冷藏鱼舱。

2.2 船体水动力模型

由于船体结构复杂，围网渔船设备多而繁杂，在建模过程中，着重考虑大设备，将一些质量较小的设备适当忽略或者合并到大设备中去，以简化建模，节省计算资源。模型坐标原点位于船体基平面、中线面和船尾垂向界面的交点处，X 轴正向指向右舷，Y 轴正向指向船艏，Z 轴正向指向上方，基线定义为与Y 轴重合的直线。

目标渔船的运动响应分析还需要建立以下几种有限元模型[9]：

1）湿表面模型，如图1(左)所示。主要用于计算基于势流理论的水动压力、附加水质量和势流阻尼系数；

2）结构模型，如图1(右)所示。用于定义船体舱室的划分以及舱容；

3）质量模型，主要用于模拟围网渔船的质量分布，在水动力分析模块中可以选择从结构模型中导入质量，也可以选择根据浮心来定义船舶重量等。

图1 湿表面模型(左)与结构模型(右)Fig.1 Wet surface model (left) and Structural model (right)

将以上几种模型组合得到水动力模型，在施加环境载荷后，进行目标渔船的运动响应分析。船舶在海水中有6 种运动形式，分别为X 轴向横荡(sway)、Y 轴向纵荡(surge)、Z 轴向垂荡(heave)、X 轴向横摇(roll)、Y轴向纵摇(pitch)和Z 轴向艏摇(yaw)[10]。目前的研究表明，复杂的波浪可理解为无限多个振幅、波期、初相位不等的简谐波叠加而成。围网渔船的随机波浪响应也可理解为对各规则波响应的线性叠加，可以通过6 个方向上波浪运动的线性传递函数求解船舶运动[11]。

3 运动响应分析

3.1 附加质量和势流阻尼计算

船舶的水动力特征参数包括附加质量、势流阻尼、回复力矩[12]等，这些特征对船舶的运动响应和荷载响应起着决定性的作用。运用软件中的水动力模块进行计算，得到目标渔船在深水环境下附加质量和势流阻尼随波浪周期变化的曲线。通常，附加质量和阻尼系数都可以用一个6×6 的矩阵来表示。对目标渔船的水动力特性起决定性作用的是位于附加质量矩阵和阻尼系数矩阵主对角线上的各个值，以横荡和艏摇为例，结果如图2-3。

图2 横荡附加质量、势流阻尼随波浪周期变化Fig.2 The additional mass and potential flow damping of swaying with the wave period

图3 艏摇附加质量、势流阻尼随波浪周期变化Fig.3 The additional mass and potential flow damping of yawing with the wave period

附加质量随波浪周期起伏变化，随着波浪周期的增加呈现先急剧增大到极值后又缓慢减小的趋势。在横荡状态下，船体在波浪周期为7 s 时附加质量达到最大，为1.68×106kg；在艏摇状态下，船体在波浪周期为7 s 时附加质量达到最大，为1.83×109kg。由于在高频波浪下，船体与海水的接触面积小且变化快；而在低频波浪下，船体稳定航行，与海水的接触面积变大且变化小，因此呈现先急剧增大到极值后又缓慢减小的趋势。

势流阻尼随波浪周期起伏变化，随着波浪周期的增加呈现先增加再快速减小至一个小量的趋势。原因同附加质量相同，均是在高频波浪下，船体与海水的接触面积小且变化快；而在低频波浪下，船体稳定航行，与海水的接触面积变大且变化小。在横荡状态下，船体在波浪周期为4 s 时势流阻尼达到最大，为1.5×106kg·m·s-2；在艏摇状态下，船体在波浪周期为4s 时势流阻尼达到最大，为1.46×106kg·m·s-2。

3.2 运动响应分析

为了研究不同浪向角、波频对围网渔船运动响应的影响，同时考虑到渔船自身液舱对其运动影响较小，在忽略液舱晃荡的前提下，选取一系列规则波，波浪周期为2～25 s，间隔1 s，浪向角从船尾到船首方向依次选取0°～180°，中间依次间隔15°，对目标渔船进行运动响应分析，得到目标渔船在六种运动方向上的运动响应幅值。浪向角的定义如图4。

从图5 可以看出，在不同的浪向和浪频作用下，渔船的横摇运动响应幅值明显不同。除了浪向为0°和180°时，渔船横摇幅值对浪频不敏感，在其他浪向上，渔船横摇幅值均随着浪频的增大先变大后变小。具体来看，当波浪频率在0.8～1.1 rad·s-1范围时，除浪向为0°和180°，其他浪向对渔船的横摇响应都达到该浪向下的最大值，说明该频段对渔船横摇能产生谐摇反应。从浪向角的变化来看，横浪对渔船的横摇运动影响最大，随着浪向与舯纵剖面的夹角减小，横摇运动响应的峰值也随之下降。

图6 显示了渔船在不同浪角和浪频下的垂荡响应结果。可以看到，渔船的垂荡运动响应在低频率下相对较大，并随着频率的增长呈逐渐上升趋势。在浪频为1.25 rad·s-1附近处，船体的垂荡响应达到最大，之后随着波频的增加运动幅值渐渐减小。但是也可以看到，当浪向角在60°～105°时，船体纵荡响应出现的峰值的会适当后移。

图7 所示，当浪向角为0°和180°时，渔船的横荡响应幅值不受浪频影响。在其他浪向角下，渔船的横荡运动响应和垂荡时结论相似，即在低频波下响应幅值较大，并随着频率的增长呈逐渐上升趋势。并且，这两种运动响应的峰值也非常接近，只是横荡响应峰值的0.8～1.1 rad·s-1浪频范围内。

图4 浪向角的定义Fig.4 Definition of wave angle

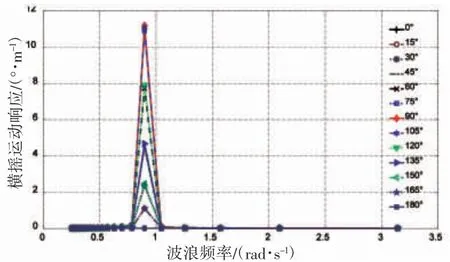
图5 各波浪角下横摇响应幅值随波浪周期变化Fig.5 The amplitude of roll response at each wave angle vary with the wave period

图6 各波浪角下垂荡响应幅值随波浪周期变化Fig.6 The amplitude of heave response at each wave angle vary with the wave period

图7 各波浪角下横荡响应幅值随波浪周期变化Fig.7 The amplitude of sway response at each wave angle vary with the wave period

图8 和图9 分别为各浪向角下渔船纵摇和艏摇响应随浪频变化的情况。可见，相对于上述三种运动响应，渔船的纵摇和艏摇响应幅值都非常小，因此不再重点分析。

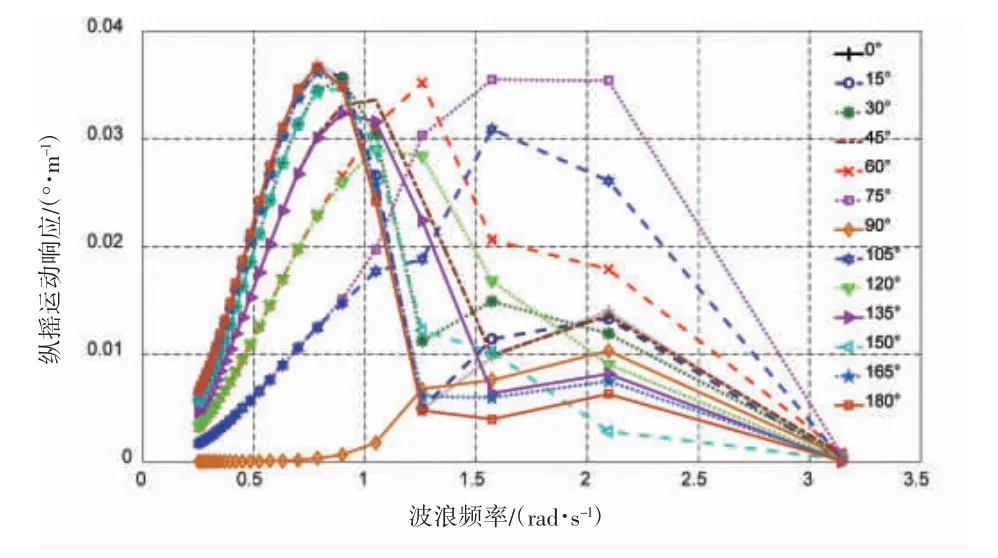
图8 各波浪角下纵摇响应幅值随波浪周期变化Fig.8 The amplitude of pitch response at each waveangle vary with the wave period

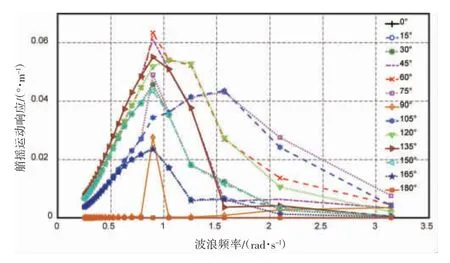
图9 各波浪角下艏摇响应幅值随波浪周期变化Fig.9 The amplitude of yaw response at each wave angle vary with the wave period

从图10 中可以看出，浪向角的不同，对渔船的纵荡响应影响差距较大，即入射角度与舯纵剖面的夹角越小，响应幅值越大，且纵荡响应随着波频的增加逐渐减小。

综上所述，目标渔船除纵荡运动外，其他五种运动响应均随波频的变大呈现先增加后减小的趋势，且在低频波浪上的重合度较高。同时，渔船运动响应与浪向角有关，不同的浪向角之间对运动响应的影响差距较大。不管是横荡、横摇、艏摇还是纵荡，浪向角对渔船运动响应的影响都可以分以下几种组合：①0°、180°；②30°、150°；③60°、120°以及④90°。同组合内的不同浪向的运动响应重合度相对较高，尤其是在低频波浪下，而不同组间的浪向造成的运动响应又极其不同。

3.3 运动响应对比

选择了4 组对渔船运动响应较大的浪向角作对比，其中垂荡、横摇与横荡是影响渔船水动力性能的主要运动形式。

图10 各波浪角下纵荡响应幅值随波浪周期变化Fig.10 The amplitude of surge response at each wave angle vary with the wave period

图11 45°浪向角下垂荡、横摇、横荡运动响应对比Fig.11 Motion response comparison at 45° wave angle

图12 75°浪向角下垂荡、横摇、横荡运动响应对比Fig.12 Motion response comparison at 75° wave angle

对比图10-14 可见，无论在哪个入射波浪角下，横摇都是最影响渔船性能的运动形式。同时，在航行或捕捞过程中，需要避免0.8～1.1 rad·s-1角频率的波浪，保证渔船稳性。

图13 90°浪向角下垂荡、横摇、横荡运动响应对比Fig.13 Motion response comparison at 90° wave angle

图14 105°浪向角下垂荡、横摇、横荡运动响应对比Fig.14 Motion response comparison at 105°wave angle

4 结语

本文根据深水微幅简谐波理论、势流理论，对舟山某一投入使用的远海航区钢质围网渔船进行了运动响应分析，通过数值模拟计算出目标渔船的附加质量、势流阻尼、运动响应幅值，预报了目标渔船在六个运动方向下的水动力特征系数，分析了浪向角和波频对渔船运动响应的影响，得出以下结论：

1）浪向角和波频都是影响渔船运动的主要因素。横摇运动响应相对其他几个方向上的运动响应幅值最大，是渔船需要特别注意的一种运动形式。

2)目标渔船在高频波浪下的水动力特征系数变化都较大，而在低频波浪下都趋于一种稳定的形式，变化较小。

3)通过对比，从六个运动方向响应图中可以得出，目标渔船在设定环境参数下的运动响应幅值处于～个正常水准，但为了保证渔船的安全，在航行过程中需要特别避免0.8～1.1 rad·s-1波频下的横浪，以排除横摇运动对全船稳性的负面影响。在该特征波频段减小浪向角，可以大大减小船舶横摇响应，从而保证船舶的航行安全。