基于粗糙集神经网络的房产税基批量评估研究
王阿忠 李 倩
(福州大学经济与管理学院, 福建福州 350108)
引言
房产税赋是房地产行业重要的税制改革,有助于促进地方政府构建“重保有、轻流转”的财税结构,可培养地方长期稳定的税种,建立新的财政收入来源,分化地方政府对土地财政的依赖,对构建房地产市场健康稳定发展的长效机制具有重要意义。目前而言,全面开征房产税关键问题之一就在于构建一个切实可行且公允公正的房产税基评估体系。根据世界各国的实践经验,税基应选定为房地产的评估价格。房产税税基评估量大面广,评估时点要求一致性。与传统的单宗评估相比,批量评估不仅效率高、易于实现评估结果的透明化和一致性,还更能体现客观性和公正性。因此,批量评估当之无愧地成为房产税税基评估方法的首选。批量评估是在三大基本评估方法(成本法、市场法和收益法)的原理基础上,结合财产特征数据,运用数理统计理论建立评估模型,并以计算机信息技术、GIS地理信息技术为辅助手段,对大量应税住宅进行评估的方法。其实质是对大量处于一定条件的住宅样本建模,并利用模型对任何符合模型要求的目标住宅进行估价。
国内外学者在税基批量评估领域理论方法的研究已经有了丰硕成果,纵观国内外批量评估研究,学者们通过理论阐述和实证分析对批量评估的方法进行了全面探讨,在实际评估中使用较多的是特征价格模型,或是在特征价格模型的基础上进行创新融合的方法和技术,此外还有因子分析法、主成份分析法和灰色聚类法等方法。特征价格模型的理论虽然较为简单易懂,但在应用中也存在一定的局限性,例如住宅价格与其特征变量之间关系错综复杂,具有不确定和非线性等特性,很难用某种确定的数学公式模拟出二者之间的关系。而且特征价格模型在运行中有可能会误删掉那些重要却不显著的变量。另外使用的一些技术模型不具有实用性,或是把简单的问题复杂化,不便于评估人员的操作。
相比之下,人工神经网络有非线性动态模拟的特点,它不需要设计任何数学模型,只基于过去的经验来学习,可以发现隐藏在评估案例背后的规律,即价格与其影响因素之间复杂的关系,并能够将这个信息存储和推广泛化,适合在住宅价格批量评估中的应用。Kathmann Ruud M将神经网络模型用于市场分析法中。[1]Peterson S,Flanagan A B通过比较神经网络与特征价格模型,认为相对于线性的特征价格模型,神经网络模型的错误率低,对于模型外样本有更高的评估精度,在价格波动剧烈的环境下有更强的泛化能力。[2]Kempa Olgierd,Lasota Tadeusz将神经网络与模糊系统相结合用于房地产的评估。[3]Jingjuan Guo,Shoubo Xu在运用成本法评估房地产时使用到BP神经网络进行校准。[4]国内学者申玲等首次将人工神经网络理论引入我国的房地产评估领域,取得了较好的效果。[5]吴劲军和李菊等提出了BP神经网络区间估算法,并验证BP神经网络模型用于房地产批量评估的合理性。[6][7]汪瑞运用BP神经网络方法构建房地产评估价格与相关影响因素之间的映射关系,通过优化BPNN的权值和阈值来提高BPNN的收敛速度,解决算法陷入局部极值点的问题。[8]在房地产价格影响因素研究中运用MIV-BP型神经网络模型,可以大大减少各影响因素对其影响程度评价的主观性。[9]考虑空间自相关性的住宅价格神经网络建模,构建了空间型BP神经网络模型,在价格评估实证分析中取得了良好效果。[10]
但是,在进行影响因素指标体系的初选时,为了更加全面地反映房地产价值的信息,通常会尽可能多地选取指标变量,当变量之间存在较多的冗余信息时,神经网络可能出现在训练阶段收敛困难、泛化能力低、预测精度不理想等问题。[11][12][13]粗糙集(RS)理论能够在保证信息分类能力不变的前提下对变量间的冗余信息进行约简,但其对噪声敏感且泛化能力弱。Kostke Bozena将粗糙神经网络模型应用于音乐大厅中音质的评价研究。[14]Ahn BS等用粗糙神经网络的方法用过去的财务数据来预测公司破产的可能性。[15]在国内也有很多的研究人员从事着粗糙集神经网络模型的研究。张兆礼等将粗糙神经网络模型用于数据融合的研究中。[16]陈伟达将粗糙神经网络模型用在税收预警系统中,得到了较满意的效果。[17]许多的研究表明,将RS理论与BP神经网络这两种方法结合起来使用,可以实现优势互补,适合在批量评估中使用。
一、本文的理论基础
(一)粗糙集
波兰理工大学的Pawlak Z教授在1982年提出了粗糙集理论,它是一种研究不精确、不确定性、不完整信息的数据分析理论。粗糙集的主要思想是利用已知的知识库,在维持系统分类原有能力的前提下,通过对数据属性进行约简,剔除冗余成分,导出问题的决策和分类规则。[18]在使用时不需要提供求解问题时所需处理的数据集合之外的任何先验知识。概率统计、模糊集等也是处理不确定信息常用的方法,但是它们需要概率分布、模糊隶属函数等附加信息和先验知识,粗糙集是通过对数据本身进行分类处理来发掘隐含知识的,所以对问题的描述和处理是比较客观的。
(二)BP神经网络
BP神经网络是一种采用反向传播算法的前馈型神经网络,理论上,多层的BP网络能够逼近任意非线性连续函数。结构上包含一个输入层、一个输出层及一个或多个隐含层,每层都由若干个节点(神经元)构成。BP神经网络学习算法的中心思想是通过调整输入层与隐含层、隐含层与输出层的权值、阀值使得网络总误差最小,其基本原理是梯度最速下降。网络学习过程包含了信息的正向传播和误差反向传播两个阶段。信息流经逐层计算传出网络,通过与期望输出的比较,计算出误差信号,然后使误差信号反向传播,从输出层经各个隐含层并逐层修改连接权值。如此反复,直到误差降低到期望的范围内,训练过程结束。
本文选用的市场比较法是直接依赖于市场资料以及房屋的客观条件,在用这种方法进行房价评估时,需要对交易情况、区域因素、个别因素等进行调整修正。人为进行评估时,往往都是凭借经验确定各因素的权重,而神经网络是通过样本学习,根据样本映射出各影响因素之间的关联。评估过程就是把用来描述某一地区住宅评估对象特征,即影响住宅价格的因素信息,作为神经网格的输入向量,将成交价格作为神经网络的期望输出。选取足够数量的训练样本,通过对影响因素和房产价格的训练学习,用分布在网络内部的连接权值来表达所学习的价格评估知识,对它们不断地进行修正,直到满足设定的误差精度。最后得到一组权值和阈值就是网络经自适应学习所得到的正确内部表示。训练完毕后,即可用训练好的模型对该地区的其它房屋价格进行评估。
(三)基于粗糙集BP神经网络的批量评估模型的理论架构
目前粗糙集神经网络在许多领域已经得到了成功的应用,有了很成熟理论和实践基础,近年来也开始逐步在房地产领域中得到了应用。本文将粗糙集神经网络模型用于房产税税基批量评估中的理论架构为:首先应用粗糙集作为前置系统对输入的影响因素指标进行预处理,在保证信息完整的情况下删除冗余属性;然后以约简后的、解释能力强的关键影响指标作为BP神经网络的输入,对网络进行训练和建模,最后利用训练好的模型对住宅价格进行批量评估。基于粗糙神经网络的房产税税基批量评估模型架构如图1所示。
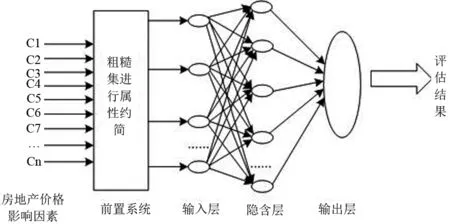
图1 粗糙神经网络房产税税基批量评估模型架构
理论上构建房产税税基批量评估模型主要包含4个阶段:
(1)数据预处理。量化样本中的影响因素,将量化后的影响因素值作为粗糙神经网络模型的输入数据,样本的成交价格作为网络的输出。
(2)利用粗糙集进行属性约简。由于粗糙集基于集合论,所以只能处理离散型的数据。首先要将连续的属性值做离散化处理,其次利用粗糙集方法将输入的属性全集约简为最小属性集。
(3)对BP神经网络进行训练。首先根据约简后的属性集合,确定神经网络的层数、每层的节点数、传递函数。其次以未经离散化的数据作为神经网络的输入数据,并对其进行归一化处理。再次,设定误差值、最大学习次数等系统参数,对阀值、连接权值等进行初始化处理。对网络进行训练,直到全局误差小于预定误差时,学习结束。
(4)用训练好的BP神经网络对待估住宅进行价格预测。
二、粗糙集神经网络批量评估模型的构建
(一)评估指标体系的建立
影响住宅价格的因素主要分为三大类,在总体上影响某地区住宅的价格水平,我们称之为一般因素;直接影响到某一具体住宅价格,称为区域因素和个别因素。住宅价格是在其交易时间内各种因素综合作用的结果,由于在较短时间内,宏观政策环境、经济发展等一般因素都处于比较稳定的状态,其影响基本可以忽略,因此本文仅考虑区域因素和个别因素对商品住宅价格的影响。
通过对现有研究成果的借鉴总结和对实际情况的分析[19][20],选用建筑面积、楼层、总层、房龄、户型、容积率、绿化率、朝向、建筑类别、有无电梯、装修程度、物业管理、小区环境、车库配比率、交通便利程度、商服繁华程度、基础配套设施、生活配套设施、教育配套设施、间距等23个关键因素作为输入变量来建立住宅价格批量评估模型。
指标体系中既有定性指标又有定量指标,为了保证可比性,需要根据指标的特性通过多种手段将定性的指标做定量化处理,具体的量化方案如表1所示。

表1 指标量化方案
续表1
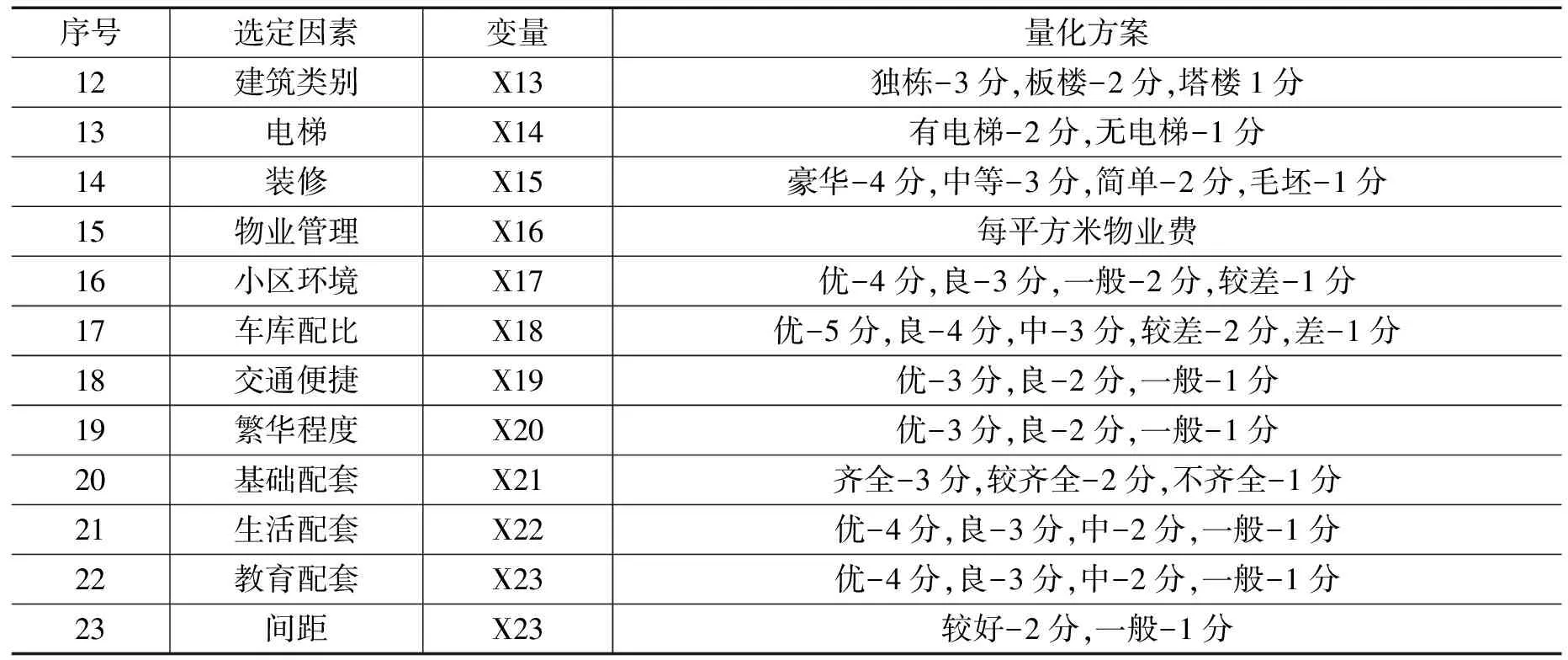
序号选定因素变量量化方案12建筑类别X13独栋-3分,板楼-2分,塔楼1分13电梯X14有电梯-2分,无电梯-1分14装修X15豪华-4分,中等-3分,简单-2分,毛坯-1分15物业管理X16每平方米物业费16小区环境X17优-4分,良-3分,一般-2分,较差-1分17车库配比X18优-5分,良-4分,中-3分,较差-2分,差-1分18交通便捷X19优-3分,良-2分,一般-1分19繁华程度X20优-3分,良-2分,一般-1分20基础配套X21齐全-3分,较齐全-2分,不齐全-1分21生活配套X22优-4分,良-3分,中-2分,一般-1分22教育配套X23优-4分,良-3分,中-2分,一般-1分23间距X23较好-2分,一般-1分
(二)模型的建立
1. 输入输出变量的确定
本文选用住宅的成交价格作为输出变量,将影响住宅价格的23个影响因素作为输入变量。
2. 属性约减
本文选用基于属性重要度的约简算法,基本思想是,首先得到属性核作为属性约简集的基础,然后计算属性的重要度,通过比较删除对价格影响微弱或是没有影响的属性。具体步骤如下:
第1步设R=Φ;
第2步∀α∈A,如果ind(A-{α})≠ind(A),则R⟸R∪{α};
第3步core(A)=R即为所求的核;

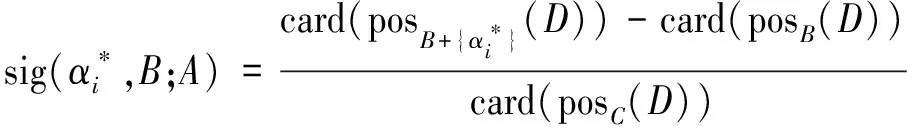
(1)
第5步通过比较,删除重要度较小的属性,求得约简属性集。
3. BP神经网络的设计
(1)神经网络的层数。BP神经网络一般是由一个输入层、一个输出层,再加若干隐含层构成。增加隐含层的数量可以使得网络的处理能力变强,但也会导致训练变得复杂。众多实验表明,在不限制隐层节点数量的前提条件下,含有一个隐含层的BP神经网络是能够逼近任意一个非线性函数的。因此,本文确定采用三层的BP神经网络来构建批量评估系统,通过增加隐含层节点数的方式来降低误差。
(2)各层节点数。输入节点数与输出节点数是由问题本身决定的,根据房产价格批量评估原理的特点容易判断出:输入层接受外部数据的输入,节点数取决于输入向量的维数,因此节点数等于经过粗糙集约简后的属性个数;输出层输出的是房产的评估价格结果,所以输出层设定为一个节点。
相比与输入、输出层,隐含层节点数的确定是比较复杂的。隐含层神经元数目对整个网络的非线性映射能力影响巨大,节点数不足会导致训练失败,学习过程不能收敛;但是如果在隐含层选用过多的节点,这会导致过度学习,泛化能力变差等情况。一般可以通过经验公式来确定隐含层节点数的大概范围,然后用试凑法确定最佳节点数,如公式2所示:
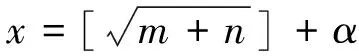
(2)
其中:x为隐含层节点数,m为输入节点数,n为输出节点数,[x]为取整函数,α为常数。在用试凑法求取最佳节点数时,首先设置较少的隐层节点训练神经网络,然后通过调节α值逐渐增加隐层节点数,最后确定网络误差最小时对应的隐含层节点数。
(3)节点间的连接。本文采用BP神经网络模型,上一层神经元节点只接受下一层神经元节点的输入,同层的节点之间不存在连接,反馈连接网络与层内有互联网络。
(4)传递函数。BP算法要求转移函数处处可微,通常采用Sigmoid函数,Sigmoid函数的输出接近生物神经元信号的输出形式,能够很好地拟合非线性关系。
(5)学习算法。本文采用BP神经网络算法,并用动量-自适应学习速率调整算法对其进行优化。典型的三层BP神经网络结构如图2所示。
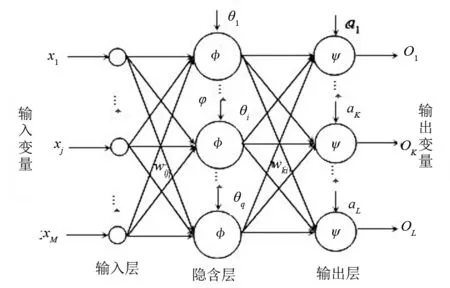
图2 BP神经网络结构
其中:xj表示输入层第j个节点的输入,j=1,…,M;
wij表示隐含层第i个节点到输入层第j个节点之间的权值;
θi表示隐含层第i个节点的阈值;
φ(x)表示隐含层的传递函数;
wki表示输出层第k个节点到隐含层第i个节点之间的权值,i=1,…,q;
ak表示输出层第k个节点的阈值,k=1,…,L;
ψ(x)表示输出层的传递函数;
ok表示输出层第k个节点的输出;
tk表示输出层第k个节点的期望输出。
1) 信息的正向传播过程
隐含层第i个节点的净输入si:

(3)
隐含层第i个节点的输出yi:
(4)
输出层第k个节点的输入netk:
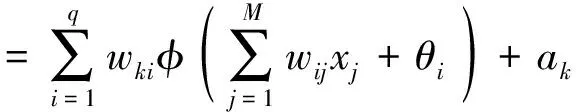
(5)
输出层第k个节点的输出ok
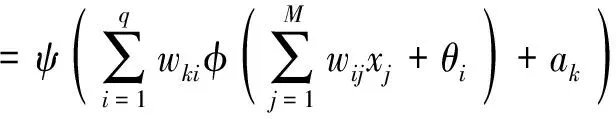
(6)
2)反向传播过程
误差的反向传播,即首先由输出层开始逐层计算各层神经元的输出误差,然后根据误差梯度下降法来调节各层的权值和阈值,使修改后网络的最终输出能接近期望值。对于每一个样本p的二次型误差准则函数为Ep:

(7)
系统对P个训练样本的总误差准则函数为:
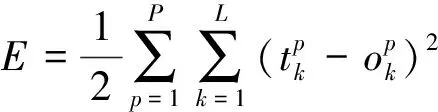
(8)
根据误差梯度下降法依次修正输出层权值的修正量Δwki,输出层阈值的修正量Δak,隐含层权值的修正量Δwij,隐含层阈值的修正量Δθi。

(9)
输出层权值调整公式:
输出层阈值调整公式:
隐含层权值调整公式:
隐含层阈值调整公式:
又因为:

(14)
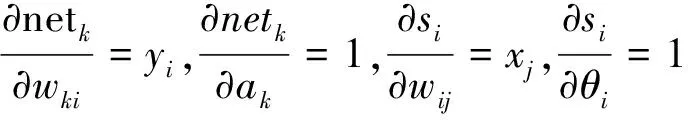
(15)
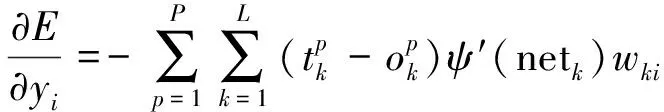
(16)

(17)

(18)
所以最后得到以下公式:
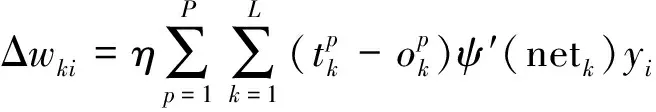
(19)
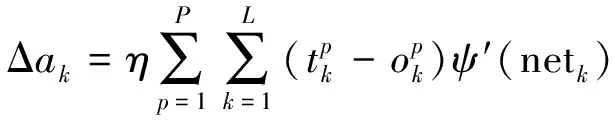
(20)
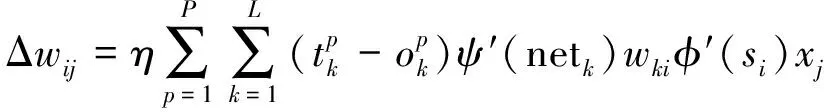
(21)
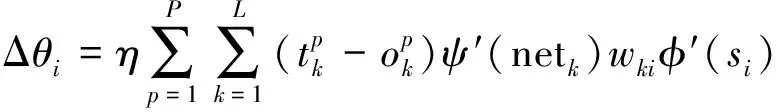
(22)
为了减小标准BP算法在学习过程中的震荡问题,可以在对连接权值和阈值进行调整时,将上一次权值调整量的一部分迭加到这次按误差计算的权值调整量上,作为本次的实际调整量,这就是附加动量法。公式如下:
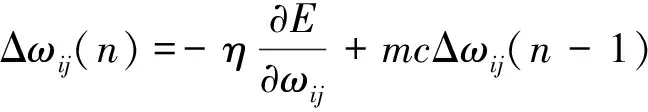
(23)
其中:η为学习率,mcΔωij(n-1)是动量项,mc为动量系数,通常0 自适应学习速率调整算法可以加快收敛速度,调整思路是:在网络收敛、误差修正方向正确的情况下,即在误差不断减小时,增大学习速率,以缩短学习时间;若误差修正方向错误,则减小学习速率,直到收敛。调整公式如下: (24) 其中:E(n)为第n步的误差平方和,kinc为学习速率增量因子,kdec是学习速率减小因子。 将两种算法同时使用,即动量-自适应学习速率调整算法。 (6)学习速率。学习速率的作用是不断调整权值、阀值,其值一般取0.01-0.1之间,本文设定为0.05。 (7)初始条件。初始权值在理论上可以任意选取,但BP算法对初始权值极为敏感,不同的权值导致不同的结果。初始权值过大的后果是加权后输入值会落到传递函数的饱和区,此时导数极小,从而引发权值的调节过程停滞。一般希望每个神经元的净输入都约等于零,这样就可以保证其输出在转移函数的中点附近,即函数变化最灵敏的区域,该区域训练速度最快。一般将初始权值设置为[-l,+1]区间的任意数。 (8)终止条件。除了在系统误差小于期望误差要求情况下能够结束训练之外,终止网络训练的条件还包括学习次数。本文将期望误差设置为0.0008,学习次数上限设置为10000次。 本文以福州市五四北板块的普通住宅为研究对象,板块是指同一供求范围内类似的住宅。共取得15个普通住宅小区132个完整有效的住宅数据样本,选取其中122个作为建模样本,剩余10个作为模型的检验样本。样本来自二手房中介公司的真实成交实例,交易时间集中在2015年6月到2015年12月。 用k-means聚类方法和等距离聚类方法对部分连续属性进行离散化处理,然后对新的决策表进行属性重要度分析。在本文中,论域U=待训练样本;决策属性D={总售价};条件属性集C={α1,α2,…,αi}={面积,楼层,……,间距},利用ROSETTA软件。 首先,求取C相对于D的核corec(D)。由理论分析可知,对于每一个属性αi,若存在posind(C)(D)=posind(C-ai)(D),则可认为αi在C中对D是不必要的,反之则认为αi在C中对D是必要的,根据相对核的定义,可得: corec(D)={面积、楼层、装修、间距} (25) 经过计算每个非核属性的重要度如表2所示。 再次,确定约简属性集。从表2可以看出客厅、容积率、建筑类别、基础配套这4个变量的属性重要度相对较小(这与同一住宅板块中规划趋同导致4个变量相近有关),近似等于0,说明这些指标在同板块住宅价格批量评估中的作用不明显,是冗余的评估指标,可以剔除。其余指标明显大于0,它们在价格评估中起到重要作用,因此最后确定的条件属性集={面积,楼层,总层,房龄,室,厨,卫,绿化率,朝向,电梯,装修,物业,小区环境,车库配比率,交通便捷程度,繁华程度,生活配套,教育配套,间距},把它们作为神经网络的输入层结点。 表2 非核属性的重要度 本文使用MATLAB神经网络工具箱完成对BP神经网络的训练和学习,对数据的归一化以及反归一化也包含在程序中。将122组未经过离散化处理的样本作为训练样本,根据属性约简的结果,BP神经网络的输入层节点数为19,输出层节有一个节点即住宅的评估价格。根据经验公式以及反复调试,最终确定的隐含层节点是24个,构建的3层BP神经网络结构为19-24-1。 设学习速率r=0.05,动量因子为0.9,误差0.0008,最大训练次数为10000次,对训练样本进行训练,从图3中可以看出,迭代到2246步时网络收敛的稳定性能达标,训练完毕,然后利用训练好的网络对10组测试样本进行评估。最后与未经过粗糙集属性约简的神经网络模型预测结果进行了比较,两种模型的评估结果与真实价格的比较见表3和图3。 从表3和图3可以看出,RS-BPANN与BPANN模型都能较好地评估住宅价格,它们与真实价格的变化趋势一致。但是前者的预测误差更小,且在训练过程中用时更短(图4)。说明利用粗糙集对BP神经网络进行优化是有意义的。 图3 RS-BP神经网络训练误差变化曲线 表3 RS-BPANN模型预测值、BPANN模型预测值与实际值的比较 图4 RS-BPANN模型预测值、BPANN模型预测值 与实际值的比较 神经网络能够处理房产价格与影响因素之间复杂的非线性关系,但是存在网络冗余这个瓶颈,本文将粗糙集与神经网络结合使用,粗糙集可以约简剔除冗余属性,减少神经网络的冗余程度,同时也为数据收集工作减轻负担。结果表明采用粗糙神经网络模型进行房产税税基评估是有效、可行的,能够为房产赋税中税基的批量评估实施提供帮助。 注释: [1] Kathmann R.M.,“Neural networks for the mass appraisal of real estate”,Computers,EnvironmentandUrbanSystems,vol.17,no.4(1993),pp.373-384. [2] Peterson S., Flanagan A.B.,“Neural network hedonic pricing models in mass real estate appraisal”,JournalofRealEstateResearch,vol.31,no.2(2009),pp.147-164. [3] Kempa O., Lasota T., Telec Z., et al.,“Investigation of bagging ensembles of genetic neural networks and fuzzy systems for real estate appraisal”,IntelligentInformationandDatabaseSystems,2011,pp.323-332. [4] Guo J., Xu S., Bi Z.,“An integrated cost-based approach for real estate appraisals”,InformationTechnologyandManagement,vol.15.no.2(2014),pp.131-139. [5] 申 玲、唐安淮:《基于BP神经网络的房地产市场比较法价格评估》,《系统工程理论与实践》1998年第5期。 [6] 吴劲军:《房地产估价研究:BP 神经网络区间估算法》,《统计教育》2004年第5期。 [7] 李 菊、杜 葵:《BP神经网络在房屋批量评估中的应用》,《价值工程》2015年第3期。 [8] 汪 瑞:《房地产评估的BP神经网络模型构建》,《山东农业大学学报》2016年第6期。 [9] 武田艳、占建军、严 韦:《基于MIV-BP型网络实验的房地产价格影响因素研究》,《数学的实践与认识》2015年第18期。 [10] 池 娇、焦利民:《住宅房地产价格评估的空间型BP 神经网络模型》,《地理空间信息》2017年第2期。 [11][16] 张兆礼、孙圣和:《粗神经网络及其在数据融合中的应用》,《控制与决策》2001年第1期。 [12][17] 陈伟达:《粗糙人工神经网络在税收预警系统中的应用研究》,《东南大学学报》(哲学社会科学版)2004年第1期。 [13] 宋李俊、赵 虎、周康渠等:《基于粗糙小波神经网络的客户协同供应商选择过程研究》,《计算机集成制造系统》2014年第12期。 [14] Kostek Bozena, Czyzewski A.,“Representing musical instrument sounds for their automatic classification”,JournaloftheAudioEngineeringSociety,vol.49,no.9(2001),pp.68-785. [15] Ahn Byeong Seok, Cho Sung Sik, Kim Chang Yun.,“The integrated methodology of rough set theory and artificial neural network for business failure prediction”,Expertsystemswithapplications,vol.18,no.2(2000),pp.65-74. [18] Pawlak Z.,“Rough sets”,InternationalJournalofComputer&InformationSciences,vol.11,no5(1982),pp.341-356. [19] 王立平:《我国房地产价格“稳健性”影响因素实证研究》,《管理世界》2013年第10期。 [20] 刘洪玉、杨振鹏:《基于主体变量的住宅价格批量评估》,《统计与决策》2012年第3期。
三、实证分析
(一)数据来源及变量分析
(二)输入变量约简
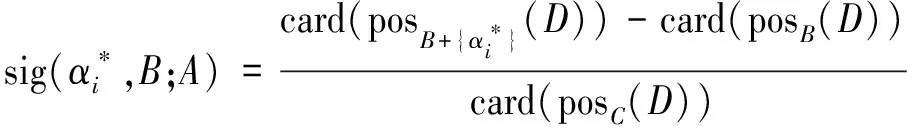

(三)神经网络估价
四、结语

