含运作时滞的供应链碳排放与成本投入研究

刘 虹 林 敏

(福州大学经济与管理学院， 福建福州 350108)

一、引言

近年来，随着全球气候变暖导致的自然灾害问题愈来愈严重，给人类的生活环境带来了严重的挑战。降低碳排放量成为世界各国政府、社会以及企业不得不解决的一个根本性问题。因此，众多国家为了限制二氧化碳的排放，纷纷出台了多项碳调控政策，加快投入运行碳排放交易体系，重点发展全球碳交易市场。国家层面的气候减排目标必将积极分解落实到社会层面众多企业的碳减排计划中，社会成员应积极承担减排责任。尤其对于制造业来说，不仅要创新其供应链绿色管理理念，更要重视碳减排技术的革新与改变。如菜鸟网络在实现电商物流绿色包装方面，实行全新的菜鸟共享物流模式，通过智能打包算法实现减量包装，提高纸盒利用率；推出共享快递盒、全生物降解袋以及无胶带纸箱等以达到节能降耗的减排目标，实现低碳经济。

在低碳经济发展背景下，供应链低碳减排问题主要集中于整体运营与生产运作等领域。从内部环境看，主要有供应链管理的定价问题、绿色策略以及不同决策博弈等[1][2][3][4]；从外部环境来看，更多集中于碳排放强度定量化管控与基于碳交易机制的定性化描述。[5][6][7][8]大量文献集中于政府碳政策调控角度展开，如Benjaafar等将碳排放问题纳入采购、生产和库存管理中研究，分析四种不同的碳排放政策对决策产生的影响[9]；Zhao等通过系统动力学模拟对比分析了政府直接补贴与优惠碳税率两种碳激励政策单独干预与联合干预对碳标签制度实施的影响变化[10]；周雄勇等从经济、人口、科技、能源和环境等多个系统角度构建系统间相互影响的节能减排系统动力模型，模拟不同的政策调控因子对节能减排的效果影响。[11]

更多的研究则从动态角度考虑供应链运作存在的滞后问题，如李翀、石永强针对动态框架下供应链运作特性提出了时间滞后因素，探讨时滞因素对供应链的影响[12][13]；王伟均等研究了需求信息滞后与库存牛鞭效应的关系[14]；陈东彦等假设碳减排效果存在时滞现象，在此背景下研究分散决策与集中决策的最优减排投入与定价策略，认为时滞存在一定阈值能使供应链趋于集中化决策。[15]

目前在供应链领域，对于时滞效应的研究大多集中于供应链网络系统的牛鞭效应影响，较少文献在研究供应链碳减排控制时考虑运作时滞因素。滞后时间对供应链碳排放策略及成本投入有较大影响，因此本文将时滞因素引入供应链低碳化研究中，研究各项延迟时间对供应链决策行为的影响。并在含运作时滞因素的供应链系统中引入两种不同的碳政策，通过系统动力学模拟分析不同的碳政策对供应链碳排放量与总成本的影响。

二、模型构建

本文考虑由单个制造商、零售商以及配送中心组成的供应链网络，构建系统动力学模型模拟运作过程发生时滞现象时对供应链主体的影响以及沿着供应链链路对供应链其他成员的影响变化。其中制造商、零售商以及配送中心由自身的运作行为产生相应的碳排放，如生产、运输和订购过程产生的碳排放，并且每个环节都有相应库存量而存在库存碳排放，每个供应链成员的运作行为产生相应的成本。

(一)系统因果图

根据本文的问题情境，采用系统因果图描述碳排放情形下供应链系统中各因素间的相互关系，如图1所示。图1呈现的多个反馈回路主要表明制造商(M)、零售商(R)以及配送中心(DC)在生产、销售和配送过程产生的碳排放量会增加各个子系统的碳排放总量，从而导致供应链总碳排放量的增多，而碳排放总量产生碳成本必然导致供应链总成本的上升。随着供应链盈利能力增加，进一步增强技术与管理水平的同时对生产、销售和配送过程的碳排放量起到一定的减缓作用。

图1 供应链碳排放系统因果回路

(二)系统流程图

在对图1系统因果图分析的基础上，利用系统动力学构建供应链碳排放系统的基本模型流图，如图2所示。在该模型中考虑生产延迟、配送运输延迟以及货物供应延迟，其中制造商库存由生产速率和取货速率决定，零售商根据市场的销售速率、订购周期及库存信息共同决定订购订单，而配送中心根据订单信息、取货速率来设置期望库存，并通过库存调整时间及时调整库存偏差。

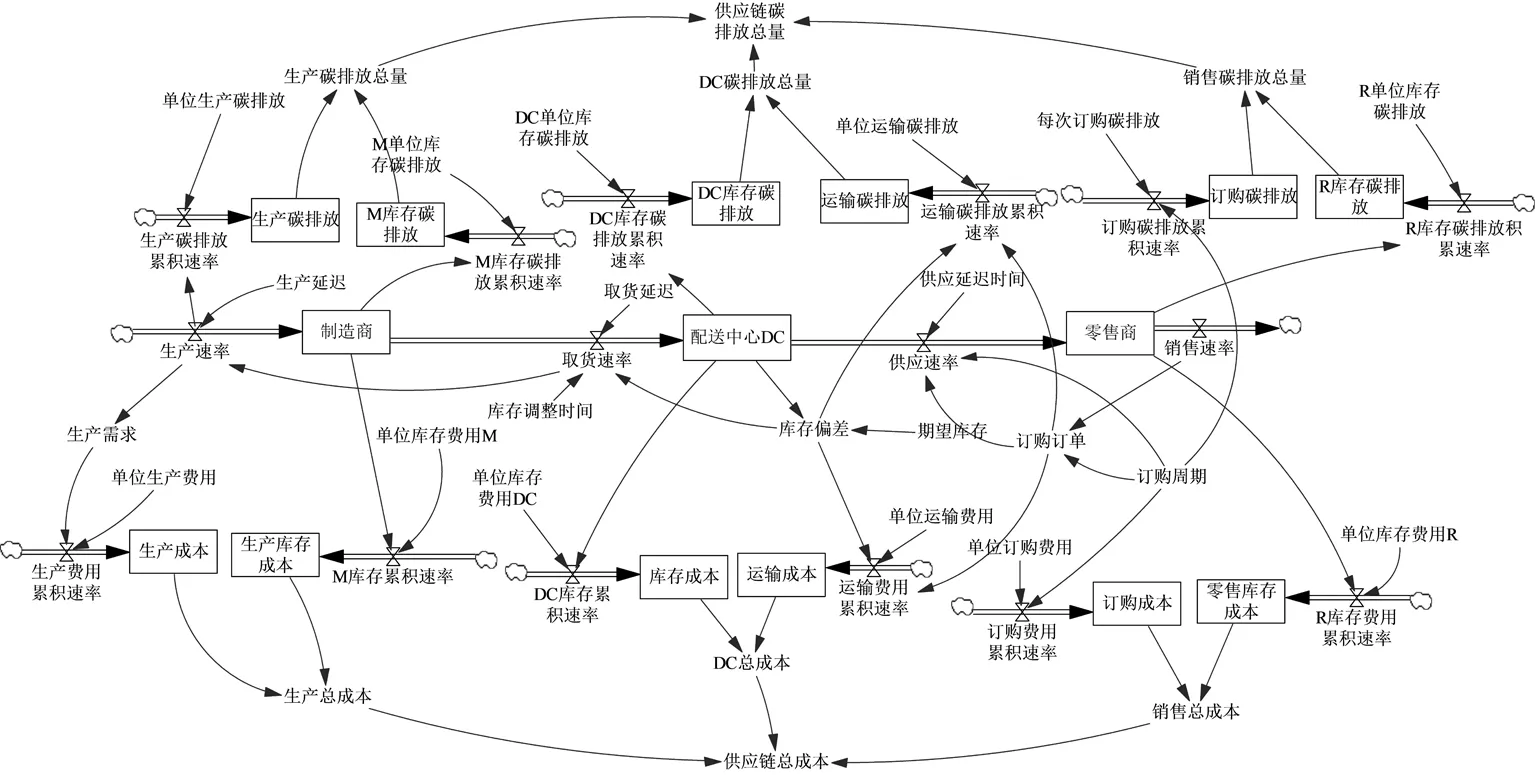
图2 供应链库存基本模型流程

(三)模型主要方程式

以下列出配送中心环节的主要方程关系(其他环节类似定义)，模型相关参数的设定如表1所示。

DC库存碳排放= INTEG (DC库存碳排放累积速率,0)

DC库存累积速率=配送中心DC*单位库存费用DC

运输碳排放= INTEG (运输碳排放累积速率,0)

运输碳排放累积速率=(库存偏差+订购订单)*单位运输碳排放

库存成本= INTEG (DC库存累积速率,0)

DC库存累积速率=配送中心DC*单位库存费用DC

运输成本= INTEG (运输费用累积速率,0)

运输费用累积速率=(库存偏差+订购订单)*单位运输费用

生产速率=SMOOTH(取货速率, 生产延迟 )

制造商= INTEG (生产速率-取货速率,1500)

取货速率=DELAY3(库存偏差/库存调整时间, 取货延迟 )

配送中心DC= INTEG (取货速率-供应速率,1500)

供应速率=DELAY3(订购订单*PULSE TRAIN(0, 1 , 订购周期 ,100) ,供应延迟时间)

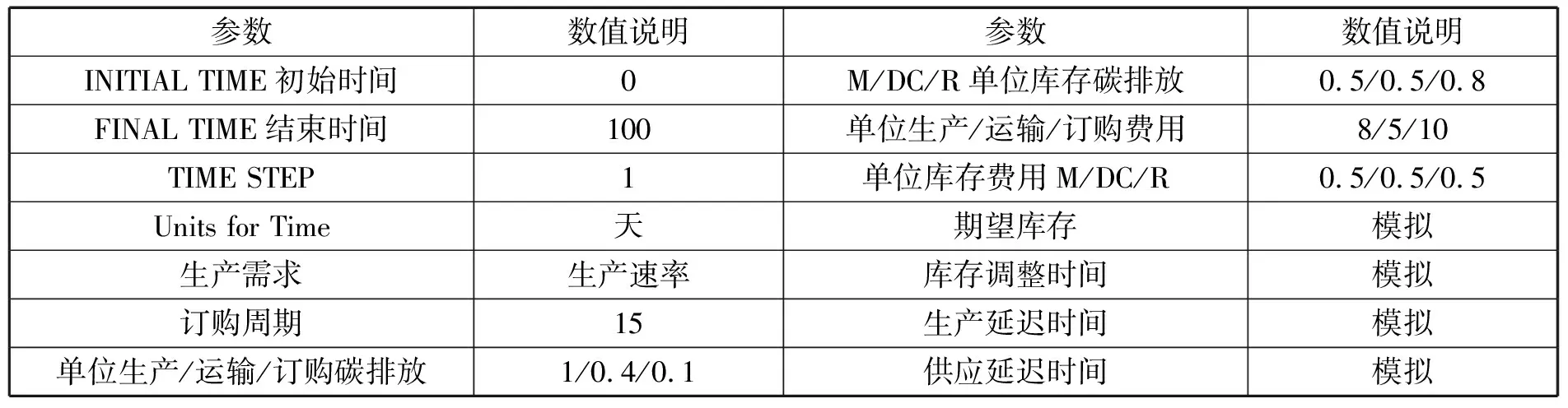
表1 模型相关参数设定

三、仿真结果与分析

(一)模型稳定性

为准确真实地表达供应链结构与运作过程，对模型稳定性进行检验，以验证系统动力学模型结构和行为的合理性。本文采取仿真步长为1、0.5和0.25的三种模式模拟仿真供应链碳排放总量与总成本的变化过程，其仿真结果见图3。由图3可看出，在大、中、小三种模式的时间步长下，整个仿真过程中其变化趋势几乎保持一致，说明该模型具有良好的稳定性。

(a)供应链碳排放总量

(b)供应链总成本

图3 系统模型对时间步长的变化灵敏度

(二)模型瓶颈分析

将设定的变量间关系和参数代入模型中，仿真周期以100天为一个周期，步长设为1，利用Vensim 软件模拟仿真供应链总成本和碳排放总量变化过程。本文通过对模型的瓶颈分析来找出整条供应链的敏感参数，进行敏感性分析寻求其最佳的取值点，进一步分析各因素对供应链总成本和碳排放量的具体影响。

1. 不同库存调整时间变化仿真及分析

供应链期望库存设置为3000，生产、取货、供应延迟分别为3、2.5、2.5 。通过对库存调整时间的敏感性测试后，选取库存调整时间为1.75、2、2.5、3进行对比分析，其仿真曲线如图4、图5所示，对应的数值如表2所示。

(a)制造商库存变化

(b)配送中心库存变化

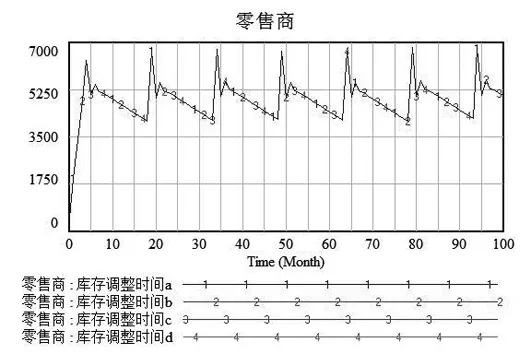
(c)零售商库存变化

图4 不同库存调整时间下供应链各成员库存变化

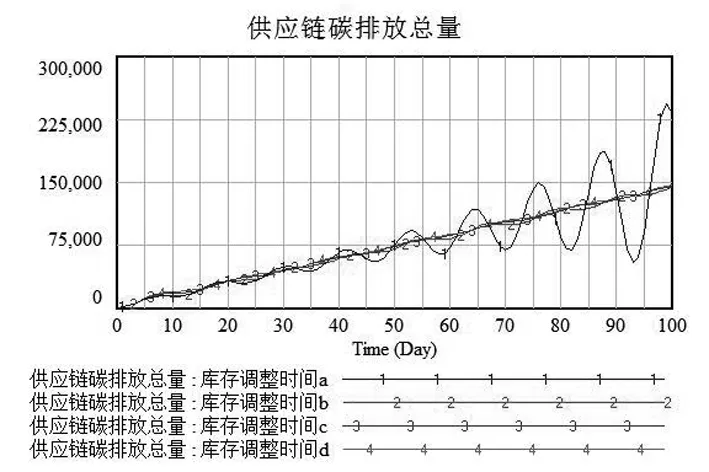
图5 不同库存调整时间下供应链碳排放总量和总成本变化曲线

表2 不同库存调整时间下的碳排放与成本

由图4可看出，制造商和配送中心的库存变化波动幅度几乎相同，而零售商处的库存不随库存调整时间变化，但零售商的库存会由于订货的周期性而呈现周期性变化。由表2可知，供应链各个环节中只有销售碳排放总量是一个固定值，说明库存调整时间的变化不影响销售环节，库存调整时间影响的是取货速率中具有相关关系的制造商和配送中心库存，进而影响供应链的碳排放总量和总成本。

从图5看出，供应链碳排放总量与供应链总成本随着库存调整时间的不同，二者曲线变化却相似(下文只列出碳排放总量曲线变化)。其中曲线1表示库存调整时间初始值取值为1.75时供应链碳排放总量与总成本的变化趋势，呈现波动上升趋势波动幅度相差较大，这是图4中制造商和配送中心的曲线1库存变化波动较大所导致的，因此整体上不利于供应链绩效优化。如果将库存调整时间进行逐渐增加，分别取值2、2.5、3进行仿真，图4中其曲线2、3、4的变化呈稳定趋势，其碳排放和成本变化趋势都呈现线性上升趋势，变化幅度不大且稳定。

此时，配送中心根据供应链碳排放量与总成本最小化的原则下，决策的库存调整时间为2天。可见库存调整时间并不是越小越佳，如若低于某一阈值不但不会降低成本与碳排放量反而会大量增加，这是由于时间的紧迫性会导致供应链运作需投入大量财力、人力才能达到时间的高效性。因此，供应链管理者需要根据供应链模型的结构和各影响因素的复杂性和合理性进行调整决策，寻求最佳的平衡点。

2. 各类延迟时间变化仿真分析

为进一步探讨模型中关键变量，本文设计了九组不同的变量取值，分成三组不同的实验对照比，其中期望库存设置为3000，库存调整时间为2，仿真周期以100天为一个周期，步长为1进行模拟仿真。分别讨论三种不同实验情况下供应链的碳排放总成本和碳排放总量，具体仿真如图6所示，具体数值如表3所示。

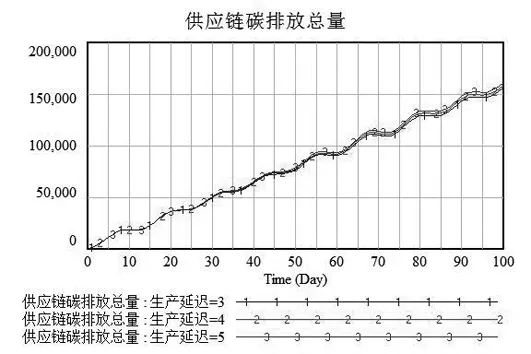
(a)生产延迟不同

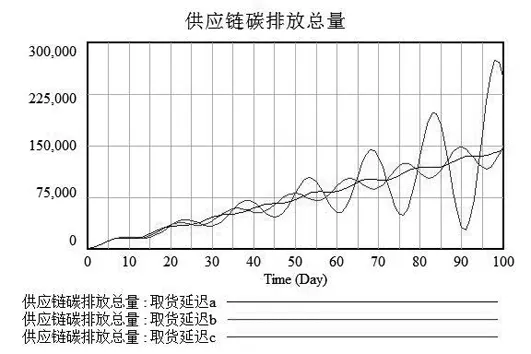
(b)取货延迟不同

(c)供应延迟不同

表3 时间延迟对供应链碳排放和成本的影响

由图6展现出各类延迟时间的不同对供应链碳排放总量的影响变化。生产延迟和供应延迟的模拟仿真曲线都呈现微波动上升趋势，而取货延迟曲线根据取值不同呈现出较大的差异变化，说明取货延迟对于该供应链结构来说是一个极其敏感的参数变量。结合图6的仿真曲线和表3的仿真数值结果进行具体分析如下。

(1) 第一组中生产延迟时间只影响生产环节的碳排放量，而配送中心与销售商的碳排放量保持不变。显然，生产制造时间由制造商管控，其滞后时间只会对制造商的库存造成较大影响，随之供应链碳排放总量与总成本都将随着生产延迟时间的增加而增加。可见，制造商对于生产环节的时间把控尤为重要，虽然由滞后时间带来的碳排放量和成本增长幅度不大，但当滞后时间较长时，会导致碳排放量难以管控，进而增加供应链的成本投入。

(2) 第二组中，制造商和配送中心的碳排放随着取货延迟时间的增加而增加，销售碳排放量是一个固定值，不受延迟时间的影响。而供应链总体碳排放随着取货延迟时间增加而增加，但供应链总成本却在取货延迟时间取3天时最低。这是由于取货环节不仅只考虑延迟时间，还考虑库存调整时间，二者参数的变化紧密联系制造商和配送中心的库存情况，合理的时间安排既能保证安全库存与订单完成，又能实现整体供应链绩效的提高。

(3) 第三组实验中，配送中心、销售商以及供应链碳排放与总成本随着供应延迟时间的增加而上升，但生产碳排放却与之呈相反变化，说明供应环节的延迟时间越长，反馈到制造商的订单时间则越迟，其生产制造环节投入产量越慢，所产生碳排放也越少。若从生产商角度考虑，会以延迟时间越长为最佳，但就总体碳排放量与成本投入来说，其供应延迟时间越低越好，即供应延迟时间取2.5天。在实际运作中，在碳排放量与成本投入双目标决策下，本实验中数值未达到最低状态，具有更大的进步空间。

总的来说，各类延迟时间对供应链总成本的影响比较复杂，需根据具体实际情况进行决策，但供应链中延迟时间的缩短有助于降低供应链的碳排放总量。因此，在供应链管理中，各环节都应当重视时间延迟的影响，根据实际情况积极采取措施，降低不必要的延迟时间，提高供应链的服务水平。

四、不同碳政策模型

以上探讨了各项运作时滞对供应链的碳排放与成本投入的影响。在此基础上，本文分别引入两个不同的碳政策，即碳交易政策与碳奖惩政策，探讨不同碳政策分别对含运作时滞供应链的碳排放与总成本产生的影响。

(一)碳交易政策

目前碳交易政策对碳市场来说是最常见的一种碳买卖方式，但根据市场碳配额分配方式不同会对碳政策的效果产生不同的影响。本文将通过模拟不同的碳配额免费比例与碳配额减少率，分析供应链碳交易变化情况。建立关于碳交易政策的模型如图7所示。

模型中关于碳交易政策的新增的主要变量方程为：

免费碳配额量=碳配额总量*碳配额免费比例；

碳配额总量= INTEG (-碳配额总量减少速率,15000)；

图7 碳交易政策下系统动力模型

1. 碳配额减少率的模拟仿真分析

在其他参数不变的条件下，模拟不同碳配额减少率下免费碳配额量的演化过程。如图8(a)所示，最初的供应链碳配额量是固定的，随着时间的推移和碳配额减少率的增加，政府分配的碳配额总量越来越少，供应链获得的免费碳配额量也随之减少。由图8和表4的仿真结果表明，碳配额减少率越大，其免费碳配额量减少的速率越快，反映出碳交易量也随之增加，因此付出的碳成本也逐渐增加。对于企业来说，政府的碳排放量额度是有限，当碳配额量的减少时，为满足企业生产所需的碳排放量，企业会采取碳交易行为而获得更多的碳排放权，从而也付出一定的碳排放成本。

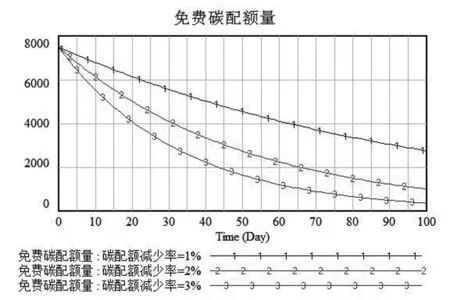
(a)

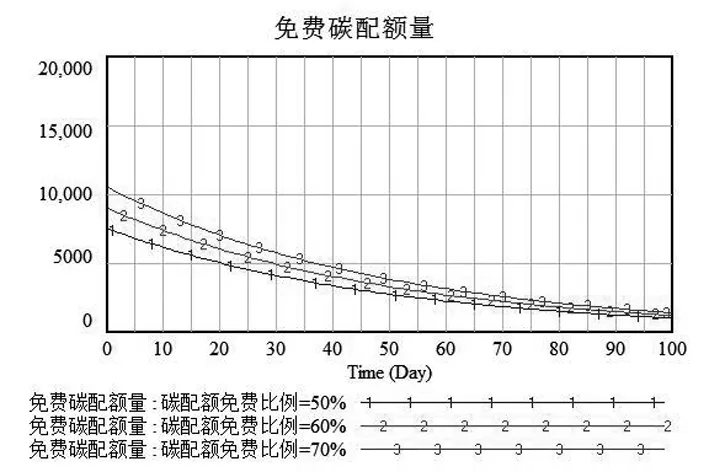
(b)

图8 碳交易政策下的仿真

2. 碳配额免费比例的模拟仿真分析

在其他参数不变的条件下，图8(b)模拟了不同碳配额免费比例下的免费碳配额量的变化过程。由图可看出，三条曲线的变化趋势几乎相同，随着时间推移呈现逐渐下降趋势。政府在节能减排方面为实现绿色供应链管理严格控制碳配额额度，因此无论碳配额免费比例多少，对于企业所分配的免费碳配额量来说都是呈逐渐减少趋势的。由表4的仿真结果表明，随着碳配额免费比例逐渐增大，企业在一定程度上会减少碳交易行为，从而承担的碳交易成本相应减少。

总之，政府在关注绿色低碳时要合理设置碳交易市场的碳配额额度和免费比例。若过度加大碳排放额度，虽然会使得整体供应链获得碳排放额度增大，企业减少碳交易行为，但企业在实现产能方面会投入更多的工作，产生的碳排放量会越多，对环境和碳市场会造成更大的压力。若碳排放额度过小，企业为实现产能需付出更多的碳排放成本，对企业经济造成一定压力。因此，政府需衡量经济和环境间的平衡点，合理分配碳配额额度与免费比例。

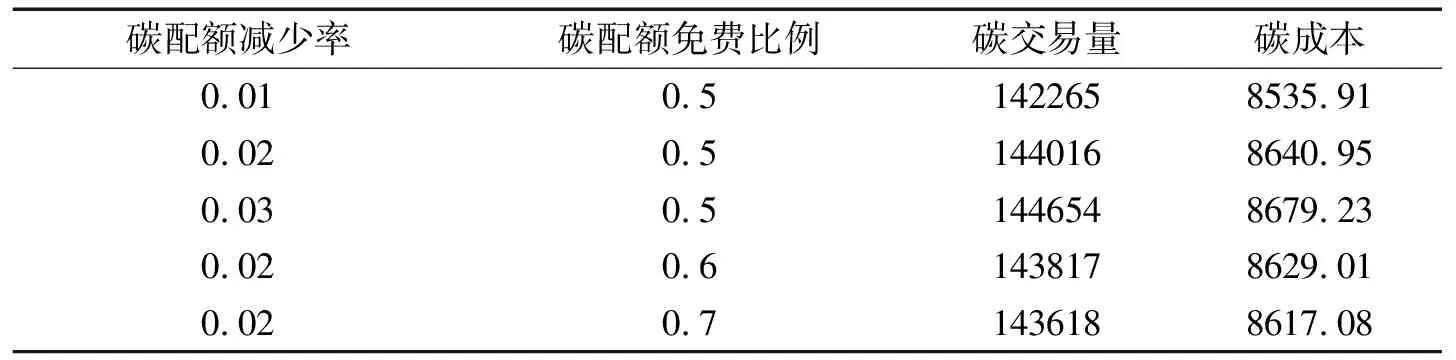
表4 碳配额减少率、免费配额比例对碳交易政策的影响

(二)碳奖惩机制

碳奖惩机制是指政府直接干预整个供应链生产运作过程中发生的碳排放量，对碳排放额度做出限制。当供应链企业的碳排放量超出限定排放额度时，政府会实施惩罚机制类似碳税一样征收税额，而当供应链的碳排放量低于规定额度时，采取相应的奖励。具体的系统动力学模型如图9所示。

模型中关于碳交易政策的新增的主要变量方程为：

碳奖励金额=IF THEN ELSE(碳配额与碳排放差额>0, 单位碳奖励*碳配额与碳排放差额, 0)；

碳惩罚金额=IF THEN ELSE(碳配额与碳排放差额<0, 单位碳惩罚*碳配额与碳排放差额, 0)

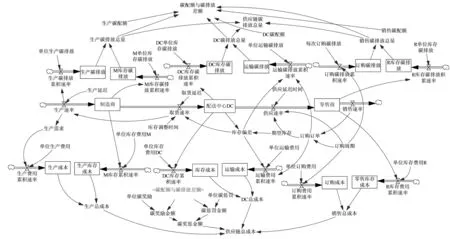
图9 碳奖惩政策下的系统动力模型

在其他参数不变的条件下，通过设定不同的碳配额总量和分配额度组合，探讨在不同订购周期下不同的碳配额额度对供应链决策的影响过程。由表5可知，随着周期增加，生产碳排放总量有小幅动波动，配送中心、销售商以及供应链碳排放总量则随着周期的增加而逐渐上升，而供应链总成本与周期则呈相反趋势发展。在此基础上，模拟不同的碳配额总量与碳配额分配组合，并通过这些组合判断供应链各个成员对给定配额的超额使用情况。其中，若超过碳分配额度用1表示，若未超过则用0表示。在决策周期时以未超过碳配额额度为主要依据，参考供应链总成本最小化原则决策，具体分析如表6所示。

表5 不同订货周期下的供应链碳排放与成本

表6 不同碳配额组合下订购周期决策

通过表6的比较分析可知，不同的碳配额总量通过不同的分配方式，供应链决策的订购周期有可能出现相同的情况，而相同的碳配额总量在不同的分配方式下也可能出现不同的决策周期。例如表6中1、2、4组，虽然碳配额总量不同，分配方式也不同，但它们的决策周期都为10天。而在2、3组中碳配额总量都为140000的情况下，通过不同的分配方式，其决策周期却不同。从图10中可观察到，随着碳配额总量的增加，供应链获得的碳奖励金额也越大或者惩罚金额也越少，其曲线呈波浪式下降趋势，具有一定周期性。在表6中，碳奖惩金额为负表示惩罚金额，为正则代表奖励金额，其金额数值与图中数值相对应。显然，若碳单位奖励金额越高，碳单位惩罚金额越低，供应链整体获得的碳奖励金额越大或惩罚金额也越小，反之碳单位奖励金额越小，碳单位惩罚金额越大，供应链整体获得的碳奖励金额越少或惩罚金额越大。

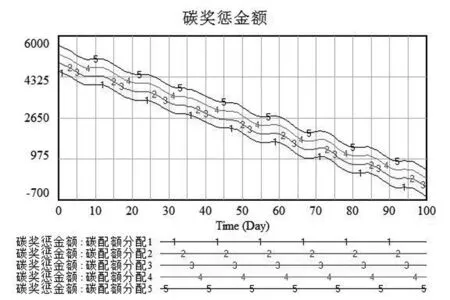
图10 不同碳分配方式下奖惩金额变化

在复杂的社会经济网络中，供应链是政策客体，政府为实施政策主体。当政府实施激励性政策措施时，会促使供应链企业进行主观意愿的碳减排。政府的规制性碳配额限制和碳配额分配会在一定程度促使供应链企业在环境效益和经济效益之间努力寻求平衡点，而相应的碳奖惩金额也会积极鼓励供应链企业采取低碳绿色技术生产低碳产品。因此，政府在实施碳奖惩机制时，需要根据现实制造业的实际碳排放情况与碳市场的碳额度，进行合理调控碳排放限额与分配组合。同时，碳奖惩机制政策的实施在一定程度能促使政府的目标通过传导机制在客体上实现，对环境效益和经济效益的期望目标起到权衡作用。

四、结语

本文以供应链碳排放系统作为研究对象，考虑了运作过程时滞效应对供应链碳排放量与成本投入变化的影响，利用系统动力学构建模型并进行瓶颈分析，探讨供应链运作中各项延迟时间对供应链最优决策选择的影响，并进一步分析了含运作时滞的供应链系统在不同碳政策影响下如何最优化碳排放与成本投入。研究结果表明，一方面，为有效减少供应链各成员的碳排放量和总成本，供应链生产运作过程中各项时间因素需合理控制，否则不仅达不到减排的目的，反而需投入更高的成本，影响减排效率。另一方面，在设立不同的政策情景下考察其减排效果时，发现碳市场对于供应链碳配额的分配方式十分重要。政府作为政策主体在实施碳税政策或奖惩政策时，应当综合考虑供应链的碳排放和总成本，兼顾环境效益与经济效益，在此基础上制定合理的碳排放限额、分配组合方式以及碳奖惩机制，引导供应链实施低碳化制造。本文仅考虑了供应链运作过程时滞问题，而对减排系统来说，还可进一步研究减排效果与碳政策实施的滞后效应问题以及供应链协调机制。

注释：

[1] Madani S. R.,Rasti-Barzoki M.,“Sustainable Supply Chain M anagement with Pricing,Greening and Governmental Tariffs Determining Strategies:A Game-theoretic Approach”,ComputersandIndustrialEngineering,vol.105(2017),pp.287-298.

[2] 赵道致、原白云、徐春秋：《低碳环境下供应链纵向减排合作的动态协调策略》，《管理工程学报》2016年第1期。

[3] 高举红、李梦梦、韩 冰：《考虑碳减排风险的闭环供应链网络设计》，《工业工程与管理》2017年第2期。

[4] 骆瑞玲、范体军、夏海洋：《碳排放交易政策下供应链碳减排技术投资的博弈分析》，《中国管理科学》2014年第11期。

[5] Ling Tang,Jiaqian Wu,Lean Yu,Qin Bao,“Carbon emissions trading scheme exploration in China: A multi-agent-based model”,EnergyPolicy,vol.81(2015),pp.152-169.

[6] 刘 婧、姚中杰、尹建中：《基于排放强度的产业间碳交易模型研究》，《东岳论丛》2015年第2期。

[7] Hua G.,Cheng T.C.E.,Wang S.,“Managing carbon footprints in inventory management”,InternationalJournalofProductionEconomics,vol.132,no.2(2011),pp.297-313.

[8] 唐建荣、郜旭东、张白羽：《基于系统动力学的碳排放强度控制研究》，《统计与决策》2012年第9期。

[9] Benjaafar S.,Li Yanzhi,Daskin M.,“Carbon footprint and the management of supply chains:Insights from simple models”,IEEETransactionsonAutomationScienceandEngineering,vol.10,no.1(2013),pp.99-116.

[10] Rui Zhao,Xiao Zhou,Jiaojie Han,Chengliang Liu,“For the sustainable performance of the carbon reduction labeling policies under an evolutionary game simulation”,TechnologicalForecasting&SocialChange,vol.112(2016), pp. 262-274.

[11] 周雄勇、许志端、郗永勤：《中国节能减排系统动力学模型及政策优化仿真》，《系统工程理论与实践》2018年第6期。

[12] 李 翀、刘思峰、方志耕、白 洋：《供应链网络系统的牛鞭效应时滞因素分析与库存控制策略研究》，《中国管理科学》2013年第2期。

[13] 石永强、彭 树、张智勇、杨 磊：《基于系统动力学第三方直通集配中心模式研究》，《管理科学学报》2015年第2期。

[14] 王伟钧、唐小我、倪得兵：《需求信息滞后下的零售商决策与牛鞭效应分析》，《中国管理科学》2008年第4期。

[15] 陈东彦、黄春丽：《滞后效应影响下低碳供应链减排投入与零售定价》，《控制与决策》2018年第9期。