基于模糊PID的双注浆泵同步系统的仿真与研究

王 婵，马月辉，于正航

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

0 引言

双注浆泵同步系统主要应用于高速铁路无砟轨道道床同步抬升控制系统，其中注浆泵为柱塞模式，以液压系统为动力源，液压缸活塞杆直接控制注浆泵活塞，从而控制进料与出料。为保证双注浆泵同步注浆，需要实现两个液压缸活塞杆以相同的位移或速度运动。理论上，要实现两液压缸同步运动，只需向两个结构参数完全相同的液压缸输入等量油液即可，但是由于一些不可避免的因素影响，例如:摩擦阻力、泄漏量、液压油中的杂质以及液压缸的制造误差等，都使得两液压缸的同步精度难以保证［1］。

于宗振［1］建立了双液压缸同步系统的数学模型，并进行了AMESim/Simulink联合仿真。但只应用了PID控制，没有涉及模糊控制;刘天豪等［2］分别利用Matlab/Simulink与AMESim软件对液压缸的同步控制问题进行了比较研究，但文中没有涉及控制算法，也没有进行联合仿真;孙静等［3］利用AMESim软件，分析了液压位置控制系统的动态误差与稳态误差。但仅是单个液压缸的输出位移跟踪给定信号，观察其同步误差。现针对双注浆泵同步控制系统，设计了模糊PID控制器，并对该系统进行了AMESim/Simulink联合仿真。与传统的未加控制算法的结果对比，加入模糊PID控制算法可以有效提高同步控制精度。

1 系统的组成及原理

系统的控制策略采用“主从方式”［4］，液压缸1作为主缸，其活塞杆位移跟随输入信号的变化而变化，将液压缸1的输出信号作为液压缸2的输入，使液压缸2跟随液压缸1位移的变化而变化，从而达到同步驱动的效果。控制策略框图如图1所示。

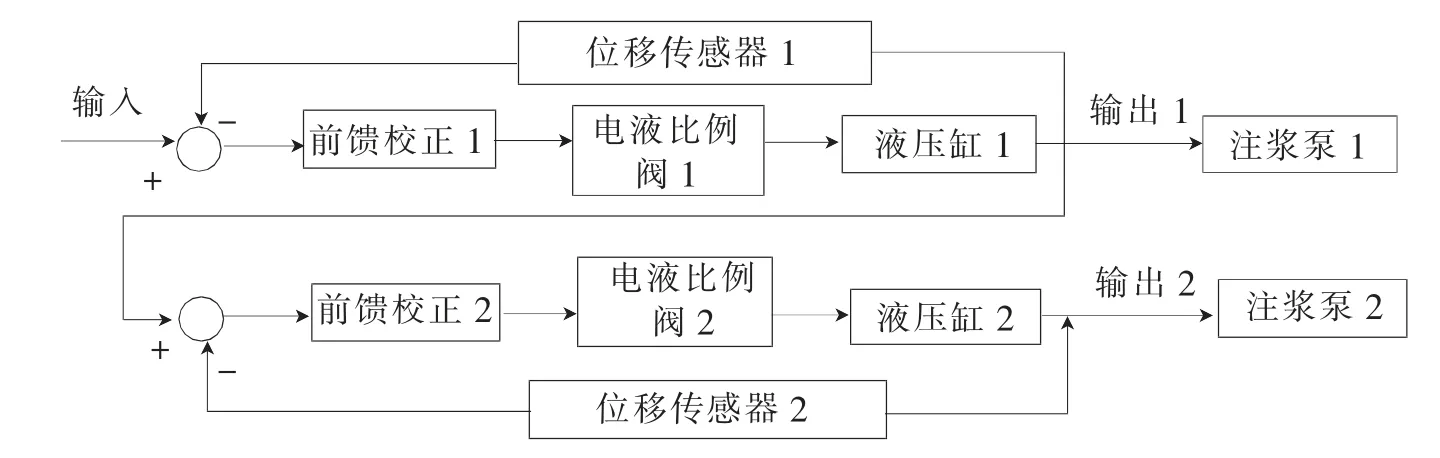
图1 “主从方式”控制策略框图

在该系统中，注浆泵是系统的关键设备，注浆泵的工作原理为:恒转速电机控制液压泵向液压缸供油，通过三位四通电磁换向阀左右侧电磁铁得失电来控制液压缸活塞杆的左右移动，液压缸活塞杆直接控制注浆泵活塞，从而控制进料与出料。注浆泵原理图如图2所示。

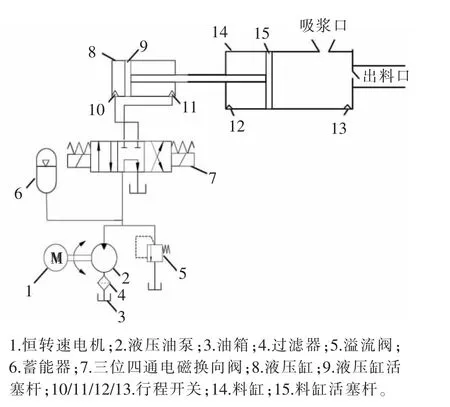
图2 注浆泵原理图

2 系统控制算法选择

由于双注浆泵同步系统具有不确定性以及非线性，因此常规PID控制无法达到预期效果，而单一模糊控制虽然可以实现非线性控制，也不需要被控对象的数学模型，但无法消除系统的稳态误差。因此，采用自适应模糊PID控制，使模糊控制与PID控制优缺点互补，从而使系统具有参数自整定、鲁棒性强、控制精度高等特点。

2．1 自适应模糊PID控制原理

自适应模糊PID控制将模糊控制与PID控制结合［5］，偏差e、偏差变化率ec和PID的3个参数Kp、Ki、Kd通过模糊推理建立函数关系，从而使这3个参数随e和ec的变化自动调整，其原理如图3所示。

2．2 自适应模糊PID控制器设计

在Matlab的fuzzy工具箱中建立模糊推理系统结构，输入为e、ec，输出为Kp、Ki、Kd。这5个变量的模糊集均为{NB，NM，NS，Z，PS，PM，PB}，论域均为［－3，3］，分别对输入和输出变量建立隶属度函数，其中PB、NB分别为S型和Z型隶属度函数，其它均为三角型隶属度函数［6］。其模糊规则如表1所示。解模糊方法选取重心法。

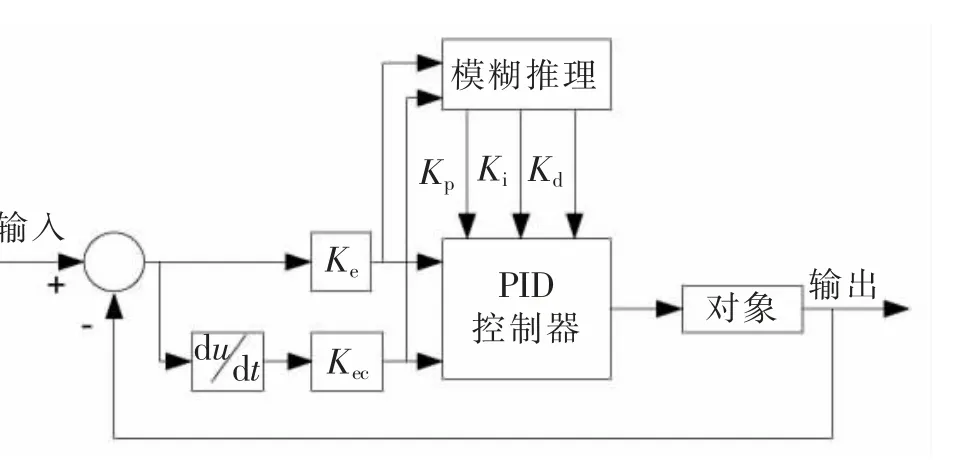
图3 自适应模糊PID控制原理图

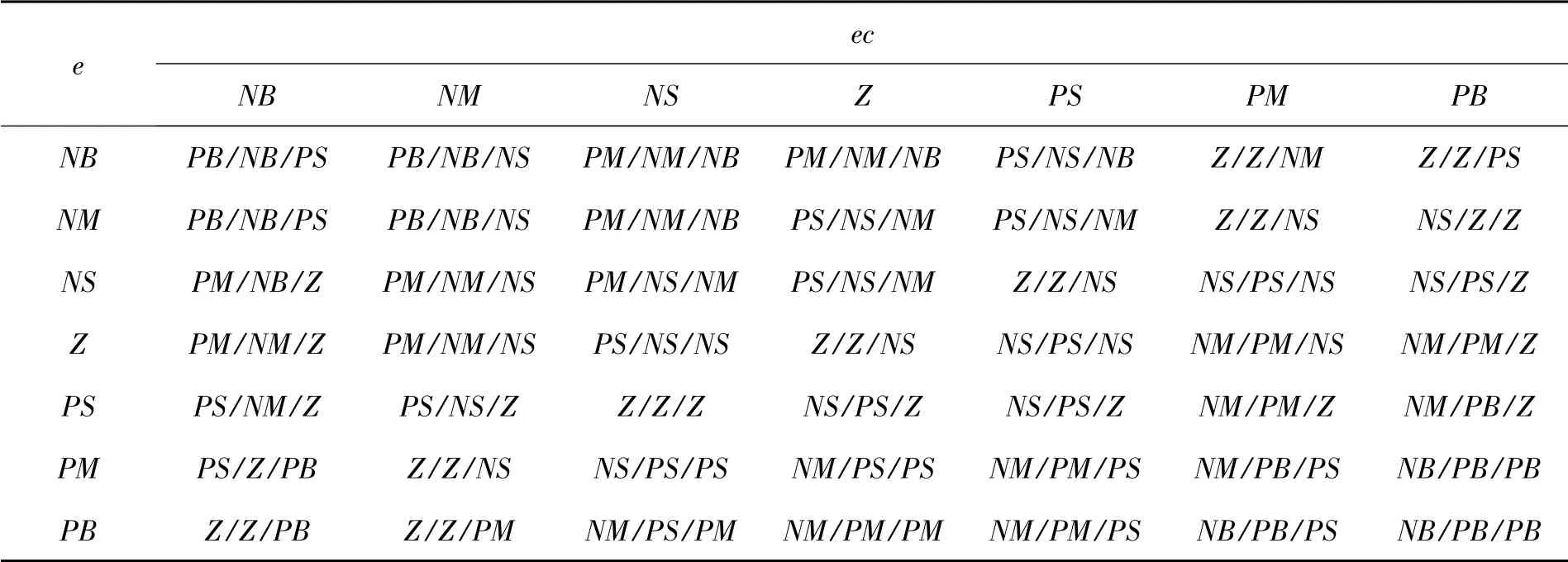
表1 模糊规则表

2．3 模糊PID控制系统的Simulink仿真

自适应模糊PID控制器在Simulink中的仿真模型如图4所示，图5为PID子系统结构图。

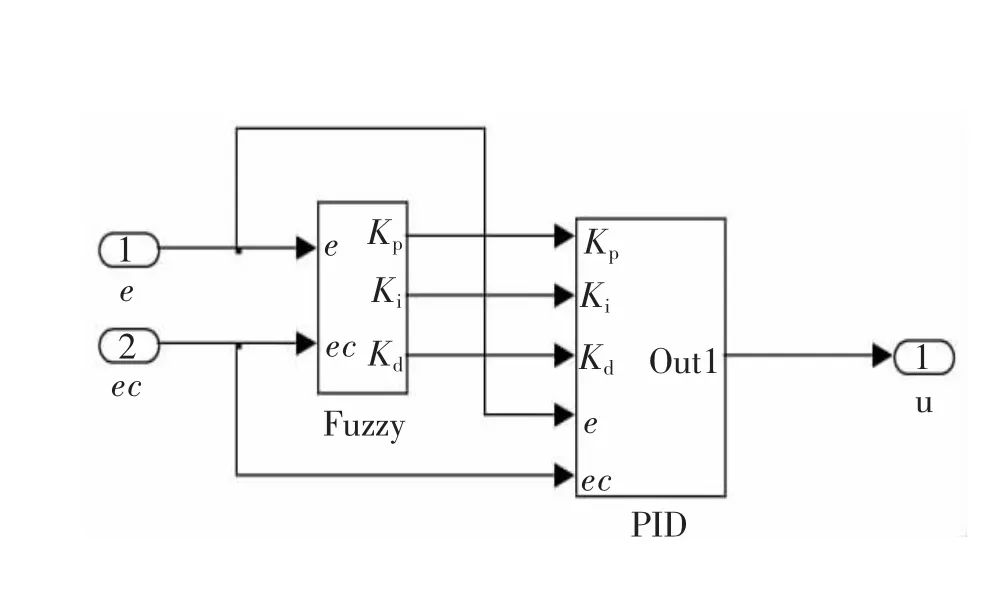
图4 自适应模糊PID仿真结构图

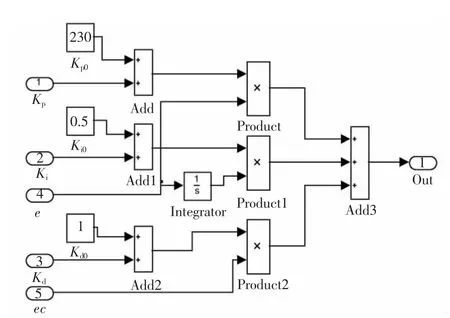
图5 PID子模型结构图

3系统AMESim仿真

3．1 未加控制算法的AMESim仿真

为验证两液压缸活塞杆位移是否同步，利用AMESim软件对同步系统进行仿真。仿真中，两个注浆设备的结构参数完全相同，参数设置如表2所示。

表2 仿真参数

对该系统进行AMESim仿真，未加任何控制算法时，两液压缸的位移曲线S如图6所示，同步误差曲线如图7所示。

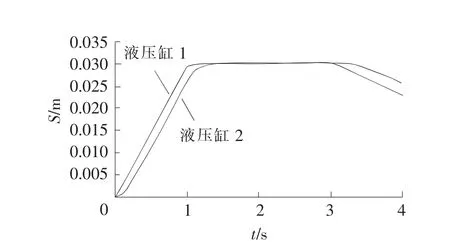
图6 位移曲线(K=500)

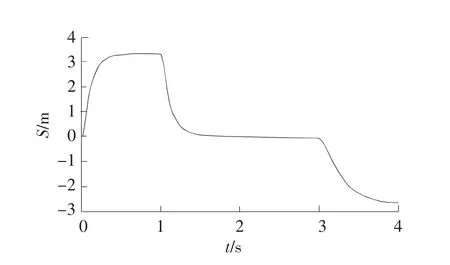
图7 同步误差曲线(K=500)

仿真中，由于液压缸2的输入信号为液压缸1的输出信号，因此，液压缸2对应电液比例阀的响应存在一定延迟，液压缸2的活塞杆运动滞后于液压缸1，从而产生误差。

由仿真曲线可以看出，液压缸2活塞杆位移能够跟随液压缸1活塞杆位移的变化而变化，但是跟踪精度不够高，同步误差较大，最大值达到了3．318 mm，不能满足要求的同步误差精度。

减小系统稳态误差的有效方法之一就是增大系统的开环增益K［7］，因此当系统的其它条件保持不变时，使得系统的开环增益K增大到600，位移曲线及同步误差曲线如图8、图9所示。

由仿真图可知，液压缸2的跟踪效果有所改善，系统同步误差峰值减小到2．071 mm，同步控制精度提高了1．247 mm。但是，由于高速铁路无砟轨道具有高平顺性，所以仅增大系统的开环增益K不能满足系统对同步精度的要求。

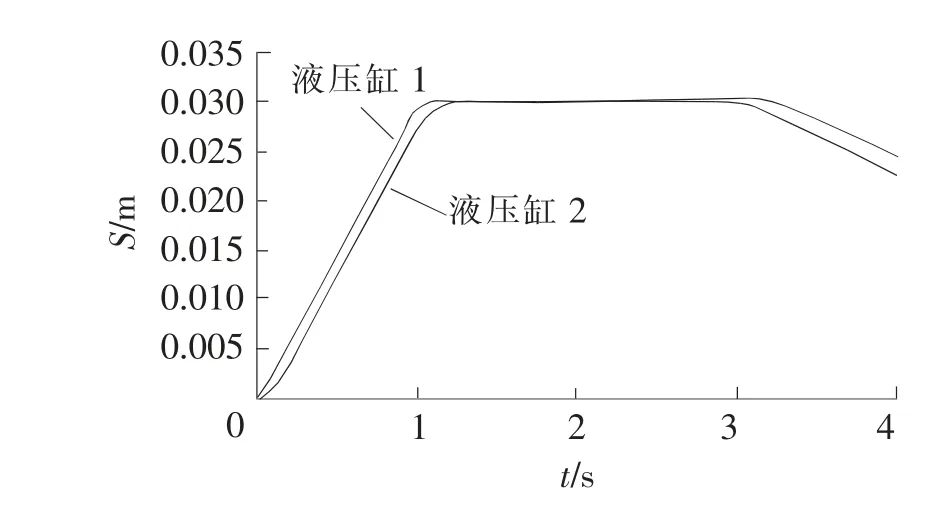
图8 位移曲线(K=600)

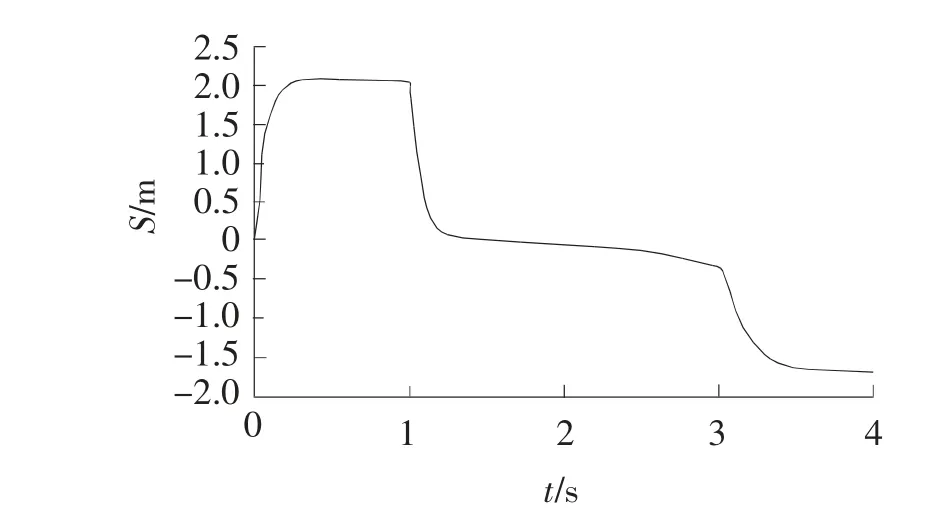
图9 同步误差曲线(K=600)

3．2 加入模糊PID后的AMESim/Simulink联合仿真

AMESim为用户提供一个图形化的建模仿真平台，用于工程系统建模、仿真以及系统的稳态和动态性能分析［4］。通过模型库搭建设计模型，并设定模型的参数结构，即可对系统进行稳态及动态仿真，并根据仿真曲线分析结果。但是在AMESim中建立数学模型是有难度的，此时需要Matlab/Simulink软件辅助完成系统仿真。在AMESim中对系统建模，并以S函数的形式导入到Simulink的数学模型中，从而实现联合仿真，这样可以大大减少建模的工作量。因此在系统中加入模糊PID控制器时利用AMESim/Matlab进行联合仿真会更加简便。同步注浆系统联合仿真模型图只需在未加任何算法模型的基础上加上联合仿真模块即可，联合仿真模型如图10、图11所示。

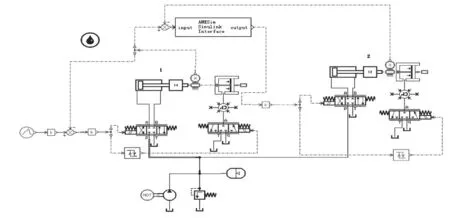
图10 同步注浆系统AMESim/Simulink联合仿真模型图

仿真结果如图12、图13所示。

由仿真图可知，给定信号不变，加入模糊PID控制算法后，液压缸2的跟踪情况发生了变化，液压缸2的位移能够准确地根据液压缸1的位移变化而变化，实现了有效跟踪。

胡爱闽［8］采用主从控制方式实现液压升降台同步控制，同步误差最大值为0．023 mm。鲁鼎［4］采用试凑法对PID参数整定，同步误差最大值为0．018 mm。由图13可知，该系统两液压缸活塞杆位移差在0．8 s处达到最大，最大值约为0．014 mm。仿真结果表明，自适应模糊PID控制可以实现PID的参数自整定，提高系统的灵活性和稳定性，并有效提高系统的同步精度。

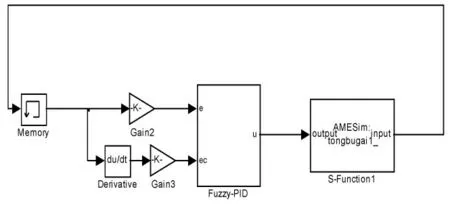
图11 同步注浆系统Simulink模型图

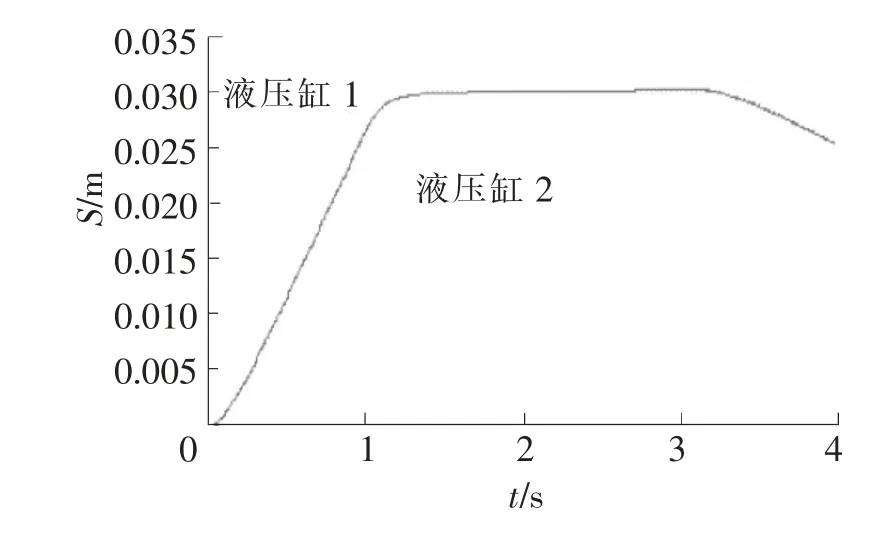
图12 加模糊PID后位移曲线

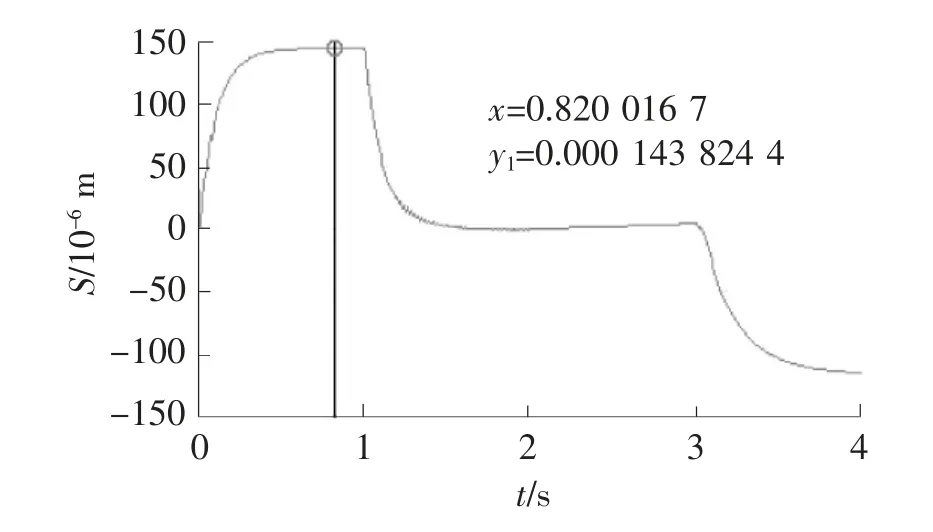
图13 加模糊PID后同步误差曲线

4 实验验证

模拟实验采用博世力士乐旗下WS290试验台，该设备主要应用于液压控制系统。位移传感器采用KPM22-225 mm。根据AMESim仿真模型，利用该设备搭建双注浆泵同步系统，验证两液压缸活塞位移是否同步。表3为未加入模糊PID的实验结果，表4为加入模糊PID后的实验结果。

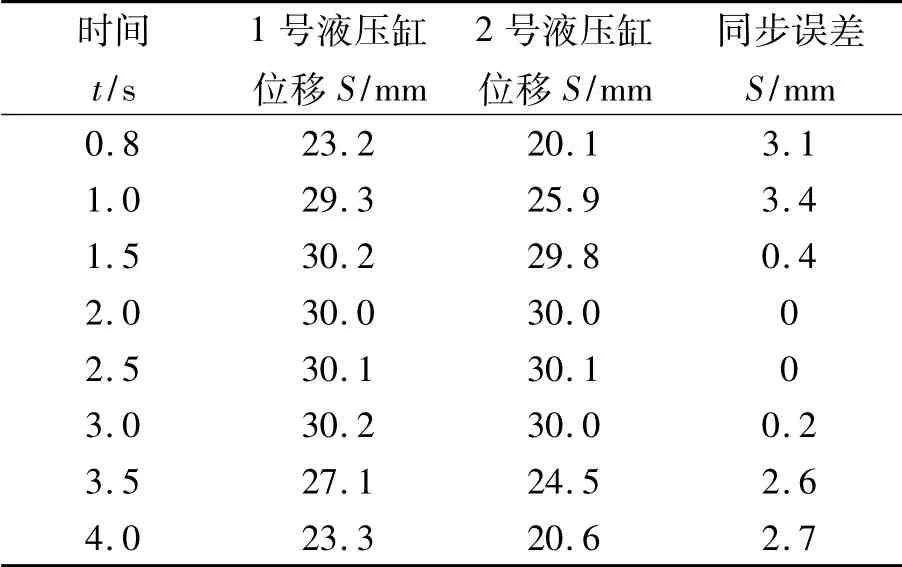
表3 未加模糊PID实验结果

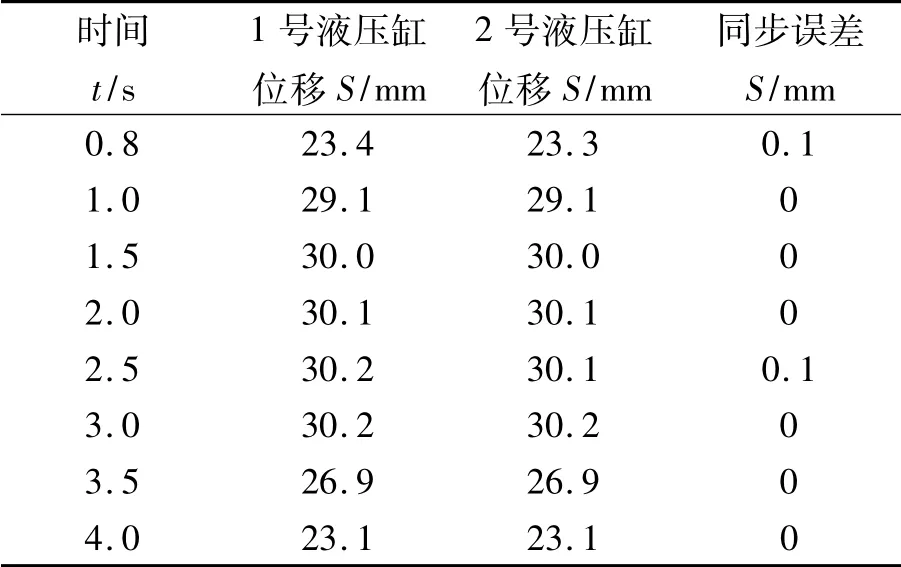
表4 加入模糊PID后实验结果

由表3可知，未加模糊PID控制的同步误差最大值达到3．4 mm。由表4可知，加入模糊PID控制后液压缸1与液压缸2的活塞杆位移基本保持一致。在模拟实验中，由于环境与设备安装误差等因素的影响，模拟实验控制精度与软件仿真存在一定偏差。本实验验证了模糊PID控制的有效性。

5 结论

(1)针对双注浆泵同步系统，设计了自适应模糊PID控制器，使PID的3个参数能够在线自整定，大大提高系统的工作效率，另外，通过AMESim与Simulink软件对该系统的联合仿真，验证了自适应模糊PID控制可以提高系统的灵活性和稳定性，并使系统的同步误差控制在±0．02 mm范围内，与未加入模糊PID控制算法的同一系统相比，同步精度有了明显提高。

(2)针对提出的方法，对该系统进行了模拟实验，加入模糊PID控制的两液压缸活塞杆位移基本保持一致。实验结果验证了该方法的有效性。

(3)该同步注浆系统为高速铁路无砟轨道道床同步抬升控制奠定基础，此后将继续研究双注浆泵的流量跟踪问题，使得双注浆泵同步控制系统的同步效果更好。