基于Lorenz混沌同步系统的未知频率微弱信号检测

李国正， 谭南林， 苏树强， 张 驰

(北京交通大学 机械与电子控制工程学院, 北京 100044)

微弱信号是指深埋在背景噪声中的极其微弱的有用信号，如弱光、微温差、微振动、弱磁、微电流等。检测微弱信号在航空航天[1]、故障诊断[2]、生物医学[3]、通信传输[4]、系统辨识[5]等领域有着及其广泛的应用。随着科学技术的发展，对微弱信号的检测，越来越受到重视，需求量日益增加。该项技术的进步对相关行业的发展会产生深远影响，具有重要意义。将淹没在强噪声背景下的微弱信号快速、准确的检测出来是信号处理领域的热点问题，受到国内外学者的广泛关注。

传统微弱信号检测方法多基于线性系统，这使得有用信号被放大的同时，背景噪声也随之放大，而采用滤波器滤去噪声的同时，信号会有所损失。混沌类微弱信号检测方法基于非线性系统，充分利用了混沌系统具有的初值敏感性、噪声免疫性和非线性放大特性来实现信号检测，可以检出信噪比低至的微弱信号。此类方法自20世纪90年代提出后，很多学者对此展开了深入的研究[6]，该方向成为了混沌理论应用于实际工程的研究热点之一。

现阶段的研究主要集中在以下四个方面：一是对混沌系统检测机理的分析和探讨。代表性的研究有：王永生等[7]研究了数值解算时计算步长和驱动输入白噪声对弱信号检测中Duffing振子运动特征的影响。吴彦华等[8]研究了待检信号与Duffing系统内置信号频差和相差对系统相图的影响，提出了微弱信号盲检测识别算法，建立了检测模型。孙文军等[9]研究了Van der Pol振子相态跃迁模型，从理论上证明了其用于弱信号检测的可行性，并与Duffing振子进行了对比分析。二是对混沌系统相空间运行轨迹计算和运行状态判定方法的研究。其中，Rashtchi等[10]提出通过计算相空间轨迹自相关系数判断状态转变的方法，并与最大Lyapunov指数法进行了比较。Awrejcewicz等[11]利用Melnikov法预测了非线性系统振子在微作用力下系统自由度的改变，并通过数值仿真证明了该结论；三是对构建检测系统应用于工程实际方面的研究。其中，温宇立通过数值模拟和实验研究,验证了Duffing混沌系统的相轨迹识别多裂纹管道超声导波信号的有效性。Zhao等[12]结合混沌和倒谱分析的方法对液压试验机梭阀的早期故障进行诊断。张伟伟等[13]提出一种基于改进型Duffing混沌振子系统的强噪声下超声导波的识别和定位方法，并利用导波信号对系统相轨图的显著变化识别导波信号。陈志光等[14]研究了强海洋背景噪声下微弱周期信号的检测，提出利用希尔伯特变换实现对间歇混沌的包络检测的新方法。四是对频率未知微弱信号检测方法的研究。其中，李国正等[15]提出了构建Duffing振子阵列，结合遗传算法寻找输入信号后相空间方差最大值所对应的频率量，以实现频率估计的方法，以及基于蔡氏电路构建的混沌同步系统进行待测信号参数估计的方法[16]。孙自强等[17]采用取样积分技术提高混沌振子对增速箱振动故障信号的检测门限,利用混沌振子相图变化实现齿轮早期故障诊断。

上述研究表明，利用混沌系统的相关特性进行微弱信号检测可以极大消除背景噪声的影响，进而提升被测信号的信噪比，降低检测门限，是很有潜力的微弱信号处理技术。但上述方法受参数设定、相空间轨迹求解、运行状态判定等因素的影响，仍存在检测效率偏低、状态转换易误判等不足。尤其对未知频率的周期信号进行检测时，基于间歇混沌现象或基于优化算法的检测方法所采用的混沌系统阵列结构非常复杂，需要在整个频域区间内扫描估计，且难以处理含有多个周期信号的被测对象，这大大影响了它的适用性。

为此，本文首先从典型Lorenz系统的信号检测机理展开研究，采用驱动-响应法构建基于混沌同步方式的微弱信号频率检测系统。再结合MUSIC(Multiple Signal Classification)算法处理降噪后得到的同步误差，实现频率估计。最后，采用建立的模型进行对比试验，验证其可行性。新方法综合利用了混沌系统的初值敏感性、抗噪性、非线性放大性和同步性，从而简化系统参数设定，避免相空间轨迹复杂求解，提高了检测效率。

1 系统模型与频率估计

1.1 频率检测系统模型和工作机理

本文提出的新方法所检测的对象是强噪声背景下微弱周期信号的频率值，其表达式为：

r(t)=s(t)+n(t)

(1)

式中，s(t)是微弱正弦信号Asin (ωt+θ)，n(t)是白噪声信号N(0,σ2)。该信号信噪比小于-20 dB，对频率值ω进行估计。

考虑到现有混沌类检测方法基于单一混沌系统进行检测时仍未解决的诸多难点问题，本文提出引入一个新的具有相同结构和参数的混沌系统，利用两个混沌系统之间可以同步运行这一特性，结合MUSIC算法，来实现微弱信号的频率检测。该频率检测系统的原理性框图，如图1所示。

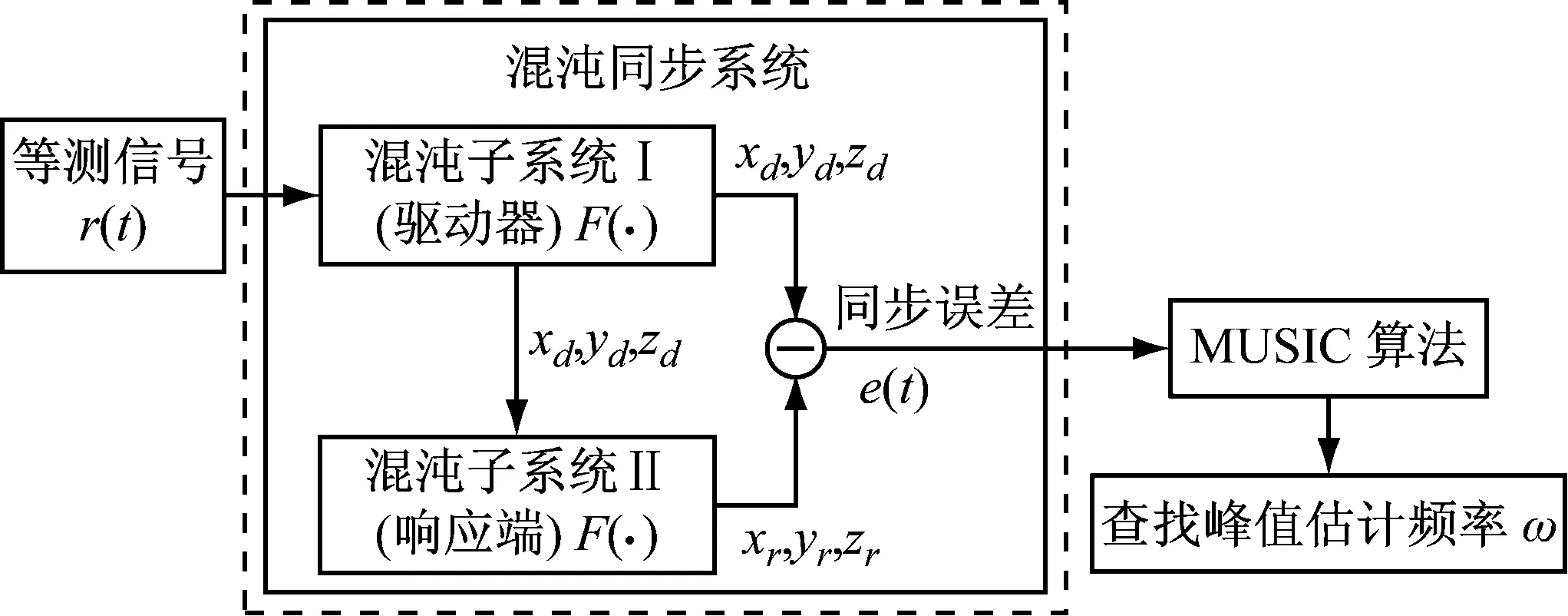
图1 混沌同步频率检测系统原理图

图1中，混沌子系统I作为同步系统的驱动端，混沌子系统II作为响应端，二者之间采用驱动-响应法实现同步。当待测信号接入驱动端后，引发其相空间运行轨迹发生了巨大改变。受混沌系统的初值敏感性和噪声免疫性的影响，驱动端放大周期信号的同时，对背景噪声产生抑制作用。而响应端的相空间轨迹作为对比，可得到同步误差e(t)，以此评估输入信号后相空间轨迹产生的变化。MUSIC算法作为空间谱估计测向理论的重要算法，进一步消除噪声所产生的影响。用其处理同步误差，查找空间谱峰值，最终实现频率估计。

1.2 Lorenz系统及参数设定

现有混沌类检测方法大多基于单个Duffing振子搭建系统。该系统内包含一个周期策动力。测量不同频率的周期信号时，需要对其策动力参数进行调整，或是采用阵列结构覆盖整个需要检测的频率区间，这大大增加了构建难度。Lorenz系统由麻省理工大学教授Lorenz首次提出，是一个常微分方程组，在某些参数值和初始条件有混沌解[18]。其数学模型如下

(2)

式中，r(t)是接入的被测信号，它在典型的Lorenz系统中并不存在，此时系统转换成为一个更高维的非线性动力学系统。对该模型的动力学特性进行研究，取结构参数为：σ=10,β=2.6。改变参数ρ的取值，得到系统的分岔图，如图2所示。

图2 参数ρ的分岔图

图2中，参数ρ的取值范围为[0,250]。随着参数值增加，系统的运行状态在多周期态和混沌态之间变换。状态转化的临界点有24、98、150、169、215，可以据此划分成6个子区间。其中，区间I、IV和VI内，系统运行在多周期态；区间II内，运行在混沌态；区间III内，主要为混沌态，特定数值出现多周期态。进一步分析系统处于不同状态时，输入信号对相空间运行轨迹的影响。取ρ=169和ρ=50，并输入不同类型的待测信号，得到的相空间轨迹如图3所示。

图3的相空间轨迹包含有四条曲线，曲线a是输入信号r(t)=0时得到，曲线b是r(t)=0.001sin(t)时得到，曲线c是r(t)为方差等于0.001白噪声时得到，曲线d是由曲线b中的正弦信号叠加曲线c中的白噪声信号得到。图3(a)中，系统运行在三周期态，四条曲线的运行轨迹在相空间内几乎完全重合，难以区分，无法应用于信号检测。图3(b)中，系统运行在混沌态时可以看出，在非线性系统的作用下，曲线a和曲线c非常接近，而曲线b和曲线d也保持基本一致，而曲线a和c与曲线b和d相比，系统的运行轨迹则发生了巨大的偏移。

为了进一步分析不同参数条件下输入信号对相空间运行轨迹产生的影响，逐步增加Lorenz系统的参数ρ，同时获取上述四种信号输入时系统的运行轨迹。以此计算正弦信号输入、白噪声输入、正弦信号叠加白噪声输入时空间轨迹相对于无测试信号输入时运行轨迹的偏移量，绘制其与参数值ρ之间的关系曲线，分别对应于曲线a、b和c，如图4所示。

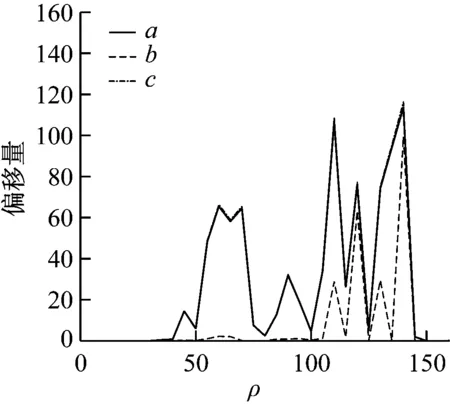
图4 参数ρ与轨迹偏移量之间的关系曲线

结合图4、与参数ρ的分岔图可以看出，不同信号输入时，轨迹偏移量的大小除了与信号种类相关外，还与ρ的取值使系统所处的运行状态有关。当ρ的取值在图2中对应的区间I和IV内时，系统运行在多周期态，三种输入信号对应的偏移量小；取值在区间III内时，系统在混沌态和多周期态之间切换，三种输入信号对应的偏移量波动剧烈；取值在区间II内时，系统运行在混沌态，输入信号中的白噪声使系统的相空间轨迹在原有运行轨迹的周围发生小幅抖动，而周期信号则使得空间轨迹产生了很大的偏移，且该偏移量远大于输入信号的幅值。当参数ρ在此区间内时，适用于信号检测中的降噪处理。如果能够获取输入信号前后相空间轨迹发生的变化，则可以从其偏移量对相关参数进行估计。

1.3 Lorenz混沌同步系统

参照图1的系统框架，基于Lorenz系统，采用驱动-响应法构建同步系统。驱动端混沌子系统I的状态方程是

(3)

响应端混沌子系统II的状态方程是

(4)

可以证明，当混沌系统中的参数满足条件σ>0和β>0，且输入信号r(t)=0，子系统I和II可以实现同步。

为了证明上述结论，构建Lyapunov函数如下式

(5)

对其求导可以得到

(6)

结合假定条件r(t)=0，并用式(3)减去式(4)，可以得到下式

(7)

代入式(6)，可以得到

(8)

显然，结构参数σ>0,β>0，时，上式小于0。根据Lyapunov稳定性定理可知所建立的系统的同步误差在零点位置渐进稳定，上文子系统I和II同步的相关结论成立[19]。

1.4 MUSIC算法与频率估计

当输入信号r(t)作为扰动项接入所建立的同步系统后，会出现同步误差。根据上文分析可知，同步误差主要受到输入信号中周期信号成分的影响而产生，由此推断同步误差的信噪比与被测信号相比会有极大改善。MUSIC算法是Schmidt提出的一种基于矩阵特征空间分解的方法[20]，是空间谱估计测向理论的重要基石。很多学者对该算法的效率、敏感度等方面展开了研究和分析，结果表明该算法可以有效减少噪声的影响，准确估计信号频率。我们采用该算法对同步误差进行处理，基本流程如下：

步骤1将同步误差e(t)作为变量X，取延时变量为T，获取新的同步误差序列e(t+T)作为变量Y。变量X和Y包含有L个数据。

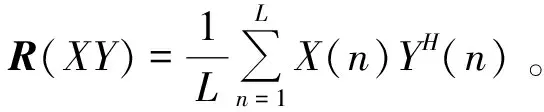
步骤3对矩阵R(XY)进行特征分解，得到其特征值λ1,λ2,…,λM以及特征向量υ1,υ2,…,υM。将特征值由大到小排列，取前d个对应的特征向量，构建信号特征矩阵US=[υ1,υ2,…,υd]。剩下的特征向量构建噪声特征矩阵UN=[υd+1,υd+2,…,υM]。

步骤5查找空间谱的峰值，其对应的频率值即为被测信号频率的估计值。

为了检验该方法的有效性，进行了两组试验。取Lorenz系统参数为σ=10,β=2.6和ρ=50，此时系统处于混沌态。将正弦信号0.001sin(2πt)与白噪声(N(0,0.05))叠加，作为输入信号接入该系统，其信噪比为

SNRr(t)=10lgPs(t)/Pn(t))=-50 dB

(9)

再将正弦信号的频率变为50 Hz，保持信噪比不变并接入该系统。两次同步误差计算得到的空间谱，如图5所示。

由图5可知，淹没在强噪声背景中的正弦信号的频率值可以从同步误差的空间谱中准确得到。图中的多条曲线是以被测信号的周期长度为基本单位，取其1倍～10倍长度的同步误差数据，用MUSIC算法计算得到。可以看出随着数据长度的增加，频率估计值不断逼近实际值。当长度为被测信号周期长度的4倍时，得到的频率值分别为0.99 Hz和49 Hz，与实际值基本一致。

2 系统检测特性分析

2.1 幅值与频率的检测范围

接入的被测信号使Lorenz系统的相空间轨迹出现扰动，进而对其运行状态产生影响。为此，需要对被测信号幅值与频率的有效检测区间进行分析。我们采用维持Lorenz系统的结构参数不变，获取输入信号幅值A的分岔图，以及维持被测信号信噪比不变，获取同步误差信噪比的变化曲线的方法分别进行研究。结果如图6所示。

图6(a)可以看出，引入的待测信号改变了Lorenz系统的原有动力学特性。当幅值为45、104和167时，系统处于状态转化的临界点。根据前文的分析可知，频率检测要求系统运行在混沌态。通常来说被测微弱信号的幅值较小，大多处于0

2.2 方法对比

基于Lorenz混沌同步系统的未知频率检测方法与现有的混沌类检测方法在检测原理和实现方法上并不相同。分析新方法与现有混沌类检测方法在构建模型、测量范围、检测参数、检测效率四个方面的区别，其结果如表1所示。

其中，方法1是基于单一Duffing振子，检测被测信号的幅值；方法2和3采用多个Duffing振子组成阵列，分别基于间歇混沌现象和优化算法匹配被测信号的频率；方法4基于Chua电路和自适应控制算法检测信号的频率；新方法基于Lorenz系统和MUSIC算法获取信号频率。

根据上述方法的检测机理可知，方法1,2,3是需要将系统设定在Duffing振子状态转换的临界点，并通过状态转换情况进行判定。若输入信号叠加Duffing振子系统内原有策动力后所产生信号的幅值超过系统状态转换的下一临界点，将无法引发系统运行状态改变，从而引发误判。因此，输入信号的幅值大小不能超过两个临界点之间的区间长度。当使用方法1,2,3中Duffing振子的结构参数时，输入信号的有效幅值输入区间为[0,0.5]。方法4基于Chua电路，进行检测时要求信后输入前后系统能稳定运行在混沌态，避免进入周期态和发散态。当Chua电路采用方法4中结构参数时，输入信号的有效幅值区间为[0,0.014]。根据上文的研究可知，新方法基于Lorenz系统构建，输入信号的幅值在区间[0,45]内时，均可以实现信号检测。因此，对比上述方法的可测量幅值区间可以得出：S≫S1=S2=S3≫S4。

方法1无法测量信号的频率值，方法2和方法3的频率检测范围理论上可以通过增加振子个数或动态调整策动力参数的方式来满足任意频率区间的检测需求。但增加振子个数会使系统结构更加复杂，大大增加系统成本。在相同构建成本的约束条件下有：F≈F4≫F3≈F2≫F1。

方法2需要按照扫频方式逐步匹配的频率值，方法3则需要不断迭代求解信号频率，这都会大大增加检测时间，进而影响检测效率。根据相关实验有：T≈T4≪T1≪T3≪T2。

由此可见，基于Lorenz系统构建的混沌同步系统与现有混沌类检测方法相比，在有效幅值、频率检测区间和检测效率上均具有优势。

3 实验验证

为了对上述方法的有效性进一步进行检验，采用电容、电阻、运算放大器(LM741)和模拟乘法器(AD633)，搭建实际Lorenz系统混沌同步检测电路，如图7所示。

图中左侧电路为同步电路的驱动端，右侧电路为响应端。运算放大器和模拟乘法器的供电电压分别为±18 V和±10 V。列出驱动端电路的状态方程有

(10)

式中，A，B，C处的电压值VA，VB，VC与Lorenz系统的状态变量xd，yd，zd相对应。r(t)为输入的被测信号，由正弦信号和白噪声叠加而成。参照上文仿真的Lorenz系统参数值，C1=C2=C3=0.1 μf，R1，R2，R3，R4，R6，R7，R8，R10，R11，R12，R14为10 kΩ，R5=2 kΩ，R9=100 kΩ，R13=38 kΩ。而响应端电路的状态方程与上式类似，所用元件的参数值与驱动端同一位置处的元件保持一致。此时同步电路的状态方程与上文Lorenz同步系统的状态方程(3)和(4)完全一致。

图7 Lorenz系统混沌同步检测电路图

采用信号发生器叠加幅值为0.001，频率为30 Hz的正弦信号和白噪声接入该电路，同时记录上述各点处的电压值，采样率取100 kHz，记录时长为0.2 s。绘制系统的相空间轨迹图和同步误差空间谱，如图8所示。

上图可见，所设计的Lorenz同步检测电路运行在混沌态，计算接入被测信号后同步误差的空间谱，通过峰值可以观察到此时被测信号的频率值为30 Hz，与实际输入的被测信号完全一致。

4 结 论

本文提出了一种基于混沌同步系统测量强噪声背景下微弱信号频率值的新方法，采用Lorenz系统构建了相应的检测模型，研究了系统的检测机理、参数设定准则和有效检测范围，对比分析了新方法与现有混沌类检测方法在模型结构、可测量参数和检测效率等方面的区别，并搭建检测电路进行了实验验证。新方法利用了混沌系统的可同步性，采用MUSIC算法直接从同步误差获取待测信号的频率值，在保留混沌系统优良检测特性的同时，解决了现有方法参数设定复杂和系统运行状态判定困难的问题，大大提升了检测效率和适用性，有利于应用于实际工程，还可与传统时频域信号处理方法进行结合，形成新的微弱信号检测方法，为检测低信噪比条件下的微弱信号提供新的途径。