翻转动能对基础隔震剪力墙结构高宽比限值的影响分析

赖正聪， 潘 文， 白 羽， 叶燎原

(1. 昆明理工大学，建筑工程学院， 昆明 650500；2. 云南省抗震工程技术研究中心， 昆明 650500； 3. 云南师范大学， 昆明 650500)

基础隔震技术通过在建筑底部与基础之间曾设柔软隔震层，延长结构周期、降低地震力、减小结构地震反应。文献[1-3]根据历次震害调查结果指出，隔震结构地震反应可降低至非隔震结构的1/8～1/2,遭受设防烈度及其以上强度地震后，非隔震结构多数进入塑性甚至破坏、倒塌，而隔震结构基本保持弹性。相比较非隔震结构而言，基础隔震结构在抵抗可能遭遇的超罕遇烈度地震作用方面，具有更高的安全储备，优势更为显著。目前在世界范围内对隔震技术的研究、应用正逐渐由多层建筑向高宽比较大的高层建筑延伸。相对于已普遍应用的多层隔震技术，高层建筑隔震尚需针对抗地震倾覆等问题作进一步探索及研究。

文献[4]基于反应谱理论给出结构平动方向上的动力加速度响应及由此引起的水平地震作用倾覆力矩，通过倾覆翻转静态力矩平衡计算隔震层翻转角，给出了不考虑转动惯性力所引起的动力效应情况下的基础隔震结构对应不同阻尼比及场地条件的高宽比限值。

文献[5]对高宽比分别为2.5和5的两个隔震结构进行了地震模拟振动台对比试验研究，发现大高宽比结构较小高宽比结构的倾角反应更为剧烈，意味着上部结构将发生翻转运动，并具有相应转动动能。文献[6]对简化的隔震结构三质点模型进行分析，得出高阶振型影响可不考虑的结论。文献[7]则通过建立高层框剪隔震结构有限元模型，对高层隔震结构减震机理进行探讨，并得出隔震后高阶振型将显著衰减的结论。

剪力墙结构作为我国高层建筑广泛采用的结构型式，其自身抗侧移刚度较大，相对侧移变形较小。基础隔震剪力墙结构在地震作用下，上部结构水平向将呈现出近似整体刚性平移、翻转的动力响应特征[8]。在对其进行动力响应分析时，考虑隔震层翻转角影响的情况下，在单一方向上取前两阶振型计算所得振型参与质量系数便可达95%以上[9]。

本文针对抗侧刚度相对较大、质量沿高度分布相对均匀的基础隔震剪力墙结构，建立了同时考虑平动及翻转动能的两自由度简化分析模型。并结合我国加速度反应谱，以隔震支座不受拉为倾覆控制条件，阐述了考虑转动动能影响的高宽比限值动力分析方法。通过与静力法作比较，揭示翻转动能对基础隔震剪力墙结构高宽比限值的影响。

1 静力倾覆分析

首先，针对图1所示的基础隔震高层剪力墙结构作如下基本假定：① 上部结构质量及抗侧移刚度沿高度分布较为均匀，所受到的水平地震力近似呈矩形分布；② 隔震层顶部梁板刚度较大，忽略弹性变形影响；③ 隔震层同规格支座对称布置；④ 以隔震支座不受拉为倾覆控制条件。

上部结构在水平地震力(仅考虑单一水平方向)作用下，对隔震层产生的倾覆力矩MEh将使隔震层产生翻转角θ，若将其简化为单自由度模型，仅考虑水平向的振动，则隔震层边缘支座由此引起的最大轴向力NBEh为

(1)

式中：B为隔震层宽度，KVB为边缘隔震支座竖向刚度，Kθ为隔震层整体等效抗翻转刚度。

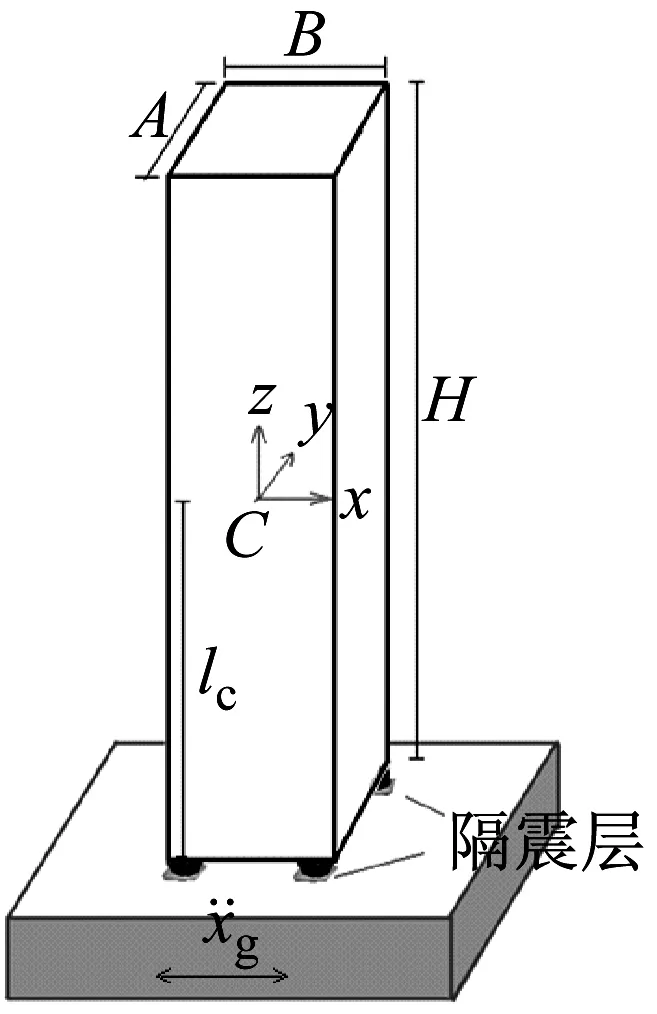
图1 基础隔震高层剪力墙结构简化分析模型

根据基本假定，倾覆力矩MEh可按下式计算

MEh=FEKlc

(2)

式中：lc为隔震层距离上部结构质心的高度，FEK为上部结构所受到的最大水平地震作用标准值，且有

(3)

将式(2)、(3)代入式(1)可得

(4)

显然，以上分析实质上仅考虑了水平向的动力过程，而将倾覆翻转方向视为静力过程，通过静态力矩平衡计算翻转角，不考虑转动惯性力的影响。本文将该方法称为等效静力倾覆分析法。对于刚度较大的剪力墙结构，随着高宽比的增大，由其整体翻转运动所产生的转动动能趋于显著，其影响需作进一步的研究。

2 考虑翻转动能影响的动力倾覆分析

2.1 动力微分方程

假设上部结构质量为m，总高度为H，分析方向上结构宽度为B，整体绕质心C的等效转动惯量为Jc，隔震层整体水平等效刚度为Kh，阻尼系数为Ch。由隔震支座竖向阻尼产生的隔震层整体等效翻转阻尼系数为Cθ，Kθ意义同上。

以上部结构质心C为原点建立坐标系，以质心水平位移xc和结构转角θ为广义坐标，则系统总动能T包含整体平动及翻转动能两部分，可表达为

(5)

系统势能为

(6)

将式(5)、(6)代入Lagrange方程，得到振动微分方程

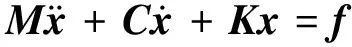
(7)

其中

将式(7)展开便得

(8)

式(8)第1式等号两边同乘lc，移项整理后得

(9)

代入式(8)第2式整理后得到转动动力方程

(10)

由式(10)可见，等效静力倾覆分析方法实质上仅考虑了翻转恢复力项，而忽略转动惯性力和阻尼力项，将翻转动力问题简化为静力问题。本文将式(10)考虑倾覆动力效应的方法称为动力倾覆分析法。

2.2 复模态分析方法

由于地震动记录往往具有较宽的频谱，能量分布较复杂，在此，首先针对图1所示的基础隔震剪力墙结构体系进行复频响分析。

对于具有非经典阻尼的振动系统，可采用复模态方法对其进行讨论。在式(7)基础上补充以下方程

(11)

则由式(7)、(11)可得状态方程

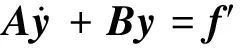
(12)

其中，

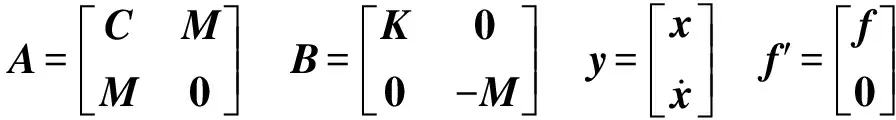
对于自由振动情况f′=0，于是有

(13)

求解该方程可得2对共轭复特征值及对应的共轭复特征向量，分别以矩阵形式表示为

*1λ*2]

(14)

(15)

式中，“*”表示共轭。

为进行由物理坐标到模态坐标的变换，令

y=Uq

(16)

其中，q=[q1q2q3q4]T，称为复模态坐标向量。

根据复模态理论，对应于状态方程的模态振型关于矩阵A、B有加权正交特性[10-11]。于是，可得由状态方程变换到复模态空间后的振动微分方程

*2])-1UTf′

(17)

其中，diag[a1…a*2]=UTAU。

若f′为频域激振力

(18)

则可设q的解为

q=Qejωt

(19)

代入式(17)，整理后得

*])-1UTF′

(20)

其中，E为4×4阶的单位阵。进而可得

*])-1UTF′

(21)

根据式(16)得

(22)

显然，{X}即为与前述微分方程式(7)中位移列向量对应的2×1复振幅列向量，且其表达式可写为

(23)

2.3 算例复频响分析

假设图1所示简化结构总质量m=22.845 t、宽度A=2.024 m、B=1.824 m、高度H=7.576 m，在结构底部四个角部位置分别布置一个LRB200铅芯支座，各支座屈服前刚度Ku=1.16×106N/m，屈服后刚度Kd=1.2×105N/m，水平等效刚度Keq=1.8×105N/m，竖向刚度KV=2.985×107N/m。参照以往试验结果，支座水平、竖向等效黏滞阻尼比分别取0.15、0.06。

为分析不同高宽比的情况，首先对高宽比的改变原则作如下说明：① 固定结构宽度A和B，改变结构高度H。结构质量随高宽比的变化同比例改变；② 隔震支座水平及竖向刚度随质量同比例改变。

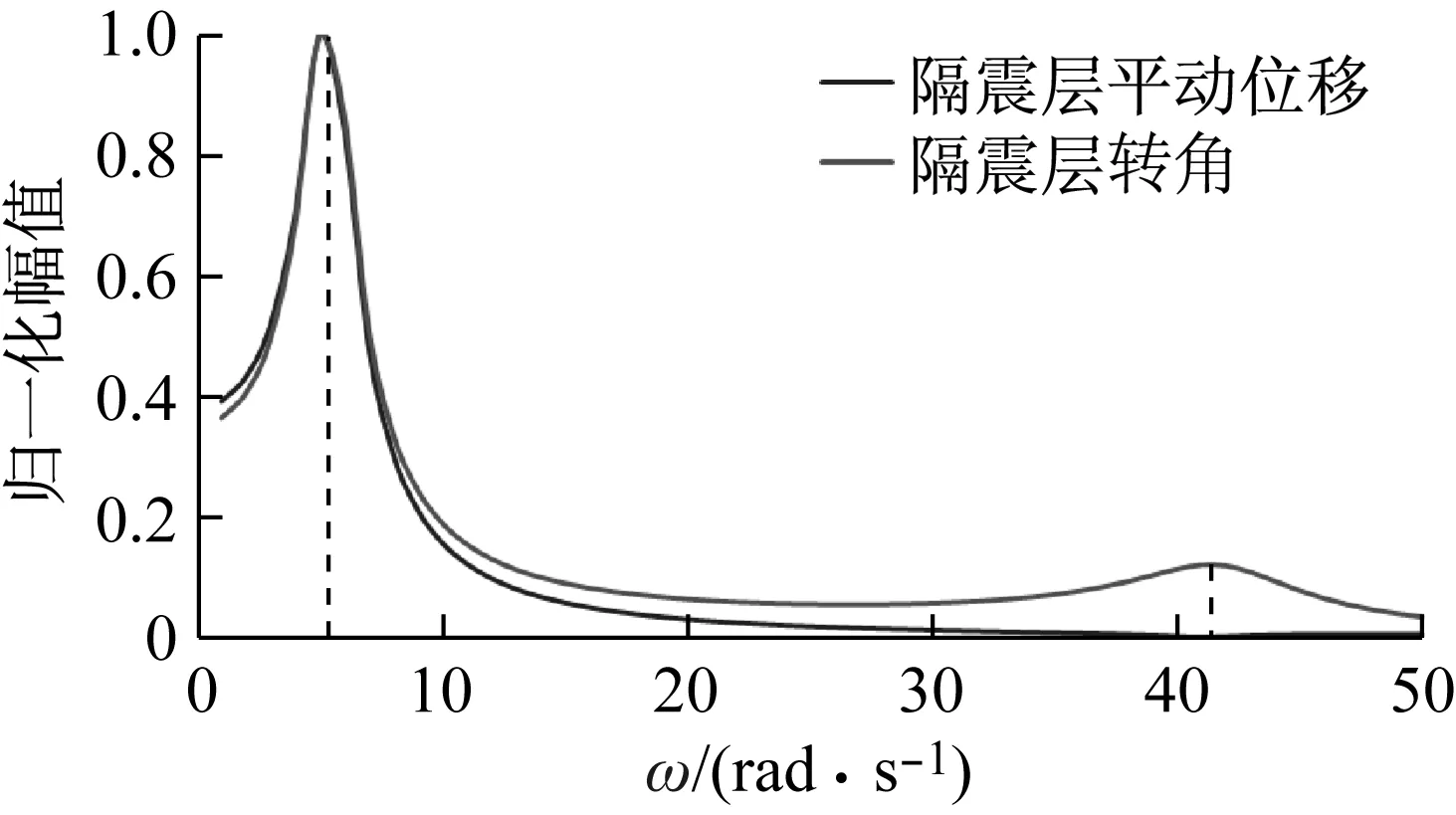
利用式 (23)，针对高宽比为3和6的两个结构计算复振幅的模，所得归一化的幅值频响曲线如图2所示。可见，两种高宽比结构对应频响曲线总体规律基本相同，保持激励力Fejωt幅值不变的情况下，随着激励频率ω的增大结构先后出现平动和转动共振，对应频率分别为ω1、ω2。平动共振时，平动位移及隔震层翻转角复频响幅值同步达到最大，转动共振引起的转角幅值远小于平动共振时的值。

(a) H/B=3

(b) H/B=6

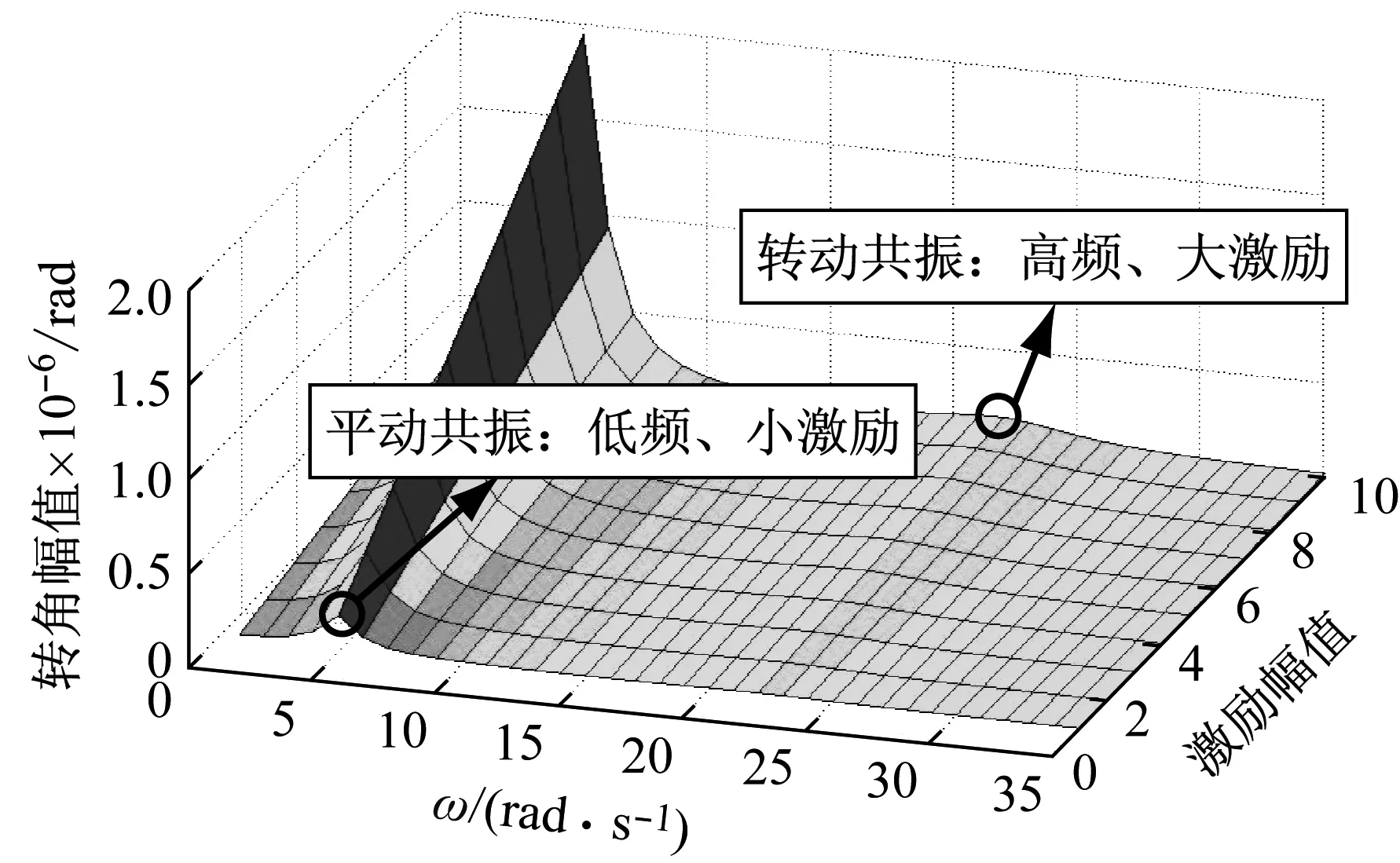
针对地震波中蕴含复杂频率分量的问题，对特定激励频率ω，给出从1到10递增的10个不同激励力幅值，进一步分析得到图3所示三维复频响曲面图。可见，对于平动和转动共振，其响应幅值均随着激励幅值的增大而增大；激励幅值增大到10的时候，转动共振引起的转角幅值才接近于激励幅值为1时平动共振所引起的值。

以上分析表明，结构在频率同于平动自振频率的地震波分量激励下，引起系统产生平动共振、出现最大平动位移幅值的同时，也使得隔震层翻转角幅值达到最大。可见，基础隔震剪力墙结构隔震层最大翻转角主要受平动共振频率对应的分量控制。

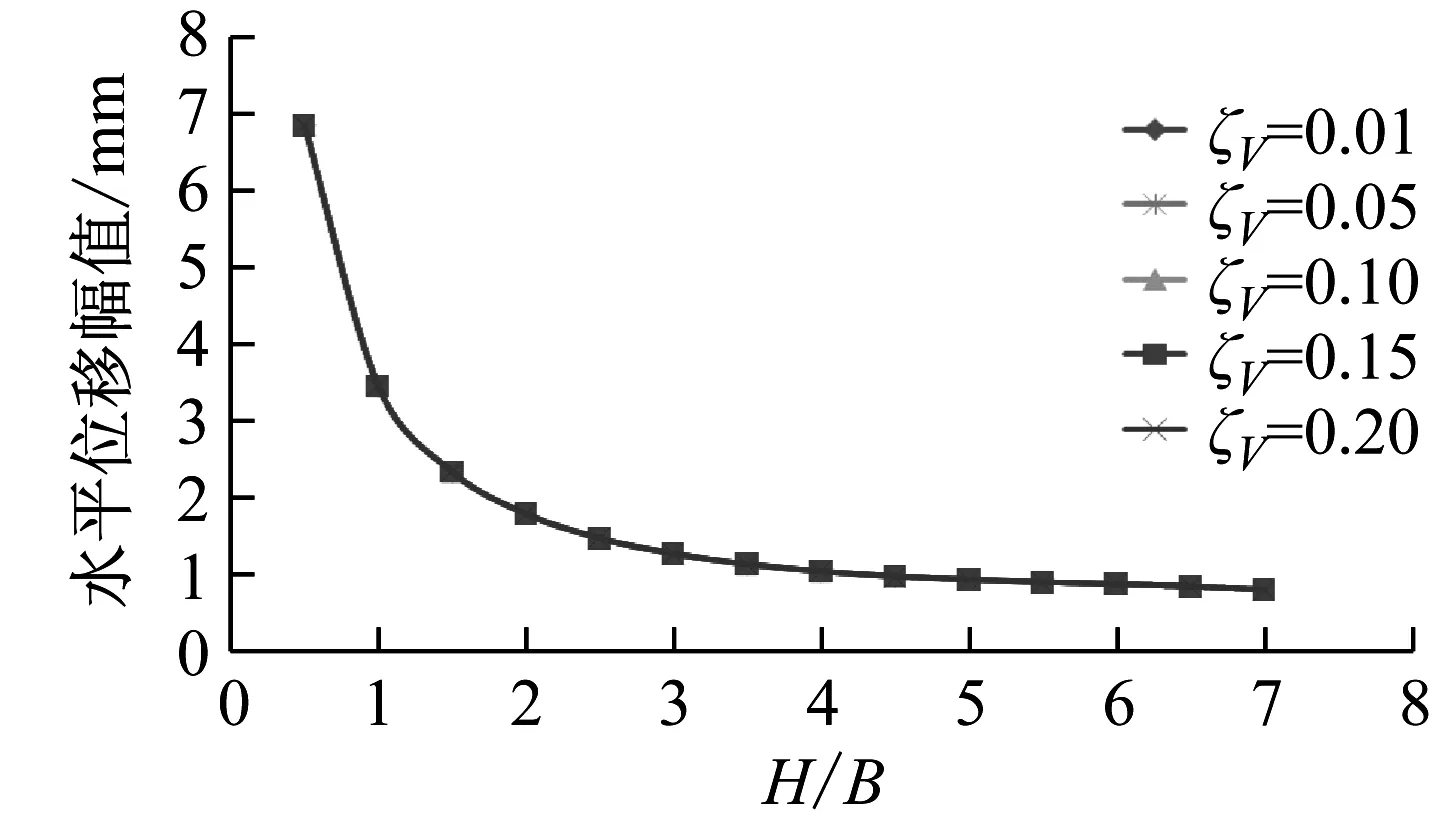
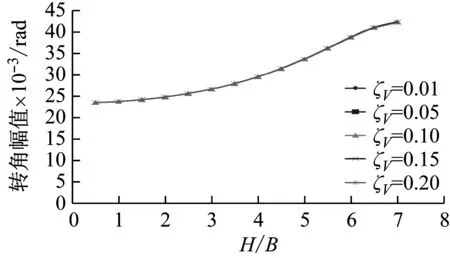
现对由支座竖向阻尼引起的隔震层整体转动阻尼的影响进行分析。保持激励力幅值及隔震支座水平等效阻尼比ζh=0.15不变，改变支座竖向等效阻尼比ζV，分析不同高宽比隔震结构复频响曲线平动共振峰对应的平动及翻转角位移幅值，所得曲线如图4所示。

(a) 隔震层转角三维幅频图(H/B=3)

(b) 隔震层转角三维幅频图(H/B=6)

(a) 水平相对位移

(b) 隔震层翻转角

由图4可见，隔震支座竖向阻尼比从0.01增大到0.2，不同高宽比结构水平位移及隔震层翻转角频响峰值几乎不会发生变化。由此表明，支座竖向阻尼，即隔震层转动阻尼对结构位移复频响幅值几乎没有影响，意味着可以不考虑式(15)中的Cθ项。

需要说明的是，上述分析中激励力幅值为任意特定值，因此，图4所示纵坐标的数值不具有一般性，但这不影响所讨论问题的一般规律。

3 考虑竖向地震作用及重力的高宽比限值

3.1 考虑翻转动能影响的高宽比限值公式

根据以上复频响分析结果，忽略式(15)中的Cθ项便得

(24)

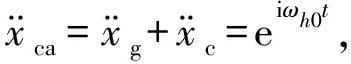
θ=θ0eiωh0t

(25a)

(25b)

其中，θ0为翻转角幅值。

将式(25)代入式(24)，移项整理后可得

(26)

于是，水平地震作用下，隔震层边缘支座轴力NBEh为

(27)

结构所受到的竖向地震作用标准值FEVK为[12]

FEVK=αVmaxGeq

(28)

式中，αVmax为竖向地震影响系数最大值，其数值取水平地震影响系数αmax的65%，Geq为上部结构等效总重力荷载，取重力荷载代表值的75%。则式(28)可重写为

FEVK=0.487 5αmaxG

(29)

于是，由竖向地震力产生的隔震层边缘支座竖向轴力NBEV可表达为下式

(30)

式中，KV为隔震层支座总竖向刚度。

对于隔震结构，重力二阶效应所产生的底部倾覆力矩可忽略[13-14]，那么，上部结构重力所引起的隔震层边缘支座轴力NBG可表达为下式

(31)

采用荷载基本组合计算边缘支座轴力

NB=γEhNBEh+γEVNBEV+γGNBG

(32)

式中，γEh、γEV、γG分别为水平、竖向地震作用、重力荷载分项系数。γEh、γEV分别取1.3、0.5，由于重力对结构倾覆是有利的，因此，γG取1。

以边缘支座不出现拉应力为上部结构倾覆的控制条件，则有

1.3NBEh+0.5FEVK≤NBG

(33)

将式(27)、(30)、(31)代入式(33)得

(34)

将隔震层整体转动刚度写为

(35)

其中，Ri=2li/B，KVi为第i排支座的竖向刚度，li为第i排支座中心到隔震层质心的距离(图5)，n为支座总排数。

图5 隔震层

对于上部结构刚度较大、质量沿高度分布较为均匀(不同于楼层质量集中的框架结构)的剪力墙结构，其绕质心的转动惯量Jc可近似表达为

(36)

将式(35)、(36)代入式(34)，移项整理后可得

(37a)

其中，

(37b)

可见，式(37a)中“≤”号左边为关于高宽比H/B的二次函数。由于系数a在αmax可能的取值范围内都大于零，因此，该二次函数图像为开口向上的抛物线，如图6所示，其中NB为边缘支座轴力。

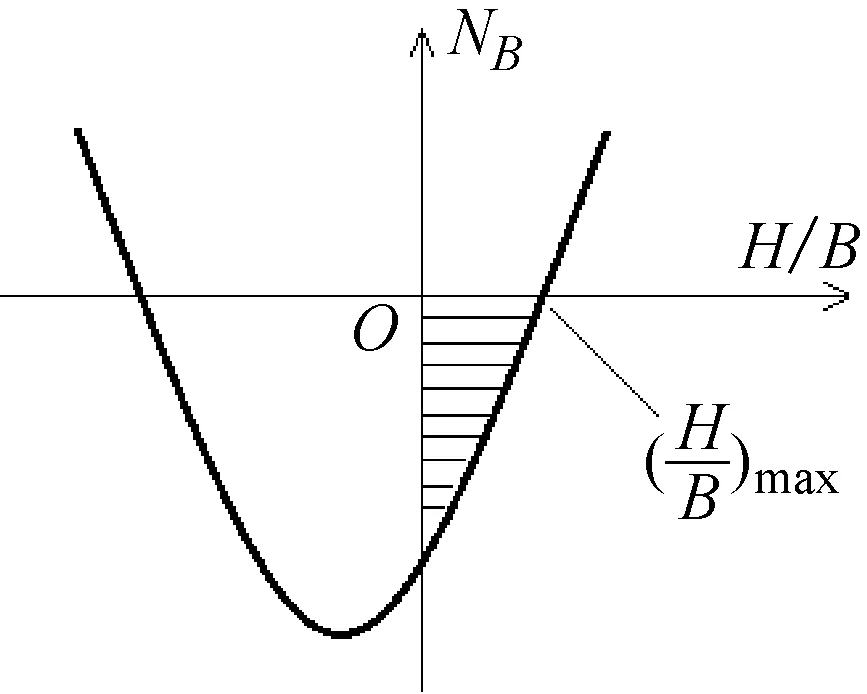
图6 隔震层边缘支座轴力随高宽比变化曲线(阴影部分)

令该二次函数等于零，求解方程所得正值解即为考虑转动动能影响的高宽比限值计算公式

(38)

式(38)中，隔震结构基本周期T=2π/ωh0，α1的值可根据反应谱确定，其为周期T、场地卓越周期Tg以及阻尼比ζ的函数。

3.2 上部结构质量及支座总竖向刚度的影响

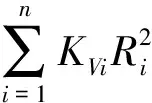
然而，尽管支座总竖向刚度与上部结构质量同比例变化的过程中，计算所得高宽比限值不发生变化，但计算结果大小却与二者比值有关。为阐述该比值的影响规律，现基于前述算例，支座总竖向刚度KV固定不变，而上部结构质量m依次由0.2m0增大到2m0(m0为算例上部结构质量)，则上述比值亦必然得到不同的值，以此分析高宽比限值的变化情况(其中，αmax=0.9，Tg=0.55)。图7为高宽比限值相对变化量(定义为不同质量比与m/m0=1时对应高宽比限值之间的相对变化量)随上部结构质量比的变化曲线。

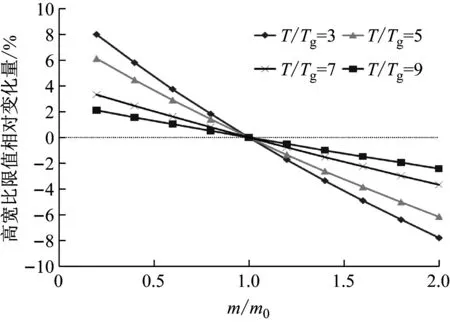
图7 (H/B)max随m/m0的变化曲线

由图7可见，支座总竖向刚度KV不变的情况下，高宽比限值随着上部结构质量比的增大而稍有减小，意味着KV/m比值越大、高宽比限值越大。特定场地周期Tg下，隔震结构周期越小，该比值的影响越显著。尽管总体变化幅度不太大，但也表明了，在其他设计条件不变的情况下，减轻上部结构质量、增大隔震支座总竖向刚度，对基础隔震剪力墙结构高宽比限值的提高是有利的。

3.3 结构周期的影响

采用前述算例分析7～9度罕遇地震作用下、不同场地卓越周期Tg对应的高宽比限值(H/B)max随周期比T/Tg的变化规律，可得图8所示的曲线，其中，7、8、9度对应αmax分别取0.5、0.9、1.4。

图8 (H/B)max随T/Tg的变化曲线

可以看出，不同烈度地震作用下，基础隔震剪力墙结构高宽比限值均随着周期的增大而增大。特定结构周期比下，烈度越大、高宽比限值越小。场地卓越周期越小、特定周期比对应的高宽比限值越小。各曲线在T=5Tg处均会出现明显的拐点，该拐点之前的曲线随周期增大快速上升，之后，显著趋于平缓。这是由于该拐点前后分别对应于我国加速度反应谱的曲线和直线下降段，而曲线段地震影响系数α随周期增大而快速减小，直线段则减小得相对较慢。

3.4 隔震层水平等效阻尼比的影响

改变算例中隔震层水平等效阻尼比ζh，使其在0.05～0.3内取不同的值，计算对应高宽比限值(αmax=0.9，Tg=0.55)。定义βn为不同阻尼比与ζh=0.15(0.15为算例阻尼比取值)时对应高宽比限值的比值，可得图9所示的曲线。

由图9可见，不同周期比T/Tg对应βn均随隔震层水平等效阻尼比的增大而增大。不同周期比对应的曲线基本重合，即随阻尼比变化的比例基本相同。

4 等效动力与静力倾覆分析法的比较

由前所述可知，等效动力与静力倾覆分析法的本质区别在于，计算水平地震作用所引起隔震层边缘支座轴力NBEh时，考虑转动惯性力与否。

为更为直观地对比两种方法的差异，现采用5条天然波El Centro、Holly、TR1、TRZ59、TRC64，2条人工波REN1、REN2共7条地震波作为激励(见图10)，加速度峰值为0.5 g，利用Newmark-β法，结合算例参数对图1所示不同高宽比(改变原则见2.3)的简化模型进行时程分析，隔震支座水平恢复力模型采用Bouc-Wen非线性滞回模型。具体如下：

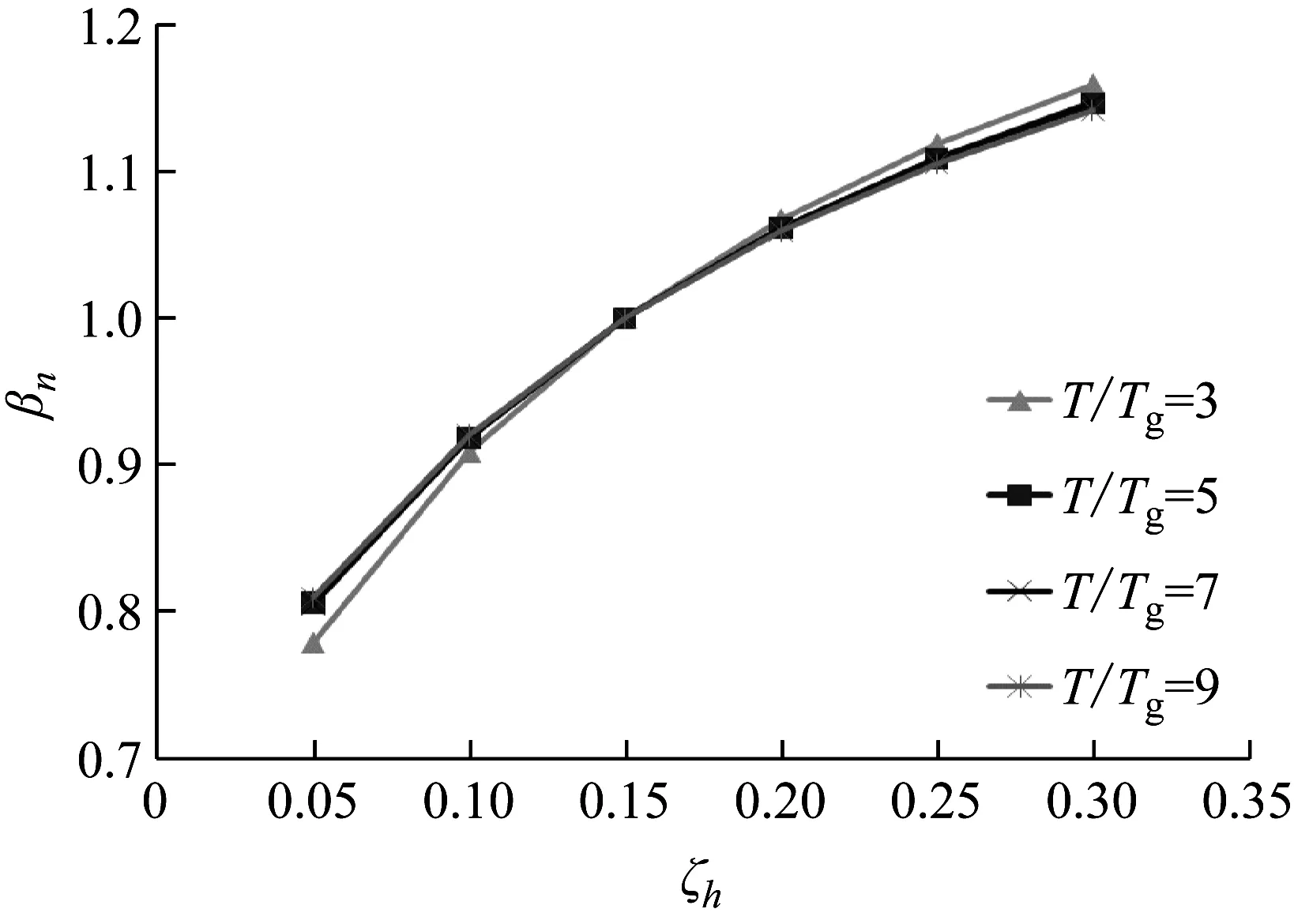
图9 βn随ζh的变化曲线

(1) 首先计算仅考虑平动的单自由度模型最大水平绝对加速度，并由此计算最大水平地震倾覆力矩；

(2) 将所得最大倾覆力矩分别代入静力法及动力法公式，计算NBEh的值；

(3) 对同时考虑平动及翻转的2自由度模型进行时程分析，直接计算隔震层翻转角，并根据该转角及支座竖向刚度计算相应NBEh值；

(4) 以第3步计算所得NBEh值为相对精确值，分析动力法及静力法计算结果相对于该值的相对偏差。

(a) El Centro波

(b) Holly波

(c) TR1波

(d) TRZ59波

(e) TRC64波

(f) REN1波

(g) REN2波

图11所示为各条波作用下，两种方法分析所得边缘支座最大轴力NBEh的平均值与相对精确值之间的相对偏差。可见，静力法和动力法计算结果平均偏差均为负偏差，计算结果均偏小。随着高宽比的增大，静力法计算结果偏差显著增大，高宽比为6时，该偏差已超过20%，计算结果偏小得多，不利于结构安全。动力法计算结果偏差明显小于静力法，且随着高宽比的增大，该偏差值有所减小。以上结果表明，考虑转动动能影响的动力法计算结果准确性显著高于静力法，且计算结果较静力法更偏于安全。

若式(33)中的NBEh按式(4)计算，则无需求解一元二次方程，直接经简单移项、整理后求解可得文献[4]所给出的高宽比限值等效静力计算式对比式(38)、(39)可见，相比较动力法而言，静力法并未考虑上部结构质量的影响。

图11 边缘支座轴力NBEh平均相对偏差

(39)

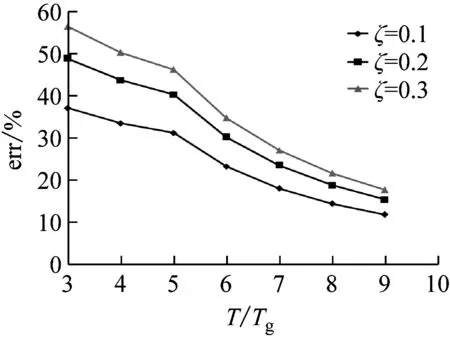
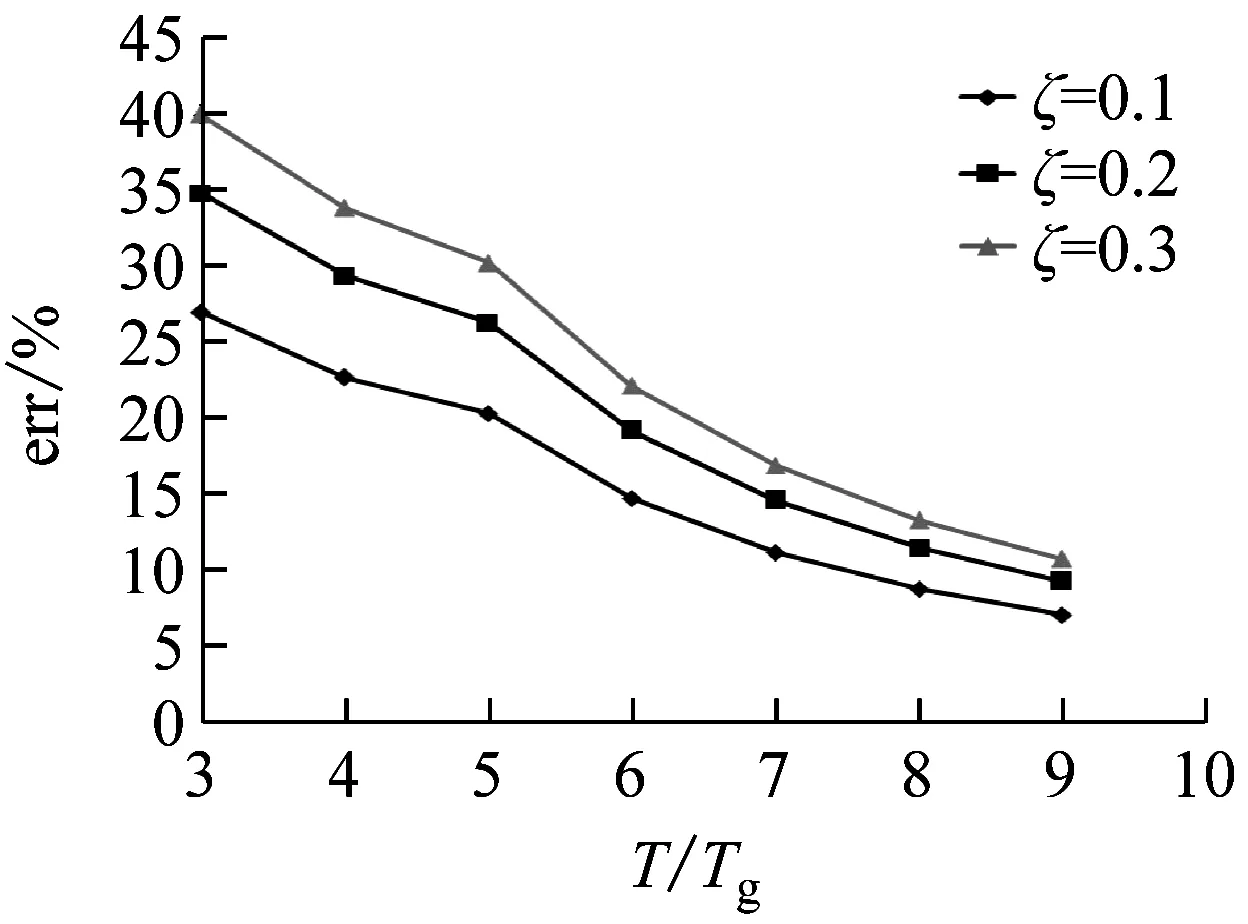
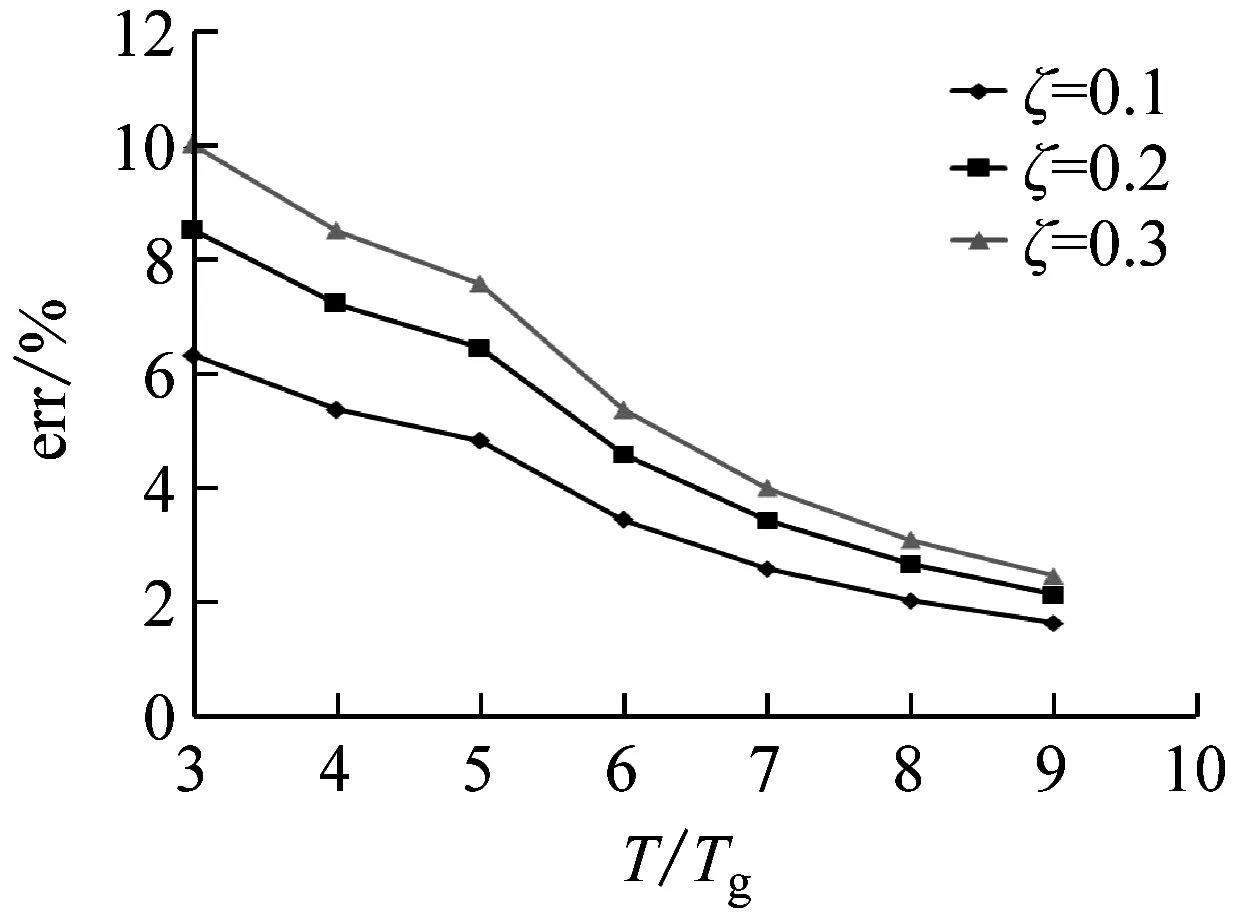
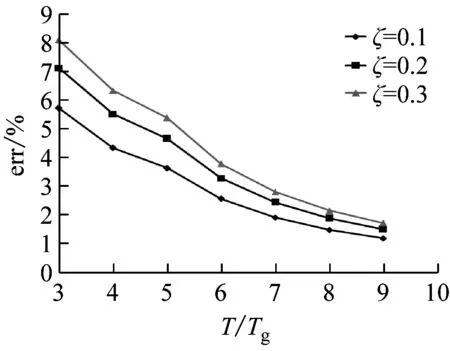
现根据算例所给支座布置方式以及相关参数，分别利用式(38)、(39)计算基础隔震剪力墙结构以支座不受拉为控制条件的高宽比限值，以对比两种方法的差异。图12表示不同阻尼比、场地周期和烈度对应两种方法计算高宽比限值相对偏差err与隔震后结构基本周期比的关系曲线。其中err=(静力法结果-动力法结果)×100/动力法结果。

由图12可见，采用静力法计算所得以支座不受拉为控制条件的高宽比限值，相对于动力法结果均为正偏差，说明忽略上部结构转动动能将导致高宽比限值偏大。同时也可看出，阻尼比越大，两种方法计算结果偏差越大。随着结构周期的增大(隔震层水平刚度减小)，系统趋于以平动为主，翻转动能的影响也随之减小，因而，该偏差值逐渐减小。

(a) αmax=0.5、Tg=0.3 s

(b) αmax=0.5、Tg=0.45 s

(c) αmax=0.5、Tg=0.65 s

(d) αmax=0.9、Tg=0.3 s

(e) αmax=0.9、Tg=0.45 s

(f) αmax=0.9、Tg=0.65 s

(g) αmax=1.4、Tg=0.3 s

(h) αmax=1.4、Tg=0.45 s

(i) αmax=1.4、Tg=0.65 s

烈度越低(αmax越小)，偏差越大，反之则反。对应同样的场地周期Tg=0.3 s，当αmax=0.5(7度罕遇地震)、ζ=0.1、T/Tg=3时，偏差达70%，而当αmax=1.4(9度罕遇地震)时，对应偏差不到14%。这意味着，烈度越低，忽略翻转动能所造成的影响越发显著。特定烈度地震作用下，随着场地周期Tg的增大，相同周期比T/Tg对应的偏差趋于减小。这是由于地震动周期越长，周期比不变也即意味着隔震结构周期将会更长，则结构越是以平动为主，假设周期无限制地增大到一定程度时，结构将不再翻转，那么，翻转动能的影响几乎不存在。

综上所述，基础隔震高层剪力墙结构的上部结构翻转动能对高宽比限值具有显著的影响。同时，以上分析也表明，分析隔震结构高宽比限值时，应当充分考虑场地条件、地震分组、结构周期、阻尼比等因素的影响。

需要进一步补充说明的是，由前述对周期、阻尼比的影响分析可以看到，增大周期和阻尼比均有利于高宽比限值的提高。然而，周期太大必然导致隔震层侧移过大，而增大隔震层等效阻尼比势必降低隔震效能[15]。实际隔震结构高宽比限值的确定尚需综合考虑上述问题。本文旨在对比分析上部剪力墙结构整体翻转动能的影响，所给高宽比限值均以支座不受拉为控制条件而确定。

5 结 论

通过以上分析，可得出如下结论：

(1) 上部结构翻转动能对基础隔震剪力墙结构以支座不受拉为控制条件的高宽比限值的影响不容忽视。本文提出的考虑翻转动能影响的动力倾覆分析法较仅考虑平动动能的等效静力法更为准确，且更偏于安全。

(2) 等效静力法相对于动力法计算结果偏差，随着地震烈度、隔震后结构周期、场地卓越周期的增大而减小，随隔震层水平等效阻尼比的增大而增大。

(3) 在其他设计条件不变的情况下，减轻上部结构质量、增大隔震支座总竖向刚度，有利于基础隔震剪力墙结构高宽比限值的提高。

(4) 分析基础隔震剪力墙结构高宽比限值时，应当充分考虑场地条件、地震分组、结构周期、阻尼比等因素的影响。