预应力混凝土曲线刚构桥的空间效应研究
张晔芝,左维,杨毅
预应力混凝土曲线刚构桥的空间效应研究
张晔芝,左维,杨毅
(中南大学 土木工程学院,湖南 长沙 410075)
为研究曲线刚构桥变形和受力状态以及空间效应的相关规律,对一座主跨145 m,曲率半径600 m的5跨连续预应力曲线刚构桥模拟整个施工过程,采用空间梁格法进行有限元分析。研究结果表明:墩身处于轴压和切向、法向双向弯曲联合作用状态,梁体处于竖弯、横弯和扭转联合作用状态。由此造成梁体竖向位移和应力横向分布的不均匀性,且还有法向位移。悬臂浇筑各阶段,法向位移指向曲率中心侧,梁体竖向位移内侧大、外侧小,最大悬臂状态下,内侧竖向位移比中心线处增大49%,外侧比中心线处减小36%。应力也有较大的差别。二恒、活载作用下的空间效应规律正好与一恒作用下相反。本文研究成果可为今后曲线桥的设计和计算提供理论依据。
预应力曲线刚构桥;空间梁格法;有限元;空间效应

在某些特殊地形地质条件下,建造一座曲线梁桥可以减少施工难度,降低工程造价,还能增加景观效果。近年来曲线梁桥的应用有增多的趋势,研究也随着应用的增多而增多。现有研究方法绝大多数都是有限单元法中的曲梁法[1−12]。王帆等[13]对一座跨度为(80+2×120+80) m,曲率半径为800 m的双线铁路曲线连续刚构桥进行研究,得出结论:弯梁桥中存在横向变形和扭矩,但数值都较小。何培楷[14]以某跨度为(75.25+140+75.25) m的连续刚构桥为背景,用曲梁法研究了曲率对大跨度曲线刚构桥变形的影响,得出结论:变形与曲率半径呈对数关系变化,曲梁半径越小,活载对竖向位移的影响明显,当曲率半径小于2 500 m时,空间曲梁法计算活载挠度较平面直梁法挠度值至少增加30%。这一结论令人难以置信。为了寻求相关规律,本文采用空间梁格法对桐溪路曲线连续刚构桥(TX桥)的变形和受力状态以及空间效应进行研究。
1 空间梁格法有限元分析方法
1.1 施工方法
桐溪路曲线连续刚构桥(TX桥)因受地质条件(溶洞)的限制,设计成曲率半径为600 m,孔跨布置为(15+55.5+145+55.5+15) m的全预应力混凝土曲线连续刚构桥。主跨即145 m,跨左右两侧刚构墩墩高分别为24 m(2号墩)和18 m(3号墩)。TX桥采用悬臂浇筑跨中合拢的施工方法,两端15 m边跨采用满堂支架施工;刚构墩外侧的55.5 m次边跨和145 m主跨梁体采用不对称悬臂浇筑。次边跨分为12个梁段,主跨分为16个梁段悬臂浇筑。每个刚构墩两端悬臂浇筑完12号块后,次边跨侧梁体在1号和4号墩上与边跨合拢。然后,刚构墩在主跨侧单悬臂浇筑至16号块,再在主跨跨中合拢。桥面全宽22.6 m,双向城-A四车道。图1~3为该桥的视图。

单位:cm

图2 TX桥俯视图
1.2 梁格法有限元模拟方法
采用Maidas/civil通用软件对TX桥建立空间梁格法有限元模型。将该桥梁体横桥向分割成5个条带,每一条带称为一条纵梁。顺桥向每1.5~2 m划分为一个条块,每一条块等效成一根横梁。每一根横梁的轴线是法线方向的直线,梁体的宽度内小外大。从实际的梁体分割到的横向条块只有顶板和底板,将每一条块的顶板和底板用很薄的腹板上下连起来,等效为一片工字梁,该工字梁的面积和抗弯刚度都与原来的条块完全相同[15]。纵梁与横梁在节点相交处刚结,这样处理后,梁体等效成了一个格子梁。

单位:m
有限元分析中将梁体的自重都等效作用于纵梁上,横梁只有刚度而没有自重。每一根纵、横梁都分成许多空间梁单元,刚构墩墩身和每一根桩基也都采用空间梁单元,用弹簧单元考虑桩土的相互作用。梁单元每节点有6个自由度(即,,,,和)。图4为TX桥空间曲线梁格法的有限元模型。

图4 空间梁格法有限元模型
2 TX桥空间效应分析
2.1 悬臂施工阶段的空间效应分析
用空间曲线梁格法作有限元分析,得到梁体和刚构墩各阶段变形。图5为2刚构墩双侧浇筑完12号块梁体的竖向位移曲线,12号块为每墩双侧最大悬臂状态。内侧是指梁体靠近曲率中心侧,外侧梁体为背离曲率中心侧。图中粗实线、细实线和粗虚线分别为梁体内侧、中心和外侧的竖向位移曲线,下同。图6为浇筑完主跨16号块梁体的竖向位移曲线,此时边跨早已合拢,主跨处于最大悬臂状态。图5和图6中2刚构墩及墩身两侧的位移都略有不同,这是因为12号块梁体自重主跨侧大于边跨侧,2号墩墩高高于3号墩。表1为悬臂施工各阶段梁体内、中、外各处的竖向位移值。图表中的位移是指悬臂浇筑过程中各块的累计位移,即第块的位移是从浇筑第块起,其后每一块的浇筑所引起的第块位移增量的总和。梁体的竖向位移以向上为正,向下为负;法向位移以内侧向外侧移动为正,反之为负。

图5 双侧浇筑完12号块梁体竖向位移(以向上为正)

图6 浇筑完主跨16号块的竖向位移
由图5~6可知,各阶段梁体竖向位移的横向分布都有明显的不均匀性;竖向位移内侧大、外侧小。梁体浇筑完主跨16号块后,墩顶梁体内、外侧竖向位移分别是中线的1.48倍、0.64倍;主跨3/8处,内、外侧竖向位移分别是中线的1.08倍和 0.92倍。
图7为双侧浇筑完12号块、浇筑完主跨16号块状态下梁体法向位移曲线。表2为悬臂施工各阶段梁体法向位移。

表1 悬臂施工各阶段梁体内、中、外各处的竖向位移

图7 梁体法向位移(以向外为正)

表2 悬臂施工各阶段梁体法向位移
由图7及表2可知,梁体法向位移向内侧移动,双侧最大悬臂状态下梁体墩顶处法向向内移动了3.74 mm;浇筑完主跨16号块阶段下梁体墩顶处法向向内移动了8.57 mm;最大法向位移向内移动了13.76 mm,发生在主跨/4处。
图8和图9分别为悬臂施工各阶段2号墩的切向、法向位移曲线。切向位移是沿着梁体各纵梁的切线方向,以2号墩向主跨侧移动为正,反之为负。
由图可见,悬臂浇筑各阶段,墩身的法向位移向内侧移动,切向位移向主跨侧移动。浇筑完主跨16号块状态下,墩顶法向位移最大值为6.02 mm;切向位移最大值为20.59 mm,法向位移约为切向位移的30%。

图8 悬臂施工各阶段2号墩切向位移

图9 悬臂施工各阶段2号墩法向位移
梁体最大悬臂状态下,墩身截面4个角点沿墩高的应力分布曲线见图10。墩身各个截面上4个角点的应力各不相同。

图10 墩身4角点应力分布曲线
梁体内、中、外3条腹板顶板上缘的应力曲线见图11(仅画出桥梁左半边)。梁体同一截面上不同位置的应力是有差别的,分布情况较为复杂;差别最大发生在墩顶和主跨跨中附近。这种差别除了由梁体自重作用下的变形引起外,还与预应力筋横向分布不一致有关。
综上所述,在悬臂施工阶段,梁体的空间效应是很明显的。墩身处于轴压和切向、法向双向弯曲联合作用状态,切向向主跨侧弯曲,法向向曲率中心侧弯曲。梁体处于向下竖弯、向内横弯和扭转联合作用状态,从而造成了梁体既有竖向位移,又有横向位移,而且竖向位移截面上分布不均匀,内侧大,外侧小。

图11 梁体腹板顶板上缘应力曲线
2.2 二恒作用下的空间效应
二期恒载包括10 cm沥青铺装、人行道板、防撞护栏等,合计顺桥向87.5 kN/m均布。有限元分析中将二恒按每片纵梁的顶板面积分配到各片纵梁上[16−18]。图12和图13分别为二恒作用下的梁体竖向位移与法向位移。表3列出主梁一恒、二恒和一恒、二恒共同作用下竖向、法向位移值。

图12 二恒作用下的梁体竖向位移

图13 二恒作用下的梁体法向位移
图14分别为二恒作用下2号墩法向位移曲线。
由图14和表3可见:二期恒载作用下,TX桥的空间效应规律正好与一恒作用下的相反;梁体、墩身法向背向曲率中心侧移动,梁体竖向位移外侧大、内侧小,内、外侧分别是中心线处的0.83倍和1.18倍。二期恒载引起的位移远小于一恒。所以一恒和二恒组合作用下,墩身、梁体的位移和应力由一恒主导,空间效应与一恒相同,但略有减小。由于二期恒载引起的应力很小,不再列出。

表3 梁体各处位移值

图14 二恒作用下墩身法向位移曲线
2.3 活载作用下的空间效应
活载为城A,按最不利活载布载[19−20]。图15为活载作用下梁体的内、中、外竖向位移包络图。图16为活载作用下梁体的法向位移包络图。表4列出活载作用下主梁各处位移值。
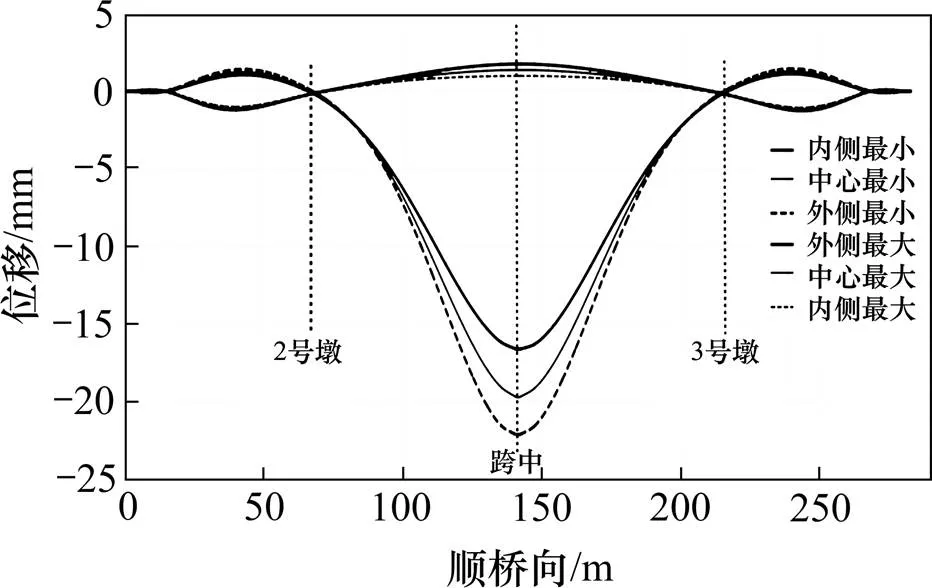
图15 活载作用下梁体竖向位移包络图

图16 活载作用下梁体法向位移包络图

表4 活载作用下主梁各处位移
图17和图18分别为活载作用下墩身的切向、法向位移曲线。
由图17~18和表4可见,活载作用下梁体、墩身的位移和空间效应与二期恒载的基本相同,不仅远小于一期恒载作用下的值,而且还小于二期恒载作用下的值。

图17 活载作用下墩身切向位移

图18 活载作用下墩身法向位移
3 结论
1) TX桥的空间效应很明显。墩身处于轴压和切向、法向双向弯曲联合作用状态;梁体处于竖弯、横弯和扭转联合作用状态。位移和应力的分布较为复杂。
2) 梁体悬臂浇筑各阶段,梁体和墩身法向向曲率中心侧移动。梁体竖向挠度内侧大外侧小;最大悬臂状态下,内侧比中心线处最大增大了49%,外侧比中心线处最小减小了36%;不同位置截面处的差别有所不同。墩身、梁体的应力各截面上的分布也各不相同。
3) 二恒和活载作用下的空间效应规律正好与悬臂浇筑阶段相反,梁体和墩身法向背向曲率中心侧移动。梁体竖向挠度内侧小外侧大;二恒作用下,内侧比中心线处最小减小了17%,外侧比中心线处最大增大了18%;不同位置截面处的差别有所不同。墩身、梁体的应力各截面上的分布也各不相同。
4) 由于二恒和活载作用下引起的位移和应力远小于一期恒载,所以三者共同作用下的位移和应力由一期恒载起主导作用,空间效应的趋势和一期恒载相同,但法向位移和竖向位移的内外差都略有减小,但差别仍然明显。
[1] 白鹏宇, 丁少凌, 彭元诚, 等. 小半径曲线刚构−连续梁桥单箱双室主梁合理构造设计研究[J]. 世界桥梁, 2018, 46(3): 7−11. BAI Pengyu, DING Shaoling, PENG Yuancheng, et al. Study on reasonable structural design of single box and double chamber main girders of small radius curved rigid frame-continuous girder bridge[J]. World Bridge, 2018, 46(3): 7−11.
[2] 宋吉. 预应力混凝土连续梁桥施工阶段受力分析研究[D]. 重庆:重庆交通大学, 2015. SONG Ji. Force analysis and study of the construction stage of the prestressed concrete continuous beam bridge[D]. Chongqing: Chongqing Jiaotong University, 2015.
[3] 董旭. 预应力混凝土连续梁桥施工控制研究[D]. 西安:西安建筑科技大学, 2015. DONG Xu. Research on construction control of prestressed concrete continuous girder bridge[D]. Xi’an: Xi’an University of Architecture and Technology, 2015.
[4] 姜敏. 预应力混凝土连续梁桥施工控制计算[D]. 石家庄: 石家庄铁道大学, 2015. JIANG Min. Construction control calculation of prestressed concrete continuous girder bridge[D]. Shijiazhuang: Shijiazhuang Railway University, 2015.
[5] 卢钢. 小半径曲线预应力混凝土连续梁桥设计[J]. 市政技术, 2014, 32(3): 44−46, 50. LU Gang. Design of prestressed concrete continuous girder bridge with small radius curve[J]. Municipal Technology, 2014, 32(3): 44−46, 50.
[6] 汤刚. 曲线连续刚构桥结构力学行为研究[D]. 长沙: 长沙理工大学, 2016. TANG Gang. Research on mechanical behavior of curved continuous rigid frame Bridges[D]. Changsha: Changsha University of Science and Technology, 2016.
[7] 陈淮, 颜浩杰, 李杰, 等. 曲率半径变化对高墩大跨连续刚构桥静力性能的影响[J]. 铁道科学与工程学报, 2013, 10(1): 6−10. CHEN Huai, YAN Haojie, LI Jie, et al. Effect of curvature radius change on static performance of long- span continuous rigid frame bridge with high piers[J]. Journal of Railway Science and Engineering, 2013, 10(1): 6−10.
[8] 赵越. 大跨径曲线连续刚构桥不同曲率受力比较分析[J]. 市政技术, 2014, 32(3): 61−63. ZHAO Yue. Comparative analysis of forces at different curvature of long-span curved continuous rigid frame bridges[J]. Municipal Technology, 2014, 32(3): 61−63.
[9] 吕海燕, 马锋, 王朋. 高墩大跨PC曲线连续刚构桥受力和变形研究[J]. 长沙铁道学院学报(社会科学版), 2011, 12(4): 214−215. LU Haiyan, MA Feng, WANG Peng. Research on force and deformation of high-dun long-span PC curved continuous rigid frame bridge[J]. Journal of Changsha Railway University (Social Science Edition), 2011, 12(4): 214−215.
[10] 张志新. 高墩曲线连续刚构箱梁桥空间行为研究[D].西安: 长安大学, 2011. ZHANG Zhixin. Study on spatial behavior of curved continuous rigid frame box girder bridge with high pier[D]. Xi’an: Chang’an University, 2011.
[11] 刘泽宇, 李雄. 公路曲线梁桥设计计算[J]. 建筑技术开发, 2018, 45(6): 101−102. LIU Zeyu, LI Xiong. Design and calculation of curved girder bridge of highway[J]. Development of Construction Technology, 2018, 45(6): 101−102.
[12] 谭威, 张景, 夏桂云. 考虑剪切变形影响的连续曲线梁受力分析[J]. 交通科学与工程, 2017, 33(2): 23−30. TAN Wei, ZHANG Jing, XIA Guiyun. Stress analysis of continuous curved beams considering shear deformation [J]. Transportation Science and Engineering, 2017, 33(2): 23−30.
[13] 王帆, 祝兵, 窦胜谭, 等. 曲线连续刚构桥的变形和受力特性分析[J]. 重庆交通大学学报(自然科学版), 2013, 32(增1): 864−868. WANG Fan, ZHU Bing, DOU Shengtan, et al. Analysis on deformation and mechanical characteristics of curved continuous rigid frame bridges[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2013, 32(Suppl l): 864−868.
[14] 何培楷. 大跨径曲线刚构桥曲率半径对其变形的影响研究. 中国公路学会、国际道路联盟(IRF)、美国交通研究委员会(TRB). 第六届中国公路科技创新高层论坛论文集(下册)[C]// 中国公路学会、国际道路联盟(IRF)、美国交通研究委员会(TRB): 中国公路学会, 2013: 547−551. HE Peikai. Long-span rigid frame bridge curvature radius it. Studies on the influence of the deformation of China highway society, international road federation (IRF), the transportation research board (TRB). The sixth China road top BBS on science and technology innovation (part II)[C]// China Highway Society, International Road Federation (IRF), the Transportation Research Board (TRB): China Highway Society, 2013: 547−551.
[15] 吴俊虢, 刘汉锡, 王惠队, 等. 连续刚构桥主梁设计参数优化方法研究[J]. 铁道科学与工程学报, 2017, 14(7): 1473−1480. WU Junguo, LIU Hanxi, WANG Huidui, et al. Research on optimization method of main girder design parameters of continuous rigid frame bridge[J]. Journal of Railway Science and Engineering, 2017, 14(7): 1473−1480.
[16] 孙志伟, 刘英, 邬晓光, 等. 连续刚构宽箱梁剪力滞效应分析及有效分布宽度研究[J]. 铁道科学与工程学报, 2016,13(7): 1347−1351. SUN Zhiwei, LIU Ying, WU Xiaoguang, et al. Analysis of shear lag effect and effective distribution width of continuous rigid frame wide box girder[J]. Journal of Railway Science and Engineering, 2016, 13(7): 1347− 1351.
[17] DAI Fan, HE Jian, YOU Shang, et al, The effect of asymmetric reinforcement on curved bridge[C]// Proceedings the 5th International conference on Advanced Design and Manufacturing Engineering, 2005.
[18] LIU H, DU J, CHANG X, et al. Closure schemes of Multi-span continuous rigid frame bridges[C]// International Conference on Mechanic Automation and Control Engineering. IEEE, 2010: 780−783.
[19] FENG J, DONG J. Study on the seismic behavior of the large-span, curved, continuous, rigid frame bridge under different curvature radius[C]// Asia Pacific Transportation Development Conference, 2014: 594−601.
[20] GU Y, ZHUO W. Study on applicability of a pushover analysis method for seismic analysis of long-span continuous rigid frame bridge with high piers[J]. Journal of Computational & Theoretical Nanoscience, 2012, 9(1): 729−734.
Study on spatial effect of prestressed concrete curved rigid frame bridge
ZHANG Yezhi, ZUO Wei, YANG Yi
(School of Civil Engineering, Central South University, Changsha 410075, China)
In order to study the relationship between deformation, stress state and spatial effect of curved rigid frame bridge, the whole construction process and using three dimension grillage beam method, finite element analysis has been completed of a 5-span continuous prestressed curved rigid frame bridge with 145 m main span and 600 m radius of curvature. The deformation , force state and space effect were studied. The results show that the piers are under the combined action of axial pressure, tangential and normal bending, and the beam is under the combined action of vertical bending, transverse bending and torsion, which caused the difference of vertical displacement and stress on the transverse direction of the beam, and as well as caused the normal displacement of the beam. In each stage of cantilever constrction, the normal displacement points to the curvature center, and the inside vertical displacements of the beam are larger than that of the outside. Under the maximum cantilever state, the inside vertical displacements are 48% larger than that of the center, and the outside vertical displacements are 36% smaller than that of the center. The difference of stresses are also considerable. The research of this paper will provide theoretical basis for the design and calculation of curved bridge in the future.
prestressed curved rigid frame bridge; three dimension grillage beam method; finite element; spatial effect
U448.36
A
1672 − 7029(2019)09−2248 − 08
10.19713/j.cnki.43−1423/u.2019.09.016
2018−09−15
湖南湘江新区投资集团有限公司投资项目(2017-9-25-220)
张晔芝(1973−),男,上海人,副教授,博士,从事桥梁工程研究;E−mail:zhangyz824@163.com
(编辑 涂鹏)

