基于数值振荡消除下自耦变压器建模与谐波机理分析

董唯光，辛国庆，高锋阳，吕晓强

基于数值振荡消除下自耦变压器建模与谐波机理分析

董唯光1，辛国庆1，高锋阳1，吕晓强2

(1. 兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2. 国家电网甘肃检修公司，甘肃 酒泉 735000)

对自耦变压器进行模型的理论分析并搭建仿真模型，但由于绕组间磁的耦合作用，仿真时出现数值振荡并造成图像失真，为此推导并提出一种新型阻尼梯形法来抑制数值振荡。先对阻尼因子进行预测估值，再加入辅助阻尼因子进行校正，最后对励磁电流i进行振荡补偿。仿真结果表明：搭建的模型可以清晰地反映自耦变压器在运行时出现的谐波波形，为自耦变压器出现谐波时进行故障预警提供了参考依据。

高速铁路；自耦变压器；数值振荡；阻尼梯形算法；模型仿真；谐波分析

随着我国高速列车的发展，对供电系统的电能质量要求也越来越高，自耦变压器(auto transformer AT)作为牵引供电系统中核心设备，由于存在“励磁涌流”以及“漏抗”等，产生了大量的髙次谐波。目前，对高速铁路牵引供电系统的研究主要集中在数学模型分析[1]和计算机仿真分析[2]。Hanmin等[3]对自耦变压器进行模型的搭建，但忽略自耦变压器中高压绕组间电的联系,仅考虑磁的耦合作用，用普通变压器模型代替自耦变压器进行暂态仿真，不能很好地体现出自耦变压器中的谐波问题。何正友等[4−6]建立通用的机车−牵引网联合仿真模型，考虑自耦变压器(autotransformer，AT)漏抗及牵引网多导体线间的互电感、互电容耦合的情况，从牵引网谐波放大倍数的角度考察谐振以及谐波放大特性。徐晨博等[7]对变压器进行在线监测系统的开发与应用，搭建了仿真模型并投入使用；Kritsada等[8]提出一种基于电流的Newton-Raphson潮流方法，用于自耦变压器(AT)铁路供电系统，并通过增广变压器导纳阵解决其奇异性问题；Worku等[9]提出一种替代的，更优越的2×25 kV牵引供电系统并进行了建模和分析，包括牵引负荷，变电站电力变压器，自耦变压器(AT)，接触网线路阻抗等；但都没有对自耦变压器进行单独的建模和谐波传输特性进行研究。本文基于Matlab/Simulink搭建通用的自耦变压器仿真模型，将自耦变压器中的电路与磁路结合起来考虑，采用一种修正后新的阻尼梯形法消除数值振荡，对自耦变压器中由于“励磁涌流”及“漏抗”等原因产生的谐波电压进行仿真分析，观测谐波波形，得到大量的谐波数据，为进一步谐波的抑制提供数据。

1 高速铁路供电系统

供电系统运行的基本原理为：牵引变电站为整个牵引供电系统提供电源，电流从牵引变电站流出，通过接触网给高速列车提供电能，然后通过负馈线流回牵引变电站[11]；我国铁路的供电方式主要有：BT(吸流变压器)供电方式、AT(自耦变压器)供电方式和TR(直接供电)方式[5]。由于高速铁路功率大，牵引网电流较大，因此，采用功率输送能力最强的AT供电方式，其典型的AT供电系统如图1所示。

AT供电系统主要由牵引变电站，自耦变压器AT，牵引线T，负馈线F，钢轨R与大地以及高速列车组成，供电系统电压为±27.5 kV交流制[1]。

图1 AT供电系统图

2 自耦变压器模型理论分析

2.1 自耦变压器接线方式

自耦变压器常见的接线方式主要有：1) 单相V/V接线；2) 三相V/V接线；3) Scott接线；4) V/X接线。张淇铭等[5, 12]分别对V/X接线进行研究，从工程应用的角度和经济性说明了选择V/X接线的必要性与合理性。综合考虑，本文采用V/X接线自耦变压器。

2.2 自耦变压器内部结构

高速列车中使用的自耦变压器三相之间相对来说独立，内部结构一致，其参数也仅有微小差别，因此，对三相三绕组自耦变压器进行数学参数研究时，可将三相简化为单相三绕组自耦变压器来进行参数计算[10]。

根据自耦变压器的内部结构，可以等效出单相三绕组自耦变压器的电路图，如图2所示。

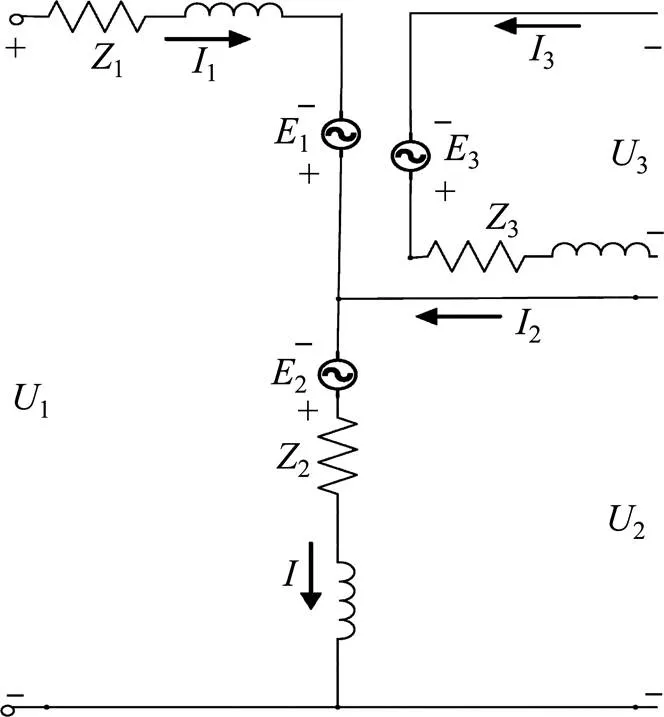
图2 单相三绕组自耦变压器等效电路图

在图3中，1和1表示外加电压电流；2和2是中压侧绕组电压电流；3和3是低压侧绕组电压电流；是公共绕组中的电流；1，2和3分别为串联绕组，中压侧绕组以及低压侧绕组的电动势；1，2和3为串联绕组，中压侧绕组以及低压侧绕组的漏阻抗；假设c为激励电流，c为高压侧电动势，各物理量在图中均规定了正方向。

2.3 电路模型的推导

由图2电路图中所规定的正方向，根据电路基础中的基尔霍夫定律，可列出电压回路方程如下所示：

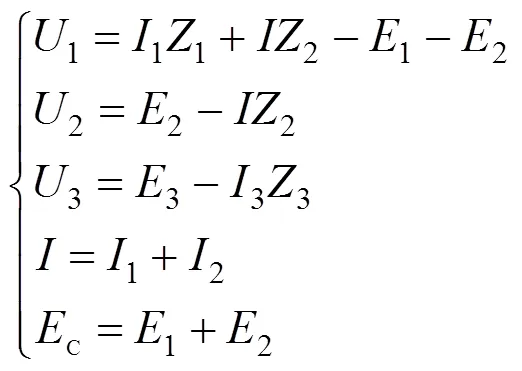
根据变压器的原理，自耦变压器中低压及中高压绕组之间的变比12和13分别为：

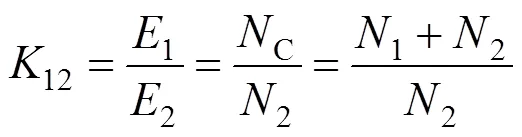
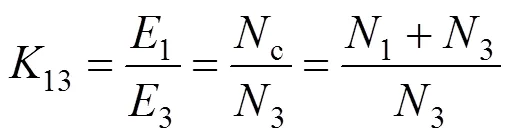
按照全电流定律，则磁势平衡关系有：

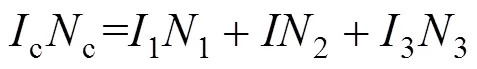
式(4)中为线圈圈数，将式(4)代入式(1)可得：

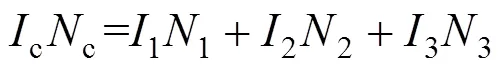
根据基尔霍夫电流定律，对式(5)进行等量变换，可得到下式：

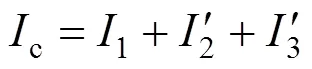
对式(1)~(7)进行等量代换，可得到下式：

通过对以上式子的分析，可以得到高速列车中单相三绕组自耦变压器的等效电路模型如图3所示(Z为励磁阻抗)。

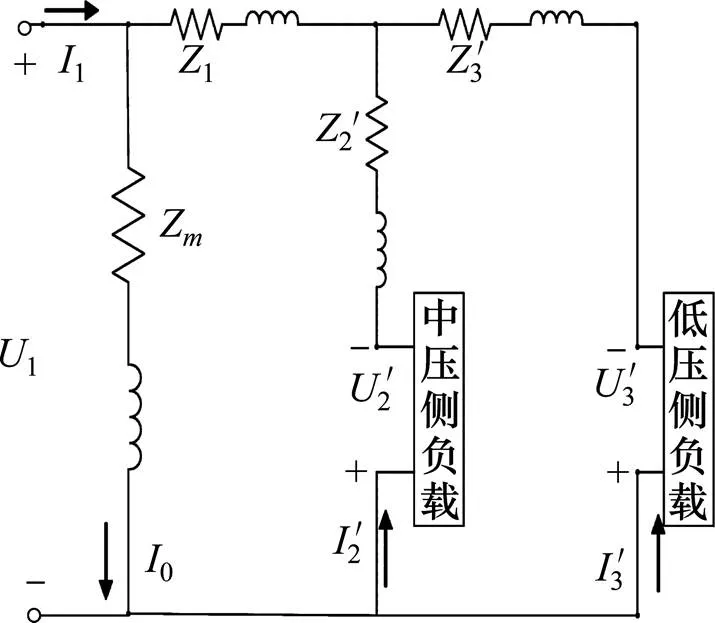
图3 自耦变压器等效电路模型

2.4 模型中各个参数的算法

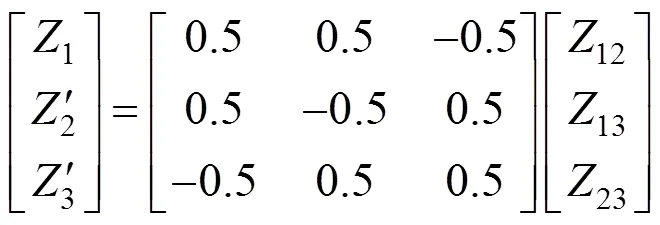
因此，在工程计算中，只需要知道12，13，23和C的值，可以利用图4的等效电路图，进行系统的潮流计算，得到各个参数的数值。但是在Matlab/Simulink仿真中，还需要知道高压侧、中压侧及低压侧绕组阻抗值大小。将式(8)~(9)联立求解，就可得到自耦变压器各绕组漏阻抗值的计算矩阵：

2.5 修正后的阻尼梯形法

在高速铁路供电系统中的自耦变压器，由于存在“励磁涌流”以及“漏抗”等现象，会在正常运行的某一段时间内产生谐波，这对列车的安全运行构成了极大的威胁。在仿真模型中仿真时，由于这些现象的存在，出现数值振荡，波形不规范，图像易失真。

考虑到自耦变压器高、中压绕组之间存在磁的联系，根据麦克斯韦理论，存在如下的一阶微分方程组：

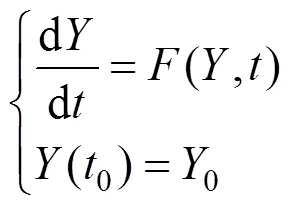
求解上面的方程组，通常采用欧拉法、后退欧拉法、隐式梯形法和龙格库塔法等[13]。由于本文所搭建的仿真模型，包含大量的非线性元件，运行时不可避免地会产生数值振荡，即非状态变量产生不正常的摆动。为了保持仿真过程中数值计算的稳定性和准确性以及图像的不失真，本文提出一种新型的阻尼梯形算法。为了便于讨论，考虑一阶常微分方程为：

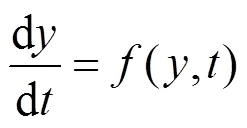
对式(12)的求解实质为对一组时间序列0，1，…，t按顺序求解出对应的状态量0，1，…，y。在[t,t+1]的时间段内写出式(12)的数值积分计算公式：

设计算步长=t+1−t，首先采用后退欧拉法对式(13)进行差分化：

然后，采用隐式梯形积分法对式(14)进行差 分化：

最后，将隐式梯形法和后退欧拉法按照(1−):的比例混合，形成阻尼梯形法差分公式：

式中：为阻尼因子，当=0时，上式转化为隐式梯形法；当=1时，上式转化为后退欧拉法；当0<<1时，上式转化为阻尼梯形法[17]。

对于模型中有关磁路的微分方程，均可以用式(17)来表示：

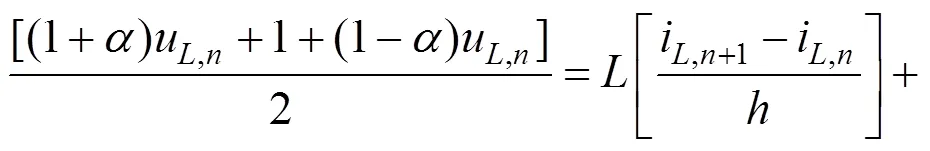
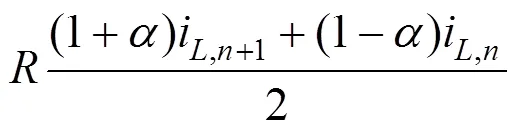
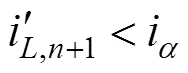
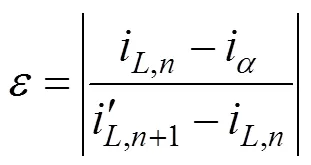
由式(19)可以得到式(17)校正后的公式为：

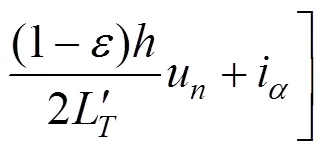
通过引入辅助因子，并不能完全杜绝数值振荡。因此，在仿真过程中，采用拟合函数对励磁电流i进行振荡补偿，拟合函数如下所示：

在仿真过程中，当=3−1时该算法具有稳定性，此时仿真误差具有更快的衰减速率，对数值振荡的抑制能力大大增强。

本文所提出的新型阻尼梯形算法，为了防止出现图像失真，抑制数值振荡，先对阻尼因子进行预测估值，再加入辅助阻尼因子进行校正，最后在仿真过程中对励磁电流i进行了振荡补偿。

3 自耦变压器模型搭建与仿真分析

本文以高速列车中的三相三绕组自耦变压器为研究对象，根据推导出的等效电路模型与数学模型，对自耦变压器的绕组进行参数计算。

3.1 绕组阻抗

根据自耦变压器参数及等效的数学模型，利用Matlab强大的矩阵处理功能，可计算出各绕组漏阻抗的标幺值，如表1所示。

表1 自耦变压器漏阻抗标幺值

3.2 Matlab/Simulink仿真模型

基于Simulink搭建的仿真平台，对于高速列车供电系统中的自耦变压器进行仿真，检测自耦变压器正常运行时所出现的谐波次数。

本文所搭建的自耦变压器模型参数严格按照我国高速铁路标准《TBT 2888—2010 电气化铁路自耦变压器》进行设置，并在AT输出端串联4台相位差7.5度的变压器，可输出24波形，使输出的波形易于观察谐波成分。

3.3 仿真结果分析

利用模型在Simulink中进行仿真时，采用新型的阻尼梯形算法消除了数值振荡问题，在仿真时选用Ode23tb算法，加入阻尼因子的预测及辅助阻尼因子校正，在误差允许的范围内进行振荡补偿，可以很好地解决刚性问题。

当自耦变压器在供电系统中正常运行时，其饱和磁滞回线如图4所示。

图4 自耦变压器器饱和磁滞回线

观察AT输入输出侧电压波形，输入侧电压波形如图5所示，输出侧电压波形如图6所示，从图中可以看出，当自耦变压器在正常运行过程中出现谐波时，输出侧的电压波形出现锯齿波，与正常出现的交流电压正弦波形明显不同，而且由于谐波的存在，使得自耦变压器2个输出侧出现短路，电压几乎为0，波动很小。

图5 输入侧电压波形

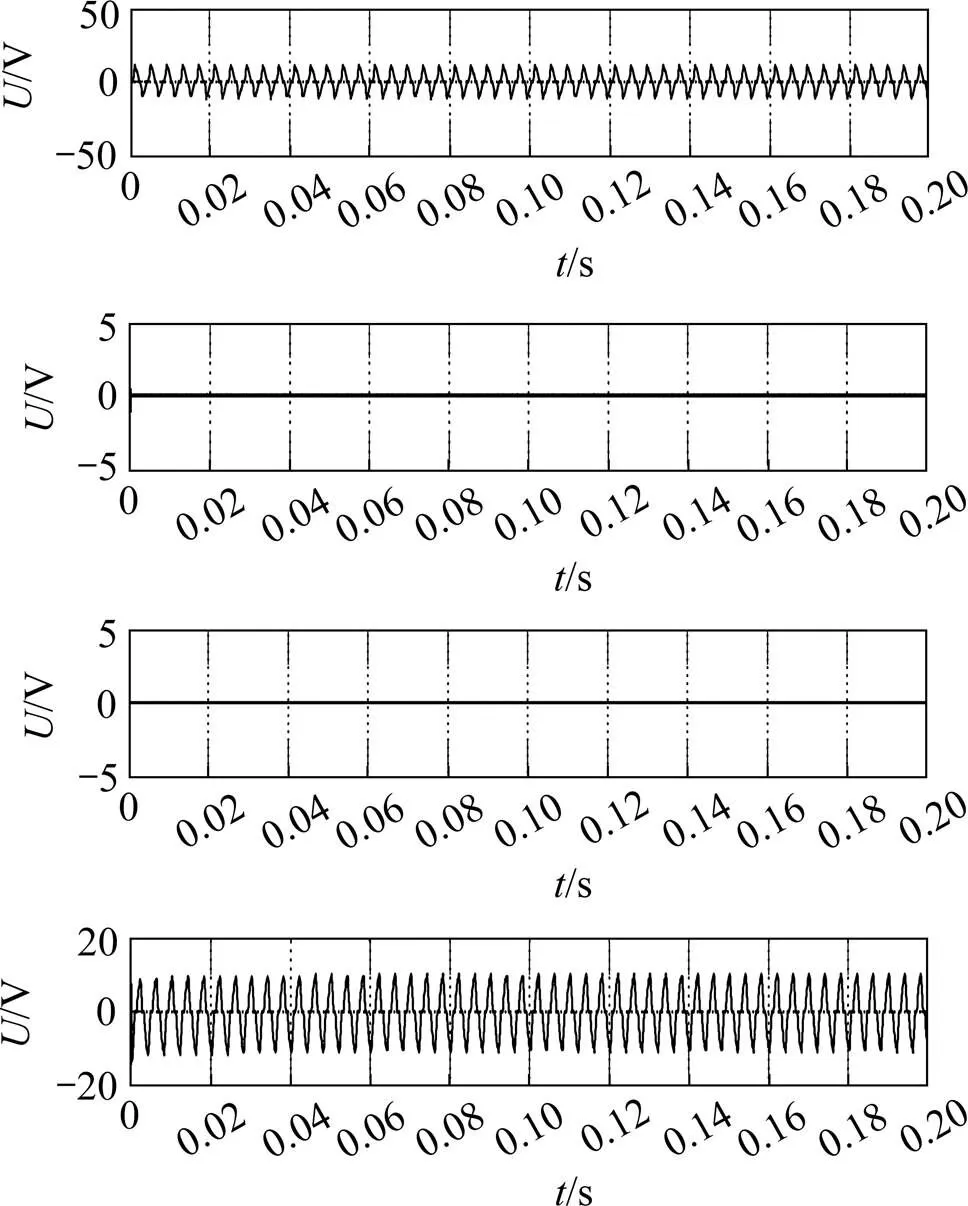
图6 输出侧电压波形

为了观测到谐波的次数，在自耦变压器的整流装置输出侧接入示波器，示波器波形如图7所示，由图7发现，自耦变压器在运行至=2 000 s左右时，出现15~18次的谐波，这也验证了在2009年9月份合武线合肥分区所长安集方向的列车在运行时从供电系统中检测到17和18次谐波，以及国内学者在2011年对大秦线大同市湖东牵引变电所进行实测时出现低频振荡，在2016年1月对徐州铁路枢纽进行频率测试时发现不同频率的髙次谐波。

图7 示波器波形

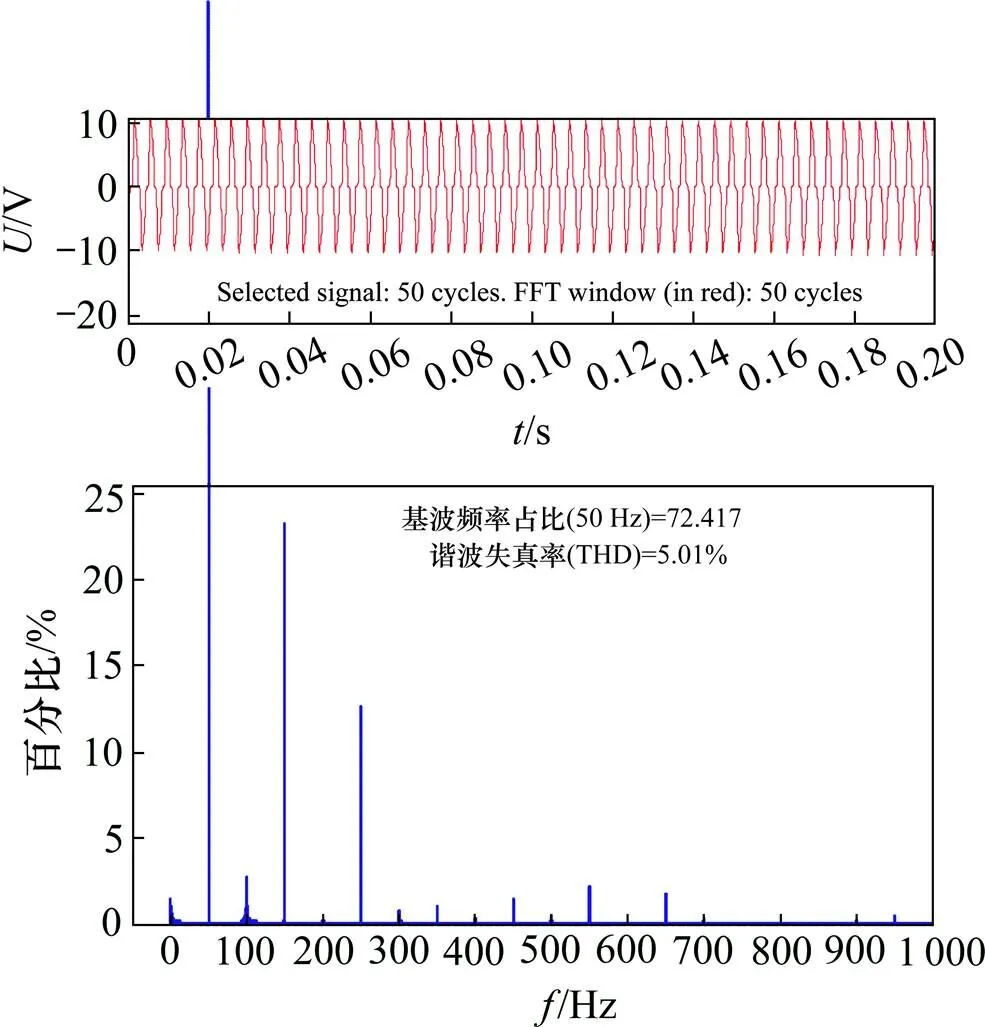
图8 谐波信号的FFT分析

对自耦变压器所出现的谐波波形进行进一步分析，在Simulink仿真中，采用电力图形用户分析界面(Powergui)模块，打开快速傅里叶变换(FFT)窗口，对自耦变压器中所出现得谐波波形进行分析，其波形如图8所示，发现图形中出现不规则的正弦波形，当出现髙次谐波时，总谐波失真率降至5.01%；在对信号的FFT分析结果图中，由于采用的是传统的Nuquist采样，对于频率远高于采样频率的信号，未能进行很好的采样，但是仍可以看出图中含有大量的髙次谐波。

对于Nuquist采样频率的缺陷，可以运用压缩感知(Compressive Sensing CS)理论来克服[15]，该理论以远低于Nuquist采样频率的速率来对髙次谐波频率进行采样压缩并恢复，本文由于篇幅原因，对压缩感知理论暂不进行讨论。

4 结论

1) 采用修正后的阻尼梯形算法以及将磁路与电路结合起来对自耦变压器进行建模，该模型不仅很好地解决了数值振荡问题，阻止图像失真，而且能对AT正常运行时的状态进行仿真。

2) 在AT模型仿真过程中，出现的谐波成分证明了在车网耦合振荡系统中自耦变压器所产生的谐波占据主要成分，并且当自耦变压器正常运行至=2 000 s时，系统检测到出现15~18次的高次谐波，之后频率又恢复正常，在整个过程中自耦变压器始终正常运行，谐波出现的时间也很短暂，与近几年来监测系统所监测到的现象相吻合，为抑制高次谐波的产生提供了数据支撑。

[1] 何洋阳, 黄康, 王涛, 等. 轨道交通牵引供电系统综述[J]. 铁道科学与工程学报, 2016, 13(2): 352−361. HE Yangyang, HUANG Kang, WANG Tao, et al. Overview of traction power supply system for rail transportation[J]. Journal of Railway Science and Engineering, 2016, 13(2): 352−361.

[2] 刘建强, 郑琼林, 杨其林. 高速列车牵引传动系统与牵引网谐振机理[J]. 电工技术学报, 2013, 28(4): 221−227. LIU Jianqiang, ZHENG Qionglin, YANG Qilin. Resonance mechanism between traction drive system of high-speed train and traction network[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 221−227.

[3] Hanmin L, Changmu Gilsoo J. Harmonic analysis of the Korean high-speed railway using the eight-port representation model[J]. IEEE Trans. on Power Delivery, 2006, 26(2): 979−986.

[4] 何正友, 胡海涛, 方雷, 等. 高速铁路牵引供电系统谐波及其传输特性研究[J]. 中国电机工程学报, 2011, 31(16): 55−62. HE Zhengyou, HU Haitao, FANG Lei, et al Research on the harmonic in high-speed railway traction power supply system and its transmission characteristic[J]. Proceedings of the CSEE, 2011, 31(16): 55−62.

[5] 张淇铭. 高铁牵引负荷的电网谐波分析[D]. 成都: 西南交通大学, 2015: 17−45. ZHANG Qiming. Analysis of power system harmonic generated by high-speed raid’s traction load[D]. Chengdu: Southwest Jiaotong University,2015: 17−45.

[6] 初曦. 高速列车与牵引网谐振现象及其抑制方法的研究[D]. 北京: 北京交通大学, 2014: 12−36. CHU Xi. Study on resonance and its supression between high-speed train and power supply line[D]. Beijing: Beijing Jiaotong University, 2014: 12−36.

[7] 徐晨博, 王丰华, 黄华, 等. 基于IEC 61850的变压器振动监测信息建模与实现[J]. 电力系统自动化, 2014, 38(4): 60−64. XU Chengbo, WANG Fenghua, HUANG Hua, et al. Information modeling and implementation of vibration on-line monitoring of power transformer based on IEC 61850[J]. Automation of Electric Power Systems,2014, 38(4): 60−64.

[8] Kritsada Mongkoldee, Thanatchai Kulworawanichpong. Current-based newton-raphson power flow calculation for AT-fed railway power supply systems[J]. International Journal of Electrical Power & Energy Systems, 2018, 98(6): 11−22.

[9] Worku G B , Kebede A B . Autotransformer fed traction power supply system: analysis, modeling and simulation[J]. 智能电网, 2018(2): 92−98.

[10] 高亚静, 苗宏佳, 吴文传, 等. 处理不接地配电网三相潮流不收敛的变压器建模新方法[J]. 电力系统自动化, 2014, 38(18): 53−57. GAO Yajing, MIAO Hongjia, WU Wenchuan, et al. A Novel transformer modeling method for overcoming divergence of three-phase power flow in ungrounded power distribution networks[J]. Automation of Electric Power Systems, 2014, 38(18): 53−57.

[11] 李勇, 王江峰, 何正友, 等. 高速铁路牵引供电系统动态模拟综合实验系统的设计与实现[J]. 电力系统保护与控制, 2014(13): 123−128. LI Yong, WANG Jiangfeng, HE Zhengyou, et al. Esign and implementation of integrated dynamic simulation experiment system of high-speed railway traction power supply system[J]. Power System Protection and Control, 2014(13): 123−128.

[12] 钱清泉, 高仕斌, 何正友, 等. 中国高速铁路牵引供电关键技术[J]. 中国工程科学, 2015, 17(4): 9−20. QIAN Qingquan, GAO Shibin, HE Zhengyou, et al. Study of China high-speed railway traction power supply key technology[J]. Chinese Engineering Science,2015, 17(4): 9−20.

[13] LIU J, WEI T, LIU J, et al. Suppression of numerical oscillations in power system electromagnetic transient simulation via 2S-DIRK method[C]// Power & Energy Engineering Conference, IEEE, 2016.

[14] 陈民武, 崔召华, 高鸿阁, 等. 基于双端电气量的高速铁路故障测距方法研究[J]. 铁道科学与工程学报, 2017, 14(10): 7−16. CHEN Minwu, CUI Zhaohua, GAO Hongge, et al. Study of fault location method of high-speed railway using two-terminal electrical quantities[J]. Journal of Railway Science and Engineering, 2017, 14(10): 7−16.

[15] Daniele C, Carlo M, Attilio P P, et al. Identification and estimation of harmonic sources based on compressive sensing[J]. IEEE Transactions on Instrumentation and Measurement, 2018: 1−10.

Modeling simulation and harmonic mechanism analysis of AT based on numerical oscillation elimination

DONG Weiguang1, XIN Guoqing1, GAO Fengyang1, LÜ Xiaoqiang2

(1. School of Electrical Engineering and Automation, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. State Grid Gansu Maintenance Company, Jiuquan 735000, China)

The theoretical analysis and simulation model of the autotransformer were built, but due to the magnetic coupling effect between the windings, the numerical oscillation occurs during the simulation and the image is distorted, and it has a new type of damping trapezoidal method to suppress the oscillation. Firstly, the damp factor alpha was predicted and estimated, then the auxiliary damp factor epsilon was added to correct, Finally, the excitation currentiwas compensated. The simulation results show that the constructed model can clearly reflect the harmonic waveforms appearing in the runtime of the autotransformer, and provide a reference basis for fault early warning when the harmonics are in the system.

high speed railway; autotransformer; numerical oscillation; damping ladder algorithm; simulation model; harmonic analysis

TM922.73

A

1672 − 7029(2019)09− 2324 − 07

10.19713/j.cnki.43−1423/u.2019.09.026

2018−12−26

国家重点研发计划项目(2017YFB1201003-020)

董唯光(1971−)，男，甘肃兰州人，副教授，博士，从事压缩感知在电气故障诊断中应用研究；E−mail：1833295171@qq.com

(编辑 阳丽霞)