基于上限分析原理的岩溶桩基破坏模式与极限承载力计算
汪婧
基于上限分析原理的岩溶桩基破坏模式与极限承载力计算
汪婧
(中铁十一局集团有限公司,湖北 武汉 430061)
针对下伏溶洞顶板极限承载力问题,提出等截面桩与阶梯型变截面桩的顶板极限承载力计算方法。基于极限上限法引入摩尔库伦准则,构建圆台状顶板破坏滑裂面,提出岩溶等截面桩的桩顶荷载与顶板厚度的关系式并分析式中参数对桩顶荷载与顶板厚度曲线的影响规律,同时结合算例对比数值解和解析算法的结果,论证该算法的可靠性。在此基础上,结合极限分析法推导阶梯型变截面桩各变阶处滑裂面的上限解,并寻找最先满足上限解的滑裂面,提出该溶洞顶板破坏模式并推导出桩顶荷载与顶板厚度的关系式,通过模型试验对比验证计算方法的有效性。该计算方法对于上述2类截面桩的极限承载力计算均较适用,对岩溶区桩基设计有一定参考价值。
岩溶桩基;极限上限定理;极限承载力;阶梯型变截面桩

随着我国西部大开发战略的实施,西部地区的交通事业快速发展。但西部部分地区地质地貌的特殊性,溶洞、采空区等特殊地质的存在给工程设计和施工带来了很大的影响。由于工程选址时不可能完全避开岩溶区,所以对岩溶的形成和承载力的研究显得十分必要[1−3]。极限分析理论最早由Fellenius等人在20世纪20年代提出,从50年代以来得到了较大的发展。近年来,部分学者将极限分析理论应用于下伏空洞的桩基承载力计算研究中,刘辉等[4]利用极限分析上限法推导出了圆形空洞上方条形基础的地基极限承载力解析公式。赵明华等[5]还利用上限有限元法计算出多种工况下的地基极限承载力上限解。雷勇等[6]引入格里菲斯非线性岩石强度准则,采用极限分析方法对顶板冲切破坏模式极限承载力计算方法进行了分析。目前对于岩溶桩基的承载稳定性问题研究主要以数值模拟[7]以及模型试验为主[8],理论解析方面的研究相对较少。基于格里菲斯准则的极限分析方法在进行岩溶桩基极限承载力的确定时主要考虑脆性完整岩石材料,但实际工程中的岩层并不完全发生脆性破坏,该准则存在一定的局限性,而且目前的研究对象主要以等截面桩为主,而针对阶梯型变截面桩的研究则少有涉及。随着岩溶地层阶梯型变截面桩应用的逐渐兴起[9],对其极限承载力的研究就显得极为重要。基于上述研究的不足,本文将极限分析法与摩尔−库伦屈服准则相结合,首先考虑岩溶地层等截面桩基破坏模式,对其桩基破坏问题进行上限分析,得到岩溶等截面桩的溶洞顶板破坏模式及顶板厚度的关系式。在此基础上,将该计算方法推广到阶梯型变截面桩的溶洞破坏模式的上限分析之中,从而得到岩溶阶梯型变截面桩的溶洞顶板破坏模式及顶板厚度的关系式。
1 等截面桩下伏溶洞顶板破坏模式上限分析
1.1 基于摩尔库伦准则的极限分析上限定理




将式(2)和(3)代入式(1)有:

由式(4)可以说明,在任意一个满足运动容许的速度场内,物体所处的真实荷载小于等于由虚功原理所解出的荷载。
1.2 岩溶顶板破坏模型
溶洞顶板破坏近似形成由圆台体母线发展的破坏面[10]。当溶洞较小时,顶板范围内滑裂面无法自由发展,破坏边界从桩端延伸至溶洞边界,如图1(a)。考虑下伏溶洞极为复杂且在地层中分布范围大,桩径往往会远小于溶洞大小,因此本文统一假定为相对桩径大得多的空溶洞,将模型进行简化,忽略溶洞边界对破坏的影响,简化成如图1(b)所示。

(a) 模型1;(b) 模型2
根据极限上限法假定破坏模式,并考虑对称性构建一种由刚性块体构成的破坏机制,考虑一简单均质溶洞顶板的岩溶桩基破坏模式,取对称的半桩进行分析,如图2(a)所示。桩端上部荷载为/2,桩端距溶洞顶板高度为,桩端下岩溶顶板临界滑裂面与竖直方向的夹角为,岩层内摩擦角为,黏聚力为,并做出以下假设:
1) 岩溶桩基顶板发生冲切破坏,分析属于平面问题;
2) 桩为嵌岩桩,桩端下方为均质岩体,且允许向下移动,破坏范围在溶洞顶板范围以内;
3) 岩层破坏服从Mohr-Coulomb屈服准则,且假定溶洞相对于桩径大得多,忽略溶洞边界对破坏的影响。

图2 极限平衡破坏模式和速度模式
如图2(a)所示,顶板破坏区分为2块,一块是桩端下方矩形岩层,跟随桩基一起沉降,另一块是滑裂面边三角形区域。将2块区域看做刚体,那么相互之间就会产生相对速度及塑性流动区。假定桩体的初速度为0,方向竖直向下,则桩端下方岩层速度也为0,1表示三角形区域岩层的向溶洞移动的速度,其相对速度可用0, 1表示,在相邻刚性块之间,存在着速度跃变线,表示跃变线与速度方向之间的夹角,几个速度之间的关系用矢量三角形表示,如图2(b)所示。
由速度矢量图可以得到1和0,1与桩端下岩溶顶板临界滑裂面与竖直方向的夹角,岩层内摩擦角为以及初速度0之间的关系:


1.3 岩溶顶板破坏模式
考虑溶洞顶板自重,外功率包括外部荷载/2所做的功率、矩形岩层以及靠近滑裂面三角形岩层重力所做的功率。
外部荷载/2所做的功率,为桩端上部荷载/2与初速度0的乘积:

岩层的外功率为其重力与沿重力方向的分速度的乘积,矩形岩层与靠近滑裂面三角形岩层产生的外功率分别为:



总的外功率为三者之和,其表达式如下:


内部损耗功率为2刚性块之间滑裂面的损耗功率,滑裂面上的能量损耗表示为:

滑裂面上的能量损耗可通过建立如图3所示的坐标系,并通过对进行积分得到:

其中()为的直线方程:

则总的内部损耗功率为滑裂面和上的能量损耗之和,表达式如下:

根据极限上限定理,外部功率等于内部损耗功率,即



对上式进行整理化简,可得上部荷载关于溶洞顶板厚度的目标函数:


当桩端的上部荷载远大于岩层重力时,可忽略岩层自重对溶洞顶板破坏的影响。在不考虑土的自重时,外功率只有外部荷载/2所做的功率,推理过程与考虑荷载的情况相似,此处不再赘述,其相应的目标函数为:

1.4 模型参数的影响分析
采用MATLAB软件编写相应的计算程序进行分析。选取岩溶区常见的石灰岩为研究基础,其岩层容重=25 kN/m3,泊松比=0.2,保持二者在研究参数过程中不变。图4为桩径对上部荷载与顶板厚度曲线的影响。保持研究参数和不变,改变桩径(分别取为1,2,3和4 m)。如图所示,相同溶洞顶板安全厚度的条件下,随着桩径的增大,承载能力增大,能承受的上部极限荷载也随之增大;相同的上部荷载的条件下,随着桩径的增大,承载能力也相应增大,所需要的溶洞顶板安全厚度随之减小。

图4 不同桩径下溶洞顶板安全厚度与上部极限荷载的关系曲线
图5为摩擦因数对上部荷载与顶板厚度曲线的影响。保持研究参数和不变,改变摩擦因数 (分别取为10°,20°,30°,40°和50°)。由图可知,相同溶洞顶板安全厚度的条件下,随着内摩擦角的增大,极限承载能力也随之提高;相同的上部荷载的条件下,随着内摩擦角的增大,所需要的溶洞顶板安全厚度随之减小。并且随着溶洞顶板安全厚度增大,上部荷载的极限值增加幅度也越高,内摩擦角越小其曲线的增幅趋势越平缓,可见,随着岩层的增大,破坏时的剪切破坏面也会随着增大,内摩擦角的抗破坏作用也会随之展现出来。

图5 不同内摩擦角下溶洞顶板安全厚度与上部极限荷载的关系曲线

图6 不同黏聚力下溶洞顶板安全厚度与上部极限荷载的关系曲线
图6为黏聚力对上部荷载与顶板厚度曲线的影响。保持研究参数和不变,改变黏聚力(分别取为10,20,30和40 MPa)。由图可知,相同溶洞顶板安全厚度的条件下,随着岩体的黏聚力的增大,承载能力增大,能承受的上部极限荷载也随之增大;相同的上部荷载的条件下,随着岩层的黏聚力的增大,承载能力也相应增大,所需要的溶洞顶板安全厚度随之减小。

表1 计算参数
1.5 算例验证
利用式(16)和(17)分别求出各对应溶洞顶板安全厚度下的上部荷载,同时引入文献[8]中的计算方法,计算围岩及桩体参数取值如表1所示。各对比曲线如图7所示。由图可见,溶洞顶板安全厚度在0~2 m范围内,本文采用的方法与文献[8]中的方法有较好的相似性。当增大时,与文献[8]方法之间就有了较为明显的偏差,相较于文献[8],由于考虑了嵌岩深度的因素,在较小时,相同厚度的溶洞顶板安全下,能够承受的上部荷载极限值会较大,而随着的增大,其计算结果却相较于其他几种方法较低,这是因为文献[8]中的安全系数考虑较高,安全储备预留较多。然而通过数值模拟的结果显示,本文的方法较为接近,相较于文献中的方法既不会偏于保守,也不会过分考虑溶洞边界对其的影响。

图7 不同计算方法的溶洞顶板安全厚度H与上部极限荷载P的关系曲线
2 阶梯型截面桩下伏溶洞顶板破坏模式上限分析
2.1 阶梯型截面桩下伏溶洞顶板的破坏模式
参考等截面岩溶桩基的溶洞顶板破坏模式,构建如图8所示的阶梯型变截面桩溶洞顶板破坏 模式。

图8 阶梯型变截面桩溶洞顶板潜在破坏模式
类比普通等截面桩在桩端桩周处发展滑裂面,假定存在3个潜在滑裂面Ⅰ,Ⅱ和Ⅲ,分别是从每级变阶边缘以及桩端边缘开始破坏并发展至溶洞顶板的临空面,则变截面空心桩的岩溶顶板破坏模式可能由滑裂面Ⅰ,Ⅱ和Ⅲ中其中1条构成。
根据式(18)可得到各滑裂面的上限分析方程,以滑裂面Ⅱ和Ⅲ为例:




为研究阶梯型变截面桩最有可能的溶洞顶板滑裂面,将式(19)和(20)相除,得





则将式(20)改写为


同理可以获得任意2滑裂面上限解的比值,根据实际工程中的相应位置的上部荷载比值来推断先发生破坏的滑裂面,最终寻找出最先发生破坏的滑裂面,即为阶梯型变截面桩溶洞顶板的破坏 模式。
2.2 阶梯型变截面桩下伏溶洞顶板破坏模型
当阶梯型变截面空心桩的岩溶顶板破坏发生在桩端底面,最后一阶的底端,即可构建如图9所示的破坏模式,虚线表示溶洞顶板因上部荷载产生的滑裂面,计算假定同等截面桩。

图9 阶梯型变截面溶洞顶板破坏模式
根据极限上限法假定破坏模式,取对称的半桩进行分析,如图10(a)所示。桩端上部荷载为/2,桩端距溶洞顶板高度为,桩端下岩溶顶板临界滑裂面与竖直方向的夹角为,土体内摩擦角为,黏聚力为。
由于存在变阶面的关系,部分荷载从变阶处传递到周边土体,实际引起溶洞顶板破坏的荷载为传至桩端的竖向荷载。结合如图10(b)所示的速度矢量分析图,通过极限上限定理,使得外部功率等于内部损耗功率,可得
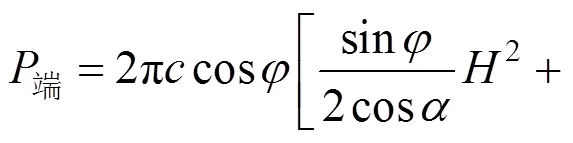

2.3 桩端荷载的计算方法

从而桩端荷载可表示为:


图10 极限平衡破坏模式与速度模式

图11 2次变截面桩计算模型图
图11所示为2次阶梯型变截面桩的细部尺寸图,则根据桩基极限承载力的计算公式,桩侧摩阻力可表示为:


其中:q为桩侧土层的极限侧阻力标准值。
变阶处阻力可表示为:


其中:q极限端阻力标准值。
2.4 n阶变截面桩P(H)函数构建
通过上述推导,将其推广到阶变截面桩的情况,如图12所示,由于变截面桩的特殊性和下伏溶洞地层的影响下,桩周土体会存在松动现象,无法完全发挥极限侧摩阻力及变阶处端阻力,因此引入折减系数1和2,其值可由数值模拟或模型试验确定。
根据上述的推导过程,桩侧摩阻力和变阶处阻力可表示为:

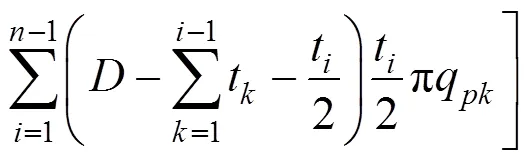

图12 n阶变截面桩计算模型图
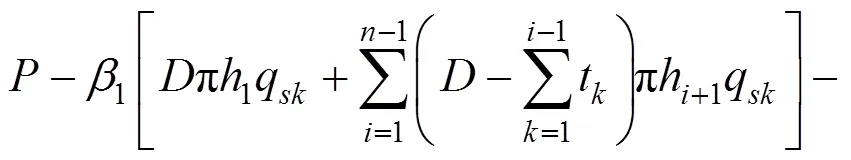

2.5 算例验证
针对阶梯型变截面桩的溶洞顶板破坏模式的研究,开展了多组模型试验,将试验桩的几何参数及试验参数代入式(32)进行极限荷载的计算。图13为试验结果与理论计算曲线。由图中曲线可知,理论与试验结果较为相近,总体趋势较为吻合。

图13 试验结果与理论计算对比曲线
3 结论
1) 针对基于极限上限法推导的上部荷载关于溶洞顶板厚度的目标函数进行参数分析,溶洞岩层黏聚力,内摩擦角和桩的直径对上部极限荷载均为正相关,有利于提高岩溶桩基的极限承载力。
2) 本文提出的方法所需参数较少,并且忽略溶洞边界对破坏的影响,提供了一定的安全储备,对工程设计有很大的便利之处,能对初步设计提供较好的参考。
3) 通过对岩溶等截面桩基溶洞顶板破坏的研究分析,类比推理阶梯型变截面空心桩溶洞顶板潜在滑裂面,提出以桩端处延伸至溶洞的阶梯型变截面桩的溶洞顶板破坏模式,并得到了岩溶等截面桩以及阶梯型截面桩的顶板极限承载力计算方法。
[1] Waltham A C, Swift G M. Bearing capacity of rock over mined cavities in Nottingham[J]. Engineering Geology, 2004, 75(1):15−31.
[2] Hatzor Y H, Wainshtein I, Mazor D B. Stability of shallow karstic caverns in blocky rock masses[J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47(8):1289−1303.
[3] JIANG C, LIU L, WU J P. A new method determining safe thickness of karst cave roof under pile tip[J]. Journal of Central South University, 2014, 21(3):1190−1196.
[4] 刘辉, 杨峰, 阳军生. 空洞上方浅基础地基破坏模式与极限承载力分析[J]. 岩土力学, 2010, 31(11): 3373− 3378.LIU Hui, YANG Feng, YANG Junsheng. Failure mechanism and ultimate bearing capacity of strip footing above void[J]. Rock and Soil Mechanics, 2010, 31(11): 3373−3378.
[5] 赵明华, 卢晓明, 张锐. 下伏空洞地基极限承载力与破坏模式上限有限元法[J]. 岩土力学, 2017, 38(1): 229−236, 246.ZHAO Minghua, LU Xingming, ZHANG Rui. Upper bound finite element method for ultimate bearing capacity and failure mechanism of subgrade above void[J]. Rock and Soil Mechanics, 2017, 38(1): 229−236, 246.
[6] 雷勇, 尹君凡, 陈秋南, 等. 基于极限分析法的溶洞顶板极限承载力研究[J]. 岩土力学, 2017, 38(7): 1926− 1932.LEI Yong, YIN Junfan, CHEN Qiunan, et al. Study on the ultimate bearing capacity of karst roof based on limit analysis[J]. Geotechnical Mechanics, 2013, 38(7): 1926− 1932.
[7] 王华牢, 张鹏, 李宁. 岩溶洞穴对嵌岩单桩承载力的影响研究[J]. 西安理工大学学报, 2010, 26(1): 31−36.WANG Hualao, ZHANG Peng, LI Ning. Research on the single rock-socketed pile bearing capacity influenced by karst caves[J]. Journal of Xi’an University of Technology, 2010, 26(1): 31−36.
[8] 黄明, 付俊杰, 陈福全, 等. 桩端岩溶顶板的破坏特征试验与理论计算模型研究[J]. 工程力学, 2018, 35(10): 172−182.HUANG Ming, FU Junjie, CHEN Fuquan, et al. Theoretical calculation model and model test on the failure characteristic of karst roof under rock-socketed pile[J]. Rock and Soil Mechanics, 2018, 35(10): 172− 182.
[9] 黄明, 江松, 许德祥, 等. 超大直径变截面空心桩的荷载传递特征与理论模型[J]. 岩石力学与工程学报, 2018, 37(10): 2370−2383.HUANG Ming, JIANG Song, XU Dexiang, et al. Load transfer mechanism and theoretical model of step tapered hollow pile with huge diameter[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(10): 2370− 2383.
[10] 雷勇, 刘一新, 邓加政, 等. 冲切破坏模式下溶洞顶板极限承载力计算[J]. 岩石力学与工程学报, 2018, 37(9): 2162−2169. LEI Yong, LIU Yixin, DENG Jiazheng, et al. Calculation of ultimate bearing capacity of cave roof under punching failure mode[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(9): 2162−2169.
Failure mode and ultimate bearing capacity of karst pile foundation based on upper-bound theorem
WANG Jing
(China Railway 11 Bureau Group Co. Ltd., Wuhan 430061, China)
In view of the problem of the ultimate bearing capacity of the roof of the underlying karst cave, the calculation method of the ultimate bearing capacity of the roof of the equal section pile and the stepped variable section pile was put forward. Mohr coulomb criterion, introduced based on the upper-bound theorem, build the frustum of a cone shaped roof damage critical slip surface, put forward such as karst section pile top load and the relation between the thickness of roof and analytical parameters on pile top load and the influence law of roof thickness curve, at the same time, combined with the numerical solution of examples and the result of the parsing algorithm, proved the reliability of the algorithm. On this basis, combined with the limit analysis method, the upper limit solution of sliding surface at each variable order of stepped type variable section pile was deduced, and the first sliding surface that meets the upper limit solution was found, the failure mode of roof of karst cave was put forward, and the relationship between pile top load and roof thickness was derived. The calculation method was suitable for the calculation of the ultimate bearing capacity of the above two kinds of cross-section piles and has certain reference value for the design of karst area pile foundation.
karst pile foundation; upper-bound theorem; ultimate bearing capacity; stepped variable section pile
TU473
A
1672 − 7029(2019)09− 2207 − 08
10.19713/j.cnki.43−1423/u.2019.09.011
2018−11−14
国家重点研发计划项目(2018YFC0808704)
汪婧(1982−),女,江西景德镇人,高级工程师,从事工程技术与管理相关工作;E−mail:8295161@qq.com
(编辑 涂鹏)

