考虑同球向双球面支座阻尼间隙的简支梁桥减隔震性能分析
于伟栋,张永亮,吴延伟,王希慧
考虑同球向双球面支座阻尼间隙的简支梁桥减隔震性能分析
于伟栋1,张永亮1,吴延伟2,王希慧3
(1. 兰州交通大学 土木工程学院,甘肃 兰州 730070;2. 中铁第一勘察设计院集团有限公司,陕西 西安 710043;3. 衡水宝力工程橡胶有限公司,河北 衡水 053000)
为研究同球向双球面纵向活动支座阻尼间隙对高速铁路简支梁桥地震响应的影响,综合考虑支座摩擦及减震榫阻尼器非线性,提出同球向双球面支座的有限元模拟方法,进行罕遇地震作用下顺桥向动力时程分析。研究结果表明:基于同球向双球面支座的简支梁桥减隔震体系具有隔断地震荷载和减小墩梁相对位移的双重控制作用;适当减小活动支座阻尼间隙可在保证墩底弯矩不显著增加的前提下大幅减小墩梁相对位移量;适当调整活动支座阻尼间隙的大小既可以对活动支座本身各部件之间的耗能量关系进行重分配,也可以优化固定支座和活动支座之间的耗能关系;活动支座耗能能力随其阻尼间隙的增大而降低。
高速铁路;简支梁桥;同球向双球面支座;地震反应;纵向活动支座阻尼间隙

我国是地震多发的国家,地震活动有频率高、强度大、震源浅和分布广的特点。特别是近几年,我国西南部地震频发。桥梁作为生命线工程,在抗震救灾中起着至关重要的作用。相对于单纯依靠结构强度抵抗地震的传统抗震体系,减隔震体系有抗震效果明显、经济成本低并且更能体现基于性能的抗震设计理念[1]。减隔震支座是目前减隔震技术应用于实际工程的具体体现,按体系可分为橡胶类隔震体系、滑动摩擦体系和弹塑性钢耗能体系。随着减隔震支座的大量应用,国内外学者开展了大量研究。LIU等[2−3]探讨了一种由橡胶柱心与低屈服点钢耗能器组成的新型减隔震支座应用于铁路简支梁桥的减隔震性能,并进行了试验和数值模拟分析。结果显示,文中钢阻尼器能够在保证支座变形可控的同时有效减小墩顶位移和墩底内力地震响应。Providakis等[4]通过数值分析方法证明经过适当设计的钢阻尼器能够在不明显增大地震响应的同时减小墩、梁相对位移。夏修身等[5]分析了墩高、地震强度及场地类型变化对采用摩擦摆支座的简支梁桥地震反应的影响。徐艳红等[6−8]都通过试验和有限元软件分别证明了2种不同外形的钢阻尼器具有稳定的滞回性能和良好的塑性变形能力。李爱丽等[9]通过试验说明减震榫可以同时满足桥梁在正常使用阶段的水平刚度要求和地震作用下的耗能要求。上述研究大多都是通过试验及有限元分析方法探讨减震榫的抗震性能或其他类型减隔震支座对桥梁地震响应的影响。但减震榫大多作为独立外设阻尼装置,基于“功能分离”的概念将其与其他减隔震支座配合使用;少有将减震榫耗能器与摩擦摆高度集成于同一支座系统的减隔震装置。为探讨同球向双球面减隔震支座的减隔震性能,本文以高速铁路简支梁桥为研究对象,利用时程分析方法系统分析了纵向活动支座阻尼间隙[10]对同球向双球面支座减隔震性能的影响。
1 同球向双球面支座构造及其减隔震机理
1.1 同球向双球面支座结构
同球向双球面支座按照功能可以分为4类,即固定支座、纵向活动支座、横桥向活动支座和多向活动支座[13]。支座主要包括:球形钢支座本体、减震榫耗能器和剪力销。减震榫将上支座板和下摆座相连接,减震榫顶部在上支座板的上孔内,减震榫的底部固定下摆座的下孔内。减震榫的顶部为球台状,当支座为固定式时,减震榫与上支座板固定;当支座为单向活动式时,上支座板留有上孔,为长槽形,同时,上摆设置有导轨,上支座板的底面设置有与导轨相匹配的滑槽,这样满足温度、徐变等引起的上部结构变形需求;减震榫的中部为锥台状,稳固性好;减震榫的底部为圆柱状,减震榫的底部外径与下孔内径相匹配,使减震榫的底部与下孔连接紧密。剪力销连接中间摆与下摆座。以纵向活动支座为例,支座结构见图1。
1.2 同球向双球面支座工作机理
同球向双球面支座采用正常使用功能与减、隔震功能分离的设计思路,同时具备普通球形支座与减隔震支座的2种功能,能满足高速列车正常使用条件下各项要求,其工作机理可分为2个阶段:
1) 正常使用及多遇地震作用下:以2球面间的相互转动适应梁的转动变形,由剪力销承担桥梁的水平荷载。支座结构处于弹性工作状态,满足承载力要求,并利用活动支座的阻尼间隙适应因温度、徐变等引起的上部结构变形。

1—上支座板;2—导向滑板;3—平面不锈钢板;4—平面改性聚四氟乙烯板;5—上摆;6—球面不锈钢板;7—球面改性聚四氟乙烯板;8—中间摆;9—高吸能耐磨滑板;10—下摆座;11—挡圈;12—剪力销;13—耗能器;14—锚栓
2) 罕遇地震作用下:剪力销被剪断,上支座板与下摆座产生相对滑移,隔断地震荷载,减震榫受力产生变形,同时支座利用摩擦作用与减震榫塑性耗能作用消耗地震能量。
2 工程概况
某4×32 m高速铁路简支梁桥的立面布置见图2,主梁采用等截面单箱单室箱梁,桥墩采用圆端形重力式桥墩,墩高13 m。每跨的梁体质量为1 225.7 t(含二期恒载)。Midas civil软件建立的三维有限元模型见图3,其中梁、墩及承台都采用空间梁单元建模,地基土对结构的约束作用简化成转动弹簧及平动弹簧施加在承台底,弹簧刚度取值采用m法计算。根据文献[11−12],墩高接近的多跨简支梁,轨道系统纵向约束对桥梁的地震反应影响较小,为简化计算模型,本文忽略了轨道约束的影响。

单位:cm
安评报告提供了3条罕遇地震加速度时程曲线,地震波峰值加速度为0.31,Ⅱ类场地,场地特征周期g=0.35 s。图4给出了其中一条安评地 震波。

图3 三维有限元模型

图4 罕遇地震加速度时程
3 分析模型
3.1 同球向双球面支座系统力学模型
同球向双球面支座力学模型的建立主要考虑了支座中减震榫耗能器塑性耗能作用、支座摩擦作用以及纵向活动支座中阻尼间隙的影响。使用Midas分析时,同球向双球面支座的恢复力模型为特殊的多折线弹塑性模型,支座具体模拟方法分别见图5和图6。
1) 减震榫耗能器的滞回模型采用双线性模型模拟[7],见图5(a)和图6(a)。
2) 利用双线性模型模拟支座中间摆与下摆座之间的曲面摩擦作用,见图5(b)和图6(b);利用理想弹塑性模型模拟支座上支座板与上摆之间的平面摩擦作用,见图6(c)。
3) 纵向活动支座导轨与滑槽之间预留的阻尼间隙采用间隙单元限制单元的正向位移,采用钩单元限制单元的负向位移[14−16]。其中当单元正、负向位移达到最大值后,间隙单元与钩单元刚度为无穷大,即不考虑支座导轨与滑槽的变形影响。
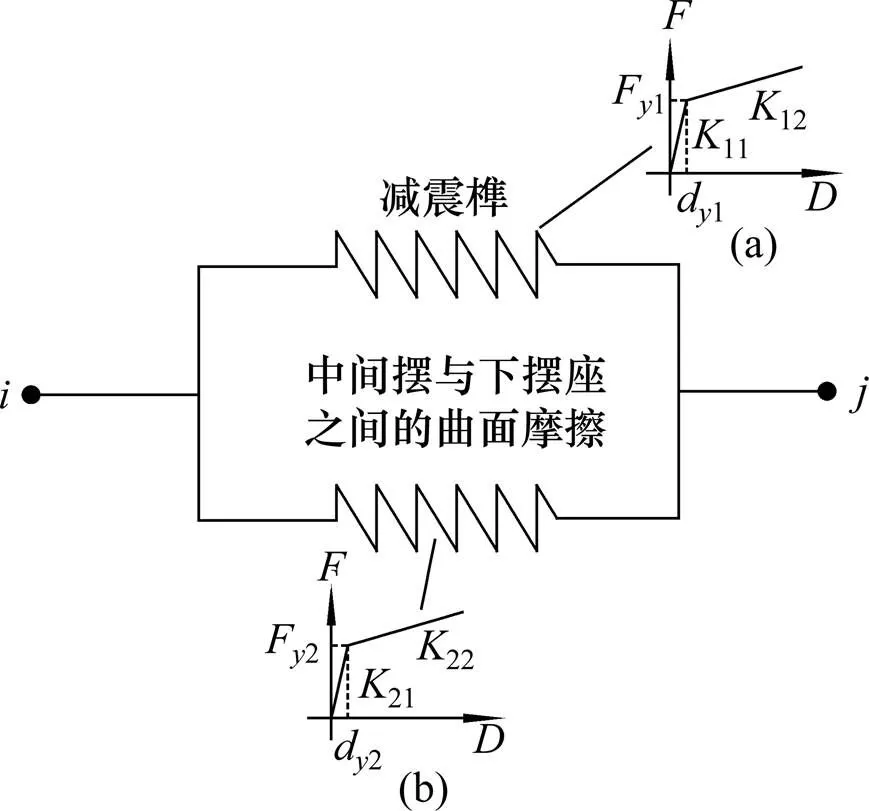
图5 固定式同球向双球面支座模拟

图6 纵向活动同球向双球面支座模拟
图6中,01为纵向活动支座上支座板与上摆之间平面摩擦作用可正向活动的范围,02为其可负向活动的范围,一般情况下设置01=02,即平面摩擦作用可活动的范围−02~01。11为减震榫初始刚度,12为减震榫屈服后刚度,F1,d1分别为减震榫的屈服力与屈服位移。21为中间摆与下摆座曲面发生相对滑动前刚度,22为其相对滑动后刚度,F2,d2分别为曲面摩擦作用的屈服力与屈服位移。31为上支座板与上摆平面发生相对滑动前刚度,32为其相对滑动后刚度。
限制正向位移的间隙单元的非线性力——变形关系为:

限制负向位移的钩单元的非线性力——变形关系为:
式中:d为梁体位移;d为墩顶位移,位移以向右为正,向左为负。01与02均为正值。
综上所述,将减震榫模型与曲面摩擦模型并联可得到固定式同球向双球面支座系统模型;将减震榫模型与曲面摩擦模型并联,同时将平面摩擦模型与活动支座阻尼间隙模型并联,最后将上述2个并联模型串联可得到纵向活动同球向双球面支座系统模型。
3.2 有限元抗震模型设置
为对比高速铁路简支梁桥传统抗震体系与采用同球向双球面减隔震支座的简支梁桥减隔震体系在罕遇地震作用下顺桥向地震响应,设置了3种分析模型(见图7),各抗震模型中支座参数见表1。抗震模型具体设置如下:
模型1 (传统抗震体系):固定支座与活动支座都采用普通支座,固定支座通过墩、梁竖向与顺桥向平移自由度耦合的方式模拟,其他自由度均相互独立;活动支座通过墩、梁竖向自由度耦合的方式模拟,其他自由度均相互独立。不考虑活动支座的平动摩擦作用。
模型2:固定支座采用固定式同球向双球面支座,活动支座采用普通支座。考虑活动支座的平动摩擦作用(平动摩擦因数采用0.03)。
模型3:固定与活动支座都采用同球向双球面支座。考虑活动式同球向双球面支座的阻尼间隙、上支座板与上摆之间活动范围受限的平面摩擦作用以及中间摆与下摆座的曲面摩擦作用。
其中模型1为对照组,通过模型2和模型3的对比分析来探讨基于同球向双球面支座的简支梁桥减隔震体系抗震性能。
然后,以模型3为研究平台,利用时程分析方法通过设置不同的纵向活动式同球向双球面支座阻尼间隙说明其对减隔震效果的影响。

(a) 模型1;(b) 模型2;(c) 模型3

表1 同球向双球面减隔震支座设计参数
4 有限元分析
4.1 3种减隔震体系对比分析
为对比分析简支梁桥传统抗震体系与基于同球向双球面支座的减隔震体系的罕遇地震响应。以3号墩地震响应为例,表2给出了3种模型在3条安评地震波作用下的地震响应平均值,图8和图9分别给出了阻尼间隙为10 mm时1条地震波作用下3种抗震体系模型的墩底弯矩和支座变形对比结果。其中支座变形结果也代表着墩梁相对位移的程度。
由表2、图8和图9可知:1) 基于同球向双球面支座的简支梁桥减隔震设计能有效降低地震墩底弯矩响应,模型2与模型3的墩底弯矩减震率平均值分别为69%和64%。2) 模型3最大墩梁相对位移较模型2减小了约40%,这说明设置有减震榫耗能器和高吸能耗能滑板的同球向双球面减隔震活动支座能更加有效地限制墩梁相对位移,在很大程度上减小了桥梁在震后发生落梁破坏的可能性。

表2 模型地震响应

图8 墩底弯矩时程
综上所述,合理配合使用固定和纵向活动同球向双球面减隔震支座进行简支梁桥减隔震设计可以实现隔断地震荷载和减小墩梁相对位移双重控制作用。

图9 纵向活动支座变形时程
4.2 活动支座阻尼间隙对其减隔震效果的影响
为探究同球向双球面减隔震活动支座阻尼间隙大小对简支梁桥减隔震效果的影响。图10和图11分别给出了模型3中3号墩墩底弯矩与活动支座变形随活动支座阻尼间隙变化的变化情况。

图10 3号墩墩底弯矩

图11 3号墩活动支座变形
图12和图13给出了同球向双球面减隔震固定与活动支座中减震榫的榫顶最大水平变形量随活动支座阻尼间隙变化的变化规律。
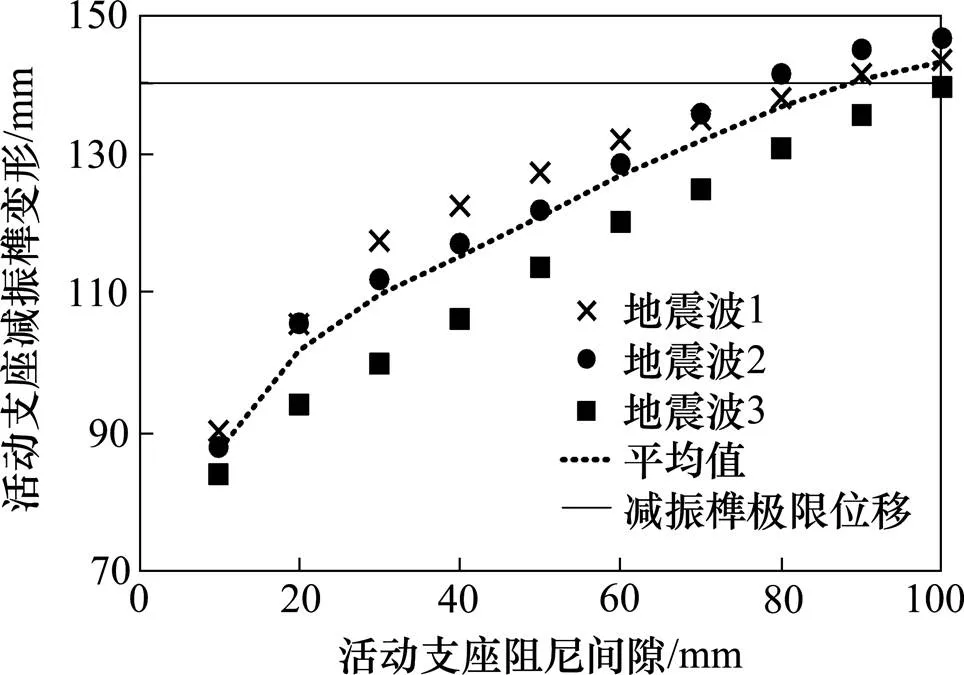
图12 3号墩固定支座减震榫耗能器变形

图13 3号墩活动支座减震榫耗能器变形
由图10~13可知:1) 墩底弯矩在不同地震波作用下有明显的离散现象,这与以前的桥梁减隔震研究结论一致。2) 墩梁相对位移随着支座阻尼间隙的增加逐渐增大。3) 随着活动支座阻尼间隙的增加,固定和活动支座减震榫最大变形值变化趋势恰好相反,其中固定支座中减震榫最大变形值逐渐增大。
考虑图12中,当活动式同球向双球面支座阻尼间隙超过80 mm后,减震榫榫顶水平变形量将超过其最大允许变形量。图14仅给出了减隔震活动支座阻尼间隙从10 mm到70 mm变化过程中3号墩顶支座在3条地震波作用下累计耗能量平均值统计。

(a) 固定支座;(b) 活动支座
由图14可以看出阻尼间隙从10 mm增加到70 mm的过程中:1)随着减隔震活动支座阻尼间隙的增加,减隔震固定支座累计耗能量逐渐增加;而减隔震活动支座累计耗能量逐渐减小。2) 减隔震活动支座中减震榫累计耗能量和中间摆与下摆座曲面摩擦累计耗能量都随活动支座阻尼间隙的增加有逐渐减少的趋势。3) 上支座板与上摆的平面摩擦累计耗能量随着活动支座阻尼间隙的增加逐渐增加。4) 当活动支座阻尼间隙较小时,活动支座耗能作用主要依赖于中间摆与下摆座曲面摩擦作用和减震榫塑性变形耗能作用;当阻尼间隙较大时,活动支座耗能作用主要依赖于上支座板与上摆的平面摩擦作用。
为定量衡量活动支座阻尼间隙变化对支座系统耗能能力的影响,图15给出了支座等效黏滞阻尼系数[17]随阻尼间隙的变化情况。

图15 活动支座等效黏滞阻尼系数
从图15可以得到:同球向双球面活动支座随其阻尼间隙的增加,其耗能能力出现显著降低;在支座阻尼间隙从10 mm逐渐增加到70 mm的过程中,模型3在3条地震波作用下,活动支座的等效黏滞阻尼系数平均降低了约27%。
5 结论
1) 基于同球向双球面支座的简支梁桥减隔震体系具有隔断地震荷载和减小墩梁相对位移的双重控制作用。
2) 纵向活动支座阻尼间隙的变化对墩底弯矩影响不大,但阻尼间隙的增加会导致墩梁相对位移的明显增大。
3) 适当调整活动支座阻尼间隙可以减小固定支座的耗能压力,优化减隔震体系中固定支座和活动支座的耗能关系;当活动支座阻尼间隙较小时,活动支座耗能作用主要依赖于中间摆与下摆座曲面摩擦作用和减震榫塑性变形耗能作用;当阻尼间隙较大时,活动支座耗能作用主要依赖于上支座板与上摆的平面摩擦作用;活动支座耗能能力随其阻尼间隙的增大而降低。
本次研究还存在以下不足之处:仅针对采用同球向双球面减隔震支座的桥梁减隔震体系剪力销剪断之后的阶段做了相应分析,并未对从地震刚发生到地震结束的全过程进行地震响应分析。
[1] Bertero R D, Bertero V V. Performance-based seismic engineering: The need for a reliable conceptual comprehensive approach[J]. Earthquake Engineering Structure Dynamics, 2002, 31(3): 627−52.
[2] LIU Cong, GAO Ri, GUO Bo. Seismic design method analyses of an innovative steel damping bearing for railway bridges[J]. Engineering Structures, 2018, 167: 518−532.
[3] LIU C, GAO R, LEI J Q. Shaking table tests of an innovative steel damping bearing for railway bridges[C]// In: International bridge conference, Maryland, 2018.
[4] Providakis C P. Effect of supplemental damping on LRB and FPS seismic isolators under near-fault ground motions[J]. Soil Dynamics Earthquake Engineering, 2009, 20(1): 80−90.
[5] 夏修身, 赵会东, 欧阳辉来. 高速铁路桥梁基于摩擦摆支座的减隔震研究[J]. 工程抗震与加固改造, 2014, 36(3): 21−26. XIA Xiushen, ZHAO Huidong, OUYANG Huilai. Study on seismic isolation of high speed railway bridge with friction pendulum bearings[J]. Earthquake Resistant Engineering and Retrofitting, 2014, 36(3): 21−26.
[6] 徐艳红, 李爱群, 黄镇. 抛物线外形软钢阻尼器试验研究[J]. 建筑结构学报, 2011, 32(12): 202−209. XU Yanhong, LI Aiqun, HUANG Zhen. Experimental study of mild steel dampers with parabolic shape[J]. Journal of Building Structures, 2011, 32(12): 202−209.
[7] 孟兮, 倪燕平. 减震榫设计及试验研究[J]. 北京交通大学学报, 2013, 37(3): 103−106. MENG Xi, NI Yanping. Design and experimental study of shock absorber[J]. Journal of Beijing Jiaotong University, 2013, 37(3): 103−106.
[8] 孟兮, 高日, 李承根. 减震榫滞回性能理论及试验研究[J]. 桥梁建设, 2015, 45(3): 20−25. MENG Xi, GAO Ri, LI Chenggen. Theoretical and experimental study of hysteretic behavior of shock absorber[J]. Bridge Construction, 2015, 45(3): 20−25.
[9] 李爱丽, 高日, 李承根, 等. 一种新型软钢减震榫的设计与试验研究[J]. 桥梁建设, 2017, 47(1): 23−28. LI Aili, GAO Ri, LI Chenggen, et al. Design and experimental study of a novel type of mild steel shock absorber[J]. Bridge Construction, 2017, 47(1): 23−28.
[10] 魏标, 杨添涵, 蒋丽忠. 轨道结构建模精细化程度对高速铁路连续梁桥地震易损性的影响[J]. 工程力学, 2018, 35(4): 16−23. WEI Biao, YANG Tianhan, JIANG Lizhong. The effects of model refinement of ballastless tracks on the seismic vulnerability of a continuous bridge on a high-speed railway[J]. Engineering Mechanics, 2018, 35(4): 16−23.
[11] 张永亮, 陈兴冲, 李子奇. 轨道约束系统对高速铁路多跨简支梁桥地震反应的影响[J]. 世界地震工程, 2010, 26(4): 6−12. ZHANG Yongliang, CHEN Xingchong, LI Ziqi. Effects of rail system restraints on seismic response of multi-span simply supported girder bridge on high-speed railway[J]. World Earthquake Engineering, 2010, 26(4): 6−12.
[12] JT/T 843—2012, 公路桥梁弹塑性钢减震支座[S]. JT/T 843—2012, Elastic-plastic steel damping bearings for highway bridges[S].
[13] T/TMAC 001—2017, 同球向双球面减隔震支座[S]. T/TMAC 001—2017, The same spherical direction double spherical surface seismic mitigation and isolation bearing[S].
[14] 王常峰, 陈兴冲, 朱春林, 等. 考虑支座及限位装置非线性的接触摩擦单元模型[J]. 工程力学, 2013, 30(8): 186−192. WANG Changfeng, CHEN Xingchong, ZHU Chunlin, et al. The contact-and-friction element considering nonlinear performance of movable supports and resrainers[J]. Engineering Mechanics, 2013, 30(8): 186− 192.
[15] 王常峰, 包仪军, 陈兴冲, 等. 活动支座状态对桥梁弹塑性地震反应的影响[J]. 公路交通科技, 2015, 32(3): 75−81. WANG Changfeng, BAO Yijun, CHEN Xingchong, et al. Effect of state of movable support on elasto-plastic seismic response of bridges[J]. Journal of Highway and Transportation Research and Development, 2015, 32(3): 75−81.
[16] 王军文, 李建中, 范立础. 限位装置对连续梁桥地震反应的影响[J]. 铁道学报, 2008, 30(3): 71−77. WANG Junwen, LI Jianzhong, FAN Lichu. Effects of restrainers on seismic responses of continuous beam bridges[J]. Journal of the China Railway Society, 2008, 30(6): 71−77.
[17] 周云. 金属耗能减震结构设计[M]. 武汉: 武汉理工大学出版社, 2006. ZHOU Yun. Design of metallic energy dissipation damping structures[M]. Wuhan: Wuhan University of Technology Press, 2006.
Analysis of the influence of damping gap of the same spherical direction double spherical surface seismic mitigation and isolation bearing on seismic isolation performance
YU Weidong1, ZHANG Yongliang1, WU Yanwei2, WANG Xihui3
(1. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. China Railway Yiyuan Survey and Design Group Co., Ltd, Xi’an 710043, China;3. Hengshui Baoli Engineering Rubber Co., Ltd, Hengshui 053000, China)
In order to study the influence of longitudinal damping gap of the same spherical direction double spherical surface seismic mitigation and Isolation movable bearing on the seismic response of simply-supported beam bridge on high-speed railway, in this paper, a finite element model of double spherical bearings with the same spherical direction was proposed, considering the friction of bearings and the non-linearity of shock absorber dampers. The along-bridge nonlinear dynamic time-history analysis under rare earthquakes was carried out. The results show that simple supported beam bridge isolation system based on same spherical direction double spherical surface seismic mitigation and isolation bearings have the dual control effect of isolating seismic load and reducing the relative displacement of pier and beam. Appropriately reducing the damping gap of movable supports can greatly reduce the relative displacement of piers and beams without significantly increasing the bending moment at the bottom of piers. Properly adjusting the damping gap of the movable support can redistribute the energy consumption relationship between the components of the movable support itself, and optimize the energy consumption relationship between the fixed support and the movable support. The energy dissipation capacity of the movable bearing decreases with the increase of its damping gap.
high-speed railway; simply—supported beam bridge; the same spherical direction double spherical surface seismic mitigation and isolation bearing; seismic response; longitudinal damping gapof movable bearing
U448.13;U442.55
A
1672 − 7029(2019)09− 2240 − 08
10.19713/j.cnki.43−1423/u.2019.09.015
2018−11−28
中国铁建股份有限公司科研项目(15-C41);中铁第一勘察设计院集团有限公司科研(软件)开发项目(院科15-08)
张永亮(1975−),男,内蒙古通辽人,教授,博士,从事桥梁抗震理论研究;E−mail:zhangyong_L@126.com
(编辑 涂鹏)

