油品脱水用碟式离心机的流场及分离性能

张宇恒， 袁惠新， 付双成， 周龙远， 牟宇慧

(1.常州大学 机械工程学院，江苏 常州 213016； 2.江苏省绿色过程装备重点实验室， 江苏 常州 213016；3.波士顿大学， 马萨诸塞州 波士顿 02215； 4.江苏巨能机械有限公司， 江苏 宜兴 214261)

碟式离心机作为分离高度分散非均相混合物的重要分离设备，与工业其它分离设备相比，具有分离效率高、占地面积小，自动化程度高等优势[1-3]，广泛应用于化工、石油、食品、医药等行业。国外碟式离心机的技术参数范围较大，转鼓内径150～1200 mm，转速6000～12000 r/min，分离因数5000～15000，最大生产能力约300 m3/h。国内的碟式离心机产品系列少、规格少、技术参数低[4]，长期以来，碟式离心机的开发过程多是基于经验判断，严重影响了碟式离心机的发展和应用，与国际先进水平差距很大[5-8]。国内外对碟式离心机的研究主要是分析其动平衡、振动等问题，对设备分离性能的研究却很少。近几年国内学者对碟式离心机的研究与开发正日益增长，赵志国等[9-10]采用CFD技术对碟式离心机内部流场进行二维数值模拟，并对油滴的轨迹进行了追踪，初步分析了油-水分离形成的分层界面；张总等[11-12]基于FLUENT软件计算验证，提出高分离效果的碟片模型，并针对碟式分离机内流场流速进行了PIV测量。这些对离心流场的初步研究，均是基于二维模型的模拟，虽然减少了计算量，但是忽略了碟片结构、转速、物料特性等对流体流动的综合影响，必然导致模拟结果与实际流场有偏差，无法探究出碟式离心机分离效率的影响规律。袁惠新等[13-14]通过建立转鼓内简单三维物理模型，大致模拟出碟片间隙中微小区域的流动情况，但是研究中将碟片简化为光滑物理模型，没有考虑到碟片上筋条结构对碟片间物料流动性的影响。因此，笔者对碟式离心机内的流场及分离性能进行了系统的研究，综合考虑筋条结构对流体流动的影响，发现了碟片间物料存在旋转滞后性，且各层进料流量及重相体积浓度不一致性等现象。这些现象严重影响到碟式离心机的分离性能。

在一些特定条件下，航空煤油中往往稳定分布

极小粒度的水滴，当含水量大到一定程度，会严重影响航空发动机的性能[15]。因此，国际航空业对于航空煤油的含水量要求很高。这些水滴相对于其它固态杂质更难以分离，目前国内碟式离心机的工业技术水平尚无法实现航空煤油的油-水高精度分离。笔者主要通过碟式离心机内碟片上螺旋型与径向型筋条的对比研究，探讨了碟片上螺旋型筋条对碟片间两相流动及对航空煤油脱水性能的影响。

1 模拟研究方法及可靠性验证

1.1 碟式离心机转鼓模型

图1为碟式离心机转鼓结构。其主要是利用超重力沉降和浅池原理设计，即在离心沉降分离悬浮液时，其生产能力正比于沉降槽的面积，而与沉降槽的高度无关。其优势是利用碟片将分离室划分为若干分离区，用碟片来降低沉降高度，增加沉降面积，加速了离心沉降分离过程。

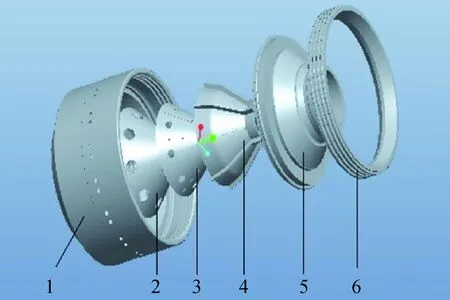
图1 碟式离心机转鼓三维爆炸视图Fig.1 3D explosion view of disc centrifuge drum1—Drum; 2—Disc holder; 3—Disc; 4—Disc gland;5—Drum cover; 6—Lock ring

1.2 物理模型及网格划分

笔者对碟式离心机采用CFD数值模拟，分离对象参考航空煤油。碟式离心机的主要结构参数及数值模拟中拟采用的物料参数和操作参数见表1。

表1 碟式离心机物理模型的模拟参数值Table 1 Simulation parameters of centrifuge physical model

由于碟式离心机内物料的离心沉降分离主要发生在碟片间隙，且碟片间隙内物料的沉降距离远远小于离心机转鼓半径，因此使用ANSYS 18.0前处理软件ICEM建立5层碟片间两相流动区域及转鼓成渣腔的三维流动模型，进料口与定距筋条作网格局部加密处理，以提高结构化网格质量。模型结构化网格如图2所示，其中图2(a)为传统带径向型筋条的碟片，图2(b)为笔者创新设计出的新型带螺旋型筋条的碟片。

图2 碟片间隙及转鼓成渣腔的三维流动模型Fig.2 3D flow model of disk gap and drum slag cavity(a) Radial rib; (b) Spiral rib

1.3 模型计算及边界条件

笔者研究碟式离心机碟片间两相流动场，由于无需考虑涡黏性各项同性假设，湍流模型比雷诺应力模型更加精准。在碟片间两相流动场中，物料受离心作用处于高速旋转运动。因此模拟中采用RSM湍流模型，其计算原理是质量守恒方程、动量守恒方程(Navier-Stokes，即N-S方程)、应力运输方程(Reynolds)[16-18]。模拟对转鼓内流场予以适当简化，并作以下假设：(1)转鼓内充满液体且流动稳定；(2)液相为连续不可压缩流体；(3)固相为密度均匀等粒径球形颗粒，且运动过程中不发生絮凝、破碎和变形。计算模型对两相间的相互作用，采取单流体计算方式，但计算模型中不仅包含了不同相间的相对运动，而且不同相间相对运动的速度大小不同，因此计算模型能够比较全面地分析碟片间两相流动过程。

入口边界条件采用速度进口(Velocity-inlet)，碟片上端出口设置采用压力出口(Pressure-outlet)；碟片下端出口设置与转鼓内流场相接，通过定义内部面观测碟片下端重相出口情况；流道内与流体接触的壁面均采用无滑移条件。

碟式离心机碟片间流场复杂，转鼓内流体旋转占优，因此通过RSM湍流模型模拟更加精准。碟片间两相流动属于多相流流动，采用Eulerian模型能够精准地研究碟片间两相流动性及其分离性能。

通过ANSYS 18.0进行数值模拟，采用压力-速度耦合方式(SIMPLE算法)、压力方式(PRESTO!格式)和其余项差(QUICK精度)。非稳态模拟流场在50000步后，出口监测面上的水相体积分数基本稳定，残差曲线也已经稳定，表明流场已经稳定。

1.4 模拟可靠性验证

针对实验物料航空煤油，采用DRS 230型碟式离心机进行实验(如图3)：(1)将物料装入进料罐中使物料通过并充满管路，通过离心泵灌泵口进行灌泵；(2)打开电源，启动碟片式离心机的同时启动离心泵(空载启动)，使物料在整个管路中循环；(3)调节变频器以调节入口流量及转鼓转速，待溢流稳定后取样；(4)采用浊度仪分析样品的浊度，通过标定的浊度和体积浓度，可得对应水相的体积分数。

当碟式离心机的转速n=3000 r/min，流量Q=1 m3/h时，离心机稳定后测得样品中油相的体积分数为99.2%，而通过数值模拟计算的体积分数为98.7%，模拟所得的体积分数比实验测得样品的体积分数低。这是因为在数值模拟中的粒径模型均为等粒径，油相的体积分数理论上不超过74%，而实际物料中的水相粒径大小不同，且水滴在油相中有聚合、破碎现象，因此在同样条件下，模拟得到的水滴体积分数自然会低一些。

2 碟片间两相流场分析

2.1 压力场

碟片间两相流场内离心液压的理论计算公式[19]为：

(1)

图3 碟式离心机实验流程图Fig.3 Dish centrifuge experiment flow chart

式(1)中p为离心液压，Pa；ρ为密度，g/mm3；ω为转速，r/min；r为径向位置，mm。由式(1)可知，离心液压与碟片间流场的径向位置成正比，与轴向位置无关，选取第3层碟片间流场压力云图作对比，结果如图4所示。由图4可知，流场内压力呈中心对称均匀分布，并且其值与径向位置成正比，由内向外逐步增大。模拟得到径向型筋条的碟片间两相流场在径向位置最大处(碟片大端)的压力最大值为1.46 MPa，在径向位置最小处(碟片小端)的压力最小值为0.12 MPa；螺旋型筋条的碟片间两相流场在径向位置最大处(碟片大端)的压力最大值为 1.49 MPa，在径向位置最小处(碟片小端)的压力最小值为0.12 MPa。

图5为碟片间两相流场内的离心液压理论值和模拟值。由图5可知，模拟值与理论值相差约8%，表明研究结果具有较好的可靠性。模拟结果表明，径向型筋条与螺旋型筋条在碟片间两相流场中的压力分布规律基本一致，但与离心液压理论值相比要小。这是因为流体靠近碟片表面流层的运动相对于碟片转速具有滞后性，碟片间两相流场内的转速(ω)比离心机转鼓转速小，因此碟式离心机碟片间两相流场内离心液压理论值一般大于实际流场。模拟研究还发现，新型螺旋型筋条与径向型筋条的碟片间两相流场压力相比，更接近于离心液压理论值，这说明新型螺旋型筋条能够较好地改善碟片间两相流场的滞后性。

图4 碟片间两相流场压力对比云图Fig.4 Comparison of cloud charts of disc pressure between the two phase flow fields(a) Radial rib; (b) Spiral rib

图5 离心液压理论值和模拟值Fig.5 Centrifugal hydraulic theoretical and analog values

2.2 速度场

物料在碟式离心机的碟片间两相流场做旋转运动，其离心力的大小与转鼓的转速成正比，碟片间两相流场内物料相对周向速度(v，m/s)的理论计算

公式为[20]：

(2)

式(2)中λ为无因次数；q为流量，m3/s；r为径向位置，m；h为碟片间隙，m。

由式(2)可知，碟片间流场周向速度与碟片轴向位置无关，取第3层碟片间流场周向速度云图作对比，结果如图6所示。由图6可知，碟片间两相流场内速度呈中心对称均匀分布，并且由内向外逐步增大。模拟得到径向型筋条的碟片间两相流场在径向位置最大处(碟片大端)的速度最大值为62.2 m/s，在径向位置最小处(碟片小端)的速度最小值为 24.5 m/s；螺旋型筋条的碟片间两相流场在径向位置最大处(碟片大端)的速度最大值为 62.2 m/s，在径向位置最小处(碟片小端)的速度最小值为23.2 m/s。

图6 碟片间周向速度云图Fig.6 Peripheral speed between disc clouds(a) Radial rib; (b) Spiral rib

图7是周向速度理论值(即碟片的周向速度)和模拟值。在碟片径向位置60 mm处物料的周向速度理论值为47.124 m/s，模拟值与理论值相差约1%，得以判断流场模拟具有较好的可靠性。模拟结果表明，径向型筋条与螺旋型筋条在碟片间两相流场中的周向速度分布规律基本一致，速度分布和一般的抛物线类似。由图7可知，螺旋型筋条的周向速度更接近于理论值，且近壁处达到最小值，碟片间隙中间区域达到最大值。这是因为当液流的无因次准数λ值大时，碟片间液流分成两层近壁处的液流，液体质点周向速度由近壁面向着碟片间隙的中心增加，在间隙中心处周向速度约为母线方向平均速度的λ-1 倍[21]，使碟片间隙内液流速度分布类似于一般的抛物线。

图7 周向速度随轴向位置变化的模拟值与理论值Fig.7 Analogue and theoretical values of circumferentialvelocity at different axial positions

2.3 两相分布

图8为第3层碟片间水相体积分数(φw)分布云图。由图8可知，在中性进料孔定距筋条附近有水相浓集现象。这是因为当物料由中性进料孔进入碟片间后，随着碟片旋转做离心旋转运动，而物料在碟片间的周向速度大，导致水相无法在中性进料孔及定距筋条附近流场区域均匀扩散，从而引起在中性进料孔附近区域水相体积分数偏高的现象。由图8还可知，带螺旋型筋条的碟片间，水相分布较为均匀，说明螺旋型筋条能够较好地改善碟片间水相分布的不均匀性。

图8 碟片间两相流场水相体积分数分布云图Fig.8 Volume fraction distribution cloud diagram of the two-phase flow field between discs(a) Radial rib; (b) Spiral rib

图9为x=0截面上各层碟片间两相流场内水相体积分数分布云图。由图9可知，碟片间两相流场内水相体积分数分布规律基本一致，碟片下表面水相体积分数高且与碟片径向位置呈正比。这是因为物料在碟式离心机转鼓内做离心旋转运动，水相受离心力的作用集中分布在碟片下表面，油相相对于水相流往碟片上端口，因此碟片间两相体积分数分布规律较为明显。但各层碟片间的水相体积分数不一，由图9可知，入料方向的第1层碟片间水相体积分数最高，因此对5层碟片中性进料孔做x=0的截面，即碟片进料孔及周边流动区域的水相体积分数分布云图，如图10所示。由图10可知，各层碟片间的水相体积分数不一，第1层与最后1层附近水相体积分数最高，中间层较少；水相体积分数自下往上递增，最上层的水相体积分数最高，油相体积分数最低。

图9 x=0截面上各层水相体积分数分布云图Fig.9 Distribution of volume fraction of water phase ineach layer at x=0 cross section

图10 进料孔及周边区域的水相体积分数分布云图Fig.10 Distribution curve of volume distribution ofwater phase in the feed hole and surrounding area

3 碟式离心机的分离性能分析

图11为各层碟片间两相中水相体积分数。由图11 可知，各层碟片间两相中水相体积分数分布不均，第1层与最后1层碟片间两相的水滴体积分数相对较大，径向型筋条在最后1层碟片间两相中水相体积分数最大，可达1.87×10-4；螺旋型筋条在第1层碟片间两相中水相体积分数最大，可达9.54×10-5。中间各层相对较小且分布不均，径向型筋条在第4层碟片间两相中水相体积分数最小，为5.11×10-5；螺旋型筋条在第4层碟片间两相中水相体积分数最小，为2.11×10-5。模拟结果表明，新型螺旋型筋条的各层碟片间水相体积分数，比径向型筋条要更小且分布更均匀，说明新型螺旋型筋条能够较好地改善各层碟片间两相的均匀性且水相体积分数更低，能够有效地提高碟式离心机的分离性能。

图11 各层碟片间水相体积分数Fig.11 Volume fraction of water between discs in each layer

4 结 论

(1)径向型筋条与螺旋型筋条在碟片间两相流场中的压力分布规律基本一致，压力值由碟片内端向外端逐步增大，模拟值与离心液压理论值相比要小，但很接近，说明模拟的可靠性较好。

(2)流体靠近碟片表面的流层运动相对于碟片转速具有滞后性，螺旋型筋条能够较好地改善碟片间流动的滞后性。

(3)同一径向位置上，液流的周向速度在平行于转轴的面内呈抛物线分布，近壁处达到最小值且贴近理论值，而在中间区域达到最大值。

(4)在碟片间两相流场内，螺旋型筋条比径向型筋条的周向速度要更贴近于理论值，螺旋型筋条能够较好地减小湍流，改善碟片间两相流场的稳定性。

(5)碟片间两相中水相的体积分数分布不均，其在中性进料孔、定距筋条附近较高，螺旋型筋条能够较好地改善碟片间水相体积分数分布的不均匀性。

(6)各层碟片间的水相体积分数不一致，第1层与最后1层碟片间的水相体积分数相对较大，中间各层相对较小且分布不均。螺旋型筋条能够较好地改善各层碟片间两相均匀性且水相体积分数更低，能够有效地提高碟式离心机的分离性能。