V形拱梁拱组合桥成桥索力的确定

王 佩 周 麟 张振伟

(1.武汉工程大学土木工程与建筑学院，湖北 武汉 430073; 2.上海林同炎李国豪土建工程咨询有限公司湖北分公司，湖北 武汉 430050)

V形拱梁拱组合桥造型美观，具有良好的美学效果。随着科技发展，梁拱组合桥的造型越来越复杂多样，而结构异化所引起的结构复杂、施工困难等问题也引起了越来越多学者与专家的重视。V形拱梁拱组合桥设计中拉索初张拉力是影响桥梁成桥状态的重要参数，是保证桥梁合理成桥状态的基础。

V形拱梁拱组合桥依靠拉索将桥面荷载传递给拱肋，主拱肋通过拉索与主梁连接成一个整体，以达到桥梁结构受力的自平衡。拉索张拉是相关桥梁关键施工步骤之一，拉索张拉的问题主要有两个[1]：一是如何确定拉索在各阶段索力的目标值，二是确保每根拉索张拉力达到目标值。如何方便快捷的确定合理成桥状态及各施工阶段拉索的张拉力值并对成桥后索力的调整就成为问题的关键和重点[2]，只有合理的确定才能保证施工期安全，使成桥状态与设计相符。

拉索拱桥在设计施工过程中，基于合理成桥状态下拉索初拉力的确定，常用方法有：刚性支撑连续梁法、力的平衡、能量弯曲最小法、零位移法[3，4]，本文以海兰湖V形拱梁拱组合桥为背景，采用刚性支撑连续梁法对V形拱桥的拉索初张拉力进行分析，并对刚性支撑连续梁法中拉索松弛问题提出相应的解决办法。

1 刚性支撑连续梁法计算原理

刚性支撑连续梁法即求一组拉索初张拉力，使主梁与拉索连接处节点在恒载作用下一次成桥状态下的位移为0，并且同时认为主梁内的弯矩为刚性支撑连续梁弯矩[5]。因此，确定桥梁的合理成桥状态，主要是以桥梁斜拉索的初始张拉力为控制因素，以拉索与主梁连接处的节点的位移为控制目标。

根据施工步骤中一次落架成桥方式，计算桥梁在不施加拉索初始张拉力时，仅在恒载作用下主梁与拉索连接处节点的竖向位移Δ。然后依次算出单根拉索在单位荷载作用下各节点位移的影响向量δij，i为主梁与拉索的节点编号，j为桥梁拉索编号，单位荷载作用的影响矩阵[A]，以节点位移为0，写出线性方程如下：

[A]{T}+{Δ}=0

(1)

其中,{T}={T1,T2,T3,…,Tn}T,Ti为第i根拉索初始张拉力;{Δ}={Δ1,Δ2,Δ3,…,Δn}T，Δi为第i根拉索在恒荷载单独作用下与主梁连接处节点竖向位移。

(2)

于是可以得到：

(3)

利用式(3)可得到桥梁合理成桥状态时，满足拉索与主梁连接处节点位移为0的拉索初张拉力。

2 海兰湖大桥拉索初张拉力计算

2.1 工程概况

海兰湖大桥造型独特，属于V形拱梁拱组合桥。与一般竖向二维空间拉索拱桥相比，该桥梁拉索处于三维空间中，使得桥梁受力及变形更复杂，因此采用一种目标明确，概念清晰的确定拉索初张拉力的计算方法至关重要。海兰湖大桥构造上为钢构梁拱组合桥，跨径布置为(90+115+30)m。主桥跨度115 m，主桥上部两侧分别设两片钢拱肋，采用六边形截面拱，主桥示意图见图1。拱肋平面内形成17.6°的夹角呈V形，外倾的主拱圈利用拉索承受主梁的荷载。分别设置8对拱拉索，拉索水平间距8 m，拉索布置图见图2。

2.2 计算模型

根据该桥梁的结构特点，应用Midas/civil有限元分析软件，建立桥梁上部结构有限元模型，初张拉力以体外力方式添加，确保

张拉后拉索力的确定性[6]。主梁采用钢箱梁断面，拱肋采用六边形钢拱，拱截面拱顶高2.0 m，拱底高2.5 m，为主要受力结构；拉索采用桁架单元，其他结构采用梁单元，计算模型中共建立桁架单元32个，梁单元449个，如图3所示。

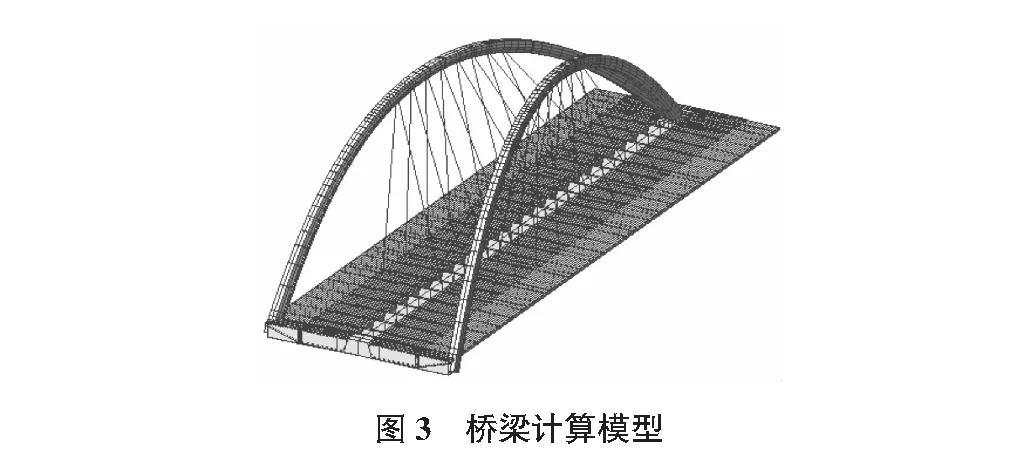
2.3 计算结果及分析

利用Midas/civil计算得出影响矩阵[A]。两侧各8对拉索为非对称结构，故需要对32根拉索进行计算。对每根拉索施加单位荷载，求解出拉索与主梁连接处节点的位移影响矩阵。得出影响矩阵如下：

恒荷载单独作用下各目标节点位移Δi的计算结果见表1。

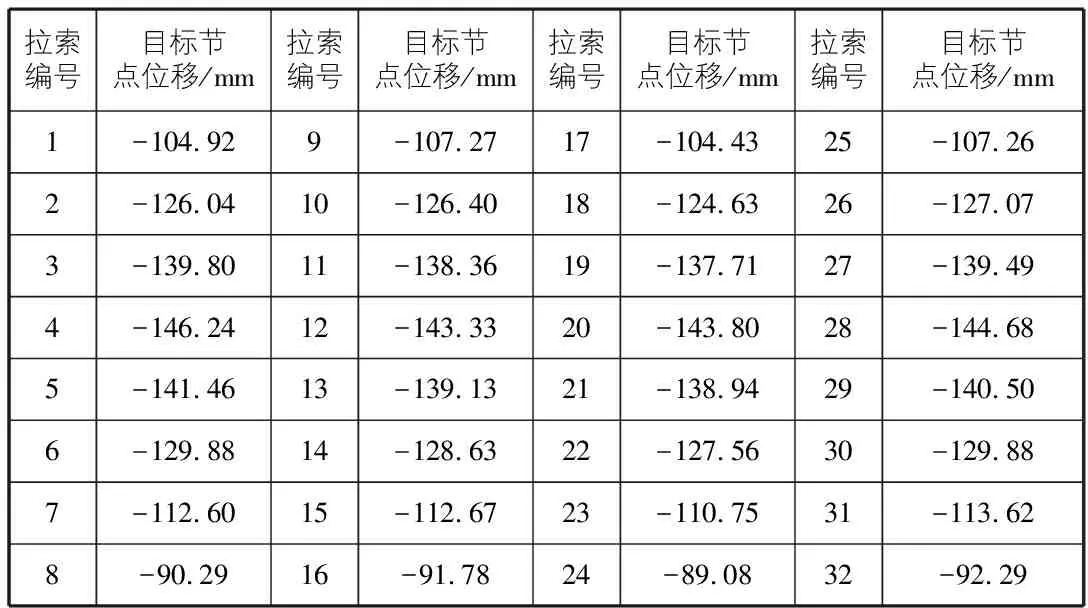
表1 恒荷载作用下目标节点位移

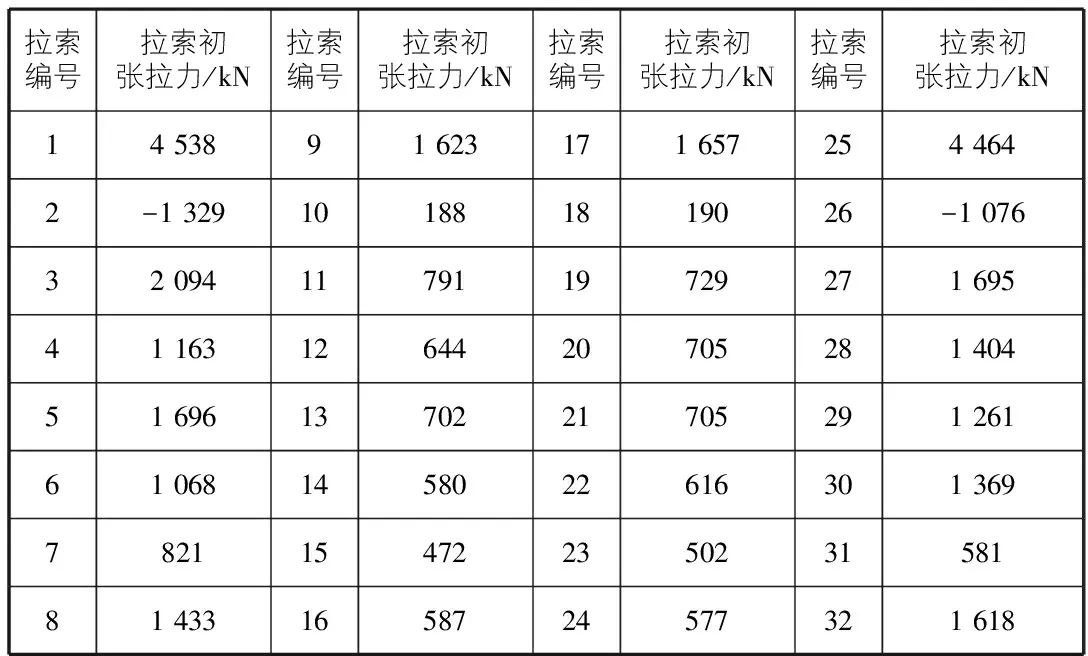
表2 拉索初张拉力Ti

将以上所得矩阵[A]及{Δ}代入式(3)求得最终拉索初始拉力Ti，计算结果见表2。表2中计算结果显示，刚性支撑连续梁法所得计算结果不均匀，且出现拉索松弛现象，因此为保证全部拉索处于紧绷态而受拉，需对拉索初拉力进行调整。

2.4 拉索初拉力的调整

表3 恒载单独作用下拉索内力表

表4 调整后拉索初张拉力Tk及对应控制节点位移

成桥后拉索张拉力的目标控制值理论上保证了拉索与主梁连接处节点位移为0，但是要考虑到拉索不能出现松弛现象，同时考虑成桥后结构线形变化，对表2中拉索初张拉力进行调整。按照主梁在拉索拉力的作用下保持平衡的原理，考虑成桥后结构的线形变化，对应恒荷载单独作用下产生的拉索内力值，单根拉索的内力值占所有拉索总内力值的比例对表2中拉索初张拉力按相同趋势下等比例原则进行对应的调整，见式(4)。仅在恒载作用下拉索所受内力值如表3所示。

(4)

其中，Tk为调整后的拉索拉力；Ti为表2中对应的拉索拉力；Tj为恒荷载单独作用下产生的拉索内力值。

规范规定跨度为L的桥梁纵向最大允许位移为L/500，将初次调整后的拉索拉力导入有限元模型对其进行相应的微调，调整后拉索初张拉力Tk计算结果及对应控制目标节点位移如表4所示。

表4调整后拉索初张拉力及节点位移显示，由于端部1号、9号、17号、25号拉索距梁端28 m，间距较大，处于无拉索区，导致端部节点竖向位移相对较大，但调整后目标节点位移均小于最大允许位移的5%，从而得出，以拉索与主梁连接处节点竖向位移为0为控制目标，控制桥梁在恒载作用下的竖向位移，以刚性支撑连续梁法，计算结果出现拉索松弛时，按照恒载作用下的拉索受力趋势，保证主梁结构的线性变化，调整拉索初张拉力。与恒载单独作用下的竖向位移比较，调整后主梁与拉索连接处节点位移较小，满足规范要求。

3 结语

V形拱梁拱组合桥受力复杂，利用刚性支撑连续梁法计算初张拉力，得到拉索张拉力，方法概念清晰，计算简单，并在利用刚性支撑连续梁法计算时拉索出现松弛的情形下提出基于成桥恒荷载作用下拉索受力特性等比例原则，调整拉索初拉力，使计算结果在保证成桥状态下更符合工程实际，在设计工作中得到应用。